AP325
跨出精進演算法的第一步
洪翠憶
Index
AP325連結

AP325 Introduction
〞
程設資結迷惘,算法遞迴如夢,冷月豈可葬編程,柳絮靜待東風。
鄭愁予:「我打江南走過,那等在季節裏的容顏如蓮花的開落,東風不來,三月的柳絮不飛,你的心如小小寂寞的城,...」直到遇上了程式,......。
– 吳邦一 教授
AP325簡略目錄
AP325簡略目錄
AP325簡略目錄
AP325簡略目錄
AP325簡略目錄
2-1班群可能會學到的部分
教材說明
- AP325 → APCS 實作3級分 to 5級分
- 實作考4題,每題100分
- 實作題難度幾乎都是由簡單排到難
- 三級分的程度大概是會做好前兩題,五級分只能錯半題,要達到四五級就是要答對第三第四題
- 第三與第四題則涉及常見的資料結構與演算法
- APCS的編譯環境: C++版本為 C++ 11、編譯器優化為 O2...
- 針對考試與競賽的

競賽版
C++起手式
#include <bits/stdc++.h>
//萬用標頭檔
using namespace std;
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
//優化cin/cout速度
// code here
return 0;
}-
𝐜𝐢𝐧/𝐜𝐨𝐮𝐭效率不佳,容易TLE(time limit exceed,執行超過時限),習慣用𝐬𝐜𝐚𝐧𝐟/𝐩𝐫𝐢𝐧𝐭𝐟的話就不會有這個問題

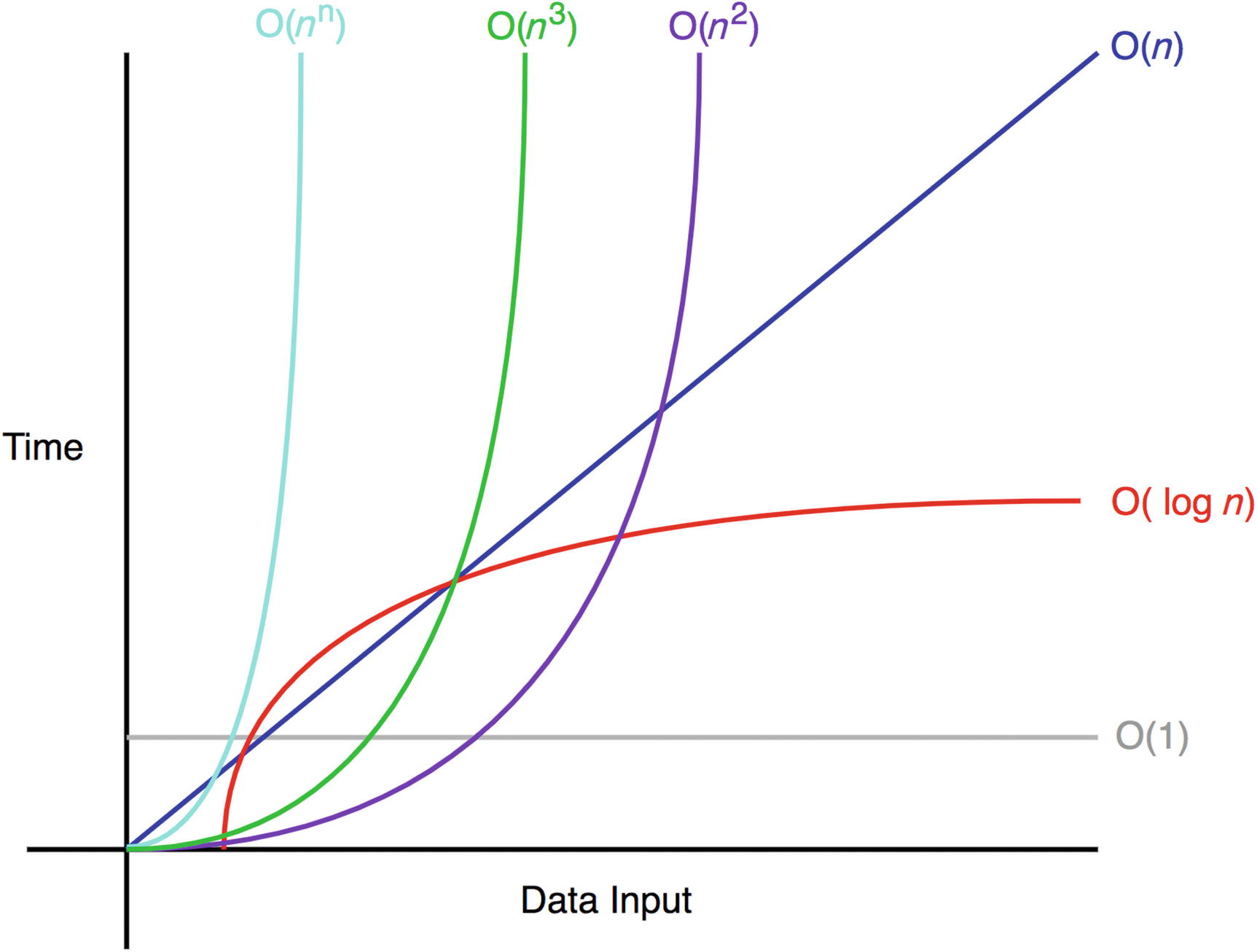
Big O
表示法:O(𝐟(𝐧))
- n: 資料量
- 意義:當資料量為 n 時,這個程式(演算法)的執行時間(執行指令數)不超過 f(n)的某個常數倍
- 資料量大小:輸入的資料量,例如整數個數、字串長度等等
- 常見的複雜度有:O(n)、O(n*log(n))、O(n^2)、O(2^n)...
原則
-
根據定義,不計算常數倍數
- 沒管O(2n)、O(4n)那些
- 所以log(n)不必指明底是2或10
-
兩函數相加時算比較大的那個
- 若O(f(n)+g(n)),其中f(n)>g(n),則會表示成O(f(n))
-
若O(𝐟(𝐧))執行𝐠(𝐧)次,則O(𝐟(𝐧)*𝐠(𝐧))
-
一般的複雜度指的是worst-case複雜
- 最難計算的資料所需的時間
- 程式的複雜度通常會因為輸入資料不同而改變
舉例
char a[100];
std::cin >> a;
std::cout << a;O(1)
int n;
char a[100];
std::cin >> n >> a;
for(int i = 0; i < n; i++)
std::cout << a[i];O(𝐧)
int a = 2, arr[5] = {2, 5, 7, 9, 25};
int s = 0, e = 4, i;
do{
i = (e + s) / 2;
if(arr[i] == a){
std::cout << "find it at " << i << ".\n";
break;
}else if(arr[i] > a)
e = i;
else
s = i;
}while(e - s > 0);
std::cout << "end";O(𝐥𝐨𝐠(𝐧))

需要留意的事
整數溢位(Overflow)
-
成因
- 變數若超過型態可表示範圍,就會發生溢位
- 編譯器無法察覺
-
解決方法
- 一律用long long存整數(int只能存4 bytes,但long long可存8 bytes)
- 取模數(modulus)
%
10
15
5
int用C語法轉型long long & 簡單講一下位元運算
long long a = 1 << 40;
//1和40會被當成int,所以在回傳到a時它還是個int,故溢位
long long a = (long long)1 << 40;
//C風格轉型-
<<:左移運算子
-
>>:右移運算子
ex.
1 << 4 = 16
00001 << 4 = 10000
判斷式的短路求值(short-circuit evaluation) & 編譯器優化
while(i < 5 && a[i] != 0)
//&&若前面條件已不符合,則直接回傳false
for(int i = 0, len = a.size(); i < len; i++)
//這樣就不用每跑一次迴圈,取一次大小了
Kahoot!

Reference
Introduction of ap325
By justhentai
Introduction of ap325
- 503



