C++與演算法

by 建國中學賴昭勳張均豪

C 與 C++ 介紹

程式語言...?

人類和電腦溝通的工具
一個功能多很多的計算機（？
高階 v.s. 低階語言
人工智慧、遊戲製作、網頁處理...

那C跟C++又是什麼？

C 語言是最早研發出來的高階（使用者友善）語言之一

C++ 是建立在C語言之上，對許多語法和功能進行改良，增加了標準函式庫，是目前競賽程式最常使用的語言

編譯與執行

編譯：電腦（編譯器）將程式碼自動翻譯變成組合語言（電腦看得懂的指令）。

執行：將編譯後的程式使用。

開發環境介紹

Codeblocks!

優點：常見，比賽會有

缺點：很容易爛掉，mac 沒有

Dev C++

優點：常見，比賽會有

缺點：很容易爛掉，mac 沒有

之後的活動

HPC, NPSC, APCS, 資芽

APCS

aka 後測大賽&&爛筆試

NPSC

aka 建中被debuff的神奇團體比賽

HP Codewars

aka Cosplay + 吃東西(今年沒有）歡樂賽

資芽

aka 認識隱藏版電神+國手電神課程

分成語法班 and 算法班
在台大資工系上課（酷
要寫作業www

YTP

aka 爽領一萬八的比賽

ISSC

aka 可以出國的神奇比賽

Hello, World!

#include <iostream>
using namespace std;
int main() {
	cout << "Hello World!" << endl;
}

C++ 程式的組成

1. 標頭檔

用來使用某些特定的內建功能，引入內建的函式庫。
基本上寫在最前面
處理C++式輸入輸出：#include <iostream>

2. 命名空間

程式裡面的一組物件、類別、函式加上的標籤（為了避免名稱相撞）
標準函式庫：using namespace std

許多功能原本需要加上 std::function_name

using 就是直接告訴編譯器：「跟std名字一樣的東西就是std的」

3. 主函式

C++ 程式執行時會自動跑的函式
int main() {}

回傳值：給編譯器看

名字跟參數

程式碼放這

\注意/

#include <iostream>
using namespace std;
int main() {

}

#include <iostream>
using namespace std;
int main() 
{

}

唯一真理

邪教

自己試試看吧！

資料型別與變數

C++ 如何儲存資料

不是01010111嗎？

雖然電腦裡所有資料都是二進位，程式語言會為使用者做好資料型別（data types），以方便處理不同種類的資料.

名稱	大小（位元組）	數值範圍
int	4	-2147483648~2147483647
unsigned int	4	0~4294967295
long long	8	-2^63~2^63 - 1
char	1	-128~127 (或0~255)
float	4	3.4E +/- 38 (7 位數)
double	8	1.7E +/- 308 (15 位數)
long double	8 (?)	1.7E +/- 308 (15 位數)
bool	1	true 或 false

常見資料型別（不用全背）

變數

儲存資料的地方

int a;

型別

名稱

可以想成「記憶體中的某個放東西的位置」

有了變數可以做什麼？

運算子(operator)

對資料進行某種操作和改變
每個型別能用的運算子和功能不太一樣

int 的運算子

名稱	功能
賦值(=)	將左邊的變數數值改成右邊的
加(+)	略
減(-)	略
乘(*)	略
除(/)	會自動取下高斯喔
模運算(%)	a % b 為 a 除 b 的餘數

實作練習：

在程式裡面輸入兩個數字，輸出他們相加後的平方

int main() {
    int a = 5, b = 5;
    cout << ????? << endl;
    //此處 ? 應為 100
}

每次進去程式改太麻煩了！

用輸入函式跟終端機互動！

int main() {
    int a;
    cin >> a;
    char c;
    cin >> c;
    int x, y, z;
    cin >> x >> y >> z;
}

實作time

把剛剛的程式修改成可以輸入的

條件判斷

如果...那麼...

布林值是啥？

一個可以存取「是」或「否」的型別
是：正確的，否：錯誤的

ex. 寫程式要多練習->true

大括號換行是好事->false

如果...那麼...

控制哪一些程式被執行！

if (條件成立) {
    //執行程式
}

裡面的條件其實就是一個布林值！

關係運算子

== (不是表情符號）

int a = 7122, b = 7122;
if (a == b) {
    cout << "same" << endl;
}
if (a != b) {
    cout << "not same" << endl;
}

== 會判斷兩邊的東西是否相同

!= 會判斷兩邊的東西是否不相同

其他關係運算子

名稱	功能	舉例
!=	判斷兩者是否不同	5 != 8
<	左<右	7 < 9
<=	左<=右	-5 <= -5
>	左>右	6 > 4
>=	左>=右	8 >= 8

回到剛剛的程式

不覺得有點冗嗎

int a = 7122, b = 7122;
if (a == b) {
    cout << "same" << endl;
}
if (a != b) {
    cout << "not same" << endl;
}

顯然，要不然就\(a\)跟\(b\)一樣，要不然就不一樣，幹嘛寫兩次？

如果...否則

int a = 7122, b = 7122;
if (a == b) {
    cout << "same" << endl;
}else {
    cout << "not same" << endl;
}

顯然，要不然就\(a\)跟\(b\)一樣，要不然就不一樣，幹嘛寫兩次？

現在，來點更複雜的

int a = 7122, b = 7122;
if (a == b) {
    if (a == 7122) {
        cout << "INFOR" << endl;
    } else {
        cout << "same" << endl;
    }
}else {
    cout << "not same" << endl;
}

假設我有兩個條件要同時判斷呢？

（\(a == b\) 且 \(a == 7122\))

可以寫兩次 if !

布林值之間的運算子

名稱	白話文	舉例
and (&&)	左右都對	true && true == true, false && true == false
or (\|\|)	其中一個對	true \|\| false = true, false \|\| false = false
not (!)	對變錯，錯變對	!true = false, !false = true
xor (^)	左右不相同	true ^ false = true, true ^ true = false

把兩個條件看成布林值來做運算

布林值之間的運算子

int a = 7122, b = 7122;
if (a == b && a == 7122) {
    cout << "INFOR" << endl;
}
if (a == b) {
    cout << "same" << endl;
}else {
    cout << "not same" << endl;
}

還可不可以更精簡一點？

如果...否則如果...否則

int a = 7122, b = 7122;
if (a == b && a == 7122) {
    cout << "INFOR" << endl;
} else if (a == b) {
    cout << "same" << endl;
} else {
    cout << "not same" << endl;
}

if 加在開頭
else if 加在中間（幾個都可以）
else 加在最後

練習時間！

奇偶性判斷

http://www.tcgs.tc.edu.tw:1218/ShowProblem?problemid=a012

Hint: 還記得剛剛講運算子的時候有一個東西叫做取模 (%) 嗎？

閏年判斷

http://www.tcgs.tc.edu.tw:1218/ShowProblem?problemid=a016

仔細看條件吧！

最後一題！

輸入兩個數字\(a, b\)

如果a, b都是 7122就輸出"INFOR"
如果a, b都不是7122就輸出"BAD"

邏輯大挑戰？！

	a == 7122	a != 7122
b == 7122	GOOD	X
b != 7122	X	BAD

int main() {
    int a, b;
    cin >> a >> b;
    if (a == 7122 && b == 7122) {
        cout << "GOOD" << endl;
    }
    if (a != 7122 && b != 7122) {
        cout << "BAD" << endl;
    }
}

迴圈

有一些東西要重複很多次，甚至不知道要做幾次，怎麼辦？

用迴圈!!!

while 迴圈

while (條件成立) {
    //做事
}

飯粒

int a = 5;
while (a > 0) {
    cout << a << endl;
    a = a - 1;
}

while 的使用時機

要重複執行東西的時候(廢話)
不知道要重複執行幾次的時候

while 例題: 去除偶因數

輸入一個正整數\(n\)，當那個整數還是偶數的時候，將他除以2，除到不能再除，最後輸出\(n\)

ex:\( n = 28, \ 28 / 2 = 14, \ 14 / 2 = 7\)

for 迴圈

有點像是while 的進階版!

不覺得有時候只要重複幾次怎麼辦?

與髮

for (起始條件; 判斷條件; 更新動作) {
	//做事
}

舉個例子吧!

for (int i = 0;i < 10;i++) {
	cout << i * i << endl;
}
/*
輸出
1
4
9
16
25
36
49
64
81
100
*/

重複變數次數

int n;
cin >> n;
for (int i = 0;i < n;i++) {
	cout << i * i << endl;
}
/*
輸出
1
4
9
16
...
n^2
*/

練習：

輸入一個整數，輸出那個整數以下（包含自己）所有5的倍數（從5 開始算5, 10, 15）

ex: 輸入 13，輸出5, 10

輸入20，輸出5, 10, 15, 20

練習：

輸入一個整數，判斷該數字是不是完全平方數。

是的話輸出YES，否則輸出NO

ex: 輸入 13，輸出NO

輸入25，輸出YES

解答：5的倍數

#include <iostream>
using namespace std;
int main() {
	int n;
	cin >> n;
	for (int i = 1;5 * i <= n;i++) {
		cout << 5 * i << endl;
	}
}

解答：完全平方數

#include <iostream>
using namespace std;
int main() {
	int n;
	cin >> n;
	int ans = 0;
	for (int i = 1;i <= n;i++) {
		if (i * i == n) {
			ans = 1;
		}
	}
	if (ans == 1) {
		cout << "YES" << endl;
	} else {
		cout << "NO" << endl;
	}
}

剛剛的程式是不是多跑了很多？

如果我想要有解就跳掉怎麼辦？

#include <iostream>
using namespace std;
int main() {
	int n;
	cin >> n;
	int ans = 0;
	for (int i = 1;i <= n;i++) {
		if (i * i == n) {
			ans = 1;
		}
	}
	if (ans == 1) {
		cout << "YES" << endl;
	} else {
		cout << "NO" << endl;
	}
}

break

把 for迴圈提前退出！

#include <iostream>
using namespace std;
int main() {
	int n;
	cin >> n;
	int ans = 0;
	for (int i = 1;i <= n;i++) {
		if (i * i == n) {
			ans = 1;
			break;
		}
	}
	if (ans == 1) {
		cout << "YES" << endl;
	} else {
		cout << "NO" << endl;
	}
}

continue

如果你要寫 if，懶得寫else 的時候

#include <iostream>
using namespace std;
int main() {
    int tens = 0;
    for (int i = 0;i <= 100;i++) {
    	if (i % 10 != 0) {
        	continue;
        }
        tens++;
    }
}

for 迴圈疊for 迴圈...

大家要記得，上面寫的這些東西都可以重複堆疊喔!

for (int i = 0;i < 10;i++) {
	for (int j = 0;j < 10;j++) {
    	cout << i * 10 + j << endl;
    }
}

再看一個東西

#include <iostream>
using namespace std;
int main() {
	for (int i = 1;i <= 5;i++) {
		for (int j = 1;j <= i;j++) {
			cout << j << " ";
		}
		cout << endl;
	}
}

會輸出什麼呢？

現在，你已經會寫基本的程式了!

Q1: 輸入一個整數，判斷該數字是不是質數。如果是的輸出 YES, 否則輸出 NO

實作囉!

Q2: 3N + 1問題

輸入一個整數，之後按照以下規則改變他:

如果他目前是偶數，將他除以 2

如果他是奇數，將他乘以3之後加上1

重複執行直到該整數變成1，並列印出過程

ex(26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1)

Q3: ZJ 的怪題qwq

https://zerojudge.tw/ShowProblem?problemid=a005

已知數列的前四項，填出第五項。

已經知道這些數列只可能是等差或等比數列。

(數列的前五項均為不大於105的自然數，等比數列的比值也是自然數)

ex. 1, 3, 5, 7 --> 9

1, 2, 4, 8 --> 16

陣列

陣列是啥

int arr[4]={7,1,2,2};

arr[0]	arr[1]	arr[2]	arr[3]
7	1	2	2

記得是從零開始算

int arr[4]={7,1,2,2};
arr[3]=5;
for(int i=0;i<4;i++){
    cout<<arr[i]<<" ";
}
//7 1 2 5

int n, arr[10];
cin>>n;
for(int i=0;i<n;i++){
    cin>>arr[i];
}

小提醒

陣列大小要是個常數，不能是變數

雖然新版C++好像開放可以用了

不過還是不要用比較好

還有如果陣列開過大(\(10^5\)以上)

可以開全域(main函數外面)

比較不會爆記憶體，而且可以不用初始化

二維陣列

你有一些陣列，這些陣列排成一個陣列

於是，你就得到了二維陣列

1	2	3
4	5	6
7	8	9

int arr[3][3]
={{1,2,3},
  {4,5,6},
  {7,8,9}};

int n, m, arr[10][10];
cin>>n>>m;
for(int i=0;i<n;i++){
    for(int j=0;j<m;j++){
        arr[i][j]=i-j;
    }
}
for(int i=0;i<n;i++){
    for(int j=0;j<m;j++){
        cout<<arr[i][j]<<" ";
    }
    cout<<"\n";
}

0	-1	-2	-3	-4
1	0	-1	-2	-3
2	1	0	-1	-2
3	2	1	0	-1
4	3	2	1	0

高維陣列?

你有一些二維陣列，這些二維陣列排成一個陣列

於是，你就得到了三維陣列

繼續下去還可以得到四維、五維...n維陣列

不過維度也不用太多，夠用就好

陣列真好用

題目中跟序列有關的東西都可以用陣列儲存

然後再搭配前面的迴圈、if/else，

就可以解決很多基礎題目。

實作時間

Q1:GreenJudge上的簡單題

http://www.tcgs.tc.edu.tw:1218/ShowProblem?problemid=b004

給定\(N\)、\(M\)以及長度為\(M\)的序列\(A\)，

請輸出\(1\)~\(N\)中有哪些數字沒在\(A\)中出現

實作時間

https://zerojudge.tw/ShowProblem?problemid=a015

Q2:ZeroJudge上的簡單題

輸入一個矩陣，輸出其翻轉的結果

實作時間

https://codeforces.com/problemset/problem/1433/B

Q3:Codeforces上的簡單題

給定一個只有0或1的序列，每次可以將一段連續的1往左或右移一格，求最少需要幾次操作才能使所有1合併成連續的區間

實作時間

Q4: Bubble Sort

給定一個長度為\(N\)正整數序列，將其由小到大排序

想法: 從左到右依序考慮每對相鄰的數，

如果左邊比右邊大就交換，

於是最大的一定會到最右邊，

所以重複\(N\)次就做完了。

要跑多久?

演算法入門

複雜度分析，二分搜技巧

複雜度分析

這個程式要跑多久？

0.3 秒
\(8*10^7\) 個基本運算
\(O(n \log n)\)

這些表示方法有哪些優缺點呢？

如果問題的大小不固定要怎麼解釋程式的效率？

複雜度分析

（時間）複雜度：一個演算法的計算時間與

問題大小的函數關係

通常以\(O(g(n))\)表示

程式執行時間：

問題大小 \(\times\) 時間複雜度 \(\times\) 運算次數的常數 \(\times\) 單位運算時間

來個範例：找出陣列中最大的數字

程式執行時間：

問題大小 \(\times\) 時間複雜度 \(\times\) 運算次數的常數 \(\times\) 單位運算時間

問題大小： \(10^6\)個數字
時間複雜度： \(O(n)\) ，計算量和問題大小成線性關係
運算次數： \(x\) 次 (包含輸入、儲存變數、比較數字）
單位運算時間：電腦一秒可以執行 \(3 * 10^8\) 個基本運算（加減、賦值...）

不同時間複雜度的差異

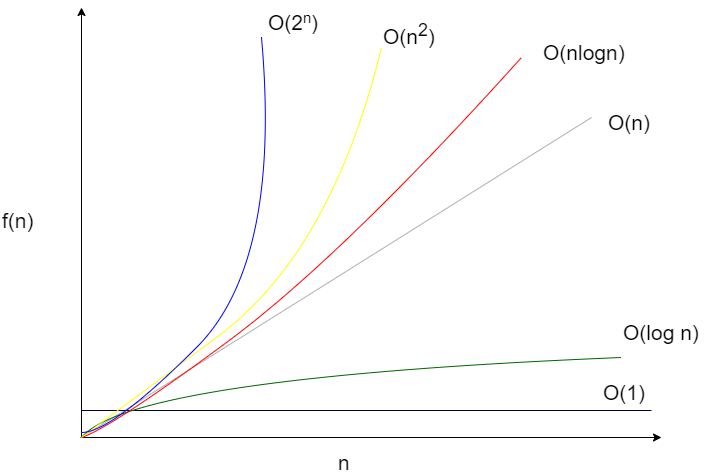
對於一個比較大的複雜度

只要問題大小（n）夠大，計算量一定比複雜度小的還多！

階乘 > 指數 > 多項式（次方越大就越大）> 對數 > 常數\(O(1)\)

時間複雜度的表示方式

沒有常數項（\(O(300*n)\) 還是算\(O(n)\))
有很多項的時候取最大的那一項（比較方式上一頁有寫）
有多個變數的時候分開標註 ex. \(O(n + q \log n)\)

要怎麼算程式的時間複雜度？

看 for, while 迴圈跑的範圍，估計每一個迴圈會被執行幾次（相對於 n 而言）
分開的 for 迴圈的時間相加，只要看跑得比較久的就好了
巢狀（for 迴圈在 for 迴圈）迴圈的複雜度要相乘。

還有期望複雜度、均攤複雜度（課外）....

int n;
cin >> n;
for (int i = 0;i < n;i++) {
    for (int j = 0;j < i;j++) {
    	cout << 7122;
    }
}

int n;
cin >> n;
for (int i = 2;i <= n;i++) {
    for (int j = 2;j * j <= n;j++) {
    	cout << 7122;
    }
}

以下這些程式的複雜度是多少呢？

\(O(n^2)\)

\(O(n \sqrt{n})\)

int n;
cin >> n;

int cnt = 0;
while (n > 0) {
    cnt++;
    n /= 2;
}
cout << cnt << endl;

int n;
cin >> n;
for (int i = 1;i <= n;i++) {
    for (int j = i;j <= n;j += i) {
    	cout << j << endl;
    }
}

以下這些程式的複雜度是多少呢？pt.2

\(O(\log n)\)

\(O(n\log n)\)

來玩個遊戲

現在我心裡想一個 \(1\)~\(10000\)的數字，你每次可以猜一個數字，而我會告訴你是命亻中，太大還是太小。你們能在幾次之內猜到呢？

能不能設計一種方法讓你猜的次數平均最少?

從之前的資訊可以得到答案可能的範圍!

當這個範圍的大小只有 1 (只剩一個數字可能是答案)你就一定猜的到!

那要怎麼讓範圍快一點縮小?

二分搜尋法

從這裡切的話，不管怎麼樣範圍都會小一半

平均下來只要切 \(O(\log n)\)次!

實作技巧

#include <iostream>
using namespace std;
int main() {
    int n;
    cin >> n; // number from 1~n
    int low = 1, up = n + 1, mid;
    while (up > low) { //[low, up)
        mid = (low + up) / 2;
        cout << "Is " << mid << " bigger (0), smaller (1), or equal (2) to answer?" << endl;
        int res;
        cin >> res;
        if (res == 0) {
            up = mid;
        } else if (res == 1) {
            low = mid + 1;
        } else {
            cout << "The answer is " << mid << endl;
            break;
        }
    }

}

二分搜好像沒有很難嗎?

來看看他的一些應用...

Green Judge h098

田忌賽馬

http://www.tcgs.tc.edu.tw:1218/ShowProblem?problemid=h098

等等，這跟二分搜有什麼關係

單調性是甚麼?

回想剛剛猜數字的邏輯

把每次詢問的回答變成小於或不小於兩種
對於詢問的回答可能會長這樣

比他小的

不比他小的

而這個判斷條件可以換成任何一個布林值!

可以做到 v.s. 不能做到

大於答案 v.s. 小於答案

回到田忌賽馬

可以知道:如果我等越多天，贏的可能就會越大

那再用剛剛的圖示

贏不了

贏得了

也就是說，如果我能夠知道過了某個天數能不能贏，我就可以快速(\(O(\log C)\)) 次知道這個分界點!

那要怎麼檢查可不可以

把每一隻馬在 \(x\)天之後的威力由大到小排序。

可以證明，如果我把最大的對上第 \(k\)小的馬，第二大對上第\(k - 1\)小，以此類推。這樣的策略會最好。(proof is left as an exercise for the readers)

那他的複雜度會是 \(O(n\log n)\)檢查

總複雜度 \(O(n \log^2 n)\) 喔!(死

喔耶再一題

給定一個數線上的\(N\)個點，求在數線上選取\(K\)個點時，被選取的點兩兩之間的距離最大可以是多少。

\(k \leq N \leq 10^5\)

感覺沒有一個好的選法

通常二分搜的題目會長這樣: 找到最大(最小) 的數字，使得他符合(不符合)某種條件。

觀察看看他的單調性!

思考流程

如果我們看答案，那我們要求的答案越小，越有可能會可以選到 \(k\)個東西!

那要怎麼檢查能不能放 \(k\) 個東西呢?

最後一題

數線上有 \(n\)個郵筒，每個點座標\(a_i\)，你有\(k\)個郵差，每個郵差至多可以負責 \(m\)個郵筒。定義一個郵差的「投遞範圍」為（他負責最右邊的郵筒 - 最左邊的郵筒）。在這些限制下，所有郵差投遞範圍最大值最小可以是多少？

ex. (A -> 1, 3，B -> 5, 7, 8，C -> 9

答案為\(\max(3 - 1, 8 - 5, 9 - 9) = 3\))

一樣的流程

有單調性嗎？

怎麼檢查答案？

答案越大，越有可能分好所有的郵差

先選前面的，紀錄目前選的個數。只要個數超過\(m\)或者距離超過限制，就是不可能達到

注意事項

mid必須要可以跑到所有需要的範圍 [答案可能最小值~答案可能最大值]
記得在 c++ 的除法是無條件捨去
區間的範圍 (左閉右開，左閉右閉，左開右開)
紀錄的答案是甚麼意思

\(0, 0, ..., 0, 0, 1, 1, 1, ..., 1\)

這個或這個？

講完了欸

沒有完全聽懂沒關係！

聽懂的話一定要自己實作喔！

二分搜可以很簡單，也可以超難

大家有沒有覺得演算法很有趣呢？

指標與STL

回顧一下之前的內容

C++ 程式結構
輸入輸出
變數，運算子
判斷式，迴圈
陣列
時間複雜度，二分搜尋法

先從變數開始談吧！

之前說過電腦會把變數的值存在記憶體的某個地方

那我們有什麼辦法獲得這個「記憶體位置資訊」呢？

找到一個變數的位置

int main() {
    int a = 3;
    cout << &a << endl;
}

假設我把「變數位置」存在另一個變數的話...

#include <iostream>
using namespace std;
int main() {
    int a = 3;
    int * point = &a;
    cout << point << endl;
}

等等，所以這些符號的意思？

&: 取址符號，將一個變數的位址取出來

*：指標，一個儲存記憶體位置的資料型別

也是 * : 取值符號，將一個指標指向的值取出來

雖然符號一樣，不過位置不同有不同的功能!

(一個用於宣告，一個用於取值)

Example

#include <iostream>
using namespace std;
int main() {
    int a = 3;
    int * point = &a;
    //這是定義用的*
    cout << *point << endl;
    //這是取值用的*
}

會輸出什麼?

參照

可以想像成一個變數的"別稱"

#include <iostream>
using namespace std;
int main() {
    int a = 3;
    int &point = a;
    cout << point << endl;
}

指標/參照的用途

其實真的很少XDD
對記憶體/陣列做事
讓變數在不同函數間作用
建資料結構
...

STL

是啥?

Soul Translator(X

Standard Template Library(O

可以幹嘛?

偷懶(O

容器

一個裝東西的東西(像陣列)

不同的容器會有不同的功能

STL提供了多種不同的容器供選擇

語法通常長這樣:

容器類別<資料型別> 容器名稱;

Iterator

迭代器

每個陣列都有索引值

"容器的索引值"就是迭代器

大致可分為隨機存取的(直接取某項)

與只能往前或往後走一格的

Vector

可變長度的陣列

#include <iostream>
#include <vector>
using namespace std;
vector<int> v;
int main() {
    v.push_back(7122);
    cout<<v[0]<<"\n";
}

遍歷的方式

vector<int> v;
for(int i=0;i<v.size();i++){
    cout<<v[i]<<" ";
}
/*--------------------------*/
for(auto i:v){
    cout<<i<<" ";
}
/*--------------------------*/
for(auto i=v.begin();i!=v.end();i++){
    cout<<*i<<" ";
}

Pair

就兩個東西綁在一起

#include <iostream>
#include <utility>
using namespace std;
int main(){
    pair<int,int> p = {71,22};
    cout<<p.first<<" "<<p.second<<"\n";
}

Code 好長?

簡化一下

#include <iostream>
#include <utility>
using namespace std;
typedef pair<int,int> pii;
#define F first
#define S second
int main(){
    pii p = {71,22};
    cout<<p.F<<" "<<p.S<<"\n";
}

來實作看看吧!

Q1: 一開始有一個空的可變長度陣列，支援兩種操作:

輸入 \(1 \ x\)，將\(x\)加到最後面

輸入 \(2 \ y\)，輸出陣列倒數第\(y\)個東西

#include<algorithm>

實作了各種常見的演算法

舉個最簡單的例子

#include <iostream>
#include <algorithm>
using namespace std;
int main(){
    int a, b;
    cin>>a>>b;
    cout<<max(a,b)<<"\n";
}

Sort

複習一下 Bubble Sort

給定一個長度為\(N\)正整數序列，將其由小到大排序

想法: 從左到右依序考慮每對相鄰的數，

如果左邊比右邊大就交換，

於是最大的一定會到最右邊，

所以重複\(N\)次就做完了。

要跑多久?

STL Sort

#include <iostream>
#include <algorithm>
using namespace std;
int arr[100];
int main(){
    sort(arr,arr+100);
}

複雜度: \(O(NlogN)\)

如果想從大排到小...

#include <iostream>
#include <algorithm>
using namespace std;
int arr[100];
bool cmp(int a, int b){
    return a>b;
}
int main(){
    sort(arr,arr+100,cmp);
}

當然，比較方式也可以全照自己高興

lower_bound

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> v;
int main(){
    cout<<lower_bound(v.begin(),v.end(),7122)-v.begin();
}

回傳一個迭代器，表示陣列中

"第一個 \(\geq x\)" 的位置 (需先排序好)

時間複雜度: 隨機存取迭代器\(O(logN)\)，其他\(O(N)\)

注意事項

STL的每個功能都有需引入的標頭檔

如果懶得記可以寫

#include<bits/stdc++.h>

絕大部分平常用的到的功能都在裡面

再來練習吧

Q2: 輸入\(n\)個數字的陣列，輸出兩行:第一行輸出所有奇數由小排到大，第二行輸出所有偶數由小排到大

再來練習吧

Q3: 第一行輸入兩個數字 \(n, m\)，接下來有\(n \times m\)個數字，請將這些數字重新排列，使得任何一個數字的左邊跟上面都不比他小

我是防雷線

Queue

先進先出

			5	8	7	4

Queue

先進先出

#include <iostream>
#include <queue>
using namespace std;
queue<int> que;
int main(){
    que.push(5);
    que.push(3);
    cout<<que.front(); //5
    que.pop();
    cout<<que.front(); //3
}

Stack

後進先出

			5	8	7	4	10

Stack

後進先出

#include <iostream>
#include <stack>
using namespace std;
stack<int> stk;
int main(){
    stk.push(5);
    stk.push(3);
    cout<<stk.top(); //3
    stk.pop();
    cout<<stk.top(); //5
}

Deque

兩端的先進先出

#include <iostream>
#include <queue>
using namespace std;
deque<int> deq;
int main(){
    deq.push_front(5);
    deq.push_back(3);
    cout<<deq.front(); //5
    cout<<deq.back(); //3
    deq.pop_front();
    deq.pop_back();
}

Linked List

可以支援中間插入、刪除

Linked List

可以支援中間插入、刪除

#include <iostream>
#include <queue>
using namespace std;
deque<int> deq;
int main(){
    deq.push_front(5);
    deq.push_back(3);
    cout<<deq.front(); //5
    cout<<deq.back(); //3
    deq.pop_front();
    deq.pop_back();
}

函數與遞迴

先來談談數學中的函數吧！

一般會用 \(f(x) = y\) 表示

其中 \(f\) 稱為函數

\(x\) 是輸入值

\(y\) 是輸出值

ex. \(f(x) = 71x + 22, f(a, b) = 3a^3 - b^2\)

C++ 裡面的函式

C++的函式需要如此定義：

int func(char input) {
    // do stuff
    return output;
}

函數名稱：func

輸入：input

輸入型別：char

輸出：output

輸出型別：int

函式宣告的位置

#include <iostream>
using namespace std;
int func(char input) {
    // do stuff
    return output;
}
int main() {

}

一般是寫在 #include 之後，main 函式前面

函式的使用

#include <iostream>
using namespace std;
int func(char input) {
    // do stuff
    return output;
}
int main() {
    cout << 2 + func('a') << endl;
}

把他當成是「回傳型別」的那個東西來用

試試看吧

#include <iostream>
using namespace std;
int f(int a) {
    return 2 * a + 1;
}
int main() {
    cout << f(3) << endl;   //7
    cout << f(5) << endl;        //11
    cout << f(f(3) + 3);                 //21
}

以下程式每一行分別會輸出什麼？

試試看吧 Part 2

#include <iostream>
using namespace std;
int f(int a, int b) {
    return (a + 3) * (b + 2);
}
int main() {
    cout << f(3, 4) << endl;          //36
    cout << f(f(1, 2), 3) << endl;            //95
}

以下程式每一行分別會輸出什麼？

試試看吧 Part 3

#include <iostream>
using namespace std;
int f(int a) {
    return a + 2;
}
int g(int a) {
    return a / 2;
}
int main() {
    cout << f(3 + g(5)) << endl;      //7
    cout << f(g(f(10))) << endl;            //8
}

如果有好幾個函式呢？

注意到：當我們有好幾的函式包在一起的時候，計算順序是

由內而外

來練習一個題目吧

實作一個函式，輸入兩個點的座標（四個整數\(x1, y1, x2, y2\)），輸出兩點之間的距離平方

Hint: \((x1 - x2)^2 + (y1 - y2)^2\)

int dist(//four numbers) {
    return .....
}
int main() {
    cout << dist(1, 0, 2, 2) << endl;
    //5
    cout << dist(3, 2, 1, 2) << endl;
    //4
}

void

適用於函數沒有回傳值的時候

void printarr(vector<int> v){
    for(int i=0;i<v.size();i++){
        cout<<v[i]<<" ";
    }
    cout<<"\n";
}

函數套函數套函數

\(f(f(f(......f(x))))\) 不知道有幾個怎麼辦？

在函式裡面呼叫自己？！

int f(int x) {
    return f(x - 1) + 1;
}

遞迴：函數呼叫自己

int f(int x) {
    return f(x - 1) + 1;
}

這樣其實會跑不完www

int f(int x) {
    if (x <= 0) return 0;
    return f(x - 1) + 1;
}

呼叫\(f(5)\)時會輸出什麼呢？

跟著程式的流程看

f(3) = 3

f(2)+1

f(1)+1

f(0) + 1

return 0;

再看一個

費氏數列：

int fib(int x) {
    if (x == 0) return 1;
    if (x == 1) return 1;
    return fib(x - 1) + fib(x - 2);
}

f(3) = 3

f(2)=2

f(1)=1

f(0)=1

遞迴的寫法

邊界條件/初始值
遞迴式

遞迴的想法

把問題拆成大問題跟小問題
每個問題都有固定的做法
終止條件

實作練習 - 最大公因數

大家有聽過輾轉相除法嗎？

\(gcd(0, b) = b\)

\(gcd(a, b) = gcd(b \ mod \ a, a) \)

證明...有時間再說吧XD

實作練習 - TIOJ 1060 函數計算

https://tioj.ck.tp.edu.tw/problems/1060

輸入一個數字 \(x(-300 < x < 300)\) ，請計算 \(f(x)\)。

難題 - 河內塔

把左邊的每個環移到中間，一次只能搬一個環，而且上面的環一定要比下面小。

拆成小問題!

字元、字串、

類別(struct)

回到資料型態吧

int, long long 這些都是整數

還有一個東西叫做char!

char: 就是字元

C++ 的字元表示-ASCII

把常見的字元（英文）

放進一個整數裡面

https://zh.wikipedia.org/wiki/ASCII

常用字元ASCII 碼

'0' -> 48

'A' -> 65

'a' -> 97

相鄰(相近）的字元會在ASCII的相鄰位置！

跳脫字元

像是「換行」這種東西有沒有字元怎麼辦？

其實有欸

'\n' -> 換行

'\t' -> tab

'\\' -> \

那要怎麼從 int 跟字元之間互相轉換？

int main() {
    cout << char(67) << endl;
    cout << int('A') << endl;
    cout << char('A' + 5) << endl;
}

注意，字元之間本來就可以跟整數/其他字元相加！

範例：判斷字元是否在0~9間

int main() {
    char c;
    cin >> c;
    if ('0' <= c && c <= '9') {
        cout << "is digit" << endl;
    } else {
        cout << "not digit" << endl;
    }
}

字串：一堆字元和起來

其實就是字元的陣列www

int main() {
    char str[100];
    cin >> str; //or scanf("%s", str)
    cout << str << endl;
}

注意，超過一百的字元的話會爆掉

遇到空白或換行就會停掉

但是這樣要怎麼知道我輸入了幾個字元呢？

int main() {
    char str[100];
    for (int i = 0;i < 100;i++) str[i] = 0;
    cin >> str; //or scanf("%s", str)
    for (int i = 0;i < 100;i++) {
        if (str[i] == 0) {
           cout << "length " << i << endl;
           break;
        }
    }
}

是不是有點麻煩www

還好，我們學的是C++

string: 幫你寫好很多東西的字元vector

是個可變長度的陣列

int main() {
    string s;
    cin >> s;
    cout << s << endl;
}

String 到底多好用呢？

用法基本上跟vector 一樣，還更多

int main() {
   string s;
   cin >> s;
   cout << s.size() << endl;
   s += "7122";
   for (int i = 0;i < s.size();i++) {
       cout << s[i] << endl;
   }
   sort(s.begin(), s.end());
   reverse(s.begin(), s.end());
   cout << s << endl;
}

取長度： s.size()

後面加東西： +=

排序：sort

倒過來:reverse

輸入一整行的話

使用cin.getline()

int main() {
   string s;
   char arr[100];
   cin.getline(arr); //for 字元陣列
   getline(cin, s);
}

來練習一下吧！

輸入一個可能有 0~9, a~z, A~Z 的字串，請把a~z, A~Z去除，輸出數字的部分

來練習一下吧！Part 2.

輸入一個很大的整數（超過18位），輸出他除以 3 的餘數。

提示：一個數字除以3的餘數是所有位數加起來除3的餘數

換個主題囉

假設你需要一個東西可以放3 個int，2 個bool，5個char的話，然後c++又沒有這種東西怎麼辦？

使用struct!

struct 是自定義類別（結構），簡單來說就是C++ 沒有的東西你可以自己寫！

struct object{
    int a, b;
    char c;
    
};

一個類別需要什麼東西？

裡面放變數或函式！

struct object{
    int a, b;
    char c;
    int sum() {
        return a + b;
    }
};

struct 的宣告方法

struct object{
    int a, b;
    char c;
    object() {
        a = 0, b = 0, c = 'a';
    }
    object(int d) {
        a = d, b = d + 5, c = 'A';
    }
    void QQ() {
        cout << a + b << " QQ~" << endl;
    }
};

int main() {
   obj ob = object(4);
   ob.QQ();
}

struct 的使用方法

struct object{
    int a, b;
    char c;
    object() {
        a = 0, b = 0, c = 'a';
    }
    object(int d) {
        a = d, b = d + 5, c = 'A';
    }
};
int main() {
    object obj = object(3);
    obj.b += 4;
    cout << obj.b << endl;
}

C++ 中的物件導向

很多的功能都是用物件(template, class, struct...)包起來，要用他的東西或函式就是用那個東西加上"."。

貪心法

解題的方式？

程式競賽的題目，常常會要你對原本的資料做一些操作，或是找到一組解，使得這組解最好。

有時候，一直做同一件事/使用一個簡單的判定條件就會是最好的答案了！

來看一個例題吧

2020全國賽pA

有\(n\)種礦物，每個礦物有重量\(w_i\)和每單位重量的價值\(v_i\)。你可以選總重\(C\)的礦物，每次必須選一單位重量。請問最多可以獲得多少價值？

\(n \leq 10^5, w_i, v_i, C \leq 10^9\)

怎麼樣會最好？

啊不就是取價值最高的東西...

但是為什麼？

Greedy 的證明方法

如果我有一組其他的解，那我一定可以改這一組解讓他變得更好。

例如：

1	2	3	3	4	5
1	2	3	4	5	5

再看一題

CF Goodbye 2020 pB

給你一些數字，對於每個數字可以選擇他要\(+1\)還是維持原狀。請問新的序列最多有多少種不同的數字。

\(n \leq 10^5\)

是不是比較難想？

那到底要怎麼做呢？

許多Greedy 的題目都需要考慮數字的大小，因此「排序」會是好的第一步。

假設數字由小到大排好呢？

1	1	3	3	3	4	5	5

把所有的可能列下來

1	1	3	3	3	4	5	5

不加一個東西，不影響答案 -> 沒事
加了一個東西，答案\(+1\) -> 前面有重複，後面沒有東西
加了一個東西，答案\(-1\) -> 前面沒重複，後面有東西
加了一個東西，答案不變 -> 前後都重複

只要「前面有重複」，那麼增加一個東西一定不會把答案變差！

結論

排序好之後，從數字小的做到數字大的。如果目前的數字不比前面的數字大，就可以把那個數字加一。

實作！

//Challenge: Accepted
#include <iostream>
#define maxn 100005
#define Goodbye2020 ios_base::sync_with_stdio(0);cin.tie(0);
using namespace std;
int a[maxn];
int main() {
	Goodbye2020
	int t;
	cin >> t;
	while (t--) {
		int n;
		cin >> n;
		for (int i = 0;i < n;i++) cin >> a[i];
		for (int i = 1;i < n;i++) {
			if (a[i] <= a[i - 1]) a[i]++;
		}
		int ans = 1;
		for (int i = 1;i < n;i++) {
			if (a[i] > a[i - 1]) ans++;
		}
		cout << ans << "\n";
	}
	return 0;
}

Greedy 的題目千變萬化，沒有固定的解法，所以很難><

誰先晚餐

題敘

寫Greedy ：

想到一個做法
驗證那個做法

按照吃東西的時間排序

為什麼？

答案 = \( \max (之前的人煮的時間 + b_i)\)

再看一題

給你\(n\)個線段，每個線段有左界跟右界\([l, r]\)。請問最多可以選幾個線段，使得這些線段兩兩互不相交？

一樣，用「排序」解決問題！

但是一次只能排序一個東西...

從左邊做到右邊...

目前看完了前\(x\)個線段

那我們會希望右界盡量小！

來個難一點的

https://codeforces.com/problemset/problem/1165/F2

題敘略

可能需要前面學過的技巧?

動態規劃

什麼是動態規劃

動態規劃

Dynamic Programming

DP

簡單來說，DP是一個"將原問題拆成許多子問題，並記錄子問題答案"而達成加速運算的方法

一個非常簡單的問題

計算費氏數列第\(N\)項?

\(N\leq 50\)

long long fib(int n){
    if(n==0) return 0;
    if(n==1) return 1;
    return fib(n-1)+fib(n-2);
}

複雜度?

大約是\(O(2^N)\)

My code runs

as slow as a turTLE?

fib(4)

fib(3)

fib(2)

fib(1)

fib(0)

fib(2)

fib(1)

fib(0)

fib(5)

fib(3)

fib(2)

fib(1)

fib(0)

同樣的東西重複算太多次

long long dp[51];
long long fib(int n){
    if(n==0) return 0;
    if(n==1) return 1;
    if(dp[n]]>0) return dp[n];
    return dp[n]=fib(n-1)+fib(n-2);
}

紀錄子問題的答案

將已經算過的值存在dp陣列中

若發現算過了就直接回傳，不用再遞迴下去

long long dp[51];
int main(){
    int n;
    cin>>n;
    dp[0]=0; dp[1]=1;
    for(int i=2;i<=n;i++){
    	dp[i]=dp[i-1]+dp[i-2];
    }
    cout<<dp[n]<<"\n";
    return 0;
}

也可以這樣寫

使用DP的條件

1. 重複子問題

有很多子問題可歸類為同樣的問題

2. 無後效性

子問題的解在確定後就不受其他決策影響

3. 最優子結構

問題的最優解，是由子問題的最優解合併而來

DP三步驟

1. 狀態

如何記錄子問題的答案

2. 轉移

問題的答案如何藉由子問題求得

3. 基底

遞迴終點 (Base case)

回到費氏數列的例子

1. 重複子問題

同樣的fib(x)被算到很多次

2. 無後效性

fib(x)的答案算完後就確定

3. 最優子結構

fib(x)總是等於fib(x-1)+fib(x-2)

回到費氏數列的例子

1. 狀態

dp[i]=費氏數列第 i 項

2. 轉移

dp[i]=dp[i-1]+dp[i-2]

3. 基底

dp[0]=0, dp[1]=1

複雜度?

DP的複雜度通常是"狀態*轉移"

狀態: \(O(N)\)

轉移: \(O(1)\)

總複雜度: \(O(N)\)

題外話: 使用某些技巧可以優化至\(O(logN)\)

再使用某些技巧可以優化至\(O(1)\)~~(存月球)~~

經典問題

最大連續子序列

有一個長度為\(N\)的整數序列，求總和最大的連續子序列(可以為空)的總和

\(N\leq 10^6\)

最大連續子序列

1. 狀態

dp[i]=以第 i 項結尾的最大連續和

答案為 \(\max_{i=0}^{n} dp[i]\)

2. 轉移

dp[i]=max(dp[i-1],0)+arr[i]

3. 基底

dp[0]=0 (1-base)

複雜度: O(N)

最大連續子序列

const int MAXN=1E6+10;
int arr[MAXN];
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>arr[i];
    }
    int sum=0, ans=0;
    for(int i=1;i<=n;i++){
        if(sum<0) sum=0;
        sum+=arr[i];
        ans=max(ans,sum);
    }
    cout<<ans<<"\n";
    return 0;
}

經典問題

湊零錢

有 \(N\) 個硬幣，第 \(i\) 個硬幣面額為 \(w_i\)，求能否湊出 \(K\) 元

\(N,K\leq 5000\)

湊零錢

1. 狀態

dp[i][j] = 使用前 i 種硬幣能否湊出 j 元

答案為 dp[n][k]

2. 轉移

dp[i][j] = dp[i-1][j] | dp[i-1][j-w[i]]

3. 基底

dp[0][0]=1

複雜度: 時間O(NK)、空間O(NK)

滾動DP

剛剛的湊零錢問題，可以發現dp[i]的值只跟dp[i-1]有關

當我們把dp[i]的值都算好，dp[i-1]的值就可以丟掉了

空間複雜度節省至O(K)

此技巧稱為滾動dp

經典問題

湊零錢之二

有 \(N\) 種硬幣，第 \(i\) 種硬幣面額為 \(w_i\)，求湊出 \(K\) 元所需最少硬幣數，若無法達成輸出-1

\(N,K\leq 5000\)

湊零錢之二

1. 狀態

dp[i][j] = 使用前 i 種硬幣湊出 j 元所需最少硬幣數

答案為 dp[n][k]

2. 轉移

dp[i][j] = min(dp[i-1][j], dp[i-1][j-w[i]]+1)

3. 基底

dp[0][0]=1，其他設為無限大

複雜度: 時間O(NK)、空間O(K)(滾動)

經典問題

01背包

有 \(N\) 個物品，第 \(i\) 個物品有重量 \(w_i\) 與價值 \(v_i\) ，你有一個容量為\(M\)的背包，求在物品重量總和不超過\(M\)的前提下，所能得到的最大價值總和

\(N,M\leq 5000\)

01背包

1. 狀態

dp[i][j] = 使用前 i 個物品，在重量不超過 j 的情況下所能得到的最大價值

答案為 dp[n][m]

2. 轉移

dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])

3. 基底

設為全0

複雜度: 時間O(NK)、空間O(K)

實作練習

https://tioj.ck.tp.edu.tw/problems/1354

https://tioj.ck.tp.edu.tw/problems/1097

題敘省略

經典問題第二彈

最長遞增子序列(LIS)

有一個長度為 \(N\) 的序列，第 \(i\) 項為 \(a_i\)，求最長遞增子序列的長度

\(N\leq 5000, a_i\leq 10^9\)

LIS

1. 狀態

dp[i]: 以第 i 項結尾的LIS長度

答案為 \(\max\limits_{1\leq i\leq n} dp[i]\)

2. 轉移

\(dp[i] = \max\limits_{j<i, a_j<a_i} dp[j]+1\)

3. 基底

設為全0

複雜度: 時間\(O(N^2)\)、空間\(O(N)\)

經典問題第二彈

https://tioj.ck.tp.edu.tw/problems/1175

進階版LIS

有一個長度為 \(N\) 的序列，第 \(i\) 項為 \(a_i\)，求最長遞增子序列的長度

\(N\leq 10^5, a_i\leq 10^9\)

進階版LIS

1. 狀態

dp[i][j]: 考慮序列的前 i 項，長度為 j+1 的LIS中，最後一項的最小值。若不存在則設為無限大。

答案為dp[n]答案為無限大的最小 j。

2. 轉移

\(dp[i][j] = a_i\) if \(a_i\geq dp[i-1][j-1]\And a_i<dp[i-1][j]\)

\(dp[i-1][j]\) else

3. 基底

全設為無限大

複雜度: 時間\(O(N^2)\)、空間\(O(N^2)\)(還是過不了?)

觀察一下

dp[i]只跟dp[i-1]有關

將 i 維度滾掉，空間降至O(N)

對於所有 i，dp[i]遞增

比較長的LIS，最後一項一定比較大

從dp[i-1]轉移至dp[i]時，只有一項會改變

dp[i-1]中，第一個大於\(a_i\)的項會改成\(a_i\)

二分搜找到那一項

複雜度: 時間\(O(NlogN)\)、空間\(O(N)\)

經典問題第二彈

最長公共子序列(LCS)

有兩個長度為 \(N\) 的序列，求兩序列的最長公共子序列的長度

\(N\leq 5000\)

LCS

1. 狀態

dp[i][j]: 考慮第一個序列前 i 項與第二個序列前 j 項，他們的LCS長度

2. 轉移

\(dp[i][j] = \max(dp[i-1][j-1]+1\), if \(a_i==b_j\)

\(\max(dp[i-1][j], dp[i][j-1]))\)

3. 基底

設為全0

複雜度: 時間\(O(N^2)\)、空間\(O(N^2)\)

實作練習第二彈

https://tioj.ck.tp.edu.tw/problems/1288

https://tioj.ck.tp.edu.tw/problems/1924

https://tioj.ck.tp.edu.tw/problems/2173

題敘省略

分治法

Divide and Conquer

分治的過程

將大問題切成小問題
「遞迴」解決小問題
「合併」小問題的答案

又或是可以這麼理解

把問題切成很多小的部分
先解決小問題
用小問題的答案處理大問題

什麼時候用？和DP的差別？

1. 重複子問題

~~有很多子問題可歸類為同樣的問題~~

2. 無後效性

子問題的解在確定後就不受其他決策影響

3. 最優子結構

問題的最優解，是由子問題的最優解合併而來

分治切出來的小問題通常不會算到同一個

回到最基本的排序

給你一個整數序列，把他的數字由小到大排序

以下會比較兩種常見的做法:

泡沫排序 (Bubble Sort)

合併排序　(Merge Sort)

泡沫排序

想法：假設前\(i - 1\)項都已經被排序好，要怎麼新增第\(i\)項讓前\(i\)項都被排序?

[2, 3, 7, 14, 49], [24]

Ans: 從右邊做到左邊，如果左邊的數字比右邊大就交換，否則就 break。

複雜度 \(O(n^2)\)

分治的方法

1. 把大小為\(n\)的問題切成大小為\(n - 1\)和\(1\)的問題。

2. 遞迴解決(只剩一個數字時就不用排序了)

3. 合併(交換)

切的方法感覺不太平均?

合併排序

假設有兩個排序好的序列 \(a, b\)，要如何把他們合併成一個排好的序列?

1	3	5	8	9
1	2	2	7

可以在\(O(|a| + |b|) = O(n)\)之內做完!

時間複雜度

每次我在分成小問題時把原本的序列盡量平均的切成兩半

2 1 4 4,7 8 3 6 4,7

1,2 4,4,7 3,8 4,6,7

7 4 4 7

1,2,4,4,7 3,4,6,7,8

1,2,3,4,4,4,6,7,8

有 O(logn)層

每層都是O(n)

共O(nlogn)

分治的時間複雜度分析

aka 主定理 Master's Theorem

(講師也不會的東西）

簡單的例題

APCS 2020 10月第四題: 低地距離

實際的概念就是對於每個數字\(x\)，找到有幾個數字序列位置在他左邊而且比他小。

序列長度 \(\leq 2 \times 10^5\)

提示:利用 merge sort的方法!

利用分治

原問題: 在一個序列中找有

多少組\(i, j\)符合\(i < j, a_i < a_j\)

1. 把序列切成兩半，有三種狀況

都在左邊
都在右邊
跨左右

遞迴解決

合併的時候

[2, 4, 6, 7, 7, 7, 9] [7, 14, 49]

已經保證右邊的序列數字都比左邊序列的數字還右邊了

在放右邊數字的時候，比他小的左邊數字一定被放過，比他大的一定沒有!

只要記錄合併時目前有幾個左邊的東西被放置就好!

Q1. 太陽軍團（從資芽偷起來）

有一個 \(n\)列\(m\)行的正整數矩陣，要問你每ㄧ列的最大值，但你不知道矩陣長什麼樣子，只能詢問某一個位置的數值。保證每一列的最大值位置嚴格遞增。

n \leq m \leq 10^6, Query \leq 10^8

Q2. 資芽

這題好難><

我好像也不太會做

快速冪

問題: 求出\(a^b\) (可能要模\(p\)的餘數)

最簡單的作法: \(O(b)\)次乘法

可不可以更快?

性質

指數律: \(a^{b + c} = a^b \times a^c\)
任意一個正整數都可以用一些二的冪次的和湊出來
\(a^{2b} = a^b \times a^b\)

有想到甚麼嗎?

作法

我能在\(O(\log b)\)找出\(a^1, a^2, a^4, a^8, ..., a^{2^k}\)次方的值，再利用\(b\)的二進位表示法湊出答案!

這也可以用在矩陣上喔

費式數列續

求出費式數列的第\(n\)項模\(10^9 + 7\)，\(n \leq 10^{18}\)

顯然\(O(n)\)太慢了?

矩陣與線性變換?

矩陣乘法?

應用: Karatsuba

大概就是快速的做乘法?

應用: FFT 快速傅立葉變換

大概就是快速的做乘法?

還有很多很多

但是他們都被分類在資料結構，圖論等領域裡了

四校放學社課-C++與演算法 (社團)

By justinlai2003

四校放學社課-C++與演算法 (社團)

2,137

C++與演算法

by 建國中學 賴昭勳 張均豪

C 與 C++ 介紹

程式語言...?

人類和電腦溝通的工具

一個功能多很多的計算機（？

高階 v.s. 低階語言

人工智慧、遊戲製作、網頁處理...

那C跟C++又是什麼？

編譯與執行

編譯：電腦（編譯器）將程式碼自動翻譯變成組合語言（電腦看得懂的指令）。

執行：將編譯後的程式使用。

開發環境介紹

Codeblocks!

Dev C++

之後的活動

APCS

aka 後測大賽&&爛筆試

NPSC

aka 建中被debuff的神奇團體比賽

HP Codewars

aka Cosplay + 吃東西(今年沒有） 歡樂賽

資芽

aka 認識隱藏版電神+國手電神課程

YTP

aka 爽領一萬八的比賽

ISSC

aka 可以出國的神奇比賽

Hello, World!

C++ 程式的組成

1. 標頭檔

2. 命名空間

3. 主函式

\注意/

自己試試看吧！

資料型別與變數

C++ 如何儲存資料

變數

儲存資料的地方

可以想成「記憶體中的某個放東西的位置」

有了變數可以做什麼？

運算子(operator)

int 的運算子

實作練習：

每次進去程式改太麻煩了！

用輸入函式跟終端機互動！

實作time

把剛剛的程式修改成可以輸入的

條件判斷

如果...那麼...

布林值是啥？

一個可以存取「是」或「否」的型別

是：正確的，否：錯誤的

如果...那麼...

控制哪一些程式被執行！

關係運算子

== (不是表情符號）

其他關係運算子

回到剛剛的程式

不覺得有點冗嗎

如果...否則

現在，來點更複雜的

布林值之間的運算子

把兩個條件看成布林值來做運算

布林值之間的運算子

如果...否則如果...否則

練習時間！

奇偶性判斷

Hint: 還記得剛剛講運算子的時候有一個東西叫做取模 (%) 嗎？

閏年判斷

仔細看條件吧！

最後一題！

輸入兩個數字\(a, b\)

邏輯大挑戰？！

迴圈

有一些東西要重複很多次，甚至不知道要做幾次，怎麼辦？

用迴圈!!!

while 迴圈

飯粒

while 的使用時機

by 建國中學賴昭勳張均豪

aka Cosplay + 吃東西(今年沒有）歡樂賽