Binary Search
Motivation
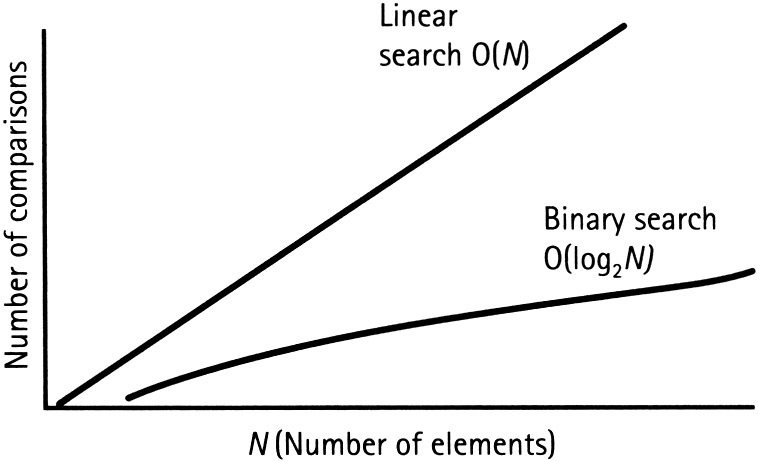
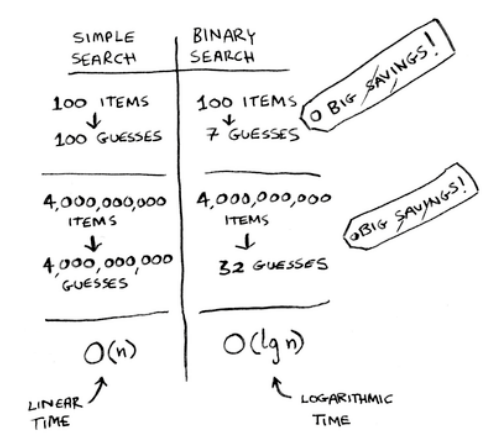
Linear search
Binary search
VS
O( n )
O( log n )
Features
Linear search
- Linear search can be super expensive!
- Need to be allow to random data structure access (e.g. array)


- Data needs to be sorted
- Linear and not linear data structure access allowed (e.g. linked lists)
- Data doesn't need to be sorted
Binary search
- As fast as the wind!
O( n )
O( log n )
Guess my number
Binary Search
Divide and conquer algorithm
Data needs to be sorted
| 1 | 2 | 3 | 4 | 6 | 7 | 9 |
|---|
| 1 | 2 | 3 | 4 | 6 | 7 | 9 |
|---|
| 1 | 2 | 3 | 4 | 6 | 7 | 9 |
|---|
| 1 | 2 | 3 | 4 | 6 | 7 | 9 |
|---|
MID
MID
Find: 6
Implementation
Iterative
function binarySearch(data, target) {
var low = 0,
high = data.length - 1,
mid;
while (low <= high) {
mid = Math.floor((low + high) / 2);
if (data[mid] < target) {
low = mid + 1;
} else if (data[mid] > target) {
high = mid - 1;
} else {
return mid;
}
}
return -1;
}(JavaScript)
Implementation
Recursive
function binarySearchRecursive(data, target, low, high) {
if (low > high) return -1;
var mid = Math.floor((low + high) / 2);
if (data[mid] < target) {
return binarySearchRecursive(data, target, mid + 1, high);
} else if (data[mid] > target) {
return binarySearchRecursive(data, target, low, mid - 1);
} else {
return mid;
}
}(JavaScript)
Options that we have
-
Sort the collection if it is not
-
Make sure that the collection is sorted as we add elements to it
Binary Search Tree
The collection of items is always sorted
Instead the need of sorting every time we add an element to the collection

Binary Search Tree
Properties
- The left subtree of a node only contains values that are less than or equal to the node's value
- The right subtree of a node only contains values that are greater than or equal to the node's value
- Both subtrees are binary trees
Warning: Don't assume that a binary tree is a Binary Search Tree
Binary Search Tree
| 4 |
|---|
| 3 |
|---|
| 2 |
|---|
| 1 |
|---|
| 6 |
|---|
| 7 |
|---|
| 9 |
|---|
Binary Search Tree
Operations Complexity
| Access | Search | Insertion | Deletion | Access | Search | Insertion | Deletion |
|---|---|---|---|---|---|---|---|
| O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) | O(n) | O(n) | O(n) |
| 4 |
|---|
| 3 |
|---|
| 2 |
|---|
| 1 |
|---|
| 6 |
|---|
| 7 |
|---|
| 9 |
|---|
Worst case
Binary tree from a sorted collection
Average
Exercises
Given a sorted array of n integers that has been rotated an unknown number of times, give an O(log n) algorithm that finds an element in the array. You may assume that the array was originally sorted in increasing order.
EXAMPLE:
**Input**: find 5 in array (15 16 19 20 25 1 3 4 5 7 10 14)
**Output**: 8 (the index of 5 in the array)Exercises
Given a sorted array of strings which is interspersed with empty strings, write a method to find the location of a given string.
find “ball” in [“at”, “”, “”, “”, “ball”, “”, “”, “car”, “”, “”, “dad”, “”, “”] will return 4
find “ballcar” in [“at”, “”, “”, “”, “”, “ball”, “car”, “”, “”, “dad”, “”, “”] will return -1Exercises
Given a sorted (increasing order) array, write an algorithm to create a binary tree with minimal height.
THANKS
References
-
Grokking algorithms
-
Algorithms-in-a-nutshell-in-a-nutshell
-
Cracking the coding interview
-
http://bigocheatsheet.com/
-
CS50 youtube channel
Binary search
By jvalen
Binary search
Binary search features, differences with other mechanisms and exercises related.
- 1,041



