A Compressive Light Field Projection System

Matthew Hirsch & Gordon Wetzstein

Ramesh Raskar

MIT Media Lab - Camera Culture Group

SIGGRAPH 2014

CIS 660 Presentation by Kai Ninomiya
University of Pennsylvania

Overview

  • A glasses-free 3D projector
  • Prior work
    • 3D glasses, Nintendo 3DS, light field projection
  • Topics & Algorithms
    • Light field projection
    • Compression
    • 2D: Superresolution & HDR Projection
  • Evaluation & Summary

Prior technologies

What would this replace?

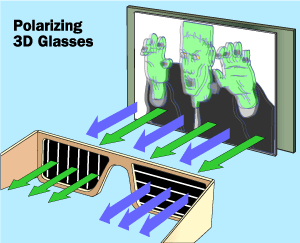
1889: Anaglyphic & 1936: Polarized 3D Glasses

✔ Inexpensive
✔ High resolution
✗ Limited color reproduction
✗ Cumbersome
✗ 2 fixed viewpoints - no parallax

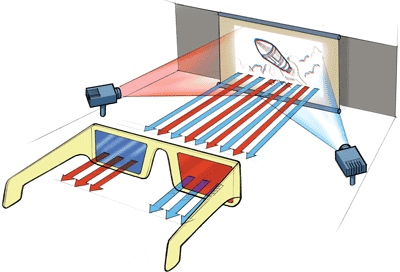
image credit: (a) nerdreactor.com; (b) (c) science.howstuffworks.com

1922: Active Shutter Glasses

✗ Relatively expensive
✔ High resolution
✔ Good color reproduction
✗ Very cumbersome
✗ 2 fixed viewpoints - no parallax

image credit: (a) rtings.com; (b) commons.wikimedia.org

1901: Parallax Barriers & Lenticular Lenses

✗ Relatively expensive
✔ Fairly high resolution
✔ Good color reproduction
✔ Autostereoscopic (no glasses)
✗ Few fixed viewpoints - no parallax

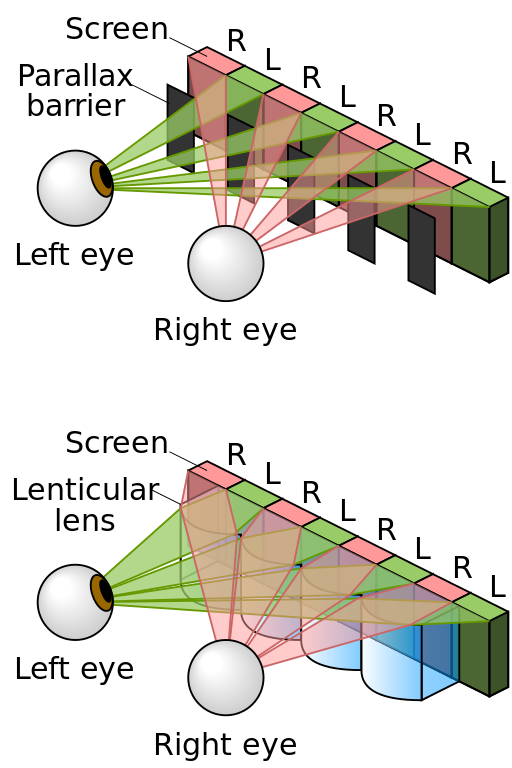
image credit: (a) (b) commons.wikimedia.org

1940: Light Field Projection (Prior Systems)

✗ Very expensive & complex
✗ Reduced resolution
✔ (Sometimes) good color reproduction
✔ Autostereoscopic (no glasses)
✔ Many viewpoints - allows parallax

image credit: (a) National Archives of the Netherlands via Walter Funk, "History of autostereoscopic cinema"; (b) Holografika

Now: Compressive Light Field Projection

✔ Less complex - passive screen
✔ Better resolution
✗ (Currently) no color reproduction
✔ Autostereoscopic (no glasses)
✔ Many viewpoints - allows parallax

Results

What it does and why it's cool

Demos

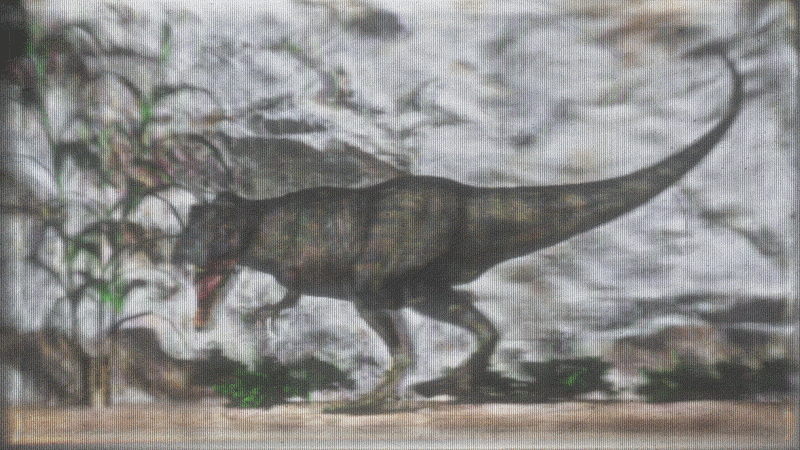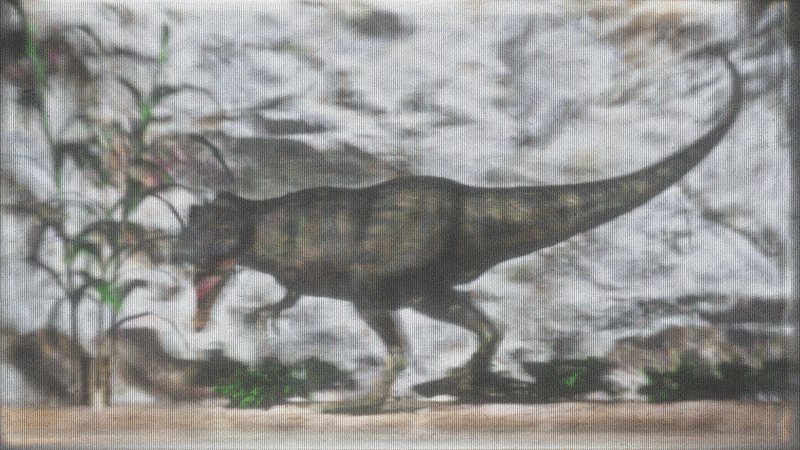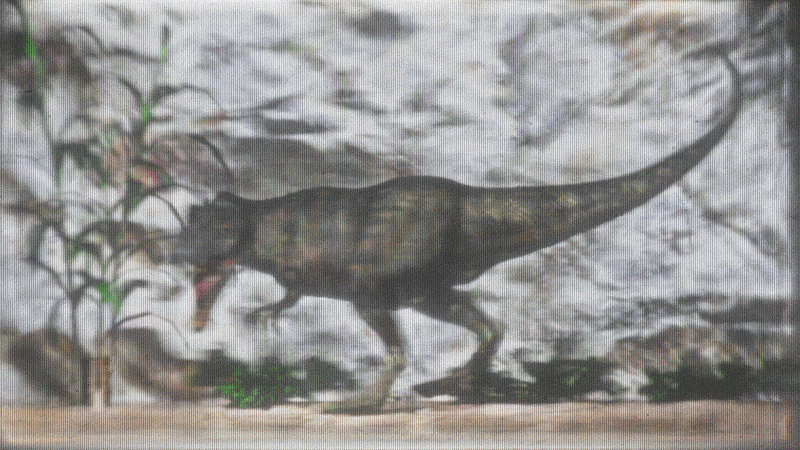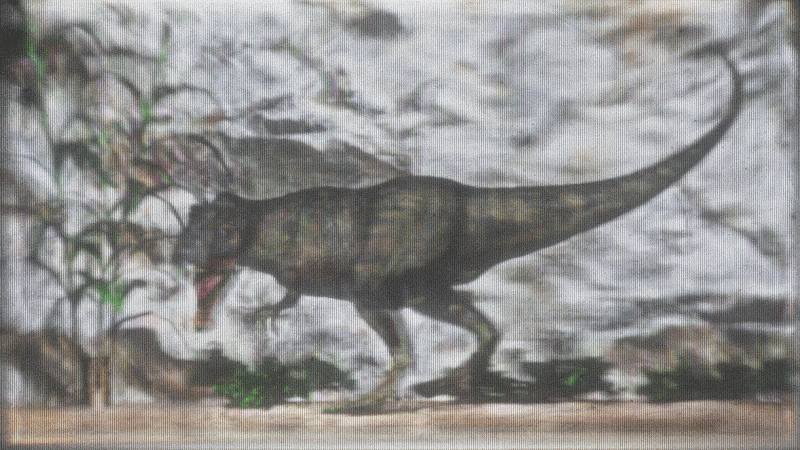
Demos

Demos

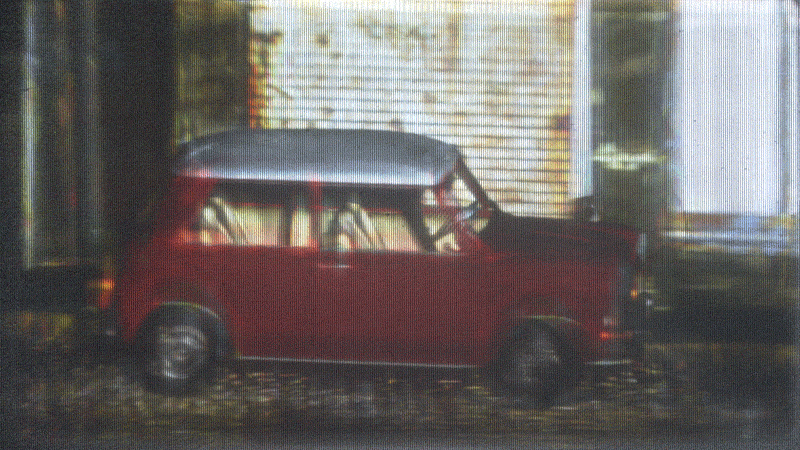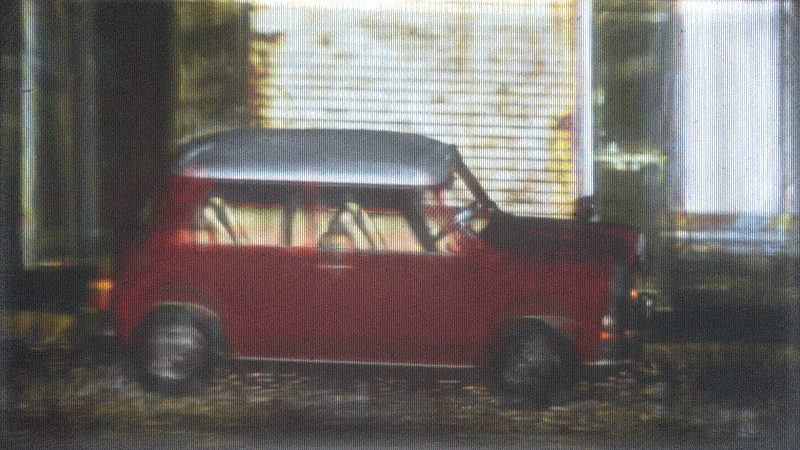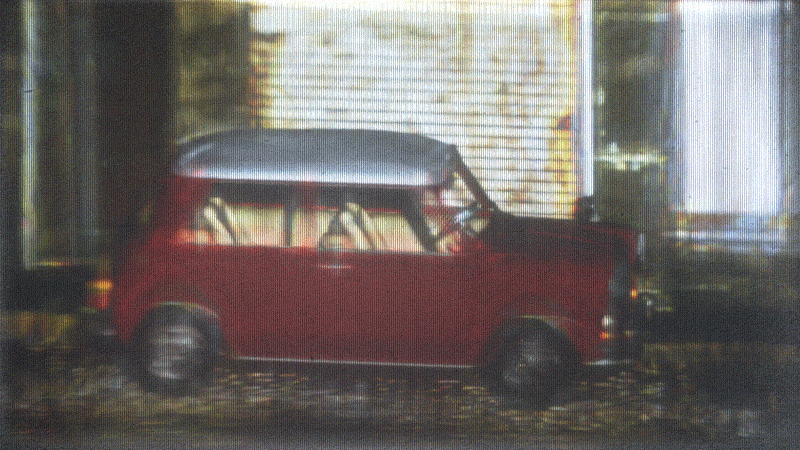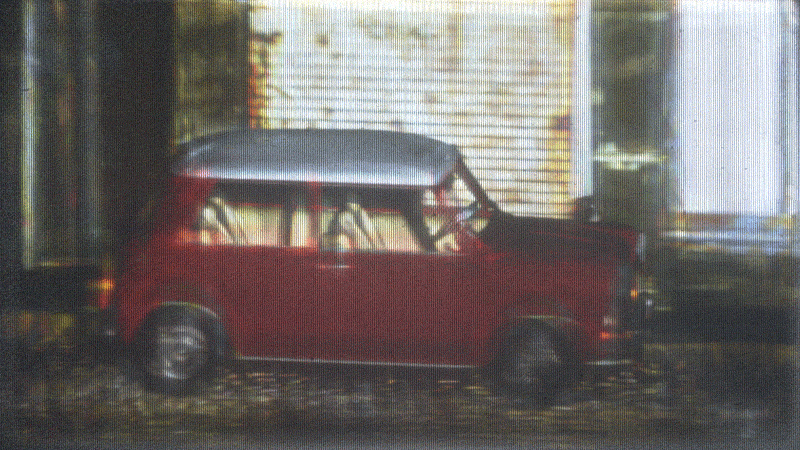
Stats

  • 5° horizontal field of view
  • No color (currently)
    • Demos are 3 grayscale images composited
  • 8 input scene views
    • Compressed

Light Fields

& How can we make them?

Standard Projector

  • Produces a uniform 2D light field
  • Projected onto a diffuse screen
    • View independent: discard angles
\tilde{l}(x,\nu) = g(x)
​l​~​​(x,ν)=g(x)
\nu = \tan\theta
ν=tanθ

Naive Light Field Synthesis

  • Start with standard projector
  • Change screen to prevent diffusion
    • View-dependent: maintain angle
\tilde{l}(x,\nu) = g(\phi(x,\nu))
​l​~​​(x,ν)=g(ϕ(x,ν))
\nu = \tan\theta
ν=tanθ

Naive Light Field Synthesis

  • At each sub-frame, project few rays per pixel
  • Emit pixels onto spatial light modulator (SLM)

 

  • Severe resolution/brightness reduction
    unless using many projectors
\tilde{l}(x,\nu) = g(\phi(x,\nu)) h(\psi(x,\nu))
​l​~​​(x,ν)=g(ϕ(x,ν))h(ψ(x,ν))
\nu = \tan\theta
ν=tanθ

t=1   t=2   t=3

Naive Light Field Synthesis

Getting Better Results

With less hardware

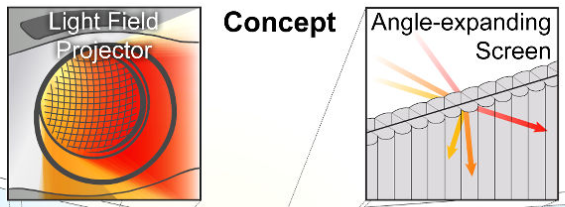
Angle Expansion

  • Want to use one projector
  • Projector output angle is small
    • Won't cover area of audience
  • Expand the angle!
    • Keplerian telescope lensing

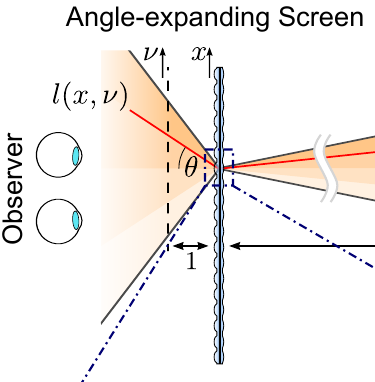
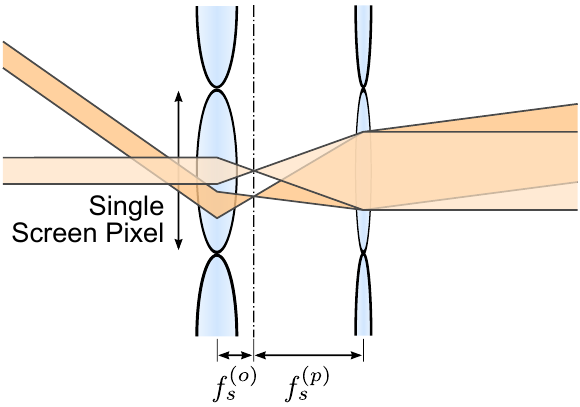
* Ignoring the math here because it isn't very interesting

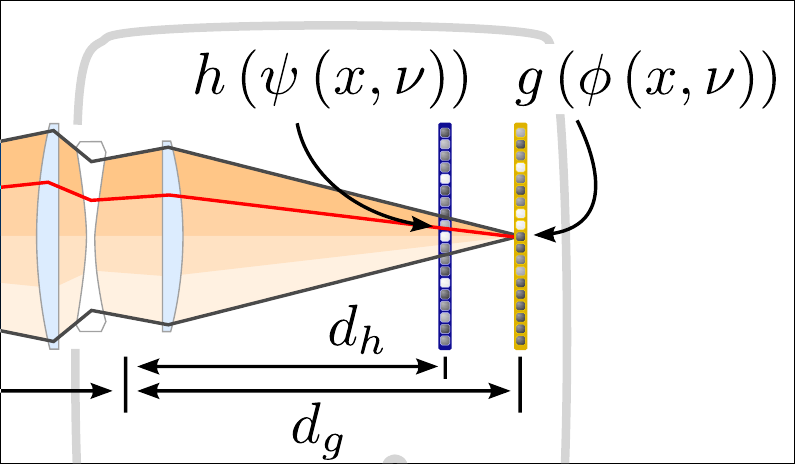
Light Field Compression

  • Finally, the "compressive" part of the title
  • Reduce projected light loss: optical "compression"
  • Reduce data bandwidth: data "compression"

 

  • Basic idea: reuse light for multiple angles

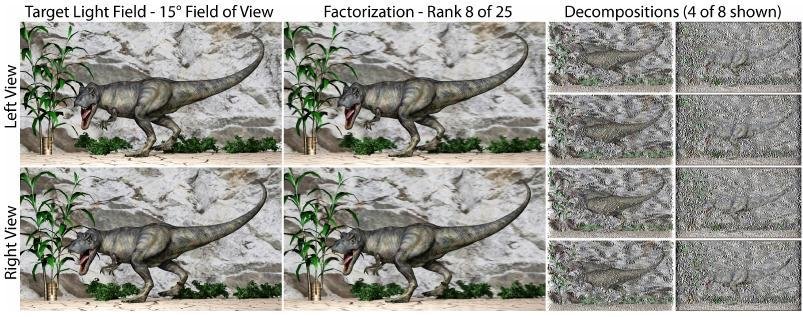
Light Field Compression

  • Optimization solving
    • Find the best sub-frame set of light fields to project
  • Final sub-frame light field is a convolution of SLMs

     
  • Averaged over a frame (due to persistence of vision)

     
  • And minimize against the desired light field
\tilde{l} = (\Phi g) \circ (\Psi h)
​l​~​​=(Φg)∘(Ψh)
\tilde{l} = \frac{1}{T} \sum_{t=1}^{T} (\Phi g_t) \circ (\Psi h_t)
​l​~​​=​T​​1​​∑​t=1​T​​(Φg​t​​)∘(Ψh​t​​)

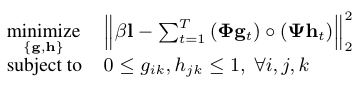
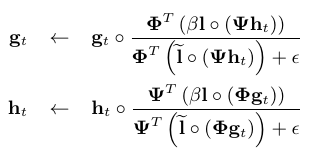
* Capital Greek letters are matrix forms of the functions from before

On Conventional Screens:
2D Superresolution

  • Optimize a convolution again

     
  • Result: Higher effective resolution
    than either individual SLM
\tilde{i} = \frac{1}{T} \sum_{t=1}^{T} (\Phi_{2D} g_t) \circ (\Psi_{2D} h_t)
​i​~​​=​T​​1​​∑​t=1​T​​(Φ​2D​​g​t​​)∘(Ψ​2D​​h​t​​)

On Conventional Screens:
2D High Dynamic Range

  • Use both SLMs to control contrast
    • Gives greater contrast range
  • That's about it

Evaluation & Summary

TL;DR: I thought it was pretty cool.

The Paper Itself

  • Generally well-written
  • A lot of great background information in Related Work
    • Not much background needed to understand
  • Very little (but probably enough) math
    • Makes it easier to work through the paper
    • Excluded: pretty much just optimization algorithms
    • Some details in the paper supplement

The method/results

  • Really cool!
  • The actual contributions:
    • Passive screen
    • Application of compression to that system
    • Demonstration of superresolution

Questions for the Authors

  • The biggest question
    • Why is it monochromatic?
      • Not explained well
    • How constraining is this really?
    • This can be solved with 3 projectors...
      but is there a better way?
  • What is the computation time for the compression solve?
  • Seems good for theaters, but the shape is inconvenient
    • Requires rear projection
    • Any way around this?

Siggraph = very yes

  • Advances the state of the art
    • Higher quality
    • More practical
  • Further refinements needed, obviously
    • But could be very marketable!

A Compressive Light Field Projection System

By Kai Ninomiya

Made with Slides.com

A Compressive Light Field Projection System

  • 433

More from Kai Ninomiya