R
E
A
C
T
O

xamples
epeat
ode
pproach
ptimize
est
{Lattice Paths}

The Question
Given a square grid, how could you determine the number of possible paths from the top left of the grid to the bottom right, assuming you can only move to the right and down?
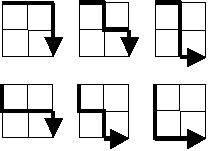
Example: a 2 by 2 grid has 6 possible paths

Same Approach, Different View
(0,0)
(1,0)
(0,1)
(2,0)
(1,1)
(0,2)
(2,1)
(2,2)
(1,1)

(1,2)
(2,2)
(2,1)
(2,1)
(1,2)
(2,2)
(2,2)
(2,2)
(2,2)
(1,2)

Possible Solution
function paths2Bottom(x, y, max){
if (x == max || y == max){
return 1;
}
return paths2Bottom(x+1, y, max) + paths2Bottom(x, y+1, max);
}- Recursive
- Only works for small grids
- Demo of it failing on big grids

Memoized Solution
var paths = {};
function memoizer(x, y, max){
if(paths[[x,y,max]]){
return paths[[x,y,max]];
}
else{
return paths[[x,y,max]] = paths2Bottom(x, y, max);
}
}
function paths2Bottom(x, y, max){
if (x == max || y == max){
return 1;
}
return memoizer(x+1, y, max) + memoizer(x, y+1, max);
}- Still Recursive
- Works on bigger grids

Alternate Approach

When mapping the possible paths, you might see a pattern -- Pascal's Triangle!
We also know that when you hit the right or bottom edge of a grid, there is only one possible path.

Memoized Solution
var paths = {};
function memoizer(x, y, max){
if(paths[[x,y,max]]){
return paths[[x,y,max]];
}
else{
return paths[[x,y,max]] = paths2Bottom(x, y, max);
}
}
function paths2Bottom(x, y, max){
if (x == max || y == max){
return 1;
}
return memoizer(x+1, y, max) + memoizer(x, y+1, max);
}- Still Recursive
- Works on bigger grids

Conclusion
Solution on Repl.it
Source from Project Euler

Copy of Lattice Paths
By Kate Humphrey
Copy of Lattice Paths
Technical interview problem on lattice paths
- 792



