Self-Assembly of DNA Graphs 

Katie Bakewell and Sudam Surasinghe

Presentations and the Like

On Self-Assembly and DNA Graphs

• 2015 International Conference on DNA Computing and Molecular Programming (Harvard University, Boston, Ma)
  • DNA21
• 2015 Southeastern Conference on Combinatorics, Graph Theory, and Computing (FAU, Boca Raton, Fl)
  • World's largest conference on combinatorics
• 2015 Florida AMATYC/MAA joint meeting (Eckerd College, Tampa, Fl)

On Hamiltonian Paths

• 2012 Florida AAMTYC/MAA joint meeting (UNF! Jacksonville, Fl)

Hard Work Pays Off

Details on Self-Assembly

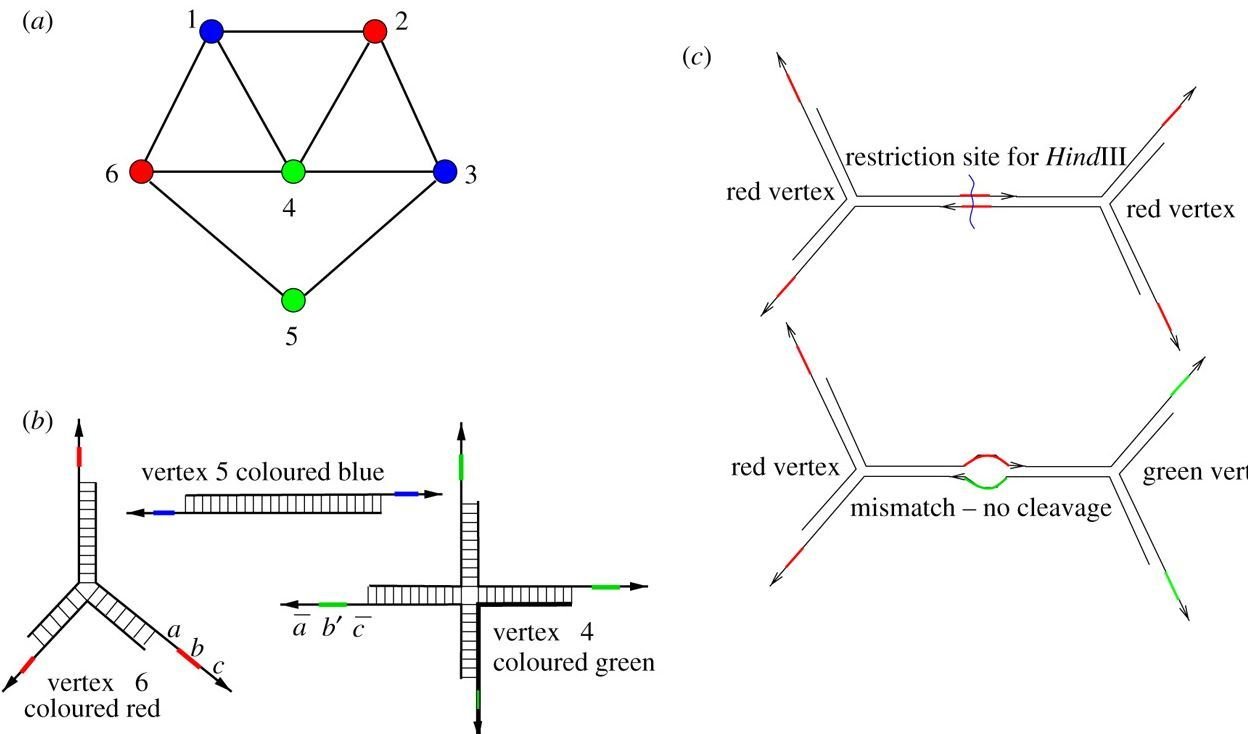
• DNA is made up of two carbohydrate backbones with neucleotide pairs attatching the strands
• Neucleotides A/T or G/C create pairs 
  • Watson Crick Complimentarity
  • Naturally want to bond with each other
• Junction and edge molecules have sticky ends
• When put into ligase, these molecules with sticky ends "assemble" into DNA structures. 

DNA & Graph Coloring 

Graph Theory and Applications

• Another class in the discrete analysis degree track!          
• The study of graph structures (Vertices and Edges)
• HUGELY applicable! 
  • Networking/Network Security 
  • Route optimization 
  • Scheduling
  • Map Coloring

Applying All This

We are working on a problem that uses DNA computing methods (and topology and graph theory too!) to find solutions to postman problems. 

Postman Problems

• A postman has to deliver mail along every street. What is his quickest route? 
  • Sometimes this is an easy problem 

Postman Problems

• A postman has to deliver mail along every street. What is his quickest route? 
  • Sometimes this is an easy problem 
  • Sometimes its a little tricky

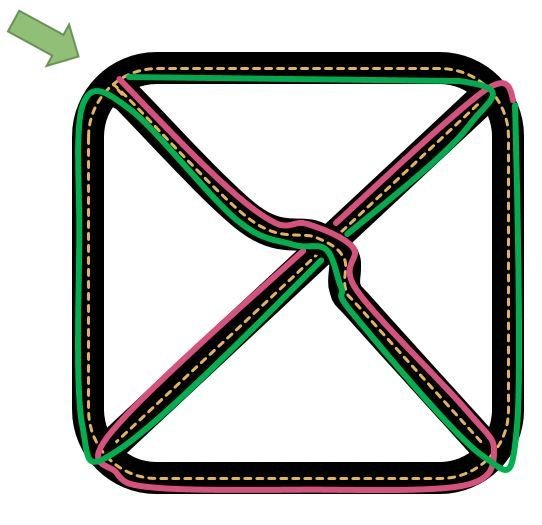
Postman Problems

• A postman has to deliver mail along every street. What is his quickest route? 
  • Sometimes this is an easy problem 
  • Sometimes its a little tricky

Postman Problems

• A postman has to deliver mail along every street. What is his quickest route? 
  • Sometimes this is an easy problem 
  • Sometimes its a little tricky
  • Is this still the quickest solution if it is windy? 

Postman Problems

• A postman has to deliver mail along every street. What is his quickest route? 
  • Sometimes this is an easy problem 
  • Sometimes its a little tricky
  • Is this still the quickest solution if it is windy? 
  • Is it still the quickest solution if one street doesn't have any houses?

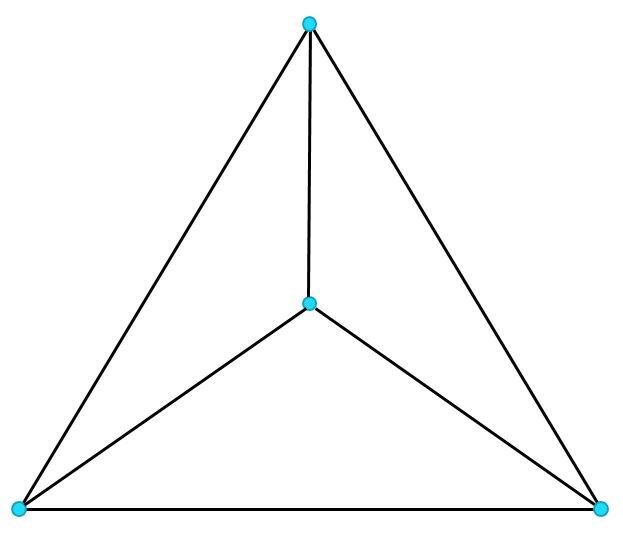
Thickened Graphs

Replacing the edges in a graph with "edge ribbons" gives us a locally two dimensional structure. 

This strucutre allows us to study graphs through their topological structure. 

Our focus is on studying the structure of the boundary components (differently colored segments on the graph).

Boundary Operations

• We can change the number of boundary components by "permuting" the way the edges interact at the vertex. 
• If we do this to multiple vertices, we can get at least one boundary component that traverses every edge at least once. 
  • Called a reporter strand 

Wait...what about DNA?

• In a theoretical world, this is great...we can study graphs through their topology but how do we create all the possible graphs? 
• Enter DNA 
  • Orientable (Watson Crick Complimentarity)
  • Naturally form a 2-d ribbon structure 
  • We can "read" solutions using gel electrophoresis

Searching for Postman Solutions

A reporter strand obviously represents a postman tour...but does the converse hold? Is every postman tour represented by a reporter strand? 

Searching for Postman Solutions

A reporter strand obviously represents a postman tour...but does the converse hold? Is every postman tour represented by a reporter strand? 

Sadly, No. but...

Searching for Postman Solutions

A reporter strand obviously represents a postman tour...but does the converse hold? Is every postman tour represented by a reporter strand? 

Sadly, No. but...

Every postman tour is contained in a reporter strand.

What Are We Doing Now?

Our goal is to remove the extraneous loops that can be created when making a reporter strand that contains a postman tour. 

• Topology of the vertex
• Formal Language Theory
  • Combinatorics of the "word" that is created

Why Study Biomathematics?

• Interesting and Diverse Subject 
  • All kinds of mathematics
  • Interdisciplinary Research
• Unbounded Research Opportunities
• Awesome People
  • 16 Tulip Award Winners 
    • Accessible! 
    • Friendly!
• You get to say DNA Computing!