圖論(一)
建國中學 陳仲肯
目錄
- 圖
- 樹
- 圖的儲存
- 圖的遍歷
- 最短路徑
- 有向無環圖、拓樸排序
- 並查集
- 最小生成樹
我寫過的題目的解可以在這裡找到,這份簡報中的題目都有
抄學長的講義(X
圖
圖(X
圖(O

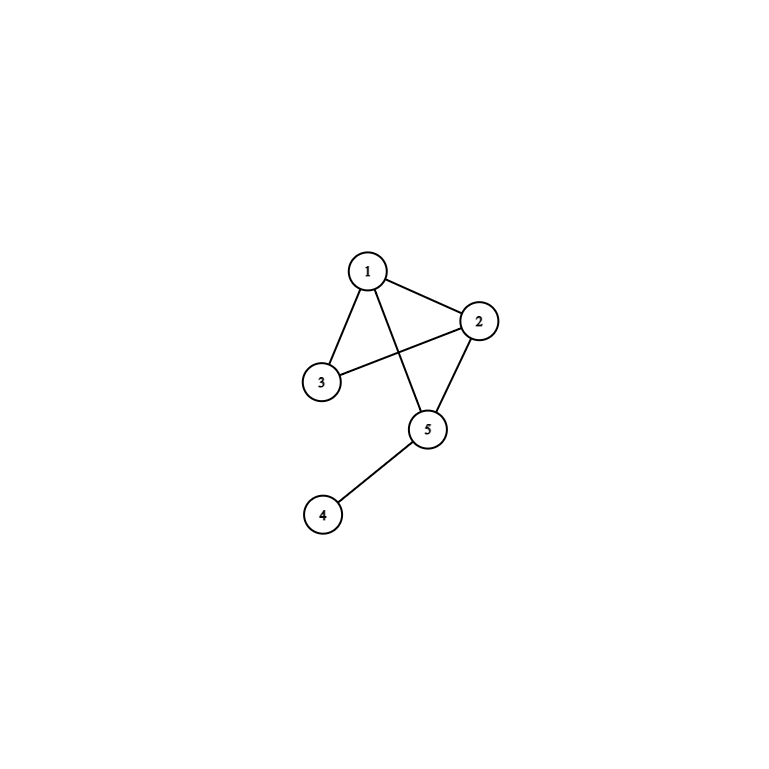

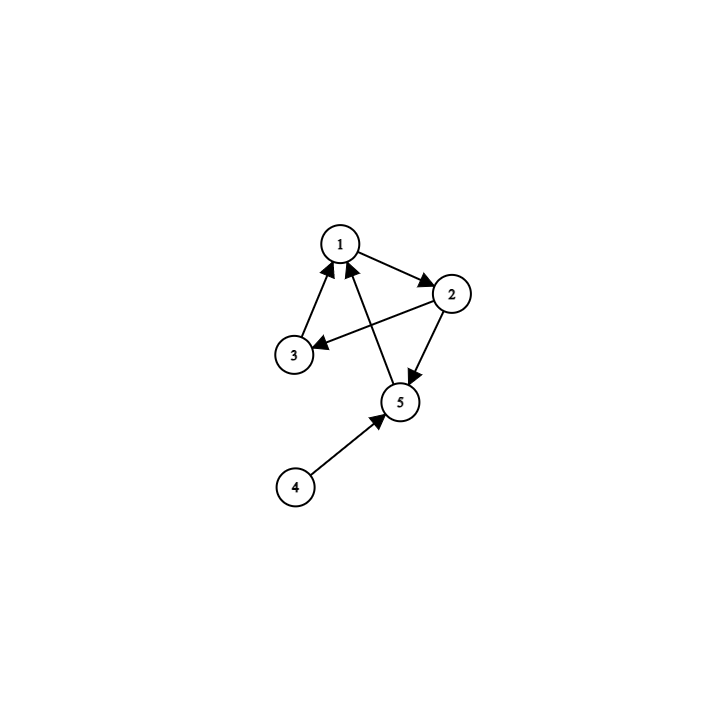
無向圖
有向圖
點
邊
圖=點+邊
有一些點,點和點之間可能會有邊連接
一條邊只能連接兩個點,但一個點可能連出很多條邊
表示一堆東西的關係,比如親戚關係、車站路線
邊可能有「權重」,簡稱邊權,常代表邊的長度
點也可能有點權,例如走到那個點會得到多少錢
1
2
5
3
3
4
6
5
1
奇怪的邊
2
1
重邊
自環
沒有重邊或自環的圖稱為簡單圖
度數
一個點連接的邊數
有向圖的話:
連出去的叫出度
連進來的叫入度
1
2
3
4
5
3
1
1
1
0
相鄰
兩個點藉由一條邊連在一起稱這兩個點相鄰
子圖
從圖中隨便選一些點和邊
1
2
3
4
5
1
2
3
4
路徑
1
2
3
4
5
從一個點開始走,經由一些邊走到一個點
走過的邊就是一條路徑
簡單路徑:沒有重複經過一個點的路徑
環
起點=終點的路徑
1
2
3
4
5
連通、連通分量
連通:圖中任兩點都存在路徑
連通分量:點數盡量多的連通子圖
(可以連的都連起來)
1
2
3
4
5
6
8
7
9
樹
沒有環的簡單連通圖
樹
沒有環的圖,通常會畫成這樣,像是掛在天花板上
1
3
2
4
6
5
根節點
隨便指定的點,通常畫圖時會畫在樹的最上面
1
3
2
4
6
5
- 有根樹:有根的樹
- 無根樹:沒有根的樹,所以可以自己隨便亂設
子節點/兒子:下面(遠離根節點方向)的點
父節點/爸爸:上面(往根節點方向)的點
有根樹中:
子節點/兒子:下面(遠離根節點方向)的點
父節點/爸爸:上面(往根節點方向)的點
有根樹中:
葉節點
沒有子節點的點
1
3
2
4
6
5
7
祖先:
有根樹中:
子孫:
子樹
以X為根的子樹:以X為根,包含X以及X的子孫的樹
1
3
2
4
6
5
以3為根的子樹
深度
到根節點的邊數
1
3
2
4
6
5
1
2
2
3
3
3
高度
最深的點的深度
3
圖的儲存
兩種常用的方法
鄰接矩陣
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 1 | 1 | 0 |
| 2 | 0 | 0 | 1 | 1 |
| 3 | 0 | 0 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 |
1
2
3
4
j
i
若有重邊可以把1改成邊的數量
bool G[N][N];
int n,m;
cin>>n>>m;
int u,v;
for(int i=0;i<m;++i){
cin>>u>>v;
G[u][v]=G[v][u]=1;
}無向圖
兩向的邊都加入
有向圖
實作:輸入圖
bool G[N][N];
int n,m;
cin>>n>>m;
int u,v;
for(int i=0;i<m;++i){
cin>>u>>v;
G[u][v]=1;
}通常會先給你點數、邊數
再給每條邊的起點、終點
有邊權的話
#include <cstring>
bool G[N][N];
int n,m;
memset(G,-1,sizeof(G));
cin>>n>>m;
int u,v,w;//weight
for(int i=0;i<m;++i){
cin>>u>>v>>w;
G[u][v]=w;
}-1代表不可能出現的值,如果有負邊權就改成不可能出現的數
memset(a,b,c):把a開始c個位元都改成b,可以把陣列通通改成一個值,b可以是0,-1,但不能是1,因為位元的特性,-1=滿滿的1
空間複雜度不管多少邊,都是\(O(點數^2)\)
特色
枚舉一個點連出的邊:\(O(點數)\)
枚舉每一條邊:\(O(點數^2)\)
找u到v的邊:\(O(1)\)
鄰接串列
1
2
3
4
1:2,3
2:3,4
3:
4:
實作:輸入圖
用vector
#include <vector>
vector<int> G[N];
int n,m;
cin>>n>>m;
int u,v;
for(int i=0;i<m;++i){
cin>>u>>v;
G[u].push_back(v);
}無向圖就加上
G[v].push_back(u);如果有邊權
#include <vector>
#include <utility>
#define pii pair<int,int>
vector<pii> G[N];
int n,m;
cin>>n>>m;
int u,v,w;
for(int i=0;i<m;++i){
cin>>u>>v>>w;
G[u].push_back({v,w});
G[v].push_back({u,w});
}pair<int,int> 存{點,邊權}
如果覺得pair還要記哪個是哪個很麻煩...
struct E{
int v,w;
};
vector<E> G[N];
//input
G[u].push_back({v,w});
//枚舉一個點連出去的邊
for(auto [v,w]:G[u])這個寫法pair也可用
特色
空間複雜度是\(O(邊數)\)
枚舉一個點連出的邊:\(O(他的度數)\)
枚舉每一條邊:\(O(點數+邊數)\)
找u到v的邊:\(O(u的度數)\)
還有很多存圖方式
比如存邊
-
稠密圖:邊很多的圖,邊數大概是\(點數^2\)
-
稀疏圖:邊很少的圖,邊數大概是\(點數\)
把圖簡單粗暴的分類一下
因為 \(點數-1\le 邊數\le \frac{點數*(點數-1)}{2} \in O(點數^2)\)
空間複雜度是\(O(邊數)\)
枚舉一個點連出的邊:\(O(他的度數)\)
枚舉每一條邊:\(O(點數+邊數)\)
找u到v的邊:\(O(u的度數)\)
空間複雜度:\(O(點數^2)\)
枚舉一個點連出的邊:\(O(點數)\)
枚舉每一條邊:\(O(點數^2)\)
找u到v的邊:\(O(1)\)
鄰接串列
鄰接矩陣
矩陣適用於稠密圖,串列適用於稀疏圖
題目通常是稀疏圖,結論是用串列就好
兩種存圖方法比較
圖的遍歷
DFS、BFS
滿滿題目
遍歷是啥?
目的:把每個點看過一遍
方法:DFS、BFS
DFS(Depth First Search)
深度優先搜尋
- 走到一個點,標示為已經走過
- 拜訪與他相鄰但沒走過的點
- 結束
過程(從1開始DFS)
1
2
3
4
5
1
2
3
4
5
DFS的路徑一定是一棵樹,之後會用到
實作
vector<int> G[N];
bool vis[N];
void dfs(int cur){//current
vis[cur]=1;
for(int nxt:G[cur]){//next
if(vis[nxt])continue;
dfs(nxt);
}
}
int main(){
for(int i=0;i<n;++i){
if(!vis[i])dfs(i);
}
}樹的實作可以省掉vis
vector<int> G[N];
bool vis[N];
void dfs(int cur,int fa){//current, father
for(int nxt:G[cur]){//nxt
if(nxt==fa)continue;
dfs(nxt,cur);
}
}
int main(){
//根是1的連通樹
dfs(1,1);
}特色
超好寫
所以很常用
BFS(Breadth-First Search)
廣度優先搜尋
- 開一個queue存要拜訪的點
- 選擇queue第一個點當作下一個點,並把他劃掉
- 把與他相鄰但沒走過的點加到queue
- 結束
1
2
3
4
5
過程(從1開始BFS)
1
2
3
4
5
實作
#include <vector>
#include <queue>
queue<int> Q;
vector<int> G[N];
for(int i=0;i<n;++i){
//i作為起點
if(vis[i])continue;
Q.push(i);
while(!Q.empty()){
int cur=Q.front();Q.pop();
for(int nxt:G[cur]){
if(vis[nxt])continue;
Q.push(nxt);
}
}
//Q必是空的
}特色
拜訪的節點到起點的最短距離非嚴格遞增
也就是說越先拜訪的點離起點越近
(不管邊權的話)
例題
n=m=0時結束,但n!=0,m=0要做
最短路徑
單點源最短路徑
給你一張帶權圖,求一個點到所有點的最短距離
前提:不能有負環
不然可以一直繞
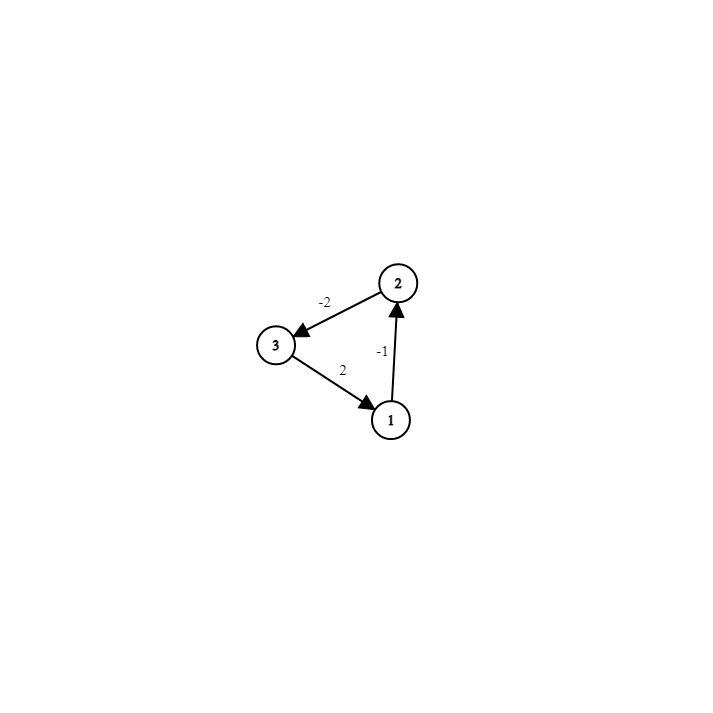
名詞:鬆弛(Relaxation)
繞其他邊可能會更好
起點到\(u,v\)的距離是\(d_u,d_v\),\(u,v\)距離\(d\)
\(d_u+d\le d_v\)時,更新\(d_v=d_u+d\)
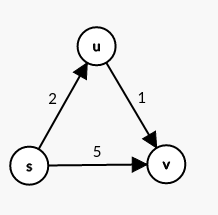
這時考慮用這條邊鬆弛
已經看過了這兩條邊
Bellman-Ford Algorithm
枚舉所有邊進行鬆弛,鬆弛 \(V-1\) 次
時間複雜度:\(O(VE)\)
為什麼\(V-1\)次一定可以?
因為一條簡單路徑最多只有\(V\)個點\(V-1\)條邊
#define pii pair<int,int>
vector<pii> G[N];
int dis[N];
//Bellman-Ford,起點1
fill(dis,dis+n+1,INF);
dis[1]=0;
for(int t=1;t<n;++t){
for(int u=1;u<=n;++u){
for(auto [v,d]:G[u]){
dis[v]=min(dis[v],dis[u]+d);
}
}
}優化版的Bellman-Ford aka SPFA
(Shortest Path Faster Algorithm)
每次只枚舉上次被鬆弛的點的邊
- 期望複雜度:\(O(V+E)\)
- 最差複雜度:\(O(VE)\)
實作
- 開一個queue存上次被鬆弛過的點
- 每次拿第一個出來鬆弛
- 把有鬆弛到的點加入queue
裸題
如果鬆弛V-1次後還能鬆弛就代表有一條V條邊的最短路徑
一定有負環
想不開的話可以用SPFA寫
還要更快?
如果沒有負邊的話...
最短路徑樹
子節點的距離一定不比父節點小
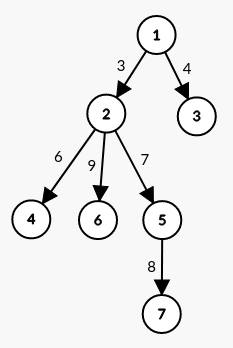
Dijkstra 戴克司tra
- 做一個最短路徑樹,原點到樹上每個點的最短距離都確定
- 每次找不在樹上、離原點最近的節點,原點到他的距離就確定了(因為不會有更近的路徑)
- 更新與他相鄰的點到原點的距離

實作方法
- 找離原點最近的點->用priority queue存到原點的距離
- pii存{到原點距離,index}
- priority_queue小的優先
priority_queue<pii,vector<pii>,greater<pii>>這裡如果放「小於」的話,pq會是從大到小
所以放「大於」就會從小到大
實作方法2
用struct存邊
要寫自定義的cmp,給priority queue用
好處是不用管pair的first跟second分別代表什麼
struct E{
int v,w;
};
vector<E> G[N];
struct cmp{
bool operator()(E a,E b){
return a.w>b.w;
}
};
priority_queue<E,vector<E>,cmp> pq;時間複雜度
把每條邊都push鬆弛一次、每個點pop一次
push pop都是\(O(log n)\)
\(n\)最多到\(E\)
\(O((E+V)log E)\)
優化
如果有鬆弛到才加入priority_queue
vector<E> G[N];//存邊
priority_queue<E,vector<E>,cmp> pq;//dijkstra
ll dis[N];
void Dijsktra(){
//init
fill(dis,dis+n+1,INF);
dis[1]=0;
pq.push({1,0});//到1的距離為0(起點
while(!pq.empty()){
E cur=pq.top();pq.pop();
if(dis[cur.v]<cur.w)continue;
for(auto [v,w]:G[cur.v]){
if(dis[v]>cur.w+w){
pq.push({v,cur.w+w});
dis[v]=cur.w+w;
}
}
}
}全點對最短距離
Floyd-Warshall
核心想法:每條路徑由起點、中繼點、終點構成
Floyd-Warshall
dp狀態
\(dp[k][i][j]\):利用前\(k\)個點當中繼點,\(i\)到\(j\)的最短距離
沒路過k 有路過k
dp轉移
\(dp[k][i][j]=min(dp[k-1][i][j],dp[k-1][i][k]+dp[k-1][k][j])\)
複雜度:\(O(V^3)\)
為什麼是對的?
如果能考慮到所有兩點間的路徑,就能找到最短路徑
i到j的路徑分為中繼點有0、沒有0
各自又分成有1、沒有1...於是包含了所有路徑
為什麼是對的?
如果能考慮到所有兩點間的路徑,就能找到最短路徑
i到j的路徑分為中繼點有0、沒有0
各自又分成有1、沒有1...於是包含了所有路徑
舉例
1
2
7
4
5
題目
DAG與拓樸排序
Directed Acyclic Graph 有向無環圖
DAG有向無環圖例子
什麼時候會用到
每個點代表一個狀態
有向邊代表可能的轉移方法
要找出一個順序,能夠把所有狀態一次算好
入度為0的代表結果已經確定,所以可以拔掉
並且更新他連出去的點的入度、狀態
實作
int deg[N];
vector<int> G[N],order;
queue<int> Q;
void topological_sort(){
memset(deg,0,sizeof(deg));
for(int i=0;i<n;++i){
for(int j:G[i])++deg[j];
}
for(int i=0;i<n;++i){
if(deg[i]==0)Q.push(i);
}
while(!Q.empty()){
int cur=Q.front();//以下要拔掉cur,並更新連出去的點
Q.pop();
order.push_back(cur);
for(int nxt:G[cur]){
//cur轉移到nxt
if(--deg[nxt]==0)Q.push(nxt);
}
}
}可以拓樸排序完再DP
也可以邊拓樸排序邊DP
<---噁心寫法
並查集
DSU Disjoint Set Union
功能
-
快速的合併兩個集合
- 查詢一個元素所在的集合(代表元素)
圖論中的用途
-
快速的合併兩個連通塊
-
查詢一個點所在的連通塊(代表點)
作法
每個集合/連通塊當作一棵有根樹
根節點當作代表元素
如何找代表?
在樹上一直往上走,根節點就是代表
如何合併?
把其中一個樹的根節點隨便接在另外一棵樹上
1
3
2
4
作法
每個集合/連通塊當作一棵有根樹
根節點當作代表元素
如何找代表?
在樹上一直往上走,根節點就是代表
如何合併?
把其中一個樹的根節點隨便接在另外一棵樹上
1
3
2
4
實作
舉例:一開始每個點都獨立,一直合併
- 開一個點數大小的陣列,第i個代表i的上級,一開始都是i
- 查詢時一直往上走
- 合併時把任一棵樹的根的爸爸設為另一棵樹的樹根
int f[N];
void init(){
for(int i=1;i<=n;++i)f[i]=i;
}
int fa(int me){
if(f[me]==me)return me;
return fa(f[me]);
}
void join(int a,int b){
int A=fa(a),B=fa(b);
f[A]=B;
}優化
路徑壓縮:直接把阿公(祖先)當作爸爸
啟發式合併:把小集合合併到大的集合
- 大小
- 深度
- 秩
其實沒寫啟發式合併也還好
平均複雜度\(O(\alpha(n))\),可以當作常數
最差複雜度\(log n\)
int f[N],sz[N];
void init(){
for(int i=1;i<=n;++i)f[i]=i,sz[i]=1;
}
int fa(int me){
if(f[me]==me)return me;
f[me]=fa(f[me]);//路徑壓縮
return f[me];
}
void join(int a,int b){
int A=fa(a),B=fa(b);
if(sz[A]<sz[B]){
//A併到B
f[A]=B;
sz[A]+=sz[B];
}else{
//B併到A
f[B]=A;
sz[B]+=sz[A];
}
}扣(依大小啟發式合併)
2021 11 APCS P4(ZJ g598)
先做一次塗色,每次加點時...

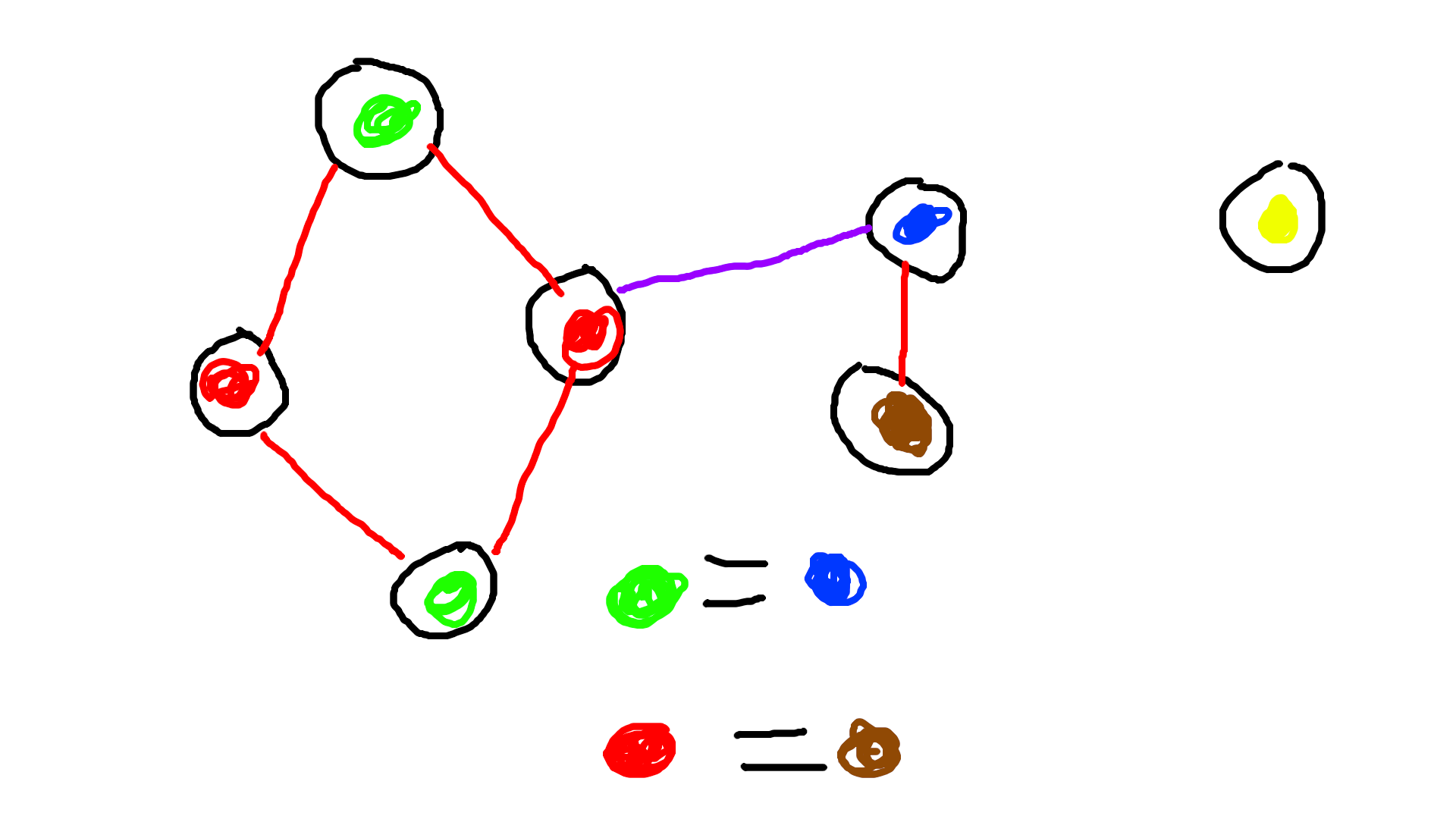

把每個顏色當成一個元素
加入新的邊u--v時
如果u,v的顏色在同一個集合就衝突了,否則
把(u的顏色)跟(v的同事的顏色)合併
把(v的顏色)跟(u的同事的顏色)合併
最小生成樹
MST Minimum Spanning Tree
定義
對於所有連通圖,點數與原圖相同、邊數最少的連通子圖
一定是一棵樹,稱為生成樹
邊權總和最小的生成樹即稱為最小生成樹
利用性質
一個連通圖內兩個未完成的最小生成樹
用最短的邊連接一定最好
Kruskal演算法
每次找當前權重最小的邊,
看端點是否在兩個不同的最小生成樹中,
是的話就把兩棵樹合併起來。
如何合併?
並查集
struct E{int u,v,w;};
bool cmp(E a,E b){return a.w<b.w;}
E edge[N];
int Kruskal(){
sort(edge, edge+m, cmp);
int ans=0;
for(int i=0;i<m;i++){
if(fa(edge[i].u)!=fa(edge[i].v)){
ans+=edge[i].w;
join(edge[i].u, edge[i].v);
}
}
return ans;
}Prim's Algorithm
跟Dijkstra類似
把「與原點距離」改成「與樹距離」
struct E{int v,w;};
struct cmp{bool operator()(E a,E b){return a.w>b.w;}};
priority_queue<E,vector<E>,cmp> pq;
pq.push({1,0});
int ans=0;
dis[1]=0;//到樹距離
while(!pq.empty()){
E cur=pq.top();pq.pop();
if(vis[cur.v])continue;
vis[cur.v]=1;
ans+=cur.w;
for(auto [v,w]:G[cur.v]){
if(!vis[v]&&dis[v]>w){
dis[v]=w;
pq.push({v,w});
}
}
}
題目:TIOJ 1211
裸題
圖論(一)(資讀)
By kennyfs
圖論(一)(資讀)
- 1,516



