Hidden Markov Model at a glance
Contents
- Markov Chain
- Hidden Markov Model
- 3 problems
- Sample with HMM
Markov Chain
Homogeneous Markov chain
Markov Chain
The second-order Markov chain
Markov Chain
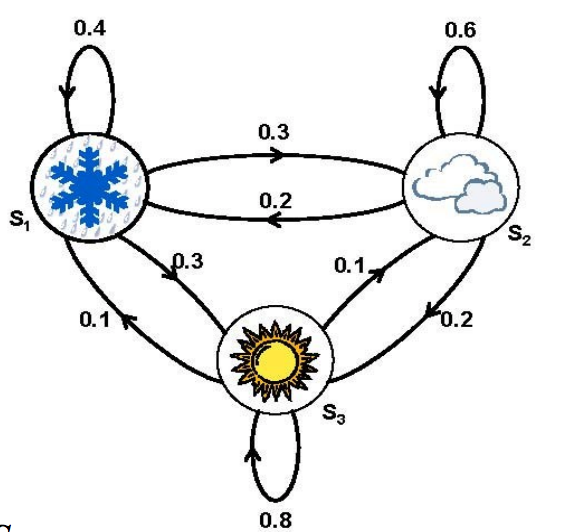
| rain | cloud | sun | |
|---|---|---|---|
| rain | 0.4 | 0.3 | 0.3 |
| cloud | 0.2 | 0.6 | 0.2 |
| sun | 0.1 | 0.1 | 0.8 |
HMM
HMM
HMM
Observed a data set
X = \{X_1,...,X_M\}
Latent vars
S = \{S_1,...,S_N\}
HMM params
\theta = \{\pi, A, B\}
A = \{a_{ij}\} \quad a_{ij} = P(z_t = S_j|z_{t-1}=S_i) \quad 1\leq i,j \leq N
B = \{b_{jk}\} \quad b_{jk} = P(x_t = X_k|z_{t}=S_j) \quad 1\leq j \leq N,1 \leq k \leq M
Three Problems
- Evaluation Problem
- Decode Problem
- Learning Problem
Evaluation Problem
Solve with Forward-Backward algorithm
Have observed
X=(x_1x_2...x_T)
and
\theta = \{\pi, A, B\}
evaluate
P(X|\theta)
Forward-Backward
idea
P(X|\theta) = \sum_Z{P(X,Z|\theta)} = \sum_Z{P(X|Z,\theta)}P(Z|\theta)
P(X|\theta) = \sum_{z_1,z_2,...,z_T} \pi_{z_1}b_{z_1X_1}a_{z_1z_2}b_{z_2X_2}...
with
\alpha_t(i) = P(x_1x_2...x_t, z_t = S_i|\theta)
=> \alpha_{t+1}(j)= b_{j x_{t+1}}\sum_{i=1}^N{\alpha_{t}(i)a_{ij}}
Forward
Backward
\beta_t(i) = P(x_{t+1}x_{t+2}...x_T,z_t=S_i|\theta)
Decode Problem
Have observed
X=(x_1,...,x_T)
and
\theta = \{\pi, A, B\}
find
Z^*=(z_1z_2...z_T)
that
Z^*= argmax P(Z|X, \theta)
http://www.utdallas.edu/~prr105020/biol6385/2018/lecture/Viterbi_handout.pdf
Learning Problem
Given a HMM θ, and an observation history
X = ( x_1x_2 ... x_T )
find new θ that explains the observations at least as well, or possibly better
P(X|\theta') \geq P(X|\theta)
Learning Problem
EM idea
Sample
Conclusion
deck
By Khanh Tran
