今井研・最終発表

阿部健信

目次

• 概要
• WL-Kernelの復習
• 手法
• 実験結果
• 考察・今後の課題

目次

• 概要
• WL-Kernelの復習
• 手法
• 実験結果
• 考察・今後の課題

概要

"Weisfeiler-Lehman Graph Kernels" JMLR 12 (2011) 2539-2561

のグラフカーネルフレームワークをコミュニティ検出に応用することを試みた。

具体的には、Planted CliqueとRandom Graphの分類問題に適用した。

目次

• 概要
• WL-Kernelの復習
• 手法
• 実験結果
• 考察・今後の課題

定義確認

• ノードにラベルのついた無向グラフを考える。
• グラフ \(G = (V, E, l)\)
• \(V\) : 頂点  (\(|V| = n\))
• \(E\) : 辺  (\(|E| = m\))
• \(l: V \to \Sigma\)  (\(\Sigma\)はアルファベット)
• \(\mathcal{N}(v) = \{v' \| (v, v') \in E \}\)
• (\(m > n\)を暗黙的に仮定している？)

論文の目的

• グラフの類似性判定は重要

ex. 化学物質の構造をグラフで表す。

→似た構造を持つ物質は同じ性質を持つ可能性が高いと考えられる。

グラフの類似性判定

• 同型判定 (同じサイズのグラフ)

NPであるが、NP困難であるかどうかもPであるかどうかもわかっていない。

• 部分グラフ同型判定 (違うサイズのグラフ)

NP困難であることが証明されている。

• 同型を用いた判定は、計算量が起きすぎることに加えて、自由度が少なく使いづらい。

WL Test of Isomorphism

• ラベル付き無向グラフG, G'の同型判定。
• 次のアルゴリズムに従って、ノードのラベルを更新していく。
• G, G'の頂点ラベルの集合が異なるもしくは、回数がn回に達するまでイテレーション。
• ラベルの集合が異なった場合は同型でない、全て同じ場合はほぼ全ての場合について同型である。

アルゴリズム

http://www.jmlr.org/papers/volume12/shervashidze11a/shervashidze11a.pdf

実行例

http://www.jmlr.org/papers/volume12/shervashidze11a/shervashidze11a.pdf

WL Sequence

• Weisfeiler-Lehman graph : \(G_{i} = (V, E, l_{i})\)
• the sequence of Weisfeiler-Lehman graphs :

$$ {G_{0}, G_{1}, ..., G_{h}} $$

WL Kernel

• \(k^{(h)}_{WL}(G, G') = k(G_{0}, G'_{0}) + k(G_{1}, G'_{1}) + ... + k(G_{h}, G'_{h})\)
• \(k\)が半正定値のカーネルであるとき、\(k^{(h)}_{WL}\)も半正定値になる。

WL Subtree Kernel

 $$ \phi^{(h)}_{WLsubtree}(G) = (c_{0}(G, \sigma_{01}), ..., c_{0}(G, \sigma_{0|\Sigma_{0}|}), ..., c_{h}(G, \sigma_{h|\Sigma_{h}|})) $$

• \(k(G, G') = \sum_{v \in V} \sum_{v' \in V'} \delta(l(v), l(v'))\)

     とすると、

 $$ (k^{(h)}_{WL}(G, G') = k^{(h)}_{WLsubtree}(G, G') $$

目次

• 概要
• WL-Kernelの復習
• 手法
• 実験結果
• 考察・今後の課題

実験内容

• Random GraphとPlanted Cliqueの分類問題の精度を測定した。
• Random Graph
  • \(p=1/2\)の確率で辺を貼ったグラフ
• Planted Clique
  • Random Graphに対して、\(\beta * \sqrt{n}\)頂点をcliqueにしたもの

工夫

• WL-Kernelは元々の論文では、頂点にラベル付きのグラフについてのアルゴリズムを提案していた。
• 今回は、ラベルなしのグラフを考えるため、以下の二つの条件でWL Subtree Kernelの応用を試みた。
  • \(l_0\)を全て同じ値で初期化
  • \(l_0\)を頂点の次数で初期化

実験手法

• 頂点数 \(n=100\)
• グラフ数 \(N=1000\)
  • Planted Clique, Random Graph半分ずつ
  • 学習用データ、テスト用データ半分ずつ
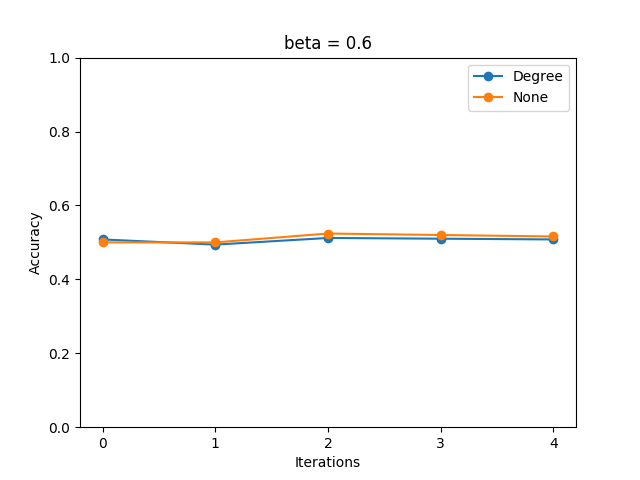
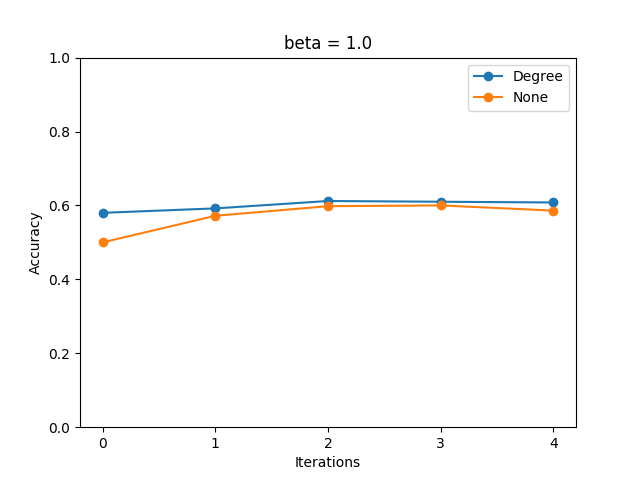
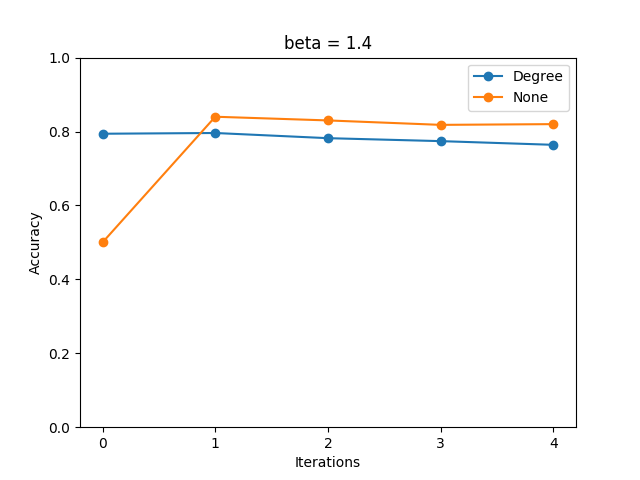
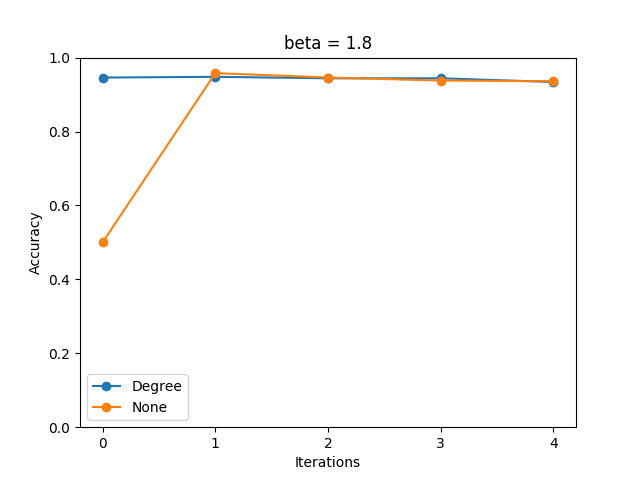
• \(\beta=0.6, 1.0, 1.4, 1.8\) について計測を行った。 
• 学習手法は線形SVMを利用

https://github.com/bknshn/WL-Kernel

目次

• 概要
• WL-Kernelの復習
• 手法
• 実験結果
• 考察・今後の課題

Title Text

• Bullet One
• Bullet Two
• Bullet Three

Title Text

• Bullet One
• Bullet Two
• Bullet Three

Title Text

• Bullet One
• Bullet Two
• Bullet Three

Title Text

• Bullet One
• Bullet Two
• Bullet Three

目次

• 概要
• WL-Kernelの復習
• 手法
• 実験結果
• 考察・今後の課題

考察

• イテレーション回数が1-3と小さめの値で収束が見られた。
• WL Subtree Kernelにおいては、ラベルを次数で初期化した場合、全て同じラベルで初期化したものの1イテレーションを回したものと等価である。

今後の課題

• ラベルの初期化の他の手段を試す。
• 他のbase kernelに適用して実験する。

終わりです。