Mathematical analysis of

data assimilation and

This talk

Data Assimilation (DA)

The seamless integration of data and models

Model

Dynamical systems and its numerical simulations

ODE, PDE, SDE,

Numerical analysis, HPC,

Fluid mechanics, Physics

chaos

error

Data

Obtained from experiments or measurements

Statistics, Data analysis,

Radiosonde/Radar/Satellite observation

noise

limited

×

\partial_t \bm{u} + (\bm{u} \cdot \nabla) \bm{u} = - \frac{1}{\rho} \nabla p + \nu \triangle \bm{u} + \bm{f}

Each has Uncertainty! (incomplete)

Data Assimilation (DA)

Control
- Nudging/Continuous Data Assimilation
Bayesian
- Particle Filter (PF)
- Ensemble Kalman filter (EnKF)
Variational
- Four-dimensional Variation method (4DVar)

Several formulations & algorithms of DA:

current study

→ next slide

Numerical Weather Prediction

typical application

Setup: Model

\frac{d u}{dt} = \mathcal{F}(u)

(\mathcal{F}: \mathcal{U} \rightarrow \mathcal{U}, u(0) = u_0 \in \mathcal{U})

u(t) = \Psi_t (u_0)

Model dynamics in

Semi-group in

\mathcal{U}

generates

\mathcal{U}

(\Psi_t : \mathcal{U} \rightarrow \mathcal{U}, t \ge 0)

(assume)

: separable Hilbert space

: separable Hilbert space (state space)

The known model generates

the unknown true chaotic orbit.

A small perturbation can

grow exponentially fast.

unknown orbit

Setup: Observation

Discrete-time model (at obs. time)

\mathcal{U}

(\Psi = \Psi_h, h > 0 \text{: observation interval})

We have noisy observations in

y_j = H u_j + \xi_j, \quad j \in \mathbb{N}.

(H: \mathcal{L}(\mathcal{U}, \mathcal{Y}), \xi_j \in \mathcal{Y} \text{ noise})

Noisy observation

u_j = \Psi(u_{j-1})

observe

u_1

y_1

u_2

y_2

t_1

t_2

t_3

...

bounded linear

\in \mathcal{Y}

\mathcal{Y}

(another Hilbert space).

\in \mathcal{Y}

Aim of Data Assimilation

u_j \in \mathcal{U}

Unkown state

Given obs.

Y_j = \{y_i \mid i \le j\} \subset \mathcal{Y}

v_j

Construct

u_j

estimate

Quality Assessment

\mathbb{E}\left[|v_j - u_j|^2\right]

y_j

\mathcal{U}

\mathcal{Y}

u_{j-1}

u_j

y_{j-1}

Given

Model

Obs.

unknown

(|\cdot|: \text{ norm of } \mathcal{U}, \mathbb{E}: \text{ expectation})

(\text{for } j \in \mathbb{N})

(filtering problem)

Bayesian Data Assimilation

\mathbb{P}^{v_{j-1}}

\mathbb{P}^{\hat{v}_j}

\mathbb{P}^{v_j}

(I) Prediction

by Bayes' rule

by model

(II) Analysis

y_j

We can compute it iteratively (2 steps at each time step).

Prediction

...

(\Rightarrow \mathbb{P}^{v_j} = \mathbb{P}^{u_j}({}\cdot{} | Y_j))

\mathcal{U}

y_1

t_1

t_2

t_3

t_0

(I) Prediction

\Psi

(II)Analysis

\mathbb{P}^{u_j}({}\cdot{} | Y_j)

Y_j = \{y_i \mid i \le j\}: \text{ observations up to time } j.

Goal: compute the conditional distribution

y_2

Need approximations!

Repeat (I) & (II)

→ next slide

Two major implementations of EnKF:
- Perturbed Observation (PO): stochastic → sampling error
- Ensemble Transform Kalman Filter (ETKF): deterministic

Ensemble filters

\mathcal{U}

y_1

y_2

t_1

t_2

t_3

...

t_0

Repeat (I) & (II)

(II)Analysis

(I) Prediction

\Psi

v_0^{(1)}

v_0^{(m)}

v_0^{(2)}

\widehat{v}_1^{(1)}

v_1^{(1)}

\vdots

Particle Filter(PF)

→ full distribution

Ensemble Kalman filter (EnKF)

→ mean & Covariance

(Burgers+1998)

(Bishop+2001)

A set of state vectors

(m \rightarrow \infty)

Mathematical analysis of EnKF

Assumptions on model

(Reasonable)

Assumption on observation

(Strong)

We focus on finite-dimensional state spaces

(\mathcal{U} = \R^{N_u} \text{ for } N_u \in \mathbb{N})

(T.+2024) K. T. & T. Sakajo (accepted 2024), SIAM/ASA Journal on Uncertainty Quantification.

Assumptions for analysis

N_y = N_u, H = I_{N_u}, \xi \sim \mathcal{N}(0, r^2 I_{N_u})

Assumption (obs-1)

"full observation"

Strong!

\exist \rho > 0 \text{ s.t. } \forall u_0 \in B(\rho), \forall t > 0, u(t ; u_0) \in B(\rho).

\exist \beta > 0 \text{ s.t. } \forall u \in B(\rho), \forall v \in \mathbb{R}^{N_u}, \langle F(u) - F(v), u - v \rangle \le \beta |u - v|^2.

\exist \beta > 0 \text{ s.t. } \forall u, v \in B(\rho), |F(u) - F(v)| \le \beta | u - v|.

Assumption (model-1)

Assumption (model-2)

Assumption (model-2')

\forall u_0 \in \R^{N_u}, \dot{u}(t) = F(u(t)) \text{ has an unique solution, and}

Reasonable

(B(\rho) = \{u \in \R^{N_u} \mid |u| \le \rho \})

"one-sided Lipschitz"

"Lipschitz"

"bounded"

Dissipative dynamical systems

Dissipative dynamical systems

Lorenz 63, 96 equations, widely used in geophysics,

\frac{du^i}{dt} = (u^{i+1} - u^{i-2}) u^{i-1} - u^i + f \quad (i = 1, \dots, N_u),

Example (Lorenz 96)

\bm{u} = (u^i)_{i=1}^{N_u} \in \mathbb{R}^{N_u}, f \in \R,

non-linear conserving

linear dissipating

forcing

Assumptions (model-1, 2, 2')

hold

incompressible 2D Navier-Stokes equations (2D-NSE) in infinite-dim. setting

Lorenz 63 eq. can be written in the same form.

→ We can discuss ODE and PDE in a unified framework.

can be generalized

\frac{du}{dt} =

B(u, u)

A u

bilinear operator

linear operator

dissipative dynamical systems

Mimics chaotic variation of

physical quantities at equal latitudes.

(Lorenz1996) (Lorenz+1998)

Dissipative dynamical systems

The orbits of the Lorenz 63 equation.

Literature review: analysis of EnKF

H = I_{N_u}

Error analysis for dissipative dynamical systems

Full observation ( )
- PO + add. inflation (Kelly+2014)
- ETKF + multi. inflation (T.+2024)
Partial observation → future

asmp obs1

asmp model1

asmp model2

asmp model2'

How EnKF approximate

the true state?

\mathbb{E}|error|^2 \le O(r_{obs}^2).

→ current

Consistency (Mandel+2011, Kwiatkowski+2015)
Sampling errors (Al-Ghattas+2024)

How EnKF approximate KF?

\mu^{m}_j, C^{m}_j \rightarrow \mu_j, C_j

Analysis for linear-Gaussian systems

Error analysis of ETKF (our)

\text{Let } e_j =\overline{v}_j - u_j\text{ where } \overline{v}_j = \frac{1}{m} \sum_{k=1}^m v^{(k)}_j.

\text{Let us consider the ETKF with multiplicative inflation } \alpha \ge 1.

(T.+2024) K. T. & T. Sakajo (accepted 2024), SIAM/ASA Journal on Uncertainty Quantification.

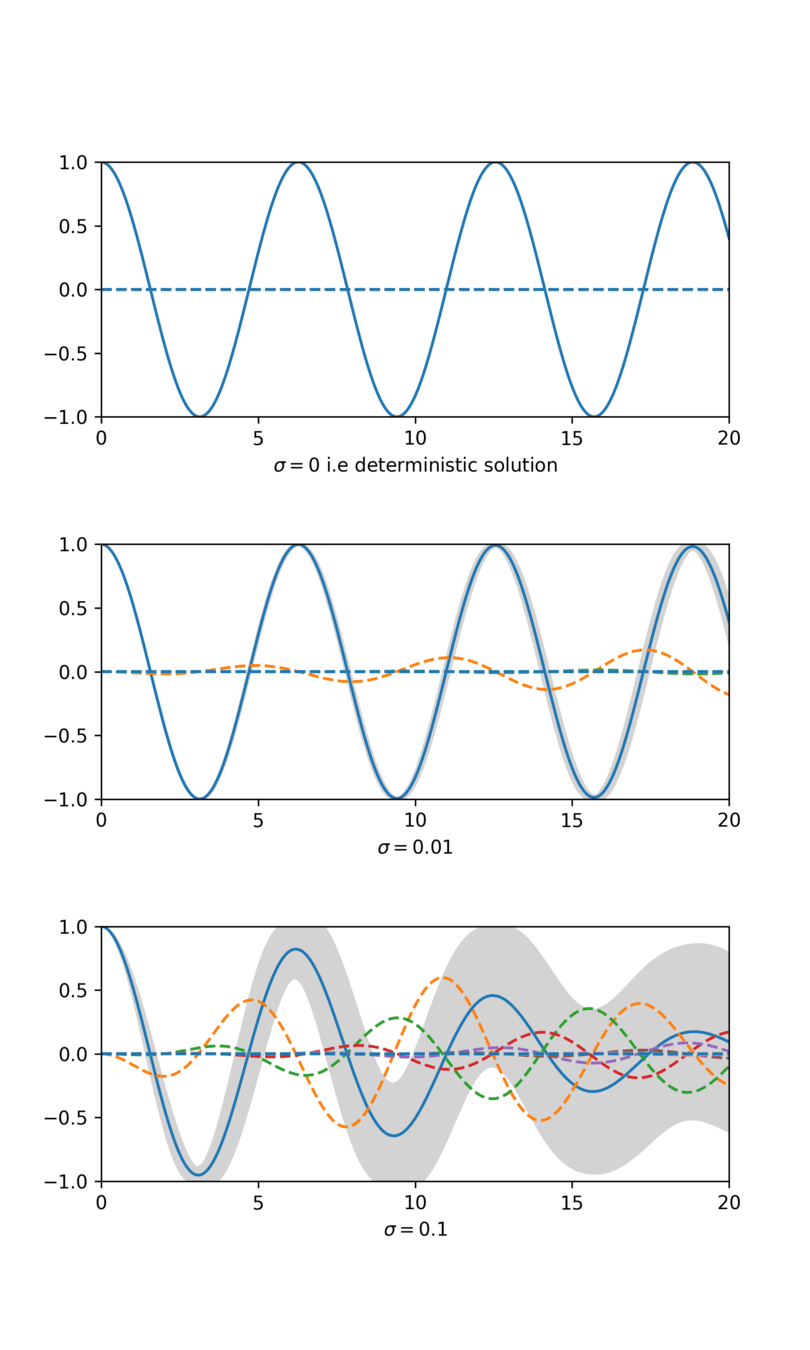
\limsup_{j \rightarrow \infty} \mathbb{E}[|e_j|^2] \le \frac{N_u r^2}{1-\theta} + \left(\frac{1 - \Theta}{1 - \theta} - 1\right)D.

Theorem 2 (T.+2024)

\text{where } \Theta = \Theta(\beta, \rho, h, r, m, \alpha) , D = D(\beta, \rho) > 0.

\text{Then, } \exist \theta = \theta(\beta, \rho, h, r, m, \alpha) < 1\text{ s.t.}

\text{Let Assumptions (obs-1, model-1,2') hold.}

\text{Suppose } m > N_u, \operatorname{rank}(C_0) = N_u,\alpha \gg 1, \text{ and}

v_j^{(k)} \in B(\rho) \text{ for } k = 1, \dots, m \text{ and } j \in \N.

Sketch: Error analysis of ETKF

< e^{-\beta h}

= \frac{1}{1 + \alpha^2 r^{-2} \lambda_{min}(\widehat{C}_j)}

①

②

Key result

\because

(1) \text{ We establish a lower bound of eigenvalues of } \widehat{C}_j \text{ by } \alpha \gg 1.

(2) \text{ If } \widehat{C}_j \text{ is positive-difinite, we have a bound by } \alpha \gg 1.

Data Assimilation (DA)

Control
- Nudging/Continuous Data Assimilation
Bayesian
- Particle Filter (PF)
- Ensemble Kalman filter (EnKF)
- Quantum DA
Variational
- Four-dimensional Variation method (4DVar)

PDE

Optimal Transport

Metrics

Machine

Learning

Diffusion model

Back Prop.

Supervised Learning

Lyapunov

analysis

Signature

Wasserstein

Operator

Algebra

Koopman operator

Optimization

Dynamical system

Numerical Analysis

structure-preserving

Numerical error

SDE

Dynamics

Uncertainty Quantification

Probability/Statistics

& related topic

Stochastic Galerkin

Random ODE

Other formulations

Control formulation

Problem

Keywords/Mathematics

(Olson+2003), (Azouani+2011)

Nudging/Continuous Data Assimilation

Squeezing property, Determining mode/node

AOT-algorithm

\frac{du}{dt} = \mathcal{F}(u),

v = \mathcal{P} u + q, \quad \frac{dq}{dt} = (I - \mathcal{P})\mathcal{F}(v).

If we have noiseless & continuous time observations

through an orthogonal projection

→ copy obs. to the simulated state

(true)

(simulate)

\mathcal{P}: \mathcal{U} \rightarrow \mathcal{Y}.

\text{Estimate the smallest rank of } \mathcal{P} \text{ s.t.}

\lim_{t \rightarrow \infty}|v(t) -u(t)| \rightarrow 0.

PDE (Partial Differential Equations)

Control theory/Synchronization

Incomplete atmospheric data

(Charney+1969)

u = \sum_{|k| \le \lambda} u_k \phi_k + \sum_{|k| >\lambda} u_k \phi_k

v = \sum_{|k| \le \lambda} u_k\phi_k + \sum_{|k| >\lambda} v_k \phi_k

\mathcal{P}_{\lambda} u

copy

converge

(t\rightarrow\infty)

\lambda > 0: \text{ threshold for wavelength}

Variational formulation

Problem

Keywords/Mathematics

(Law+2015), (Korn+2009)

4DVar

Adjoint method to compute gradient

Optimization, Iteration method

\text{Well-posedness of a mininization problem}

v_0 = \argmin_{u_0} J(u_0; \theta)

To estimate the initial state

from observation data

y_1, \cdots, y_J \in \mathcal{Y}

J(u_0;\theta) = \sum_{j=1}^J \|R^{-1/2} (y_j - H(\Psi_{hj}(u_0;\theta)))\|^2

u_0 \in \mathcal{U}

minimize a cost function.

\nabla_{u_0} J(u_0)

u_0

y_1

y_2

y_3

y_4

Supervised Learning

(\theta: \text{ model parameters})

\widehat{\theta} = \argmin_{\theta} J(u_0; \theta)

Back propagation

DA & Numerical Analysis

Discretization/Model errors

Motivation

- Including discretization errors in the error analysis.

- Consider more general model errors and ML models.

- Error analysis with ML/surrogate models.

(Reich+2015)

Question

- Can we introduce the errors as random noises in models?

- Can minor modifications to the existing error analysis work?

\widetilde{\Psi}_t(x) = \Psi_t(x) + \xi_t ?

Math: Numerical analysis, UQ

Dimension-reduction for dissipative dynamics

Motivation

- Defining "essential dimension" and relaxing the condition:

- should be independent of discretization.

(Tokman+2013)

N_{ess} \le N_u

m > N_u \rightarrow m > N_{ess}

N_{ess}

Question

- Dissipativeness, dimension of the attractor？

- Does the dimension depend on time and state? (hetero chaos)

- Related to the SVD and the low-rank approximation?

Attractor

Math: Dynamical system

Numerics for UQ

Motivation

- Computing the Lyapunov spectrum of atmospheric models.

- Estimating unstable modes (e.g., singular vectors of Jacobian).

(Bridges+2001) (Ginelli+2007) (Saiki+2010)

Question

- Can we approximate them only using ensemble simulations?

- Can we estimate their approximation errors?

Math: Lyapunov analysis, Numerical analysis

Imbalance problems

Motivation

- Assimilating observations can break the balance relations inherited from dynamics. → numerical divergence

(e.g., geostrophic balance and gravity waves）

- Explaining the mechanism (sparsity or noise of observations?).

- Only ad hoc remedies (Initialization, IAU).

(Kalney 2003), (Hastermann+2021)

Question

- Need to define a space of balanced states?

- Need to discuss the analysis state belonging to the space?

- Can we utilize structure-preserving schemes?

balanced states

Math: Structure-preserving scheme, constrained optimization

Stochastic Galerkin

Problem

Keywords/Mathematics

(Sullivan2015) (Janjić+2023)

Weak formulation, Galerkin method, Lax-Milgram,

Generalized Polynomial Chaos Expansions

Karhunen–Lo`eve Expansions

Spectral expansion for sample space.

Random Harmonic oscillator

(uncertain angular frequency)

U(t, \theta) = \sum_{k \in \mathbb{N}} u_k(t) \phi_k(\theta)

\theta (\omega) \sim N(0, 1),

\mathbb{E} [U(t)] = u_1(t),

\mathbb{V} [U(t)] = \sum_{k \in \mathbb{N}} u_k^2 \langle \phi_k^2 \rangle.

U(t, \omega)

Random field

is represented by

using a stochastic germ

and the associated polynomials

(\phi_k(\theta))_{k \in \mathbb{N}}.

We can compute cumulants using the coefs.

\ddot{U} = - \Omega U, U(0) = 1, \dot{U}(0) = 0.

\log \Omega \sim N(0, \sigma^2).

Quantum DA & Operator Algebra

Problem

Keywords/Mathematics

(Freeman+2023)

Koopman operator

Generalizing data assimilation by embedding it in a nonabelian operator algebra based on von Neuman algebra

\mathfrak{B} = B(H).

Quantum mechanics

Quantum computer

\mathfrak{A} = L^\infty(X, \mu).

(H = L^2(X, \mu))

S(\mathfrak{A}):

Observable

\pi: \mathfrak{A} \ni f \mapsto \pi f \in \mathfrak{B},

Embedding

(\pi f) g = fg \in H, \ \forall g \in H.

State

(Giannakis+2019)

continuous linear positive functionals on

\mathfrak{A}.

Metrics on DA

Problem

Keywords/Mathematics

(T.+2024)

Persistent Homology

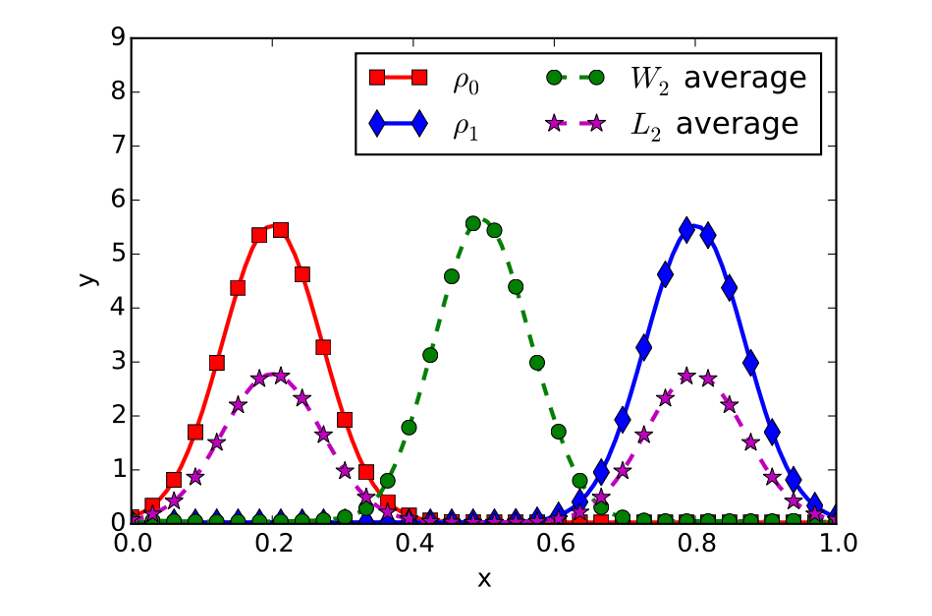
In the variational formulation, the analysis state can be understood as the barycenter of the prediction and observation.

(N. Feyeux et al. 2018)

Signature / Rough path

Wasserstein / OT

v = \argmin_u d_1(u, \widehat{v})^2 + d_2(Hu, y)^2.

(Clausel+2024)

(N. Feyeux et al. 2018)

Different ways to define a barycenter.

Limitation of the Euclid average.

\text{where } d_1, d_2 \text{: distance-like functions.}

PF & Optimal Transport

Problem

Keywords/Mathematics

(Reich2013)

Optimal Transport, Sinkhorn algorithm

Monge-Kantorovich, Benamou-Brenier

\widehat{u}^{(1)}

prior

posterior

Aim: obtain equal-weighted posterior samples

Gradient flow

Mean-field, Fokker-Planck

Diffusion model

Schrödinger bridge

stochastic-ver.

\mathcal{Z} = \{\hat{u}_1, \dots, \hat{u}_m\}

Prior samples

Seek a coupling

between two discrete random variables

Z^a: \Omega \rightarrow \mathcal{Z}

Z^f: \Omega \rightarrow \mathcal{Z}

p^f = (1/m, \dots, 1/m)^T

p^a = (w_1, \dots, w_m)^T

T \in \mathbb{R}^{m \times m}

t_{ij} = (T)_{ij} \ge 0.

\sum_{i=1}^m t_{ij} = 1/m, \quad \sum_{j=1}^m t_{ij} = w_i

\widehat{u}^{(m)}

\min_T \mathbb{E}_{Z^f, Z^a}[d(z^f, z^a)] = \min_T \sum_{i, j}^m t_{ij} d(x^f_i, x^f_j).

\vdots

u^{(1)}

u^{(m)}

\vdots

(Jarrah+2023)

(Reich2019)

Topic

Problem/Question

Goal

Mathematics/Fields

Figure

refs

Mathematical analysis of data assimilation and related topics

By kotatakeda

Mathematical analysis of data assimilation and related topics

Applied Mathematics Freshman Seminar 2024 Kyoto