The Knowledge Base Paradigm
for
Decision Management
Decision Representation
- Business Rules
- Decision Tables
Business Processes-
DMN
- Decision Tables
- FEEL
- Logic
Declarative
Problem Solving
- Deductive logic – deduction
- Query languages (SQL, datalog) – query answering
- Constraint programming – constraint solving
- Logic Programming – programming
- Abductive Logic Programming – abduction
- Inductive Logic Programming - induction
- PDDL, strips – planning
- Answer set programming – model generation
Declarative
Problem Solving
Focus on a single specific form of inference
=> One representation, one problem
Knowledge Base
Paradigm
Information
≠ Solution
≠ Problem description
= Passive, independent of specific problem
=> One representation, many problems
Knowledge Base
Paradigm
FO(.)
- IDP's Representation Language
- Extension of first-order logic:
- Types
- Arithmetic
- Aggregates
- Inductive definitions
- ...
- Formal Model Semantics
- Extension of first-order logic:
Decision Logic
+
Decision
Specification
+
Inference
Decision Management
Knowledge Base Paradigm
Modelling Business Decisions
An Example
Car Insurance
DMN - DRD
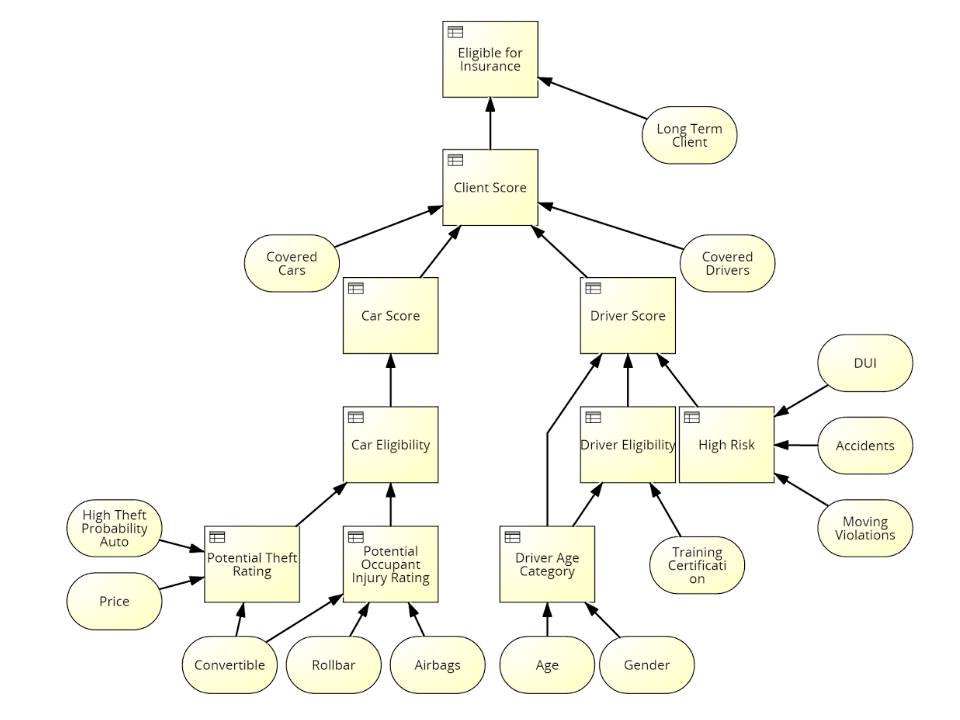
Potential Theft Rating
-
A car's theft rating is high if any of the following applies:
- The car is a convertible
- The car's price is over $45 000
- The car's model is on the High Theft Probability Auto list
-
If all of the following are true the car's theft rating is moderate:
- The car's price is between $20 000 and $45 000
- The car's model is not on the High Theft Probability Auto list
-
If all the following are true the car's theft rating if low:
- The car's price is lower than $20 000
- The car's model is not on the High Theft Probability Auto list
Decision Table
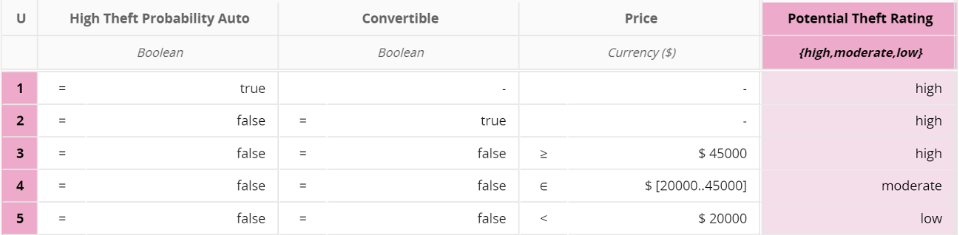
Potential Theft Rating
Definition
Potential Theft Rating
FO(ID) Definitions
A definition ∆ of the logic FO(ID) is a set of definitional rules: ∀ x : (P(t) ← ϕ) where ϕ is a FO-formula and t a tuple of n-terms, both with free variables amongst x.
Decision Logic in FO(ID)
A decision's decision logic* in FO(ID) is a set of rules:
∀ x : (P(t) ← ϕ) where ϕ is a FO-formula and t a tuple of n-terms, both with free variables amongst x.
* for decisions representable by a decision table
Decision Table
Functionality
- Completeness checking
- Exclusivity checking
- Invokation
Decision Logic Definition
Functionality
- Completeness checking
- Exclusivity checking
- Compliance checking
- Invokation
{
counter examples
Complete Input
Incomplete Input
Alternatives
Completeness*
At least one outcome for every input value assignment
Violated if:
There exists a value assignment for which there is no outcome.
Exclusiveness*
At most one outcome for every input value assignment
Violated if:
There exists a value assignment for which there is more than one outcome.
\exists \bar{X} : \neg \exists \bar{Y} : P(\bar{X}, \bar{Y})
* Weak forms of completeness & exclusiveness
\exists \bar{X} : \exists_{>1} \bar{Y} : P(\bar{X}, \bar{Y})
Stronger
Requires quantification over rules
=> rule reification
Compliance
Check whether the decision logic satisfies a certain property
"Minors can not be insured as drivers"
Violated if:
It is possible for someone younger than 18, to be insured.
\exists c ~ d : Covers(c, d) \wedge
DriverAge(d) < 18 \wedge EligibleForInsurance(c, eligible)
Invokation
- Invoke decision with
- all input values available
- some input values available
- Determine input alternaties for desired outcome
Decisions
By krr
