Proof Theory

Historical Perspective and Current Research

 

DTAI seminars

Jo Devriendt

Contents ...

Disclaimer ...

 

What is a proof?

  • List of true axioms
  • List of inferred lemma's
    • Contains statement to be proven

Informally

  • Axiom: All men are mortal
  • Axiom: Socrates is a man
    • Inferred lemma: Socrates is mortal

What is a proof?

In this presentation:
propositional refutation

  • Propositional theory T
  • Derived propositions φ
    • Inconsistent proposition (⊥ or 0 ≥ 1 or 1=0)
a \Rightarrow b
a⇒ba \Rightarrow b
\neg c
¬c\neg c
a
aa
b \Rightarrow c
b⇒cb \Rightarrow c
b
bb
\bot
⊥\bot
c
cc

What is a proof system?

  • Language to write statements
  • Syntactical inference rules

Informally

  • Propositional clauses

     
  • Resolution rule
\frac{C \vee p \;\;\;\; D \vee \neg p}{C \vee D}
C∨pD∨¬pC∨D\frac{C \vee p \;\;\;\; D \vee \neg p}{C \vee D}
C = a \vee \neg b \vee c
C=a∨¬b∨cC = a \vee \neg b \vee c

Resolution proof system

Resolution proof system

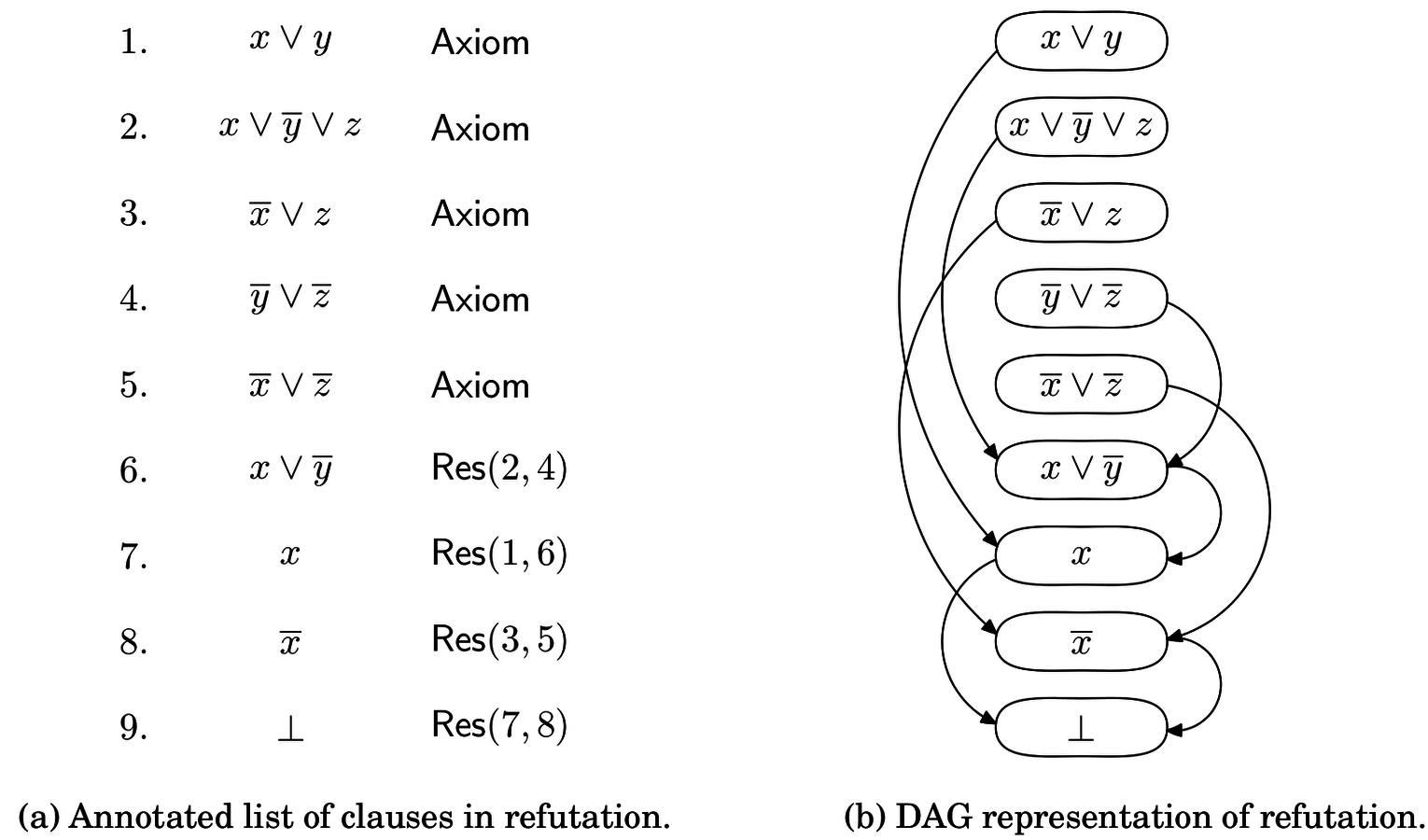
Extended resolution proof system

  • Resolution:



     
  • Variable introduction:
\frac{C \vee p \;\;\;\; D \vee \neg p}{C \vee D}
C∨pD∨¬pC∨D\frac{C \vee p \;\;\;\; D \vee \neg p}{C \vee D}
\frac{}{\neg p \vee C \;\;\;\; \forall l \in C:\; \neg l \vee p}
¬p∨C∀l∈C:¬l∨p\frac{}{\neg p \vee C \;\;\;\; \forall l \in C:\; \neg l \vee p}

Cutting plane proof system

  • Linear inequalities:

     
  • Inference rules:
a_1x_1+a_2x_2+a_3x_3 \geq A \;\;\;\; a_i,A \in \mathbb{Z}, x_i \mapsto \mathbb{Z}
a1x1+a2x2+a3x3≥Aai,A∈Z,xi↦Za_1x_1+a_2x_2+a_3x_3 \geq A \;\;\;\; a_i,A \in \mathbb{Z}, x_i \mapsto \mathbb{Z}

Cutting plane proof system

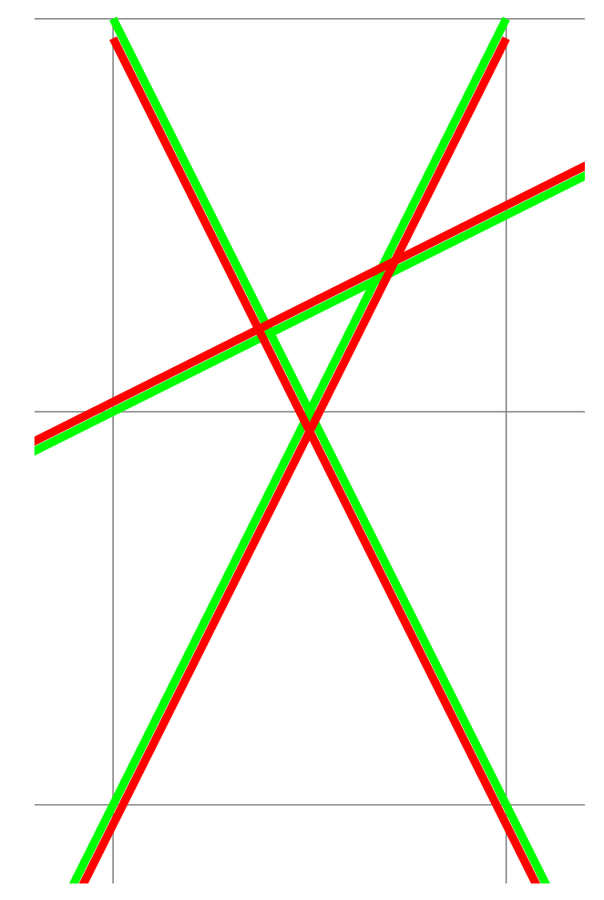
  1.     -2x +    y ≥ 0     (axiom)
  2.        x + -2y ≥ -2    (axiom)
  3.      2x +    y ≥ 2      (axiom)
  4.      2x + -4y ≥ -4    (2*2)
  5.              -3y ≥ -4    (1+4)
  6.                -y ≥ -1    (rounding of 5)
  7.      2x          ≥ 1     (3+6)
  8.        x          ≥ 1     (rounding of 7)
  9.     -2x          ≥ -1    (1+6)
  10.       -x          ≥ 0     (rounding of 9)
  11.                 0 ≥ 1     (8+10)

Polynomial calculus proof system

  • Polynomials:

     
  • Inference rules:
x\bar{y}+z=0 \;\;\;\; x,\bar{y},z \mapsto \mathbb{F}
xy¯+z=0x,y¯,z↦Fx\bar{y}+z=0 \;\;\;\; x,\bar{y},z \mapsto \mathbb{F}

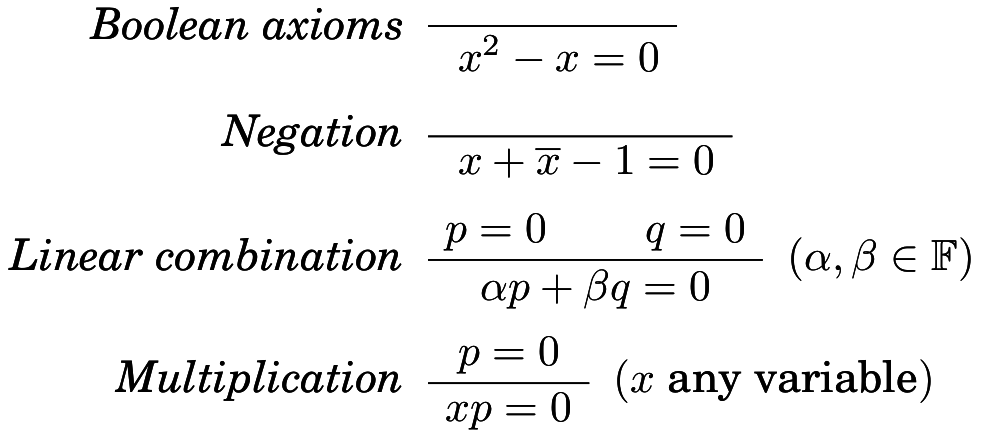
Polynomial calculus proof system

Propositional context:

  •     = GF(2)
  • true = 0
  • false = 1
  •                                                 
  • Derive 1=0
\mathbb{F}
F\mathbb{F}
x \vee \neg y \vee z \; \leftrightarrow \; x\bar{y}z=0
x∨¬y∨z↔xy¯z=0x \vee \neg y \vee z \; \leftrightarrow \; x\bar{y}z=0

Comparison of proof systems (1)

  • proof system A p-simulates proof system B
    iff there exists a polytime algorithm transforming B-proofs in A-proofs
    • A ≥ B
    • A "is at least as strong as" B
  • RES ≤ CUTPLANE ≤ ERES
  • RES ≤ POLYCALC

RES ≤ CUTPLANE

\frac{x + (1-y) + z \geq 1 \;\;\;\; (1-y)+(1-z)\geq 1}{x+(2-2y)\geq 2}
x+(1−y)+z≥1(1−y)+(1−z)≥1x+(2−2y)≥2\frac{x + (1-y) + z \geq 1 \;\;\;\; (1-y)+(1-z)\geq 1}{x+(2-2y)\geq 2}
x \geq 0
x≥0x \geq 0
\frac{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}{2x+(2-2y)\geq 2}
2x+(2−2y)≥2\frac{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}{2x+(2-2y)\geq 2}
\frac{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}{x+(1-y)\geq 1}
x+(1−y)≥1\frac{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}{x+(1-y)\geq 1}

(b) Corresponding cutting plane derivation

RES ≤ POLYCALC

Comparison of proof systems (2)

  • Proof size: number of steps in proof
  • Lower bounds exist!
    • Pigeonhole formula
      • exponential lower bound - RES and POLYCALC
      • poly proof exists - CUTPLANE and ERES
    • Tseitin formula
      • exponential lower bound - RES
      • poly proof exists - POLYCALC and ERES

Comparison of proof systems (3)

  • RES < CUTPLANE ≤ ERES
  • RES < POLYCALC

Combinatorial solvers with "learning"

are

Proof generators

  • SAT, SMT, PB, CP
  • Lower bound on runtime complexity by lower bound on proof size!

What proofs are generated?

Conflict Driven Clause Learning

while(true){
  if(theory contains ⊥){
    return UNSAT
  }else if(model found){
    return SAT
  }
  branch
  (reasoned) propagate
  while(conflict){
    resolve conflict clause to learned clause
    backjump
    add learned clause to theory
    (reasoned) propagate
  }
}

Conflict Driven Clause Learning

CDCL "p-simulates" RES

  • Reason clause for each propagation
  • Conflict clause is unsat
    • can be resolved with reason clauses
    • constructs resolution proof

Where are the stronger proof systems?

  • Polynomial calculus
    • PolyBoRi
  • Cutting planes
    • IntSat
  • Extended resolution
    • GlucosER

IntSat

  • Solves integer program (set of "cutting planes")
  • Treats clauses as pseudoboolean cp
  • Reason cp
  • Learned cp derived from conflict cp
    • linear combinations
    • roundings

IntSat

  1. x + y - z ≥ 3      (theory)
  2. x + y + z ≥ 6     (theory)
  3. 2 ≥ y                 (branch)
  4. 2 ≥ x                 (branch)
  5. 1 ≥ z                 (propagation from 1)
  6. z ≥ 2                 (propagation from 2)
  7. CONFLICT!
  8. derive 2x+2y ≥ 9 (derived from 1+2)
  9. learn x+y ≥ 5       (rounded from 8)
  • Learned cp prevents conflicts!
  • Learned cp is stronger than x≥3 v y≥3
  • But...

IntSat

Problematic learned cp's

x+y+2z \leq 2
x+y+2z≤2x+y+2z \leq 2
y - 2z \leq 0
y−2z≤0y - 2z \leq 0
0 \leq x
0≤x0 \leq x
1 \leq y
1≤y1 \leq y
x+2y \leq 2
x+2y≤2x+2y \leq 2

Does not avoid conflict...

Conflict over z!

2z \leq 1
2z≤12z \leq 1
1 \leq 2z
1≤2z1 \leq 2z

(z is integer)

Proposed learned constraint:

Branching
choices

IntSat

  • Solves integer program (set of "cutting planes")
  • Treats clauses as pseudoboolean cp
  • Reason cp
  • Learned cp derived from conflict cp
    • linear combinations
    • roundings
  • Also backup CDCL!
    • Reason clause
    • Conflict clause
    • Learned clause
  • Forgets learned clause
    after backjump

IntSat

while(true){
  if(theory contains 0≥1){
    return UNSAT
  }else if(model found){
    return SAT
  }
  branch on variable bound
  (reasoned) propagate
  while(conflict){
    add learned cutting plane to theory
    resolve conflict clause to learned clause
    backjump on learned clause
    (reasoned) propagate
  }
}

Structure-based Extended Resolution in CP

  • Introduce partial sums for linear terms:


     
    • Only when needed ("lazy")
    • Connection to ERES!
  • Exploit bounds on partial sums in reason clauses
\sum_{0\leq i \leq n} a_ix_i = [\sum_{0\leq i \leq n-1} a_ix_i] + a_nx_n
∑0≤i≤naixi=[∑0≤i≤n−1aixi]+anxn\sum_{0\leq i \leq n} a_ix_i = [\sum_{0\leq i \leq n-1} a_ix_i] + a_nx_n

Structure-based Extended Resolution in CP

  • Adding [x+y] as a variable to the CP engine allows for shorter learned clauses.
    • ([x+y] ≥ 5) instead of (x≥3 v y≥3)
  • IntSat seems to generalize this!
  1. [x+y] - z ≥ 3      (theory)
  2. [x+y] + z ≥ 6     (theory)
  3. 2 ≥ x                  (branch)
  4. 2 ≥ y                  (branch)
  5. 1 ≥ z                  (propagation from 1)
  6. z ≥ 2                  (propagation from 2)
  7. CONFLICT!
  8. derive [x+y] ≥ 5 (from negation of 3 and 4)

IDP4: Maybe both?

while(true){
  if(theory contains 0≥1 or ⊥){
    return UNSAT
  }else if(model found){
    return SAT
  }
  branch on atom / variable bound
  (reasoned) propagate
  while(conflict){
    add learned cutting plane to theory
    add learned clause to theory
    backjump on strongest of learned clause 
        and learned cutting plane
    (reasoned) propagate
  }
}

Questions?

Thanks for your attention!

Literature references available upon request

On Proof Theory

By krr

Source: Jo Devriendt

On Proof Theory

DTAI presentation

  • 1,725

More from krr