Michael Küffmeier (Carlsberg reintegration fellow)
Modeling embedded disks with infall through streamers
Sigurd Jensen, Jaime Pineda, Paola Caselli (MPE), Christian G. Holm, Troels Haugbølle (NBI), Stefan Reißl, Kees Dullemond (ITA)
SU Aur
synthetic image
Let's go back in time to the year 2014
Wow!
Credit: ALMA (ESO/NAOJ/NRAO)
Credit:
DSHARP team
10 au
50 au
The classical picture
credit: M. Persson
star formation
planet formation
History of modeling disk formation
spherical core collapse:
rotation
magnetization (mass-to-flux ratio)
non-ideal MHD effects
dust evolution
turbulence
useful for parameter studies
\rho(r) = \frac{\rho_{\rm c} R_{\rm c}^2}{R_{\rm c}^2 + r^2}
Bonnor-Ebert sphere
or uniform density
\rho(r) = \rho_{0}
History of modeling disk formation
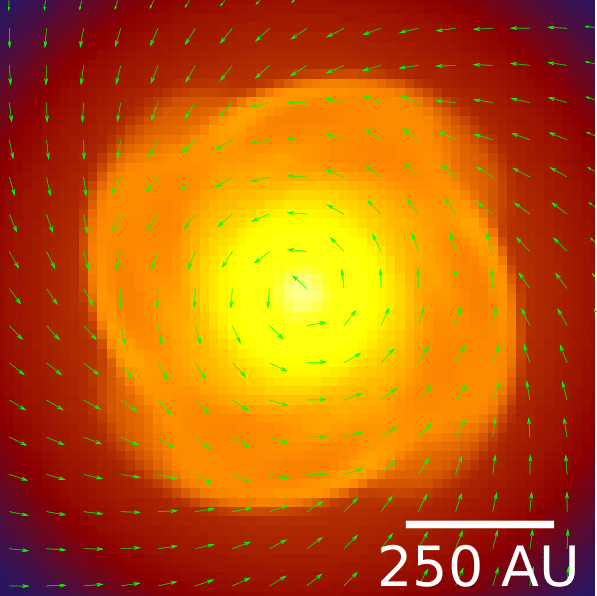
What about magnetic fields?
Help! Where is the disk?!
Santos-Lima et al. 2012
Hydro
ideal MHD
L_{\rm mag} = \int_{t_{\rm c}}^{t}\int^V r (\mathbf{J} \times \mathbf{B})_\phi \mathrm{d}V\mathrm{d}t
Magnetic braking catastrophe
Angular momentum is transported too efficiently away from the disk
magnetohydrodynamics
\frac{\partial \mathbf{B}}{\partial t} = \nabla\times (\mathbf{v}\times\mathbf{B})
ideal MHD
\color{red}-\nabla\times[\eta_{\rm O} (\nabla \times \mathbf{B})]
\color{purple}-\nabla\times \{\eta_{\rm H} [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}
\color{blue}-\nabla\times \{\eta_{\rm AD} \mathbf{B}/B \times [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}
Ohmic dissipation
Hall
ambipolar diffusion
Non-ideal
History of modeling disk formation
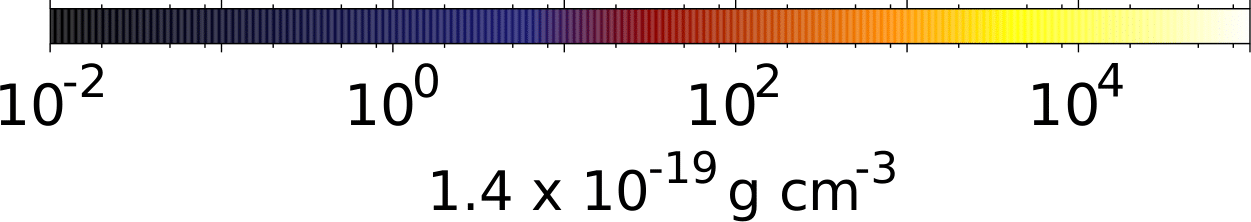
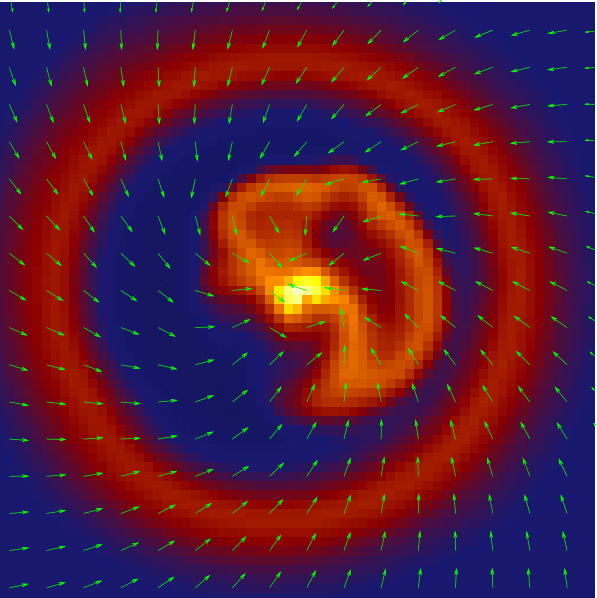
What about magnetic fields?
Help! Where is the disk?!
Ohmic, Ambipolar, Hall
Santos-Lima et al. 2012
Hydro
ideal MHD
non-ideal MHD
non-ideal MHD not a fixed parameter
すみません。
depends on cosmic-ray ionization rate
(Wurster et al. 2020, Kuffmeier et al. 2020, Kobayashi et al. 2023; talks by Marchand & Nishio)
for more references, see reviews (e.g., Wurster & Li 2018, Tsukamoto et al. 2023, Kuffmeier subm.); talks by Lee, Lebreuilly, Commercon, Harada, Bhandare and Xu
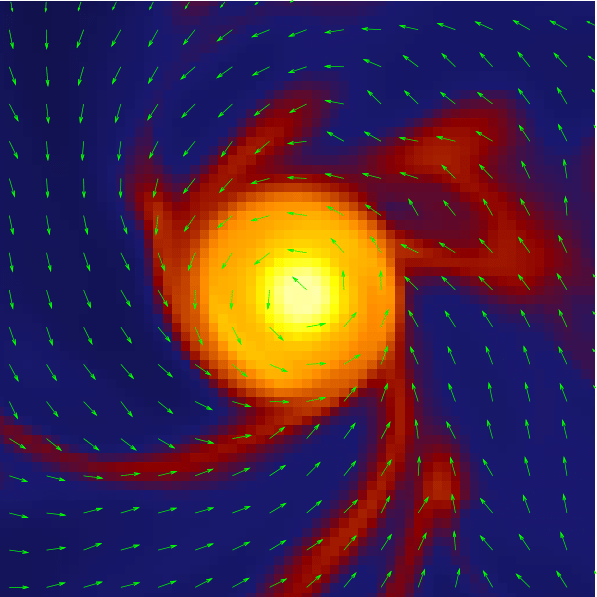
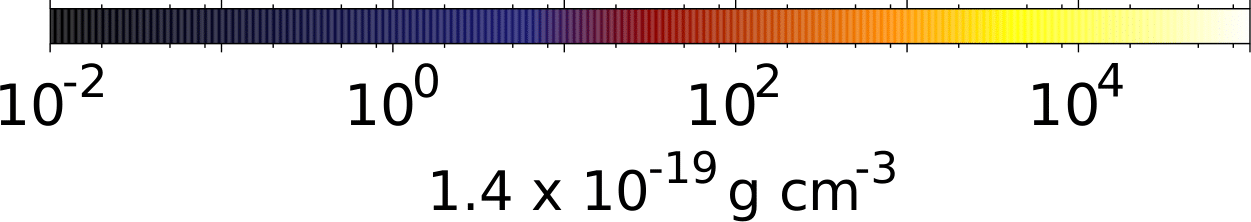
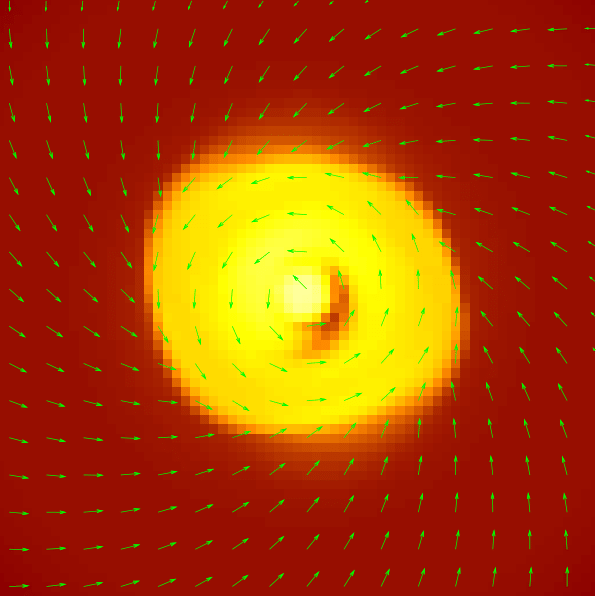
What about magnetic fields?
Help! Where is the disk?!
Ohmic, Ambipolar, Hall
Turbulence
Santos-Lima et al. 2012
Hydro
ideal MHD
non-ideal MHD
turbulence + MHD
Other effect: dust
dust growth weakens magnetic braking => larger disks
Zhao et al. 2018, Marchand et al. 2020
dust-rich disks from collapse
"ash-fall" scenario
Tsukamoto et al. 2021
Lebreuilly et al. 2020/203
dust accumulates
History of modeling disk formation
Is this the full picture?
Credit: ALMA (ESO/NAOJ/NRAO)
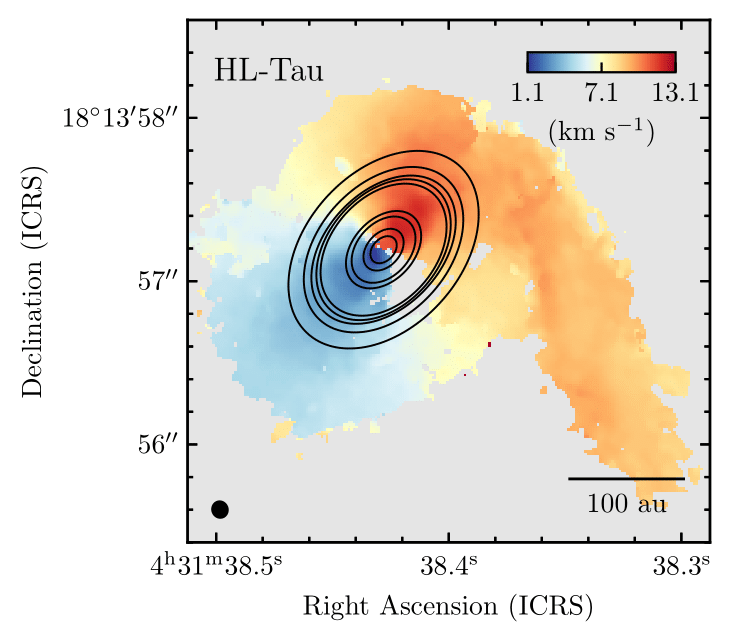
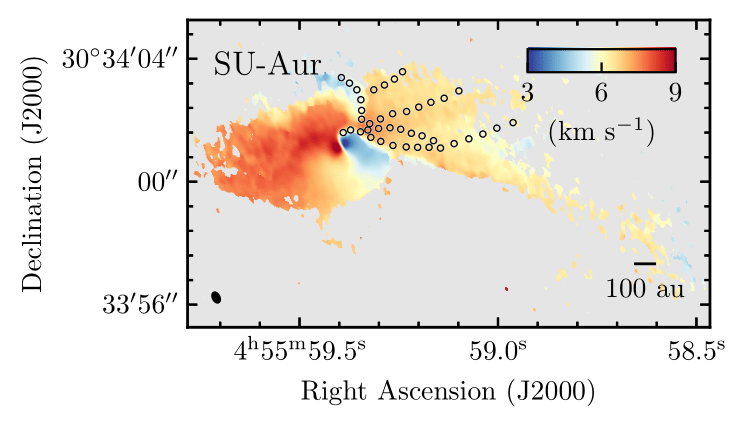
Ginski et al. 2021
Yen et al. 2019
Garufi et al. 2021
Pineda et al. 2020
50 au
BHB1 (Alves et al. 2020), GM Aur (Huang et al. 2021), IRS 63 (Segura-Cox in prep.), AB Aur (Grady et al. 1999 / Fukagawa et al. 2004), M512 Grant et al. 2021, Gupta et al. 2024, Cacciapuoti et al. 2024), ...
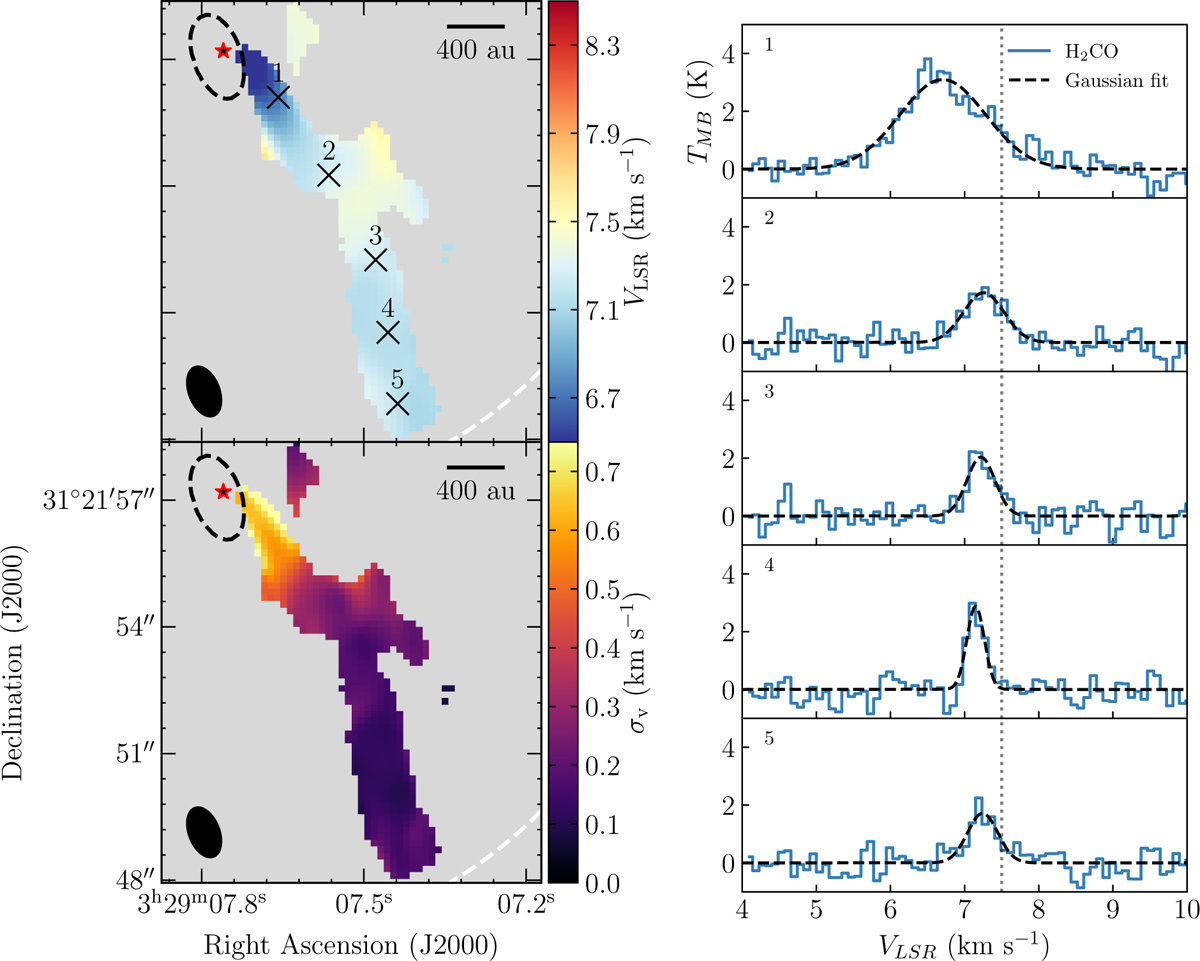
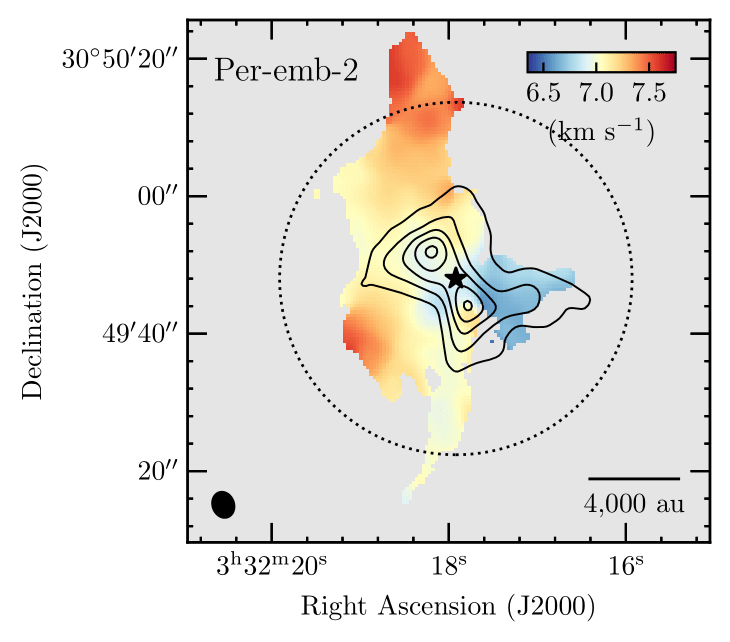
Per-emb-50
Valdivia-Mena et al. 2022
Science question:
Can we get better (statistical) constraints on the relevance and importance of (late) infall from existing simulation data?
Streamers:
Model star formation in a Molecular Cloud
isothermal magnetohydrodynamical (MHD) with driven turbulence
adaptive mesh refinement (AMR) simulations with RAMSES
maximum resolution: ≈25 au (level of refinement: 15), root grid about ≈1600 au (level 9)
Total mass: 3000 solar masses
periodic boundary conditions
altogether 321 sink particles at last snapshot (2 Myr after the formation of the first star)
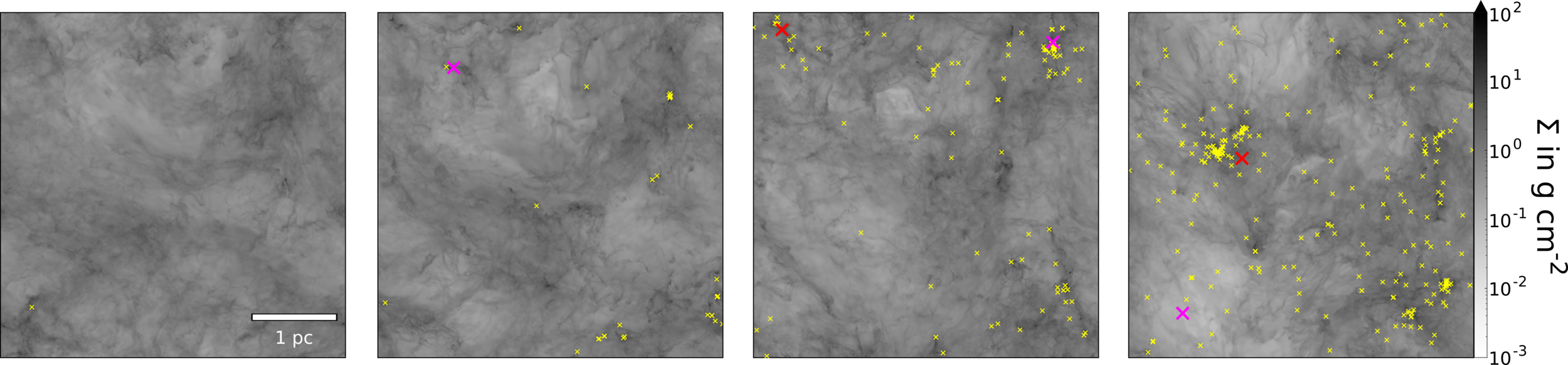
simulation setup including detailed description of sink recipe presented in Haugbølle+2018
Küffmeier, Jensen & Haugbølle '23
Late infall is common for stars*
*unless they remain tiny
On average, stars with final masses of more than 1 solar mass accrete more than 50 % of their mass after 500 kyr
Note that some protostars still accrete after 1.2 Myr
Küffmeier, Jensen & Haugbølle '23
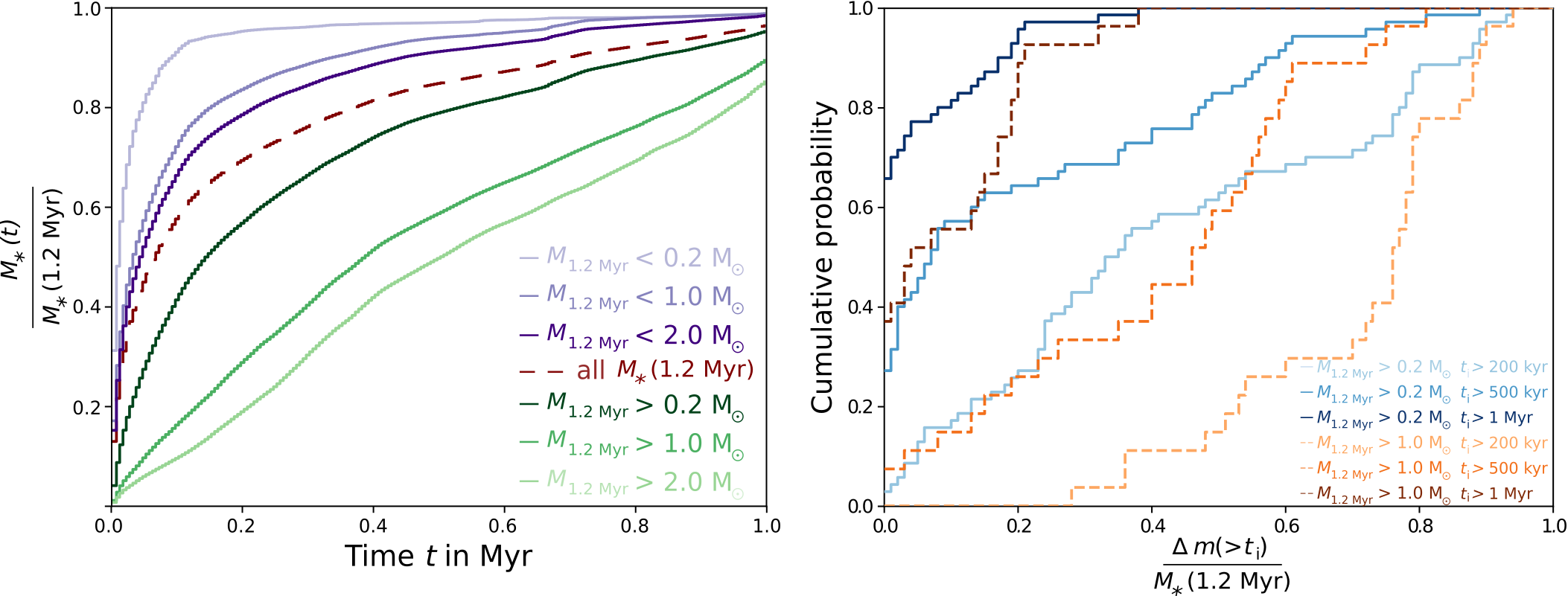
Origin of accreting gas
Two phase process:
Initial collapse followed by varying amount of post-collapse infall
(see also Smith+ 2011, Kuznetsova et al. 2020, Pelkonen+ 2021)
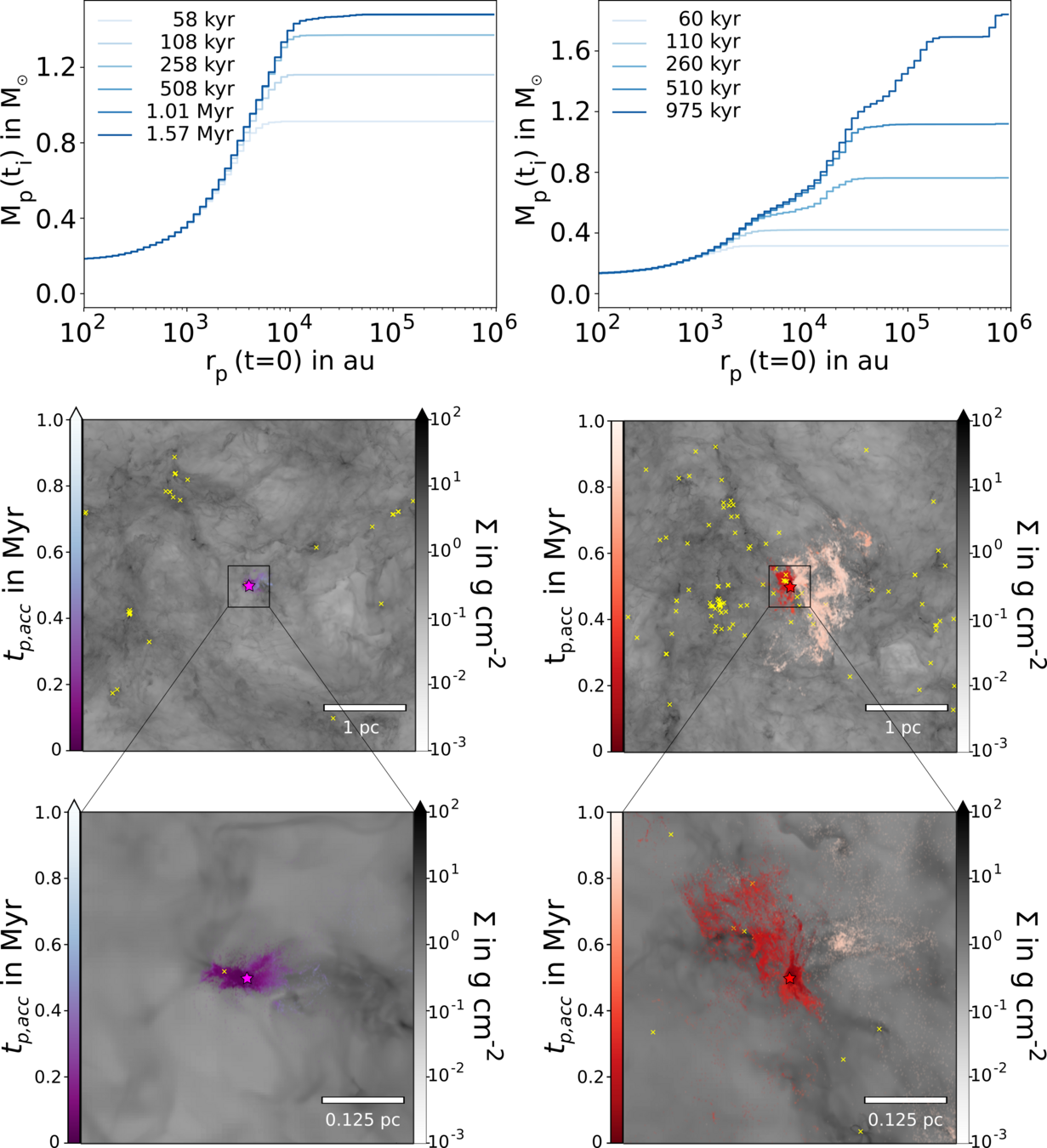
Küffmeier, Jensen & Haugbølle '23
YSOs can appear younger than they really are
How old is the protostar?
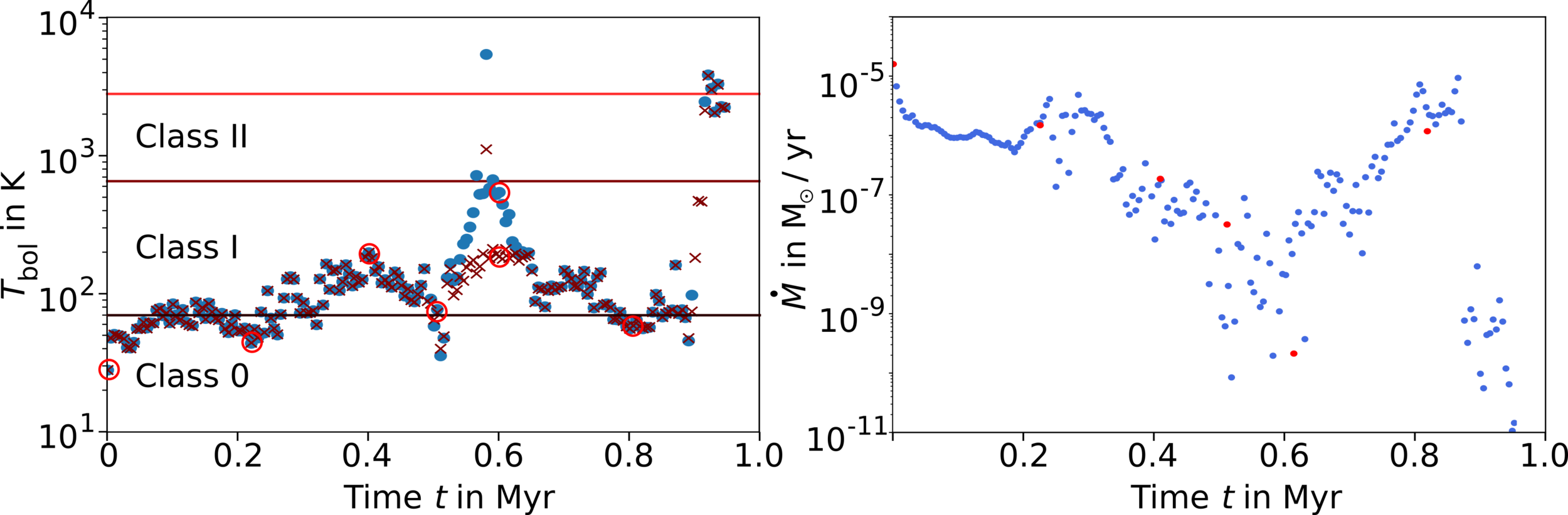
Küffmeier, Jensen & Haugbølle '23
Angular momentum budget
- Large scatter of ang. mom.
- Increasing specific angular momentum for increasing final stellar mass
Specific angular momentum computed from all accreting tracer particles at the first snapshot after star formation
- subtle correlation with mass (inherited by disks??)
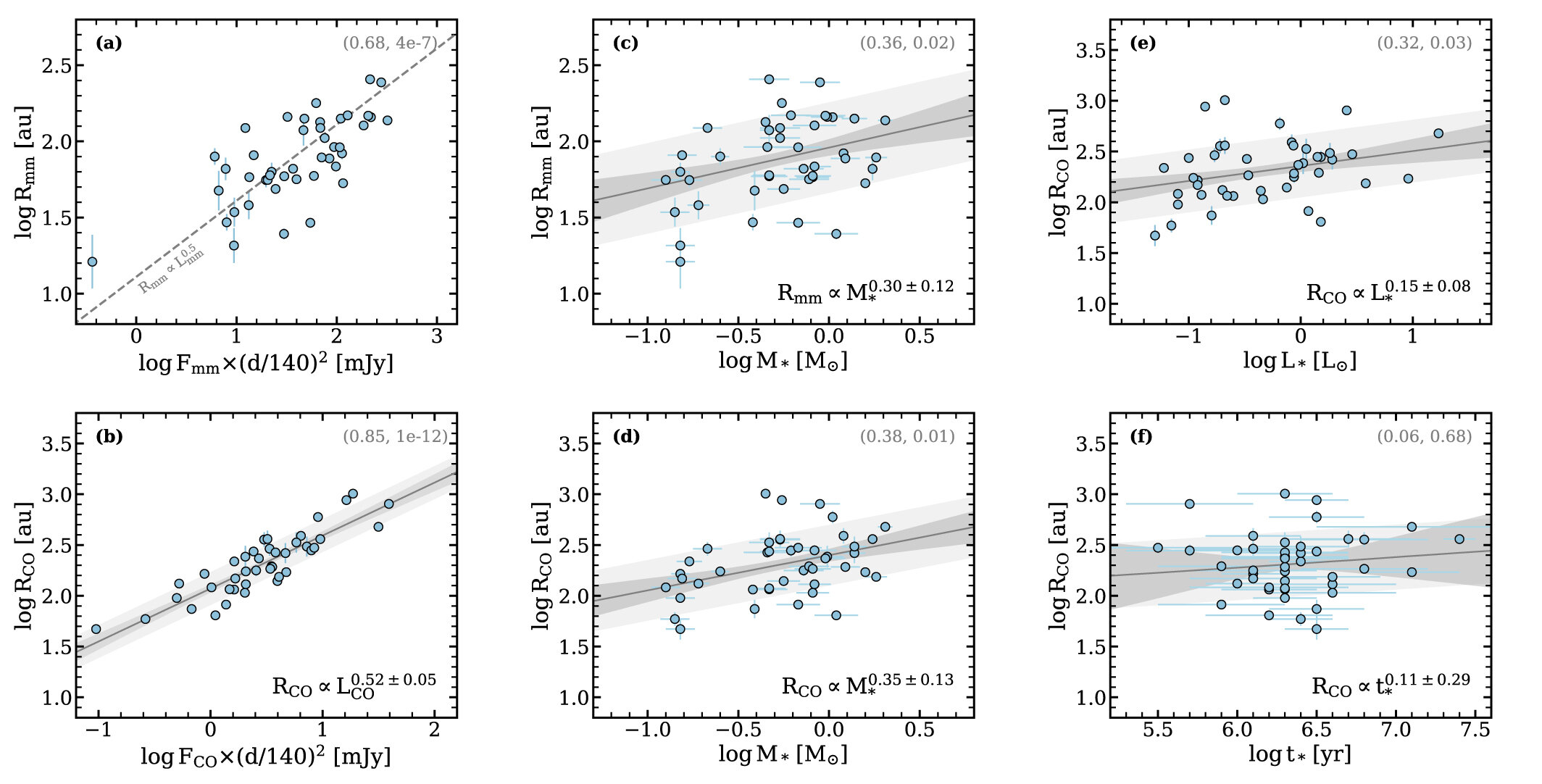
"We find marginal relationships between disk sizes and M*." (Long+ 2022)
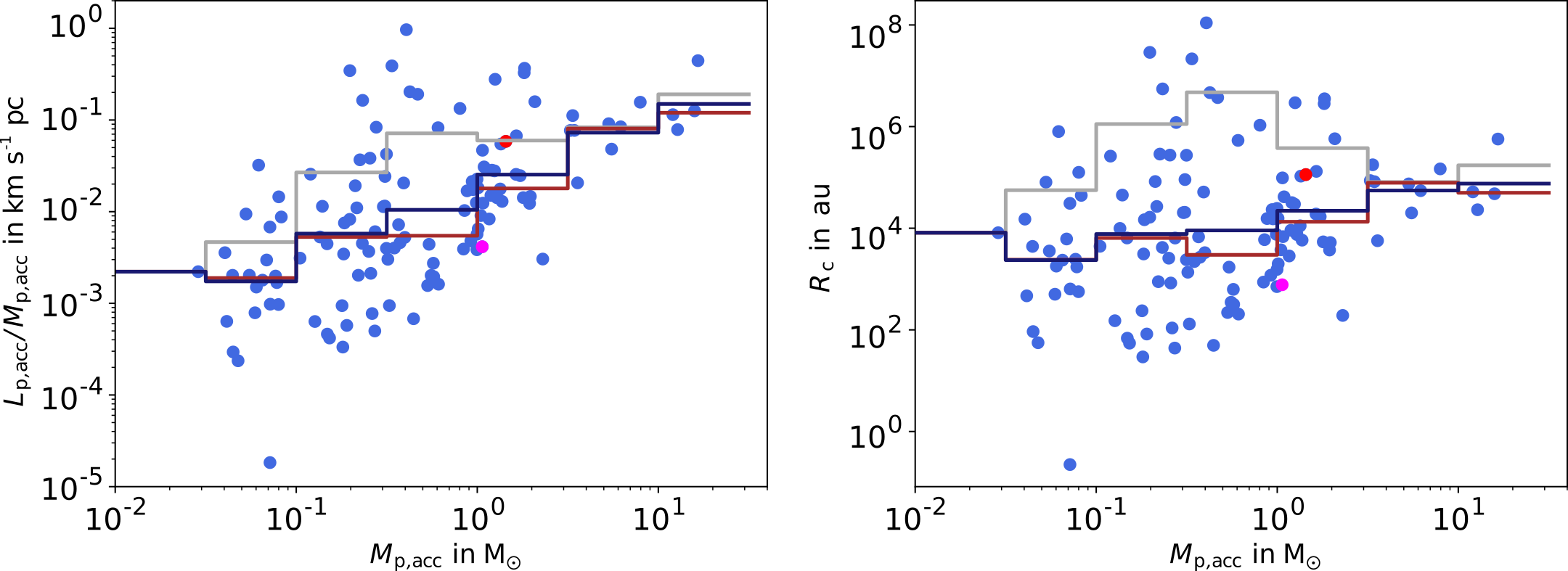
Küffmeier, Jensen & Haugbølle '23
On average, stars with increasing final mass undergo prolonged infall
Orientation of star-disk systems can change substantially
Küffmeier, Haugbølle, Pineda & Segura-Cox in prep
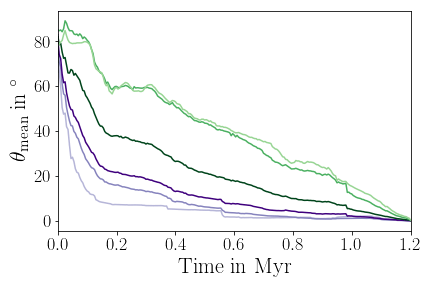
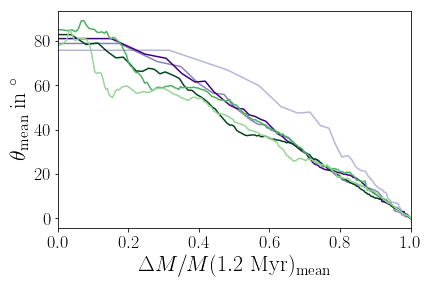
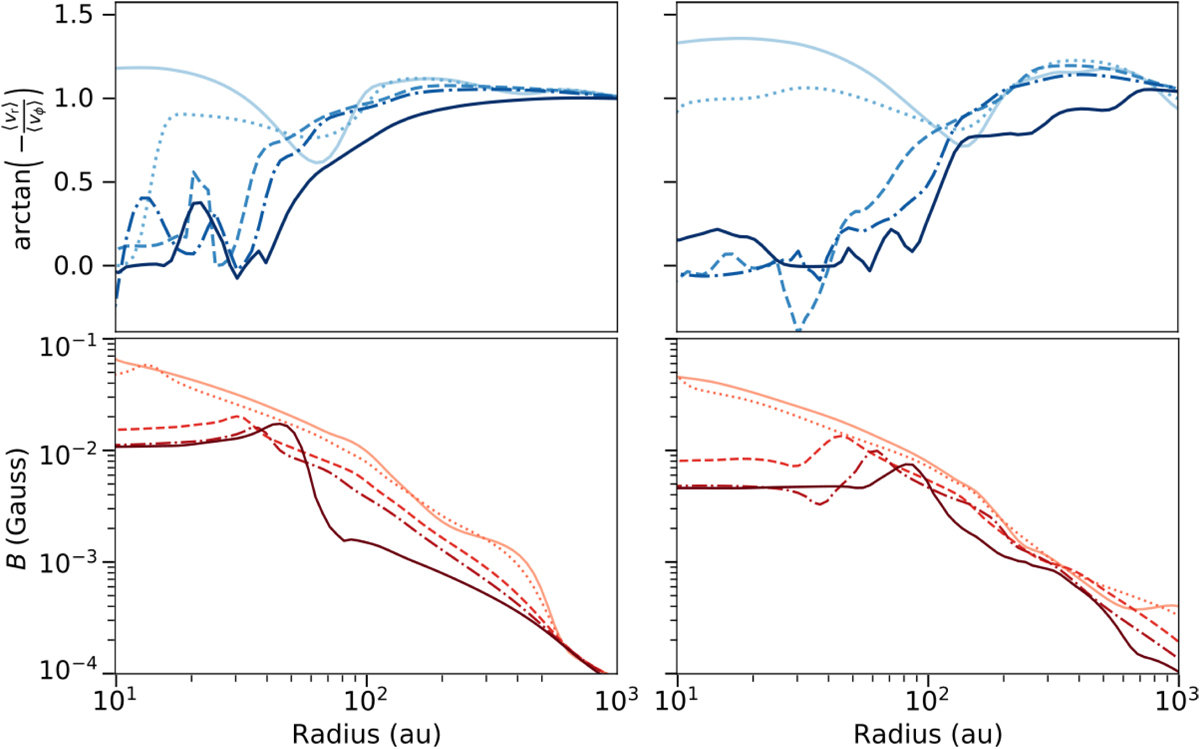
Post-collapse infall is more anisotropic than initial collapse
Orientation of infall
Streamers & shadows: signs of infall
Formation of misaligned configuration
synthetic image
Krieger, Kuffmeier et al. 2024
Kuffmeier, Dullemond, Reissl & Goicovic 2021
Ginski et al. 2021 (see also Labdon et al. 2023)
300 au
in agreement with Bate 2018 (see also next talk by Deng)
Credit: NASA/ESA Hubble space telescope &
ALMA (ESO/NAOJ/NRAO)
The big challenge:
link planet to star formation
50 au
Zoom-in on embedded stars
Kuffmeier et al.
2019
Kuffmeier et al. 2018
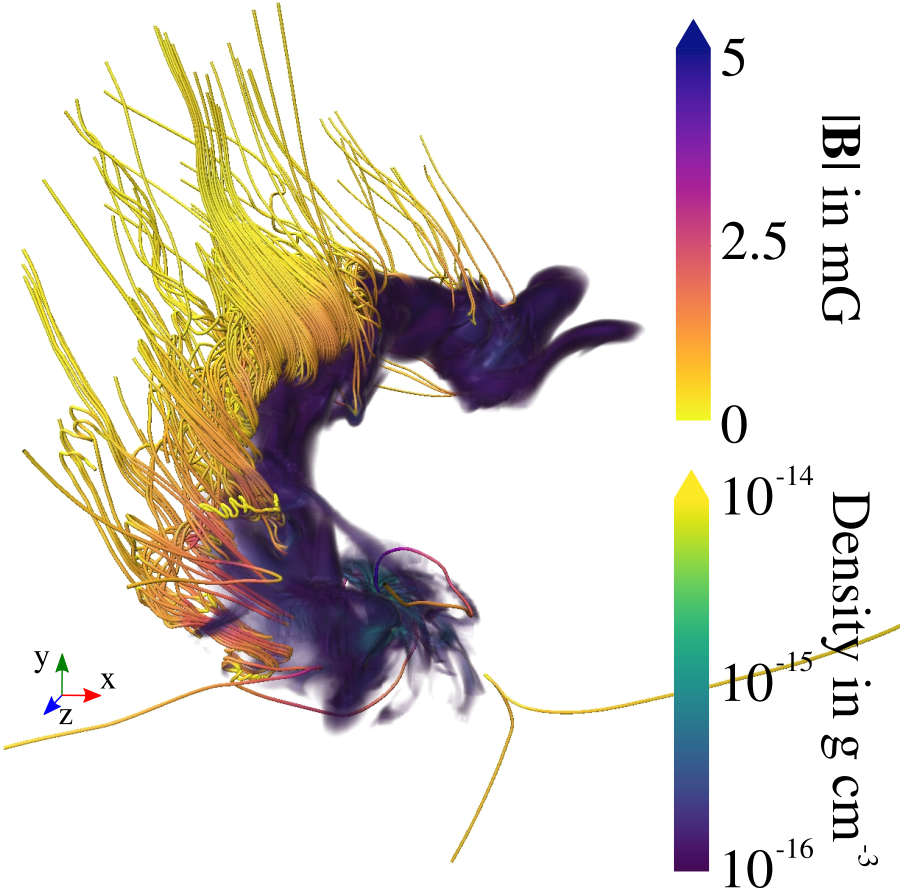
Kuffmeier, Reißl et al. 2020
bridge structure similar to IRAS 16293--2422 (e.g. Sadavoy+ 2018, van der Wiel+ 2019, Maureira+ 2020)
~1500 AU
Pro: self-consistent initial and boundary conditions for star formation
Con: computationally more expensive, more difficult analysis
for zoom-in from clump to disk with non-ideal MHD, see also Lebreuilly et al. 2024
To do: link advanced multi-physics state-of-the-art collapse models to multi-scale models
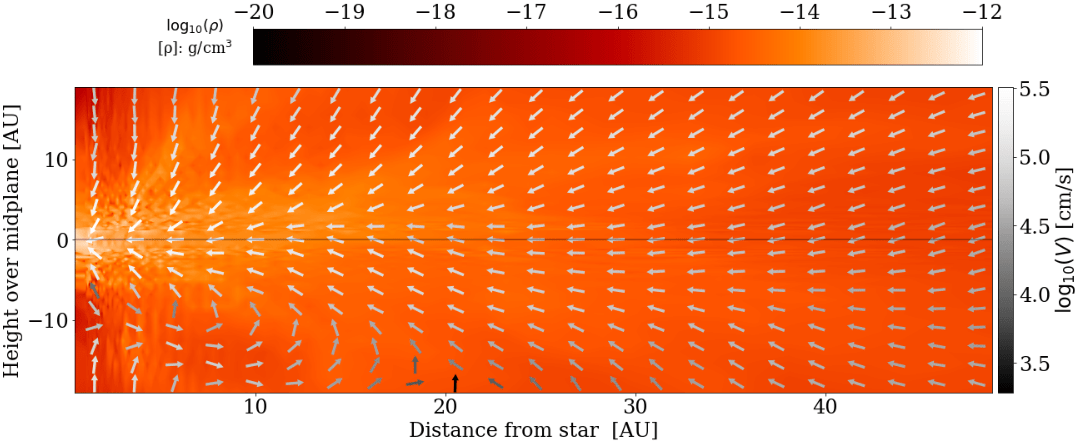
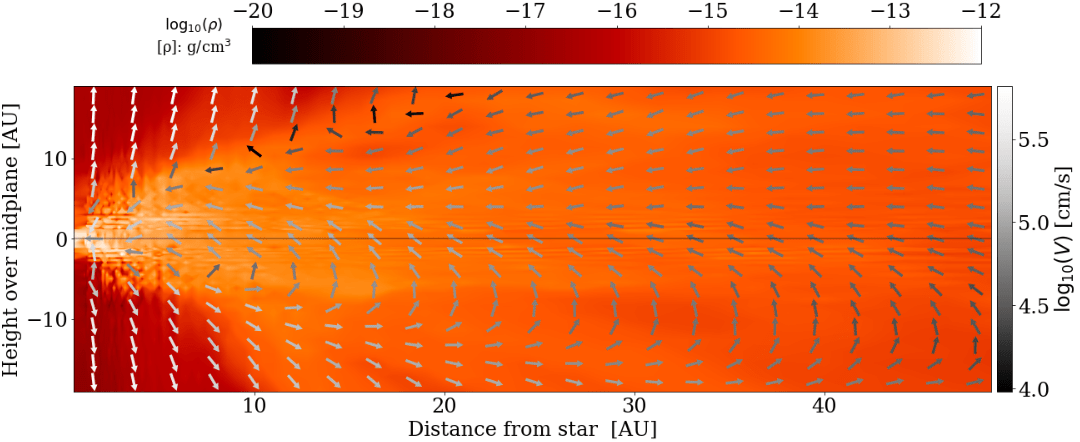
How do infall and outflow affect the disk?
Christian G. Holm
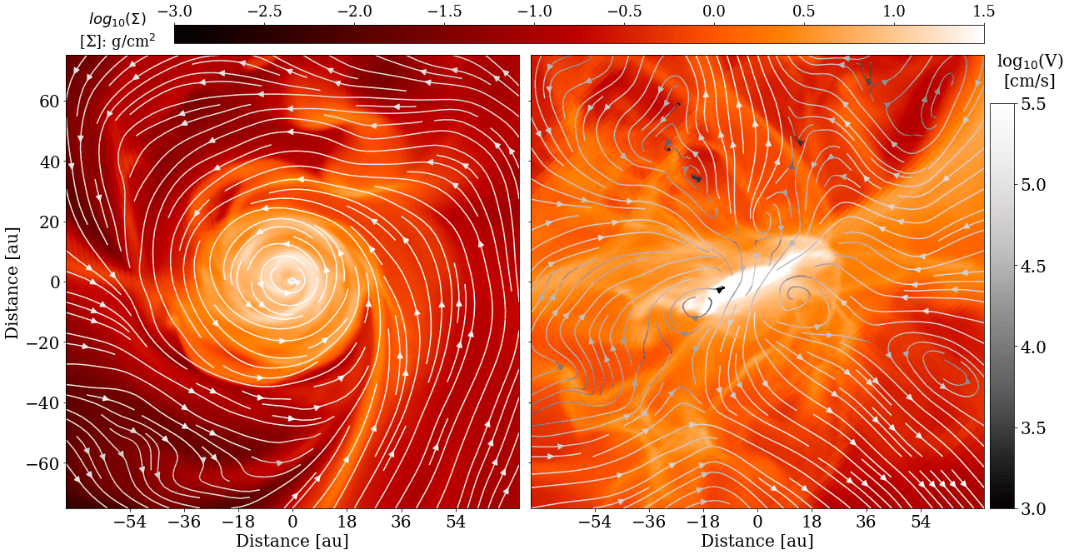
Zoom-in simulation*, 0.1 au resolution in disk, barotropic equation of state
*(run with DISPATCH: used only 1 instead of 24 nodes, yet ~10 times faster than RAMSES)
Christian G. Holm
How do infall and outflow affect the disk?
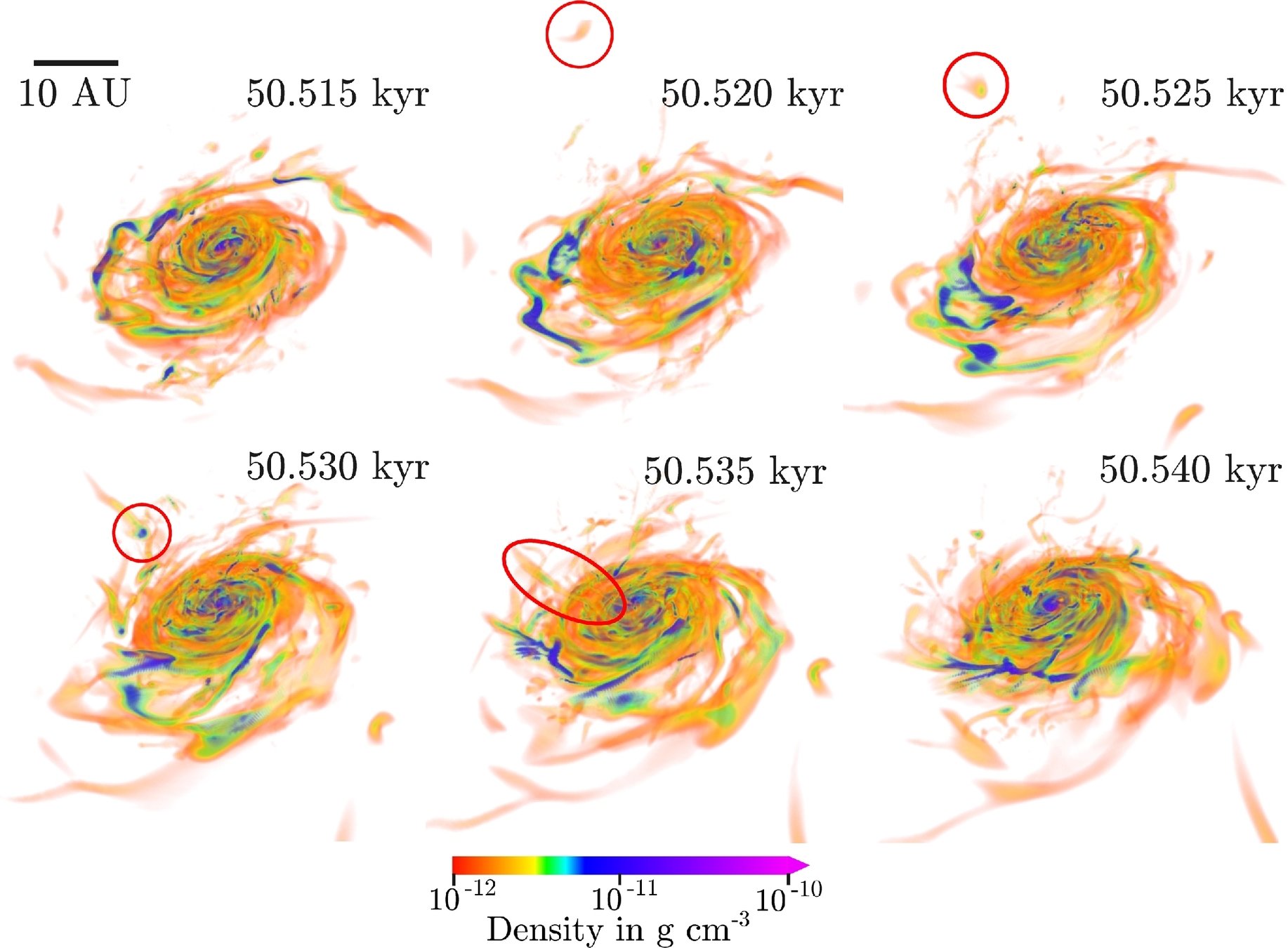
star A, t = 13 kyr
star A, t = 25 kyr
strong magnetic braking,
strong outflow
How do infall and outflow affect the disk?
Christian G. Holm
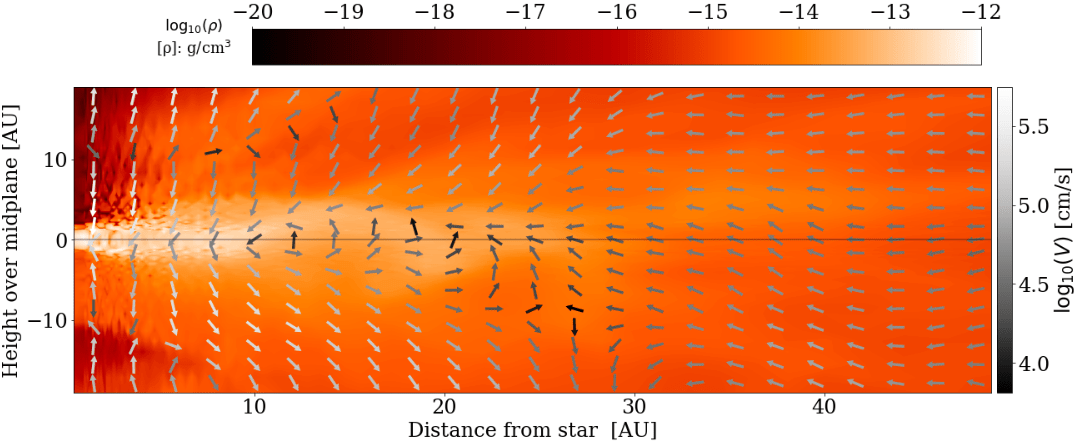
simultaneous infall and magnetically-driven outflow
star B, t = 30 kyr
- Is the disk solely replenished with fresh material?
- Does infall frequently lead to the formation of a new misaligned outer disk (and if yes, for how long)?
- Is (late) infall catastrophic? Does it form a completely new disk?
Key questions to be addressed in multi-scale models
- Which percentage of ejected material returns?
(see Tsukamoto et al. 2021 ["ash-fall"], Cacciapuoti et al. 2024 ["protostellar chimney flues"])
- What about perturbations by companion/flyby?
(talks by Smallwood and Martin)
Summary
Stars & disks are replenished and distorted by misaligned infall
YSOs can be rejuvenated
Star formation is a two-phase process:
initial collapse + post-collapse infall phase
Magnetic fields ...
- induce magnetic braking, which depends on ionization-rate
- launch outflows
Kuffmeier subm.
Christian G. Holm
How do infall and outflow affect the disk?
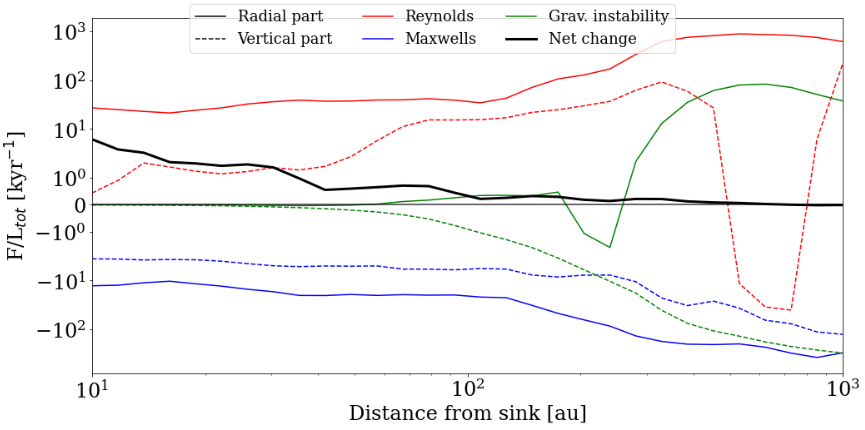
Angular momentum transport via magnetic braking
What fraction of the gas and dust returns to the disk after being ejected by an outflow?
Key question
Credit: Tsukamoto et al. 2021
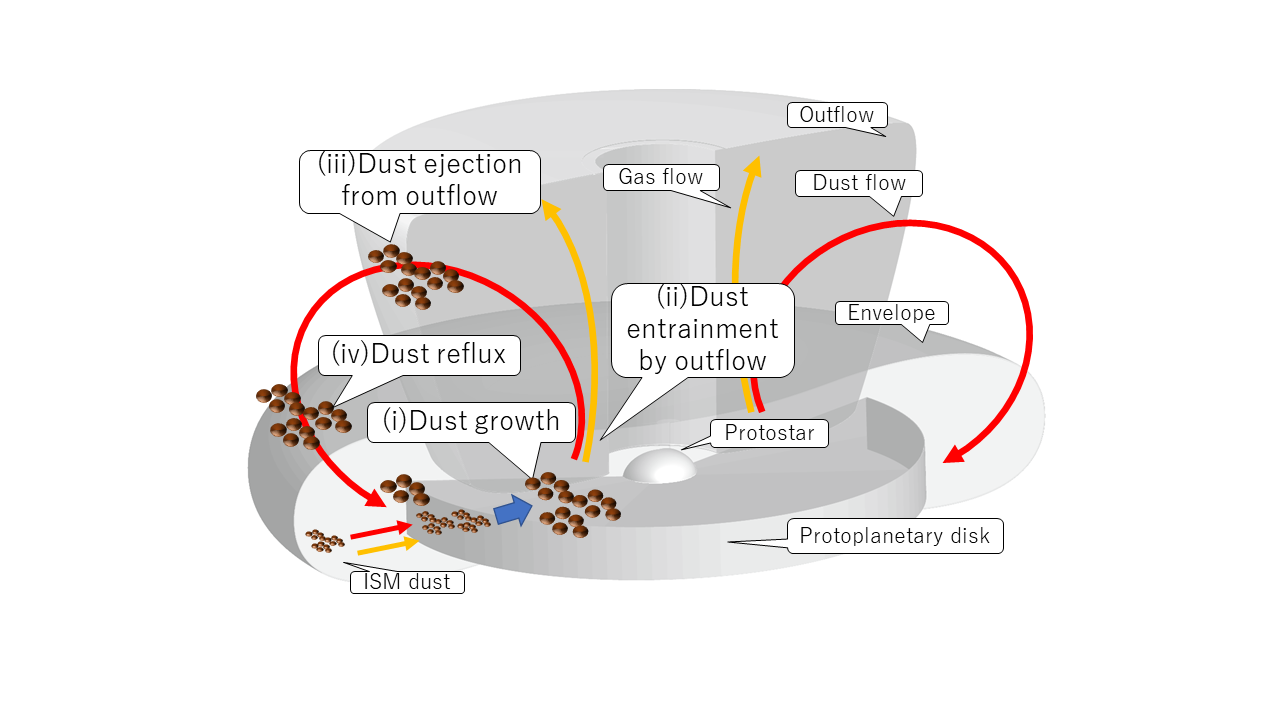
"Ash-fall" scenario aka conveyor belt
Increase in dust-to-gas ratio because dust can grow in disk and return
Tsukamoto et al. 2021
magnetohydrodynamics
\frac{\partial \mathbf{B}}{\partial t} = \nabla\times (\mathbf{v}\times\mathbf{B})
ideal MHD
\color{red}-\nabla\times[\eta_{\rm O} (\nabla \times \mathbf{B})]
\color{purple}-\nabla\times \{\eta_{\rm H} [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}
\color{blue}-\nabla\times \{\eta_{\rm AD} \mathbf{B}/B \times [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}
Ohmic dissipation
Hall
ambipolar diffusion
Non-ideal
Non-ideal MHD
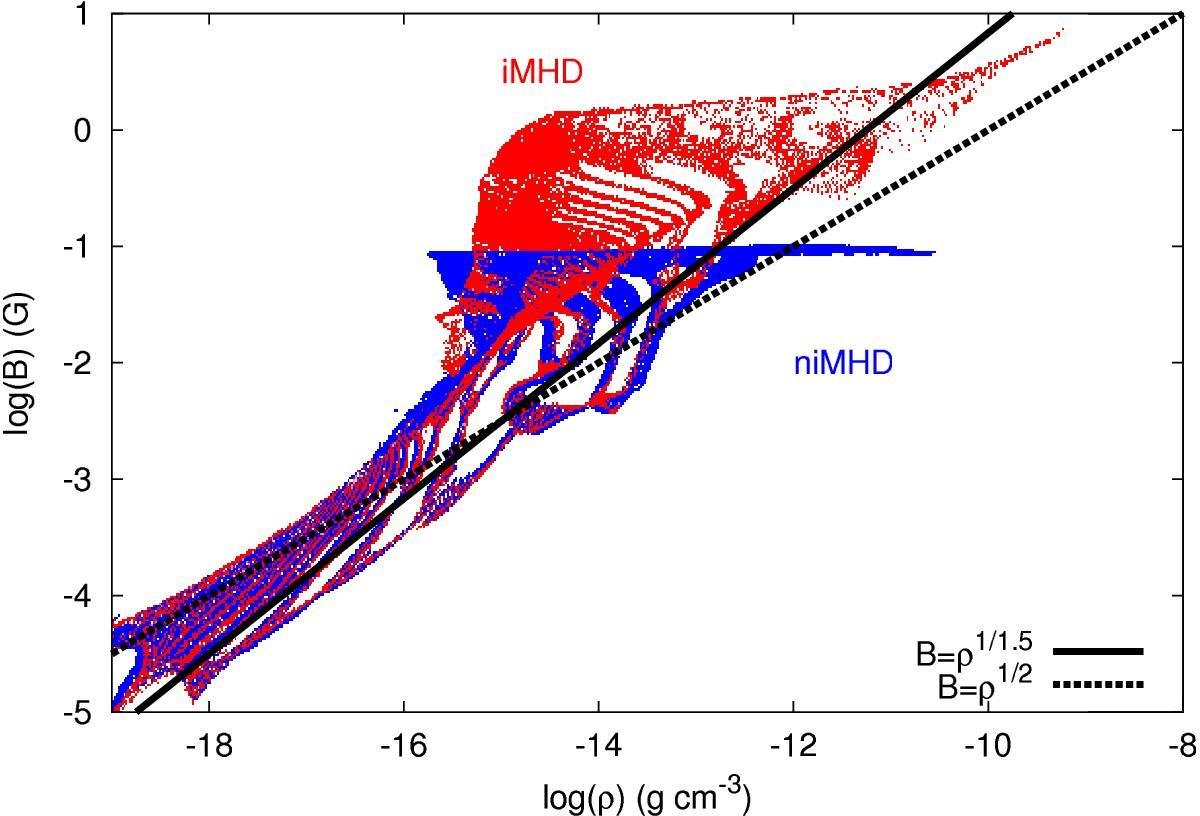
Masson et al. 2016
resistivities quench pile-up of magnetic field
avoids magnetic braking catastrophe
see Hennebelle et al. 2016 or Lee et al. 2021 for analytical studies
more references in reviews by Wurster & Li 2018 and Tsukamoto et al. 2023
Effect of ionization on disk size
increasing ionization rate
enhanced magnetic braking
smaller disks
Küffmeier, Zhao & Caselli 2020
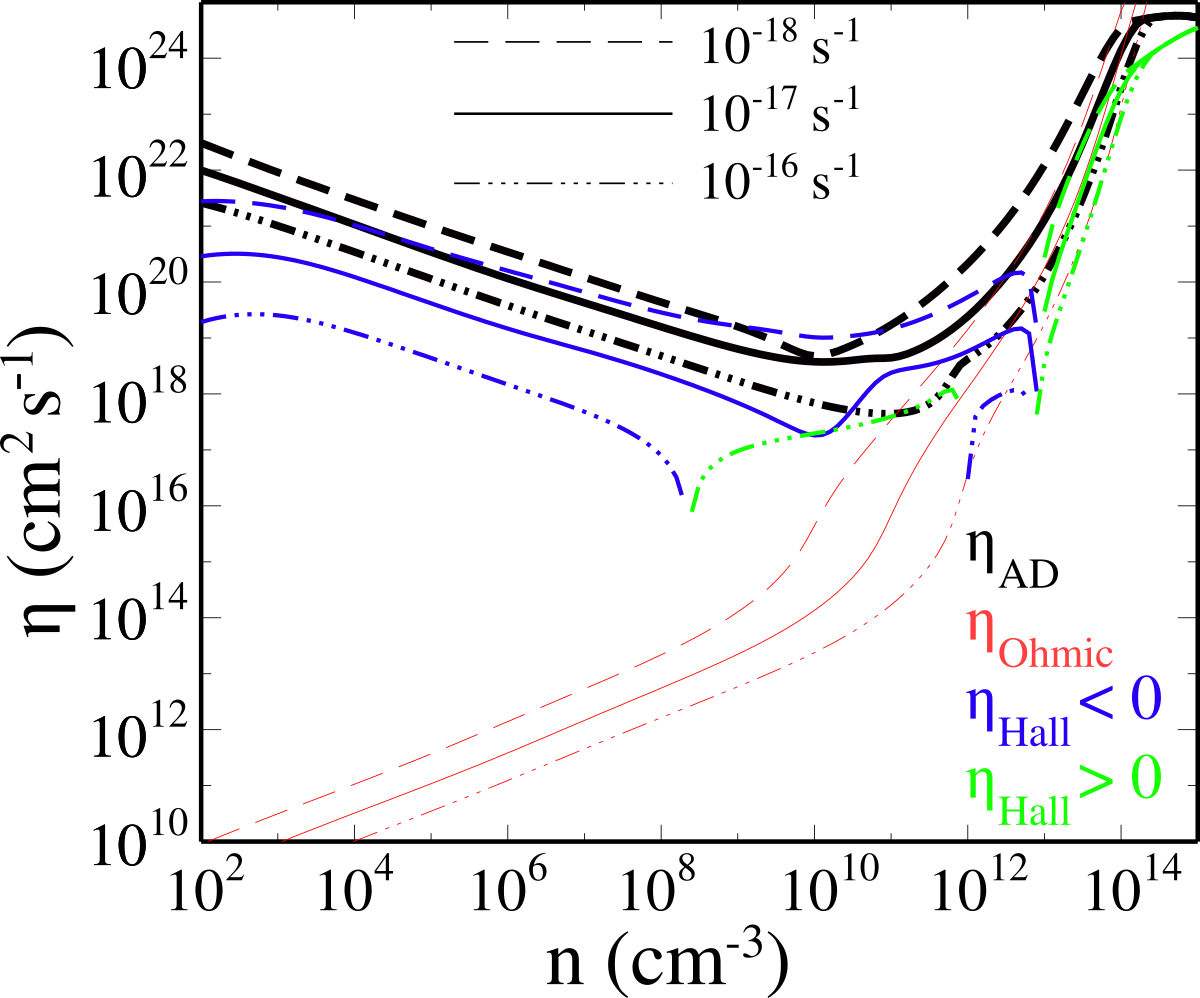
rotation
infall
from light to dark colors: high to low ionization rates
see also Wurster et al. 2018
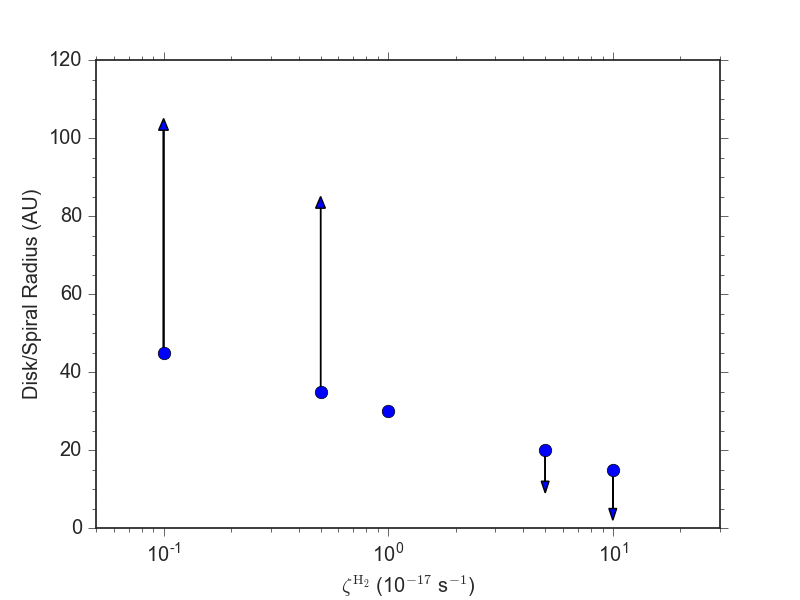
Effect of ionization on disk size
increasing ionization rate
enhanced magnetic braking
smaller disks
see also Wurster et al. 2018
Küffmeier, Zhao & Caselli 2020
Origin of accreting gas
"In the case of the more massive stars, accretion from the environment outside the original core volume is even more important than that from the core itself. [...]
The assumption of spherical symmetry cannot be applied to the majority of collapsing cores, and is never a good description of how stars accrete gas from outside the original core radius."
(Smith et al. 2011)
\mathrm{FA} = \sqrt{ \frac{1}{2}} \frac{\sqrt{(\lambda_1 - \lambda_2)^2 + (\lambda_2 - \lambda_3)^2 + (\lambda_3 - \lambda_1)^2}}{\sqrt{\lambda_1^2 + \lambda_2^2 + \lambda_3^2}}
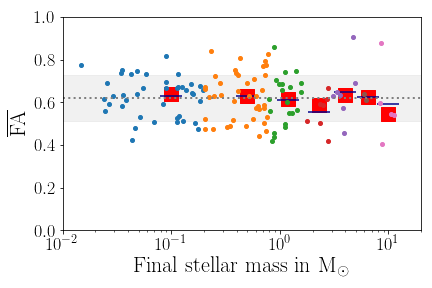
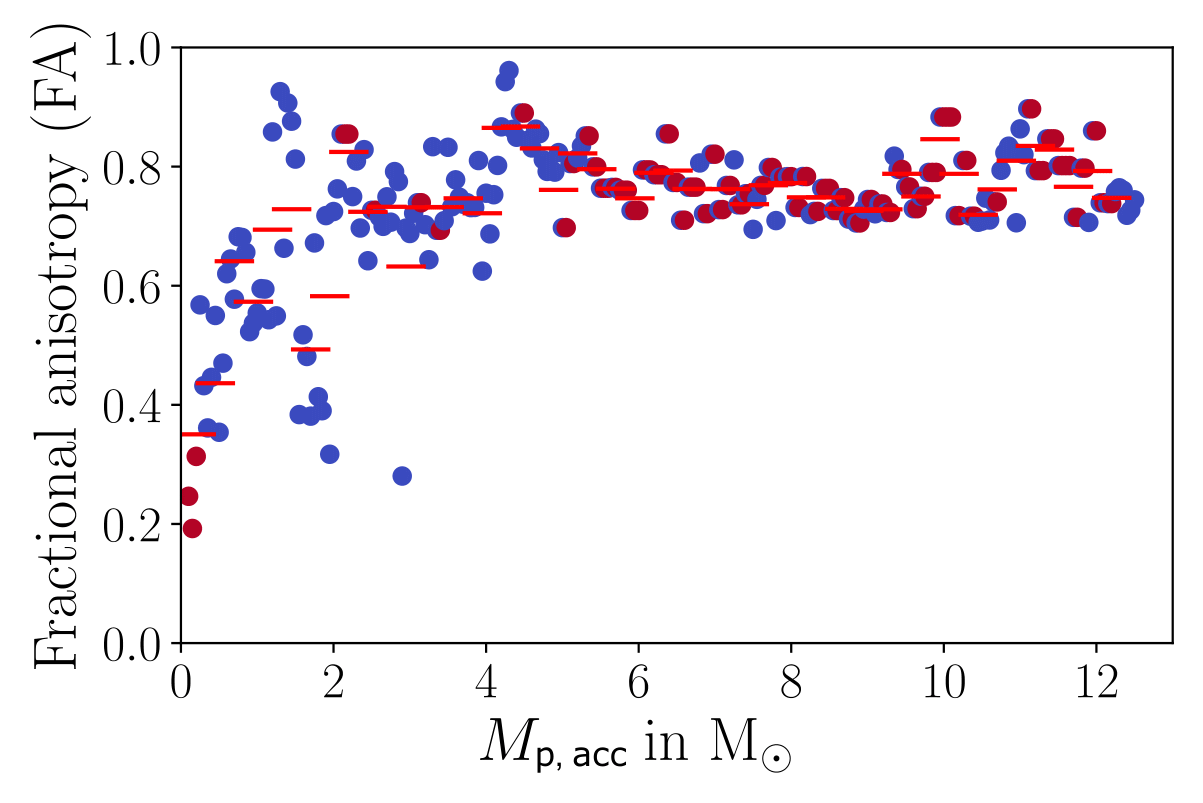
Fractional anisotropy based on tracer particles
Fractional anisotropy (FA) serves as a good measure for the (an-)isotropy of accretion.
FA=0: perfectly isotropic accretion, FA=1: maximally anisotropic
FA can also be a useful measure to compare (an)isotropy of stellar spins in clusters
Late infall is more anisotropic than early collapse
\mathrm{FA} = \sqrt{ \frac{1}{2}} \frac{\sqrt{(\lambda_1 - \lambda_2)^2 + (\lambda_2 - \lambda_3)^2 + (\lambda_3 - \lambda_1)^2}}{\sqrt{\lambda_1^2 + \lambda_2^2 + \lambda_3^2}}
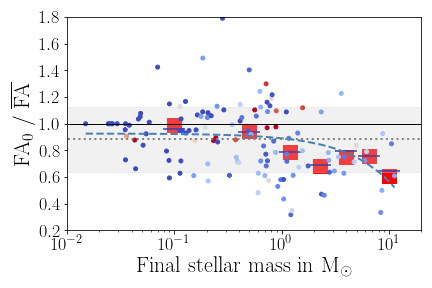
Fractional anisotropy (FA) serves as a good measure for the (an-)isotropy of accretion.
FA=0: perfectly isotropic accretion, FA=1: maximally anisotropic
\frac{\Delta t_{\rm single}}{\Delta t_{\rm single}+\Delta t_{\rm mult}}
1
0
FA can also be a useful measure to compare (an)isotropy of stellar spins in clusters
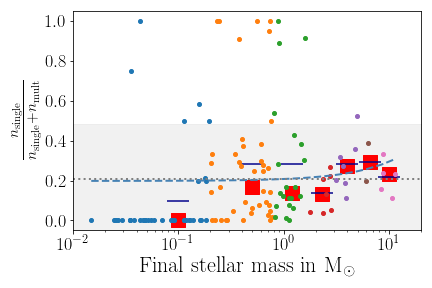
Accretion as single star or as part of multiple
Possible trend that lower mass stars are more likely to be part of binary or systems of higher order during accretion
Sendai workshop: Modeling embedded disks with infall through streamers
By kuffmeier
