Quantum Dynamic Capacity & Superadditivity 

  • arXiv:0811.4227 with M. Wilde
  • arXiv:0901.3038 with M. Wilde
  • arXiv:1708.04314 with Y. Zhu, Q. Zhung, and P. Shor
\langle\mathcal{N} \rangle \geq R[c\to c]+ Q[q\to q]+ E[qq]
⟨N⟩≥R[c→c]+Q[q→q]+E[qq]\langle\mathcal{N} \rangle \geq R[c\to c]+ Q[q\to q]+ E[qq]

Quantum Dynamic Protocols

[MH & M.Wilde, arXiv:0901.3038]
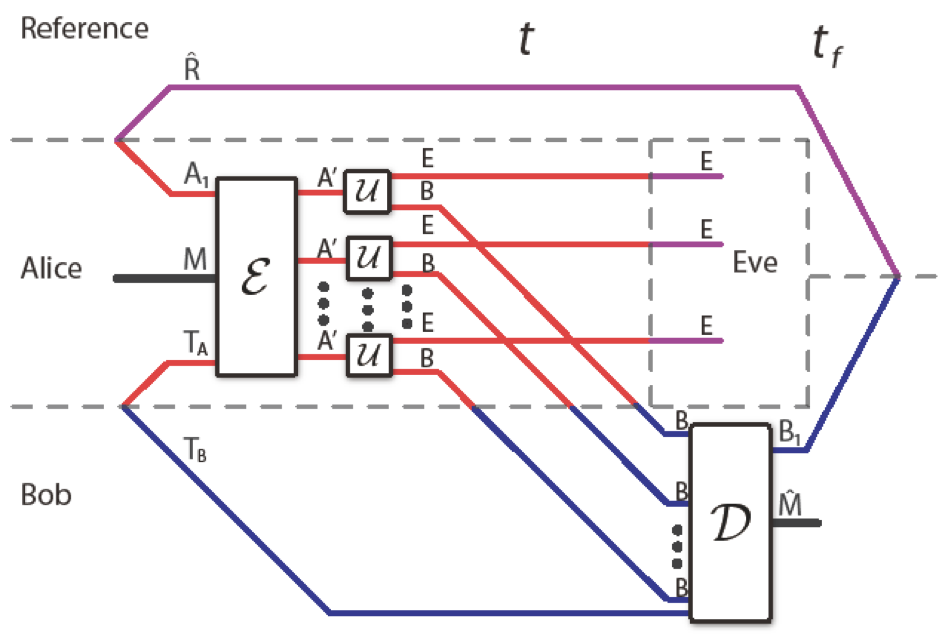
C(\mathcal{N})= \left\{(R,Q,E): \right.
C(N)={(R,Q,E):C(\mathcal{N})= \left\{(R,Q,E): \right.

Quantum Dynamic Capacity

a quantum dynamic protocol exists.}

\langle\mathcal{N}\rangle + |E|[qq] \geq R[c\to c]+ Q[q\to q]
⟨N⟩+∣E∣[qq]≥R[c→c]+Q[q→q]\langle\mathcal{N}\rangle + |E|[qq] \geq R[c\to c]+ Q[q\to q]

EA-assisted C-Q Communication

R= I(X:B)_\sigma
R=I(X:B)σR= I(X:B)_\sigma
Q= \frac{1}{2}I(A:B|X)_\sigma
Q=12I(A:B∣X)σQ= \frac{1}{2}I(A:B|X)_\sigma
|E|= \frac{1}{2}I(A:E|X)_\sigma
∣E∣=12I(A:E∣X)σ|E|= \frac{1}{2}I(A:E|X)_\sigma
[MH & M.Wilde, arXiv:0811.4227]

Special Cases

\langle\mathcal{N} \rangle \geq R[c\to c]
⟨N⟩≥R[c→c]\langle\mathcal{N} \rangle \geq R[c\to c]
\langle\mathcal{N} \rangle \geq Q[q\to q]
⟨N⟩≥Q[q→q]\langle\mathcal{N} \rangle \geq Q[q\to q]
\langle\mathcal{N} \rangle \geq R[c\to c] + Q[q\to q]
⟨N⟩≥R[c→c]+Q[q→q]\langle\mathcal{N} \rangle \geq R[c\to c] + Q[q\to q]
\langle\mathcal{N}\rangle +|E|[qq] \geq R[c\to c]
⟨N⟩+∣E∣[qq]≥R[c→c]\langle\mathcal{N}\rangle +|E|[qq] \geq R[c\to c]
\langle\mathcal{N} \rangle+|E|[qq] \geq Q[q\to q]
⟨N⟩+∣E∣[qq]≥Q[q→q]\langle\mathcal{N} \rangle+|E|[qq] \geq Q[q\to q] 
SD
TP
ED

EACQ Capacity Region

R+2Q\leq I(AX:B)_\sigma
R+2Q≤I(AX:B)σR+2Q\leq I(AX:B)_\sigma
Q\leq I(A\rangle BX)_\sigma +|E|
Q≤I(A⟩BX)σ+∣E∣ Q\leq I(A\rangle BX)_\sigma +|E|
R+Q\leq I(X:B)_\sigma + I(A\rangle BX)_\sigma +|E|
R+Q≤I(X:B)σ+I(A⟩BX)σ+∣E∣R+Q\leq I(X:B)_\sigma + I(A\rangle BX)_\sigma +|E|
\{
{\{
C^{(1)}_\sigma(\mathcal{N})
Cσ(1)(N)C^{(1)}_\sigma(\mathcal{N})
C^{(1)}(\mathcal{N})=\bigcup_\sigma C^{(1)}_\sigma(\mathcal{N})
C(1)(N)=⋃σCσ(1)(N)C^{(1)}(\mathcal{N})=\bigcup_\sigma C^{(1)}_\sigma(\mathcal{N})
C(\mathcal{N})=\overline{\bigcup_{k=1}^{\infty} \frac{1}{k}C^{(1)}_\sigma(\mathcal{N}^{\otimes k})}
C(N)=⋃k=1∞1kCσ(1)(N⊗k)‾C(\mathcal{N})=\overline{\bigcup_{k=1}^{\infty} \frac{1}{k}C^{(1)}_\sigma(\mathcal{N}^{\otimes k})}
\text{SD:} [q\to q]+[qq]\geq 2[c\to c]
SD:[q→q]+[qq]≥2[c→c]\text{SD:} [q\to q]+[qq]\geq 2[c\to c]
\text{TP:} [qq]+2[c\to c]\geq [q\to q]
TP:[qq]+2[c→c]≥[q→q]\text{TP:} [qq]+2[c\to c]\geq [q\to q]
\text{ED:} [q\to q]\geq [qq]
ED:[q→q]≥[qq]\text{ED:} [q\to q]\geq [qq]

Quantum Dynamic Capacity

R+2Q\leq I(AX:B)_\sigma
R+2Q≤I(AX:B)σR+2Q\leq I(AX:B)_\sigma
Q+E\leq I(A\rangle BX)_\sigma
Q+E≤I(A⟩BX)σ Q+E\leq I(A\rangle BX)_\sigma
R+Q+E\leq I(X:B)_\sigma + I(A\rangle BX)_\sigma
R+Q+E≤I(X:B)σ+I(A⟩BX)σR+Q+E\leq I(X:B)_\sigma + I(A\rangle BX)_\sigma
\{
{\{
C^{(1)}_\sigma(\mathcal{N})
Cσ(1)(N)C^{(1)}_\sigma(\mathcal{N})
C^{(1)}(\mathcal{N})=\bigcup_\sigma C^{(1)}_\sigma(\mathcal{N})
C(1)(N)=⋃σCσ(1)(N)C^{(1)}(\mathcal{N})=\bigcup_\sigma C^{(1)}_\sigma(\mathcal{N})
C(\mathcal{N})=\overline{\bigcup_{k=1}^{\infty} \frac{1}{k}C^{(1)}_\sigma(\mathcal{N}^{\otimes k})}
C(N)=⋃k=1∞1kCσ(1)(N⊗k)‾C(\mathcal{N})=\overline{\bigcup_{k=1}^{\infty} \frac{1}{k}C^{(1)}_\sigma(\mathcal{N}^{\otimes k})}

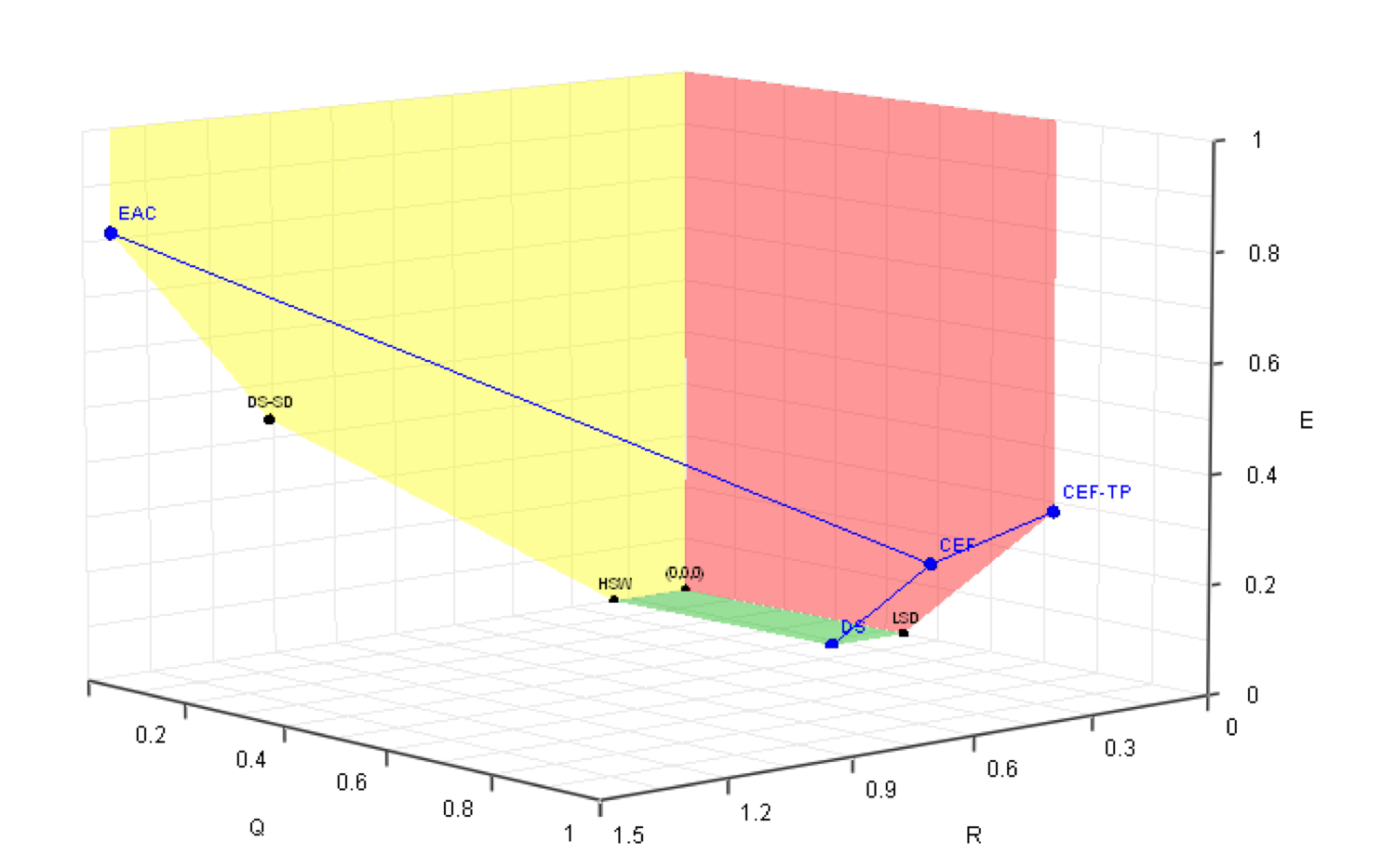
Dynamic Achievable Region

Quantum Dephasing Channels

Additivity

C(\mathcal{N})=\overline{\bigcup_{k=1}^{\infty} \frac{1}{k}C^{(1)}_\sigma(\mathcal{N}^{\otimes k})}
C(N)=⋃k=1∞1kCσ(1)(N⊗k)‾C(\mathcal{N})=\overline{\bigcup_{k=1}^{\infty} \frac{1}{k}C^{(1)}_\sigma(\mathcal{N}^{\otimes k})}
\stackrel{?}{=}
=?\stackrel{?}{=}
C^{(1)}_\sigma(\mathcal{N})
Cσ(1)(N)C^{(1)}_\sigma(\mathcal{N})

Additivity

Type Additive?
Classical Capacity
Quantum Capacity
EA-assisted Classical Capacity
EA-assisted C-Q Capacity

N

N

N

Y

Additive CE CQ QE
C
Ｑ
Ｃ＆Ｑ

Additivity?

Implies the trade-off additivity?

N

N

N

Y

Y

N

N

N

N

Implies the trade-off additivity?
​Additive CQE
QE
CQ
CE
CE&Q
CE&CQ

Additivity?

Y

N

N

N

N

[MH & M.Wilde, arXiv:0901.3038]

Proof Ingredients

A Switch Channel such that

C^{(1)}_{CQE}(\mathcal{N}) = \text{conv}\left( C^{(1)}_{CQE}(\mathcal{N_0}),C^{(1)}_{CQE}(\mathcal{N_1}) \right)
CCQE(1)(N)=conv(CCQE(1)(N0),CCQE(1)(N1))C^{(1)}_{CQE}(\mathcal{N}) = \text{conv}\left( C^{(1)}_{CQE}(\mathcal{N_0}),C^{(1)}_{CQE}(\mathcal{N_1}) \right)

Proof Ingredients

\text{If}\quad C_{CQE}(\mathcal{N}_0) = C^{(1)}_{CQE}(\mathcal{N}_0)
IfCCQE(N0)=CCQE(1)(N0)\text{If}\quad C_{CQE}(\mathcal{N}_0) = C^{(1)}_{CQE}(\mathcal{N}_0)
\text{then}
then\text{then}
C_{CQE}(\mathcal{N}) = \text{conv}\left( C_{CQE}(\mathcal{N_0}),C_{CQE}(\mathcal{N_1}) \right)
CCQE(N)=conv(CCQE(N0),CCQE(N1))C_{CQE}(\mathcal{N}) = \text{conv}\left( C_{CQE}(\mathcal{N_0}),C_{CQE}(\mathcal{N_1}) \right)

Q additive, CQ superadditive

\text{(1):}\quad C_{Q}(\mathcal{N}_0) \geq C_{Q}(\mathcal{N}_1)
(1):CQ(N0)≥CQ(N1)\text{(1):}\quad C_{Q}(\mathcal{N}_0) \geq C_{Q}(\mathcal{N}_1)
\text{(3):}\quad C_{C}(\mathcal{N}_1) > C^{(1)}_{C}(\mathcal{N}_1)
(3):CC(N1)>CC(1)(N1)\text{(3):}\quad C_{C}(\mathcal{N}_1) > C^{(1)}_{C}(\mathcal{N}_1)
\text{(2):}\quad C_{C}(\mathcal{N}_0) < C_{C}(\mathcal{N}_1)
(2):CC(N0)<CC(N1)\text{(2):}\quad C_{C}(\mathcal{N}_0) < C_{C}(\mathcal{N}_1)

Thank you for your attention!

Superadditivity in trade-off capacities of quantum channels

By Lawrence Min-Hsiu Hsieh

Made with Slides.com

Superadditivity in trade-off capacities of quantum channels

arXiv:0811.4227+arXiv:0901.3038+arXiv:1708.04314

  • 537

More from Lawrence Min-Hsiu Hsieh