General Resource Theory

Min-Hsiu Hsieh

UTS Centre for Quantum Software and Information

[1] Anurag Anshu, MH, Rahul Jain. Quantifying resource in catalytic resource theory. Accepted in Physical Review Letters. [arXiv:1708.00381].

[2] Eric Chitambar, MH. Relating the Resource Theories of Entanglement and Quantum Coherence. Physical Review Letters, vol. 117, p. 020402 (2016).

[4] Yu Luo, Yongming Li, MH. Inequivalent Multipartite Coherence Classes and New Coherence Monotones. [arXiv:1807.06308].

[3] Madhav Krishnan Vijayan, Eric Chitambar, MH. One-shot assisted concentration of coherence. [arXiv:1804.06554]

Resource Theory

(1): Free States

(2): Free Operations

Part I:

How to quantity the amount of resources?

[1] Anurag Anshu, MH, Rahul Jain. Quantifying resource in catalytic resource theory. Accepted in Physical Review Letters. [arXiv:1708.00381].

Main Result:

The amount of resource in \(\rho_M\) is equal to \(E^\infty(\rho_M)\)

E(\rho_M)= \inf_{\sigma_M\in\mathcal{F}} D(\rho_M\|\sigma_M)
E(ρM)=infσM∈FD(ρM∥σM)E(\rho_M)= \inf_{\sigma_M\in\mathcal{F}} D(\rho_M\|\sigma_M)

It works for 

1. Free States form a convex and close set.

2. Free States remain free under tensor product and partial trace.

Concrete Examples

1. Entanglement

2. Coherence

3. Asymmetry

4. Purity

Regularized Relative Entropy of Entanglement is a right measure for the "quantumness".

Resolved an open question in [1].

[1] Groisman, Popescu, and Winter, “Quantum, classical, and total amount of correlations in a quantum state,” Phys. Rev. A, vol. 72, p. 032317,  2005.

Remark

Setup

1. The amount of resource equals the amount of noise used to erase it. 

2. Catalyst is allowed. 

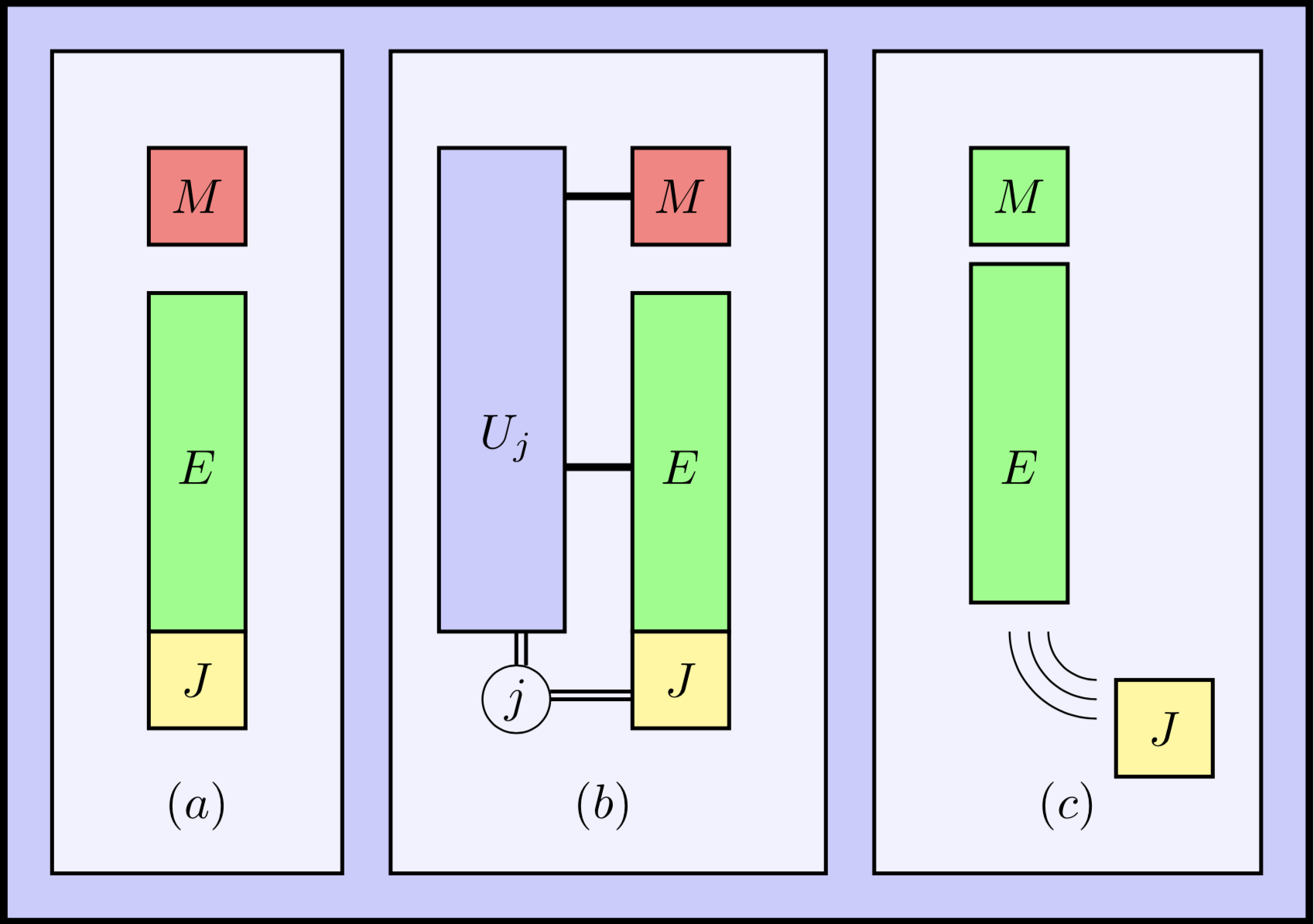
Remark

1. Matching one-shot bounds. 

2. Convex Splitting Lemma is used. 

Part II:

Interplay of Entanglement and Coherence Resources

[2] Eric Chitambar, MH. Relating the Resource Theories of Entanglement and Quantum Coherence. PRL, vol. 117, p. 020402 (2016).

|\Phi_A\rangle:=\sqrt{1/2}(|0\rangle^A+|1\rangle^A)
∣ΦA⟩:=1/2(∣0⟩A+∣1⟩A)|\Phi_A\rangle:=\sqrt{1/2}(|0\rangle^A+|1\rangle^A)
|\Phi_{A'B'}\rangle:=\sqrt{1/2}(|00\rangle+|11\rangle)
∣ΦA′B′⟩:=1/2(∣00⟩+∣11⟩)|\Phi_{A'B'}\rangle:=\sqrt{1/2}(|00\rangle+|11\rangle)
\mathcal{L}\left(\Phi_A^{\otimes\lceil n(R_A+\epsilon)\rceil}\otimes\Phi_B^{\otimes\lceil n(R_B+\epsilon)\rceil}\otimes\Phi_{A'B'}^{\otimes\lceil n(E^{co}+\epsilon)\rceil}\right)
L(ΦA⊗⌈n(RA+ϵ)⌉⊗ΦB⊗⌈n(RB+ϵ)⌉⊗ΦA′B′⊗⌈n(Eco+ϵ)⌉)\mathcal{L}\left(\Phi_A^{\otimes\lceil n(R_A+\epsilon)\rceil}\otimes\Phi_B^{\otimes\lceil n(R_B+\epsilon)\rceil}\otimes\Phi_{A'B'}^{\otimes\lceil n(E^{co}+\epsilon)\rceil}\right)
{\approx}_{\epsilon}\ \ \rho^{\otimes n}
≈ϵ  ρ⊗n{\approx}_{\epsilon}\ \ \rho^{\otimes n}

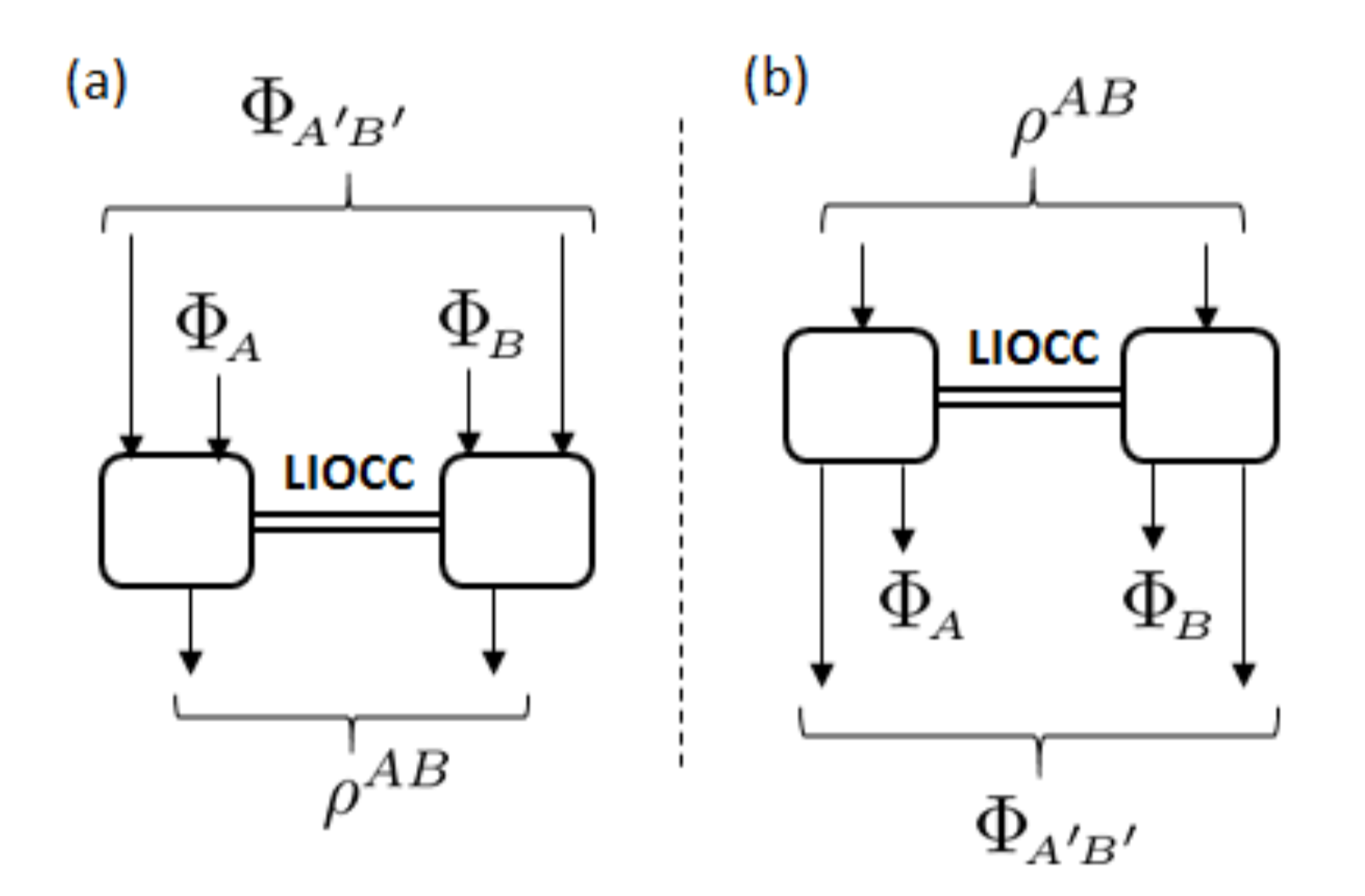
(a) Coherence - Entanglement Formation 

What is known...

\mathcal{L}\left(\Phi_A^{\otimes\lceil n(R_A+\epsilon)\rceil}\right)
L(ΦA⊗⌈n(RA+ϵ)⌉)\mathcal{L}\left(\Phi_A^{\otimes\lceil n(R_A+\epsilon)\rceil}\right)
{\approx}_{\epsilon}\ \ \rho^{\otimes n}
≈ϵ  ρ⊗n{\approx}_{\epsilon}\ \ \rho^{\otimes n}

\(R_A\geq S(X)_{\Delta(\Psi_A)}\), 

[*]  X. Yuan, H. Zhou, Z. Cao, and X. Ma, Phys. Rev. A 92, 022124 (2015). 

[*]  A. Winter and D. Yang, Phys. Rev. Lett. 116, 120404 (2016).
\geq C_F(\rho)
≥CF(ρ)\geq C_F(\rho)

(i) \(E^{co}\geq \mathrm{E}(\Psi)\), 

(ii) \(R_A+R_B\geq S(XY)_{\Delta(\Psi)}\),

(iii) \(R_B+E^{co}\geq S(XY)_{\Delta(\Psi)}\)

Result (a)

For a pure state \(|\Psi_{AB}\rangle\),

Remark

We result coincide with formation of a mixed state \(\rho\) is given by \(C_F(\rho)\) [1].

[1] A. Winter and D. Yang, Phys. Rev. Lett. 116, 120404 (2016).

However, we need extra \(E^{co}\geq \mathrm{E}(\Psi)\) because of the distributed settings.

Let \(C_M(\Psi):=S(X)_{\Delta(\Psi)}+S(Y)_{\Delta(\Psi)}-{E}(\Psi).\)

\(C_M(\Psi)\) is an LIOCC monotone. 

\(C_M(\Psi)=C_a^{A|B}(\Psi)+C_r(\Psi^A).\)

Proof:

Theorem:

\(C_M(\Psi):=S(X)_{\Delta(\Psi)}+S(Y)_{\Delta(\Psi)}-{E}(\Psi).\)

Remark

is an LIOCC monotone, but  not an LOCC monotone

(b) Coherence - Entanglement Distillation 

\Phi_A^{\otimes\lceil n(R_A-\epsilon)\rceil}\otimes\Phi_B^{\otimes\lceil n(R_B-\epsilon)\rceil}\otimes\Phi_{A'B'}^{\otimes\lceil n(E^{co}-\epsilon)\rceil}
ΦA⊗⌈n(RA−ϵ)⌉⊗ΦB⊗⌈n(RB−ϵ)⌉⊗ΦA′B′⊗⌈n(Eco−ϵ)⌉\Phi_A^{\otimes\lceil n(R_A-\epsilon)\rceil}\otimes\Phi_B^{\otimes\lceil n(R_B-\epsilon)\rceil}\otimes\Phi_{A'B'}^{\otimes\lceil n(E^{co}-\epsilon)\rceil}
\mathcal{L} (\rho^{\otimes n}) {\approx}_{\epsilon}
L(ρ⊗n)≈ϵ\mathcal{L} (\rho^{\otimes n}) {\approx}_{\epsilon}

What is known...

\mathcal{L} (\rho^{\otimes n}) {\approx}_{\epsilon}
L(ρ⊗n)≈ϵ\mathcal{L} (\rho^{\otimes n}) {\approx}_{\epsilon}
\Phi_A^{\otimes\lceil n(R_A-\epsilon)\rceil}
ΦA⊗⌈n(RA−ϵ)⌉\Phi_A^{\otimes\lceil n(R_A-\epsilon)\rceil}

\(R_A\leq S(X)_{\Delta(\Psi_A)}\), 

[*]  A. Winter and D. Yang, Phys. Rev. Lett. 116, 120404 (2016).

Result (b)

For a pure state \(|\Psi_{AB}\rangle\),

(i) \(R_A+R_B\leq C_{M}(\Psi)\) 

(ii) \(R_B+E^{co}\leq S(Y)_{\Delta(\Psi)}\)

(iii) \(E^{co} \to \) our paper.

Coherence deficit

\delta(\rho^{AB})=C_D^{Global}(\rho^{AB})-C_D^{LIOCC}(\rho^{AB})
δ(ρAB)=CDGlobal(ρAB)−CDLIOCC(ρAB)\delta(\rho^{AB})=C_D^{Global}(\rho^{AB})-C_D^{LIOCC}(\rho^{AB})
\delta_c(\rho^{AB})=C_D^{LIOCC}(\rho^{AB})-C_D^{LIO}(\rho^{AB})
δc(ρAB)=CDLIOCC(ρAB)−CDLIO(ρAB)\delta_c(\rho^{AB})=C_D^{LIOCC}(\rho^{AB})-C_D^{LIO}(\rho^{AB})
=\mathrm{E}(\Psi)-I(X:Y)_{\Delta(\Psi)}
=E(Ψ)−I(X:Y)Δ(Ψ)=\mathrm{E}(\Psi)-I(X:Y)_{\Delta(\Psi)}
=\mathrm{E}(\Psi)
=E(Ψ)=\mathrm{E}(\Psi)

Part III:

Assisted distillation of resources

[3] Madhav Krishnan Vijayan, Eric Chitambar, MH. One-shot assisted concentration of coherence. [arXiv:1804.06554]
E_{c}(\psi , \epsilon) := \max_{m \in \mathbb{N}} \left\lbrace m : \right.
Ec(ψ,ϵ):=maxm∈N{m:E_{c}(\psi , \epsilon) := \max_{m \in \mathbb{N}} \left\lbrace m : \right.
\left. \max_{\Lambda \in \mathcal{O}} F^2(\Lambda(\psi), \Phi_{2}^{\otimes m}) \geq 1- \epsilon \right\rbrace
maxΛ∈OF2(Λ(ψ),Φ2⊗m)≥1−ϵ}\left. \max_{\Lambda \in \mathcal{O}} F^2(\Lambda(\psi), \Phi_{2}^{\otimes m}) \geq 1- \epsilon \right\rbrace

One-Shot Assisted distillation of resource

E_{c}(\psi, \epsilon) \leq \max\limits_{\overline{\psi} \in b_*^{\prime}(\psi, 2\epsilon)} G_{min}(\overline{\psi})
Ec(ψ,ϵ)≤maxψ‾∈b∗′(ψ,2ϵ)Gmin(ψ‾)E_{c}(\psi, \epsilon) \leq \max\limits_{\overline{\psi} \in b_*^{\prime}(\psi, 2\epsilon)} G_{min}(\overline{\psi})
G_{\min}(\rho) = \min_{\gamma \in \mathcal{F}} [ -\log_2 \text{Tr}(\rho \gamma) ]
Gmin(ρ)=minγ∈F[−log2Tr(ργ)]G_{\min}(\rho) = \min_{\gamma \in \mathcal{F}} [ -\log_2 \text{Tr}(\rho \gamma) ]

Theorem

holds

if  \(\Phi^n \gamma \Phi^n \leq \frac{1}{2^n}\Phi^n\)

Resource

Theory

Entanglement

Coherence

Purity

G_{\min}(\psi)
Gmin(ψ)G_{\min}(\psi)
S_{\min}(\rho_\psi)
Smin(ρψ)S_{\min}(\rho_\psi)
S_{\min}(\Delta(\psi))
Smin(Δ(ψ))S_{\min}(\Delta(\psi))
\log \dim(\psi)
logdim(ψ)\log \dim(\psi)

Part IV:

Multipartite Inequivalent Coherence Classes 

[4] Yu Luo, Yongming Li, MH. Inequivalent Multipartite Coherence Classes and New Coherence Monotones. [arXiv:1807.06308].

How many are there for 3-qubit coherence states?

For 3 qubits, there are only two inequivalent entanglement classes under SLOCC.

There are already infinite many inequivalent coherence classes under SLICC for two qubits.

Main Result

# of product

terms

1
11
2
22
3
33
4
44
|00\rangle
∣00⟩|00\rangle

Classification

a|00\rangle+b|01\rangle
a∣00⟩+b∣01⟩a|00\rangle+b|01\rangle
a|00\rangle+b|10\rangle
a∣00⟩+b∣10⟩a|00\rangle+b|10\rangle
a|00\rangle+b|11\rangle
a∣00⟩+b∣11⟩a|00\rangle+b|11\rangle
a|00\rangle+b|01\rangle+c|10\rangle
a∣00⟩+b∣01⟩+c∣10⟩a|00\rangle+b|01\rangle+c|10\rangle
a|00\rangle+b|01\rangle+c|11\rangle
a∣00⟩+b∣01⟩+c∣11⟩a|00\rangle+b|01\rangle+c|11\rangle
a|00\rangle+b|01\rangle+c|10\rangle+d|11\rangle
a∣00⟩+b∣01⟩+c∣10⟩+d∣11⟩a|00\rangle+b|01\rangle+c|10\rangle+d|11\rangle
\Delta= \frac{ad}{bc}
Δ=adbc\Delta= \frac{ad}{bc}

Thank you for your attention!

General Resource Theory

By Lawrence Min-Hsiu Hsieh

Made with Slides.com

General Resource Theory

  • 622

More from Lawrence Min-Hsiu Hsieh