Common Structures in General Resource Theory

Min-Hsiu Hsieh

UTS Centre for Quantum Software and Information

Understand common structure in different Resource Theories

[Tuesday morning: Andreas Winter: Resource theories of quantum channels]

[Tuesday afternoon: Gerardo Adesso: Every convex quantum resource is useful for channel discrimination]

Outlines

  • General resource distillation

  • Hierarchy of quantum coherence operations 

  • General resource quantification

Resource Theory

(1): Free States: \(\mathcal{F}\) 

(2): Free Operations: \(\mathcal{O}\)

Part I:

How to quantity the amount of resources?

Anurag Anshu, MH, Rahul Jain. Quantifying resource in catalytic resource theory. Physical Review Letters, vol. 121, p. 190504 (2018). [arXiv:1708.00381].

Main Result:

The amount of resource in \(\rho_M\) is equal to \(E^\infty(\rho_M)\).

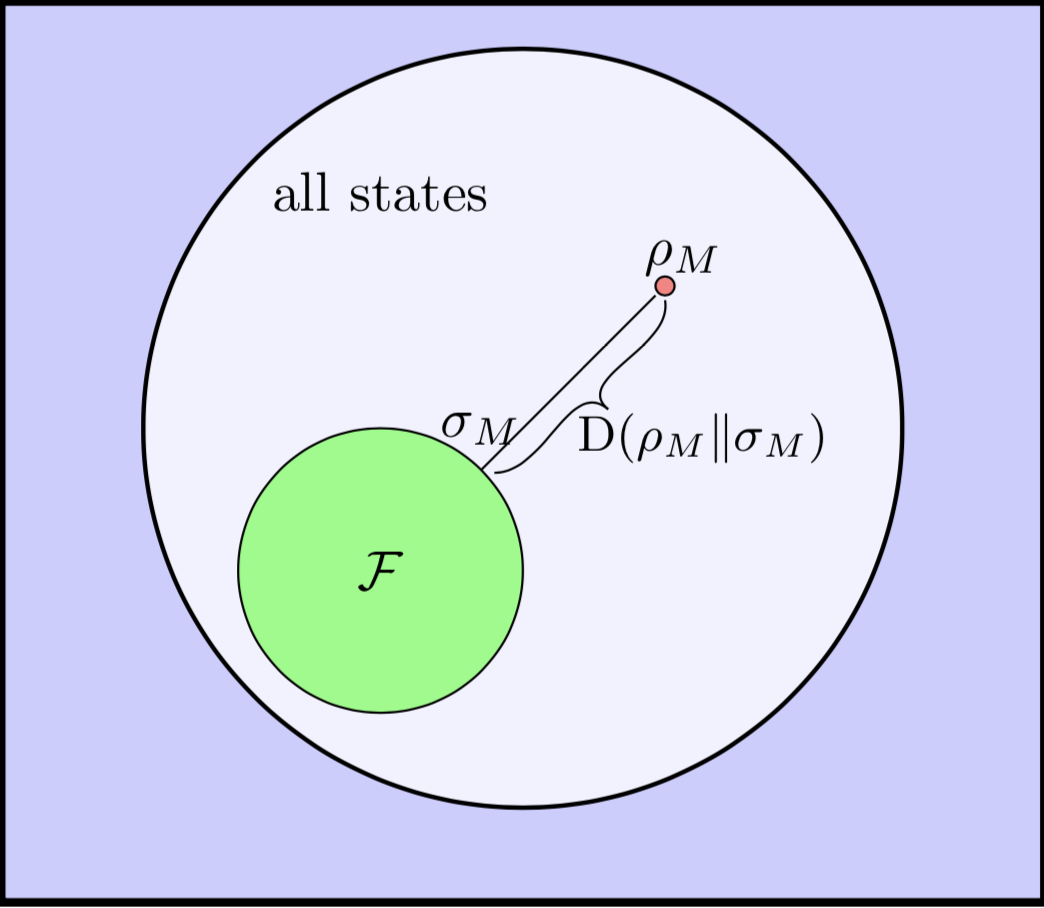
E(\rho_M)= \inf_{\sigma_M\in\mathcal{F}} D(\rho_M\|\sigma_M)

Fernando and Gilad, PRL 2015.

It works for 

1. Free States form a convex and close set.

2. Free States remain free under tensor product and partial trace.

[Tuesday morning: Andreas Winter: Resource theories of quantum channels]

Fernando and Gilad, PRL 2015.

Concrete Examples

1. Entanglement

2. Coherence

3. Asymmetry

4. Purity

Regularized Relative Entropy of Entanglement is a right measure for the "quantumness".

Resolved an open question in [1].

[1] Groisman, Popescu, and Winter, “Quantum, classical, and total amount of correlations in a quantum state,” Phys. Rev. A, vol. 72, p. 032317,  2005.

Remark

[2] Mario Berta and Christian Majenz. Phys. Rev. Lett. 121, 190503  2018.

Generalize and Recover

Setup

1. The amount of resource equals the amount of noise used to erase it. 

2. Catalyst is allowed. 

[1] Groisman, Popescu, and Winter, “Quantum, classical, and total amount of correlations in a quantum state,” Phys. Rev. A, vol. 72, p. 032317,  2005.

[Wednesday morning: Anurag Anshu: Efficient Mehod for one-shot Quantum Communication]

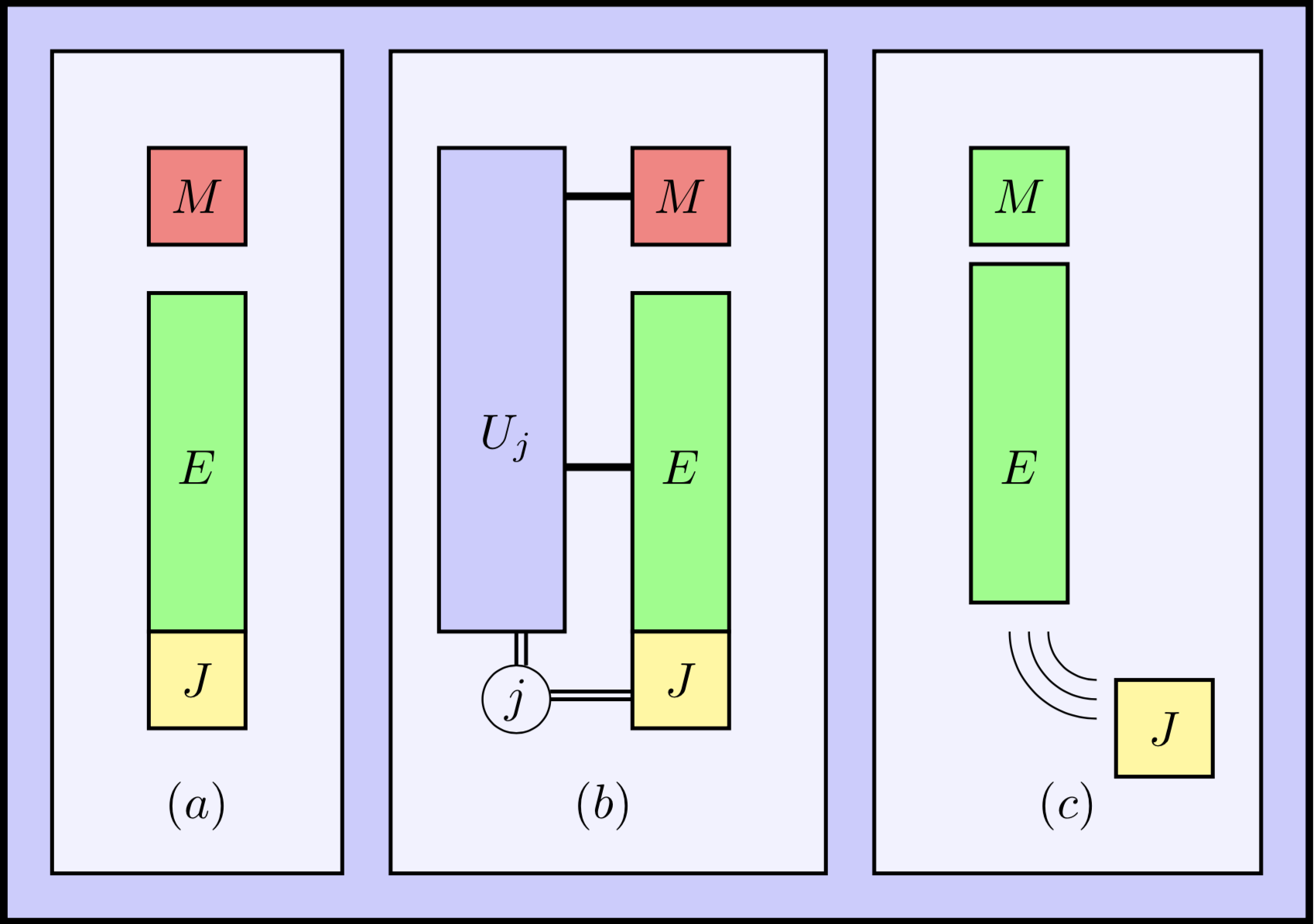
\Theta_{MEJ} = U (\rho_M\otimes\mu_{EJ}) U^\dagger.

\( (\epsilon, \log|J|)\)-catalytic erasure of \(\rho_M\) if \(\exists\) \(\sigma_M\in \mathcal{F}\) such that

\text{Pur}(\Theta_{ME}, \sigma_{M}\otimes \mu_E)\leq \epsilon

Let

\(\exists\) \((\epsilon+\delta, \log k)\)-catalytic erasure of \(\rho_{M}\), where 

Achievability

\log k := \min_{\sigma_{M}\in \mathcal{F}}D_{\max}^\epsilon(\rho_{M}\|\sigma_{M})+ 2\log\frac{1}{\delta}

One Sentence Proof:

Convex Splitting Lemma

For every \((\epsilon, \log|J|)\)- erasure of \(\rho_M\),

Converse

\log |J| \geq \min_{\sigma_M\in \mathcal{F}}D_{\max}^\epsilon(\rho_M\|\sigma_M)

Final Remarks

1. Works in the one-shot regime. 

2. Matching One-shot Bounds

Part II:

Distillation in General Resource Theory

[1] Madhav K. Vijayan, Eric Chitambar, and Min-Hsiu Hsieh,  arXiv:1906.04959.

​[2] Zi-Wen Liu, Kaifeng Bu, and Ryuji Takagi. Phys. Rev. Lett. 123, 020401 (2019)

One-shot distillation

\rho
\Phi_M
\Lambda \in \mathcal O
\epsilon

One-shot distillable rate

C_d(\rho, \epsilon) := \max\limits_{M \in \mathbb{N}} \left\lbrace \log_2 M : \max\limits_{\Lambda \in \mathcal{O}} F^2(\Lambda(\psi), \Phi_{M}) \geq 1- \epsilon \right\rbrace

It works for 

1. Free States form a convex and close set.

2. \Phi_M \gamma \Phi_M \leq \frac{1}{M} \Phi_M, \hspace{0.2cm} \forall \gamma \in \mathcal F
  • Entanglement
  • Coherence 
  • Purity
\checkmark
\checkmark
\checkmark

​[2] Zi-Wen Liu, Kaifeng Bu, and Ryuji Takagi. Phys. Rev. Lett. 123, 020401 (2019)

[1] Madhav K. Vijayan, Eric Chitambar, MH. J. Phys. A: Math. Theor. 51, 414001 (2018). [arXiv:1804.06554]

2. \Phi_M \gamma \Phi_M \leq \frac{1}{M} \Phi_M, \hspace{0.2cm} \forall \gamma \in \mathcal F
G_{min}(\rho) := \min\limits_{\gamma \in \mathcal F} \{ -\log \text{Tr}(\rho\gamma) \}
G_{min}(\Phi_M) \geq \log M

[Tuesday Morning: Julio de Vicente: A resource theory of entanglement with a unique multipartite maximally entangled state]

[1] Madhav K. Vijayan, Eric Chitambar, MH. J. Phys. A: Math. Theor. 51, 414001 (2018). [arXiv:1804.06554]

Main Result

C_d(\rho,\epsilon) \leq G_{min}^{2\sqrt \epsilon}(\rho)
\rho \hspace{0.1cm}- \hspace{-0.2cm} \rightarrow
\Lambda \in \mathcal{O}
\psi \hspace{0.1cm}- \hspace{-0.2cm} \rightarrow
\Lambda \in \mathcal{O}^{\tilde\epsilon}
\Phi_M
\epsilon
\Phi_M
\epsilon
G_{min}^{\epsilon}(\psi) \geq \log(1 + \mathcal R_f^{\tilde\epsilon}(\Phi_M))
C_d(\rho, \epsilon) \leq G^{2\sqrt{\epsilon}}_{min}(\rho)

Converse

G_{min}(\rho) := \min\limits_{\gamma \in \mathcal F} \{ -\log \text{Tr}(\rho\gamma) \}
GRT Entanglement Coherence

\(G_{min}(\rho)\)

\(S_{min}(\rho_\psi)\)

\(S_{min}(\Delta(\psi))\)

Proof Sketch

(2)\ \log M \leq \min\limits_{\gamma \in \mathcal{I}} \left\{ -\log_2\text{Tr}(\textcolor{red}{\overline{\rho}}\gamma) \right\}
\cdot \rho
\cdot \textcolor{red}{\overline{\rho}}
= G_{min}(\overline \rho)
2\sqrt{\epsilon}
(3)\ \forall \Lambda \in \mathcal O \text{ } s.t. \text{ } F^2(\Lambda(\rho), \Phi_M ) \geq 1 - \epsilon
(1)\ \Phi_M \Lambda(\gamma) \Phi_M \leq \frac{1}{M} \Phi_M \hspace{0.5cm} \forall \gamma \in \mathcal F
\overline{\rho} \text{ depends on } \Lambda, \Phi_M, \rho
G_{min}^{\epsilon}(\psi) \geq \log(1 + \mathcal R_f^{\tilde\epsilon}(\Phi_M))

Direct Coding

\mathcal R^{\tilde\epsilon}_f(\rho) := \min\limits_{\pi \in \mathcal F} \{ s \geq 0 : \frac{\rho + s \pi}{1 + s} \in \mathcal F^{\tilde\epsilon} \}
\exists \Lambda:\psi \mapsto \Phi_M

If

then

(1)\ \Lambda(\omega) = \text{Tr}(\overline\psi\omega)\phi + (1 - \text{Tr}(\overline\psi\omega))\pi_{\phi}
\pi_{\phi} \text{ optimizes } \mathcal R_f(\phi)

Proof Sketch

\overline \psi \text{ optimizes } G_{min}^{\epsilon}(\psi)
\cdot \phi
\cdot \textcolor{red}{\Lambda(\psi)}
{\epsilon}
\psi

[Tuesday: Julio de Vicente: A resource theory of entanglement with a unique multipartite maximally entangled state]

\text{If } \mathcal F \text{ is convex, } \Lambda \in \mathcal O, \text{ iff}
(1 - \text{Tr}(\overline\psi\gamma)) \geq \frac{ \mathcal R_f(\phi)}{1 + \mathcal R_f(\phi) } \hspace{0.1cm}\forall \gamma \in \mathcal F
\iff G_{min}^{\epsilon}(\psi) \geq \log(1 + \mathcal R_f(\phi))
(2)\ \Lambda(\omega) \in \mathcal{F}^{\tilde\epsilon}, \forall \omega \in\mathcal{F}

Part III:

Hierarchy of coherence operations

Hayata Yamasaki, Madhav Krishnan, Min-Hsiu Hsieh. In preparation.

Alexander Streltsov, Swapan Rana, Manabendra Nath Bera, and Maciej Lewenstein. Phys. Rev. X 7, 011024 (2017).

Main Result

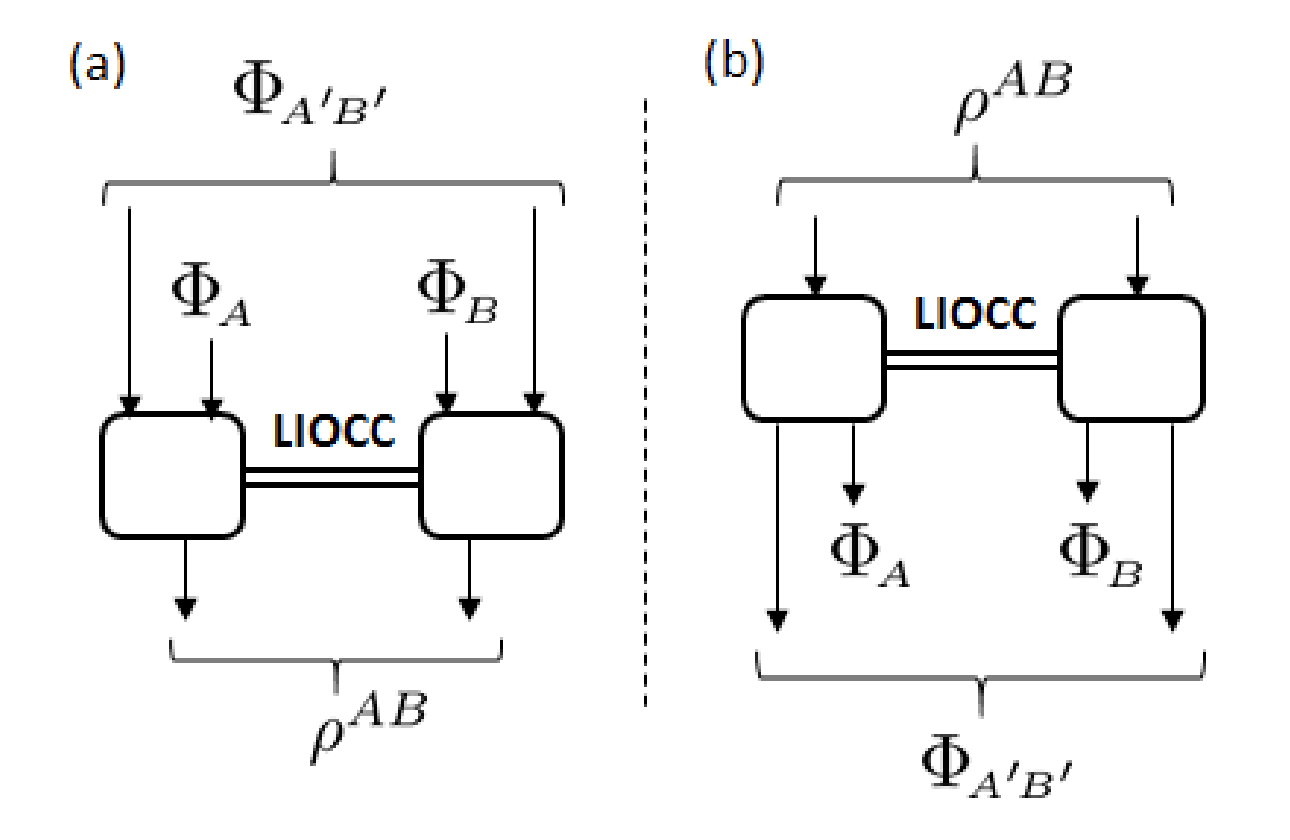
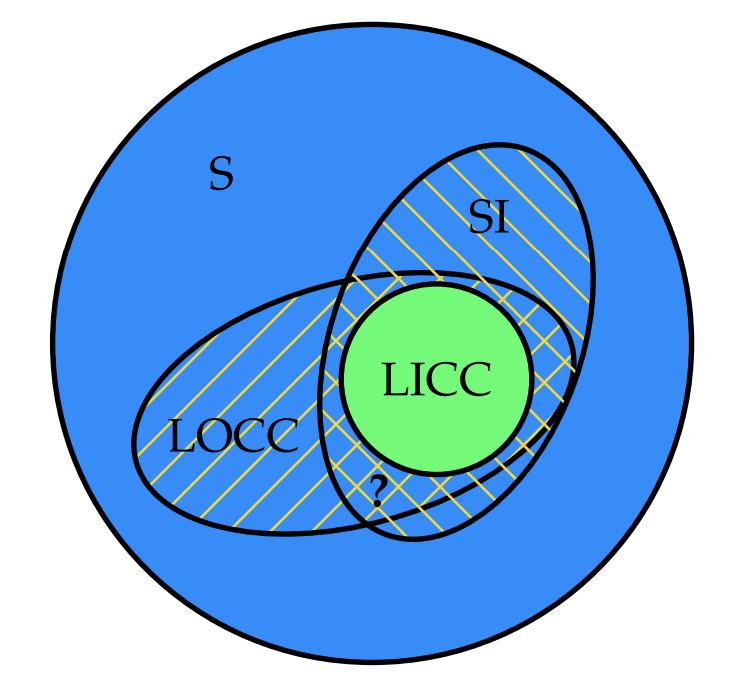
There is a strict separation between the set r-\(\mathsf{LICC}\)  and the set r-\(\mathsf{LOCC} \cap_{op} \mathsf{IO}\).

\mathcal{E}^{AB}\left(\rho^{AB}\right)\coloneqq\sum_{i=0}^{1}M_i\rho M_i^\dag,
M_1\coloneqq|-\rangle\langle-|^A\otimes Z^B,
M_0\coloneqq|+\rangle\langle+|^A\otimes I^B,

Example of 1-\(\mathsf{LOCC} \cap_{op} \mathsf{IO}\)

K_0\coloneqq \frac{I^A\otimes|0\rangle\langle0|^B+X^A\otimes|1\rangle\langle1|^B}{\sqrt{2}}
K_1\coloneqq\frac{X^A\otimes|0\rangle\langle0|^B+I^A\otimes|1\rangle\langle1|^B}{\sqrt{2}}

In the context of entanglement distillation.

r-\(\mathsf{LOCC} \cap_{op} \mathsf{IO}\) can distill one ebit, but r-\(\mathsf{LICC}\) cannot! 

Proof Idea

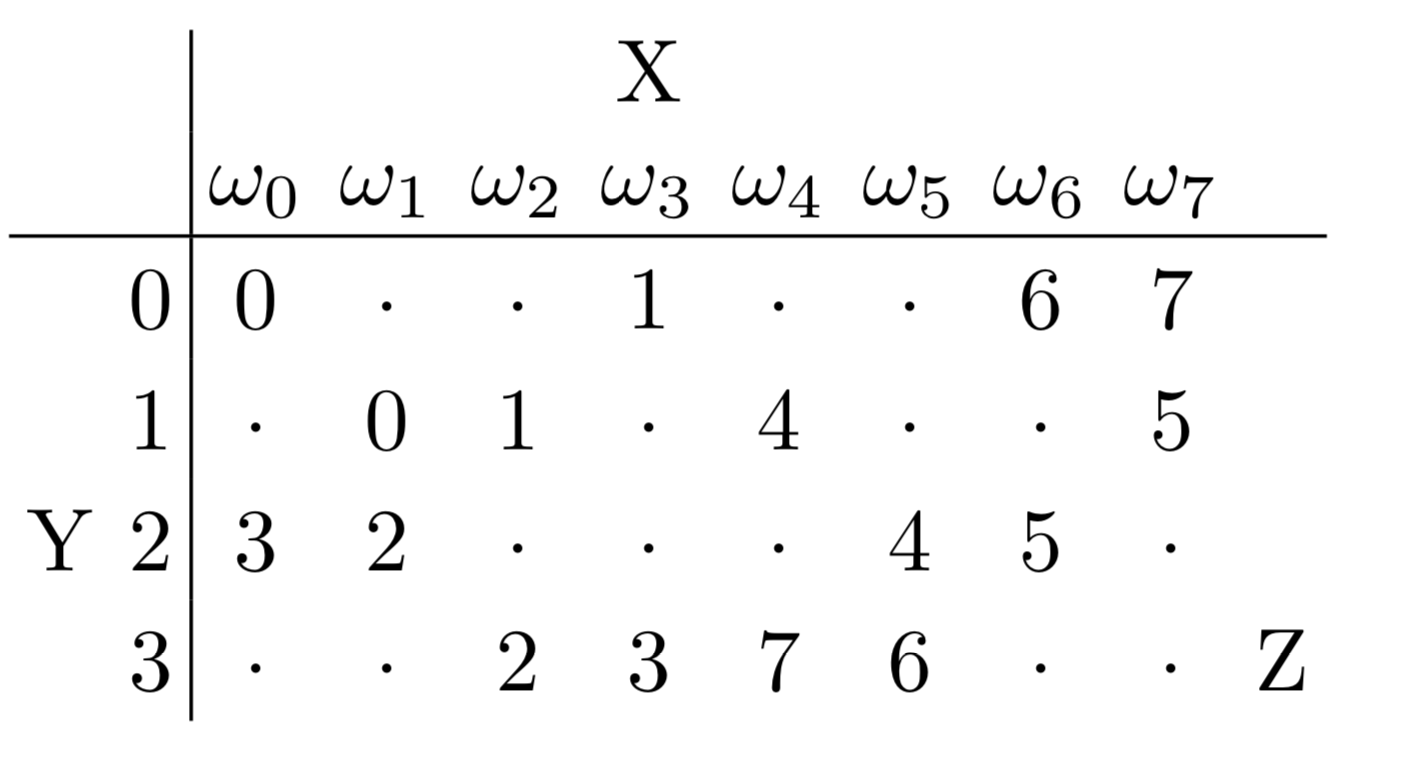
Eric Chitambar and Min-Hsiu Hsieh. Nature Communications 8, no. 2086 (2017).

K_0^A = |0\rangle\langle\omega_0|^A + |1\rangle\langle\omega_1|^A + |2\rangle\langle\omega_2|^A + |3\rangle\langle\omega_3|^A,
K_1^A = |4\rangle\langle\omega_4|^A + |5\rangle\langle\omega_5|^A + |6\rangle\langle\omega_6|^A + |7\rangle\langle\omega_7|^A.
L_0^B = \{|0\rangle\langle0|^B + |1\rangle\langle1|^B, |2\rangle\langle2|^B + |3\rangle\langle3|^B\},
L_1^B = \{|0\rangle\langle0|^B + |3\rangle\langle3|^B, |1\rangle\langle1|^B + |2\rangle\langle2|^B\}.

Alice's Measurement

Bob's Measurement

Free states remain free under these operations!

Impossibility of 2-LICC

1. Schmidt Rank cannot be increased under LICC.

2. Consider all possible choices of incoherent Kraus operators.

Thank you for your attention!

[2] Anurag Anshu, MH, Rahul Jain. Quantifying resource in catalytic resource theory. PRL vol. 121, p. 190504 (2018). [arXiv:1708.00381]

[1] Eric Chitambar, MH. Relating the Resource Theories of Entanglement and Quantum Coherence. PRL, vol. 117, p. 020402 (2016). [arXiv:1509.07458]

[4] Hayata Yamasaki, Madhav Krishnan Vijayan, MH. Hierarchy of quantum coherence operations. In preparation.

[3] Madhav Krishnan Vijayan, Eric Chitambar, MH. One-Shot distillation in a General Resource Theory. [arXiv:1906.04959]

Part IV:

Multipartite Inequivalent Coherence Classes 

[4] Yu Luo, Yongming Li, MH. Inequivalent Multipartite Coherence Classes and New Coherence Monotones. [arXiv:1807.06308].

How many are there for 3-qubit coherence states?

For 3 qubits, there are only two inequivalent entanglement classes under SLOCC.

There are already infinite many inequivalent coherence classes under SLICC for two qubits.

Main Result

# of product

terms

1
2
3
4
|00\rangle

Classification

a|00\rangle+b|01\rangle
a|00\rangle+b|10\rangle
a|00\rangle+b|11\rangle
a|00\rangle+b|01\rangle+c|10\rangle
a|00\rangle+b|01\rangle+c|11\rangle
a|00\rangle+b|01\rangle+c|10\rangle+d|11\rangle
\Delta= \frac{ad}{bc}

General Resource Theory

By Lawrence Min-Hsiu Hsieh

Made with Slides.com

General Resource Theory

Banff Conference. July 2019

  • 80

More from Lawrence Min-Hsiu Hsieh