Parameterized Quantum Circuits
Min-Hsiu Hsieh
(UTS)
and Its Applications in Machine Learning
Joint Work with
Yuxuan Du
Tongliang Liu
Dacheng Tao
(USyd)
Machine Learning Tasks




PQC Can Achieve


"In computational complexity-theoretic terms, this generally means providing a superpolynomial speedup over the best possible classical algorithm."
Quantum supremacy

QML applications are natural candidates for NISQ devices.
Part I
Parameterized Quantum
Circuits



and many more!

PQC
q(X)
\theta
Classical Optimization
Classical Optimization
\theta = \arg \min_{\bm{\theta}} \mathcal{L}(q(X),p(X))
Given an loss function \(\mathcal{L}\), PQC output \(q(X)\), a target distribution \(p(X)\),
Part II
PQC as Quantum Perceptron



and more!

Quantum Perceptron
Grover Search
P_\omega= |\omega\rangle\langle \omega|
P_s= |+\rangle\langle +|^{\otimes n}
U_s= 2|+\rangle\langle +|^{\otimes n} - I
U_\omega= 2|\omega\rangle\langle \omega| - I
How to identify
from
Grover Search

Variational Grover Search
\min_{\phi} \langle \phi |P_{\omega^\perp} | \phi\rangle
Learn \(|\phi\rangle\) using trainable quantum circuits.
Morales, Tlyachev, and Biamonte. Variationally Learning Grover’s Quantum Search Algorithm. arXiv:1805.09337
U(\alpha) = e^{i\alpha P_\omega}
V(\beta) = e^{i\beta P_s}
Variational Grover Search

Variational Quantum Perceptron

Variational Quantum Perceptron
\mathcal{D} = \{\bm{x}_i \in \mathbb{R}^M, y_i\in\{\pm 1\}\}_{i=1}^N
|\Phi^{(k)}\rangle_{F,I}= U_{data}(\mathcal{D})
=\frac{1}{\sqrt{N}}\left(\sum_{i=0,i\neq k}^{N-1}|\psi_i^{(0)}\rangle_{F}|i\rangle_I -|\psi_k^{(1)}\rangle_{F}|k\rangle_I\right).
Variational Quantum Perceptron
U_{c1}|\Phi^k\rangle_{F,I}=|\varphi\rangle_F\otimes\left(\cos3\theta|B\rangle_I+\sin3\theta|k\rangle_I\right)
U_{L_1}|{\Phi^k}\rangle_{F,I}= \cos\theta(\textcolor{red}{\alpha_B}|\psi_B^{(0)}\rangle_F+ \textcolor{green}{\beta_k}|\psi_k^{(1)}\rangle_F)|{B}\rangle_I + \sin\theta(-\textcolor{red}{\alpha_B}|\psi_B^{(0)}\rangle_F+ \textcolor{green}{\beta_k}|\psi_k^{(1)}\rangle_F)|{k}\rangle_I
VQP Performance

N=16, M=4
Performance
N=16, M=4

Quantum Ensemble Learning
Combine weak VQP \(\{V_t\}\) into strong classifier \(\rm{sign}(\sum_t |y_t - C_T|)\).
Required significant smaller size of training sets
QEL Complexity
Query Complexity \(O(\textcolor{red}{T}\text{poly}(\log M\textcolor{green}{\sqrt{\log N}}))\).
Runtime \(O(\text{poly}(\log M \log( M\sqrt{\log N}))\sqrt{\log N})\).
If \(|\mathcal{D}_t|\approx \log {N} \)
QEL Performance
\( \mathcal{D}=\{\bm{x}_i,y_i\}_{i=1}^{10000} \)
\( \mathcal{D}_i=\{\bm{x}_k,y_k\}_{k=1}^{8} \)

Gate Count
\( \mathcal{D}=\{\bm{x}_i,y_i\}_{i=1}^{10000} \)
\( \mathcal{D}_i=\{\bm{x}_k,y_k\}_{k=1}^{8} \)
Encoding requires 29 single and two qubits gates.
QEL requires 48 parameterized single qubit gates, 8 CNOT gates, 12 NOT gates, 20 Hadamard gates, and 10 Toffoli gates.
Total of 248 single and two-qubit gates.
Thank you for your attention!
Part III
The Expressive Power of Parameterized Quantum Circuits
What is the generative power of parametrized quantum circuits?

MPQC
- arXiv:1801.07686, arXiv:1804.04168
TPQC

arXiv:1803.11537
Boltzmann Machine

Boltzmann Machine

MPQC\(>\)DBM\(>\)TPQC\(>\)RBM
Expressive Power:

IQP circuits
MPQC\(>\)DBM

IQP Circuit Can be simulated by MPQCs with the following arrangement.
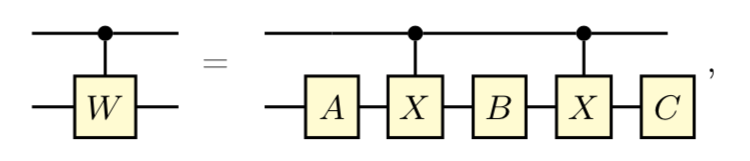

DBM\(>\)TPQC

TPQC\(>\)RBM
TPQC can generate entangled state with volume law (Bond Dimension \(O(D^N)\)).
RBM Cannot!
-
Gao and Duan, Nature Communications 8, 662 (2017).
-
Chen et. al., Physical Review B 97, 085104 (2018).
MPQC with Post-Selection

MPQC with post-selection can simulate General Tensor Networks.


Part VI
Quantum Divide-and-Conquer GAN

Seth Lloyd and Christian Weedbrook. "Quantum generative adversarial learning". Phys. Rev. Lett. 121, 040502 (2018)

Generative Adversarial Network

Parameterized Quantum Circuits
By Lawrence Min-Hsiu Hsieh
Parameterized Quantum Circuits
The Second Hong Kong - Shenzhen Workshop on Quantum Information Science
- 914



