Parameterized Quantum Circuits
Min-Hsiu Hsieh
(UTS)
and Its Applications in Machine Learning
Joint Work with
Yuxuan Du
Tongliang Liu
Dacheng Tao
(USyd)
Machine Learning Tasks
PQC Can Achieve
"In computational complexity-theoretic terms, this generally means providing a superpolynomial speedup over the best possible classical algorithm."
Quantum supremacy
QML applications are natural candidates for NISQ devices.
Part I
Parameterized Quantum
Circuits
and many more!
PQC
q(X)
\theta
Classical Optimization
Classical Optimization
\theta = \arg \min_{\bm{\theta}} \mathcal{L}(q(X),p(X))
Given an loss function \(\mathcal{L}\), PQC output \(q(X)\), a target distribution \(p(X)\),
Part II
PQC as Quantum Perceptron
and more!
Quantum Perceptron
Grover Search
P_\omega= |\omega\rangle\langle \omega|
P_s= |+\rangle\langle +|^{\otimes n}
U_s= 2|+\rangle\langle +|^{\otimes n} - I
U_\omega= 2|\omega\rangle\langle \omega| - I
How to identify
from
Grover Search
Variational Grover Search
\min_{\phi} \langle \phi |P_{\omega^\perp} | \phi\rangle
Learn \(|\phi\rangle\) using trainable quantum circuits.
Morales, Tlyachev, and Biamonte. Variationally Learning Grover’s Quantum Search Algorithm. arXiv:1805.09337
U(\alpha) = e^{i\alpha P_\omega}
V(\beta) = e^{i\beta P_s}
Variational Grover Search
Variational Quantum Perceptron
Variational Quantum Perceptron
\mathcal{D} = \{\bm{x}_i \in \mathbb{R}^M, y_i\in\{\pm 1\}\}_{i=1}^N
|\Phi^{(k)}\rangle_{F,I}= U_{data}(\mathcal{D})
=\frac{1}{\sqrt{N}}\left(\sum_{i=0,i\neq k}^{N-1}|\psi_i^{(0)}\rangle_{F}|i\rangle_I -|\psi_k^{(1)}\rangle_{F}|k\rangle_I\right).
Variational Quantum Perceptron
U_{c1}|\Phi^k\rangle_{F,I}=|\varphi\rangle_F\otimes\left(\cos3\theta|B\rangle_I+\sin3\theta|k\rangle_I\right)
U_{L_1}|{\Phi^k}\rangle_{F,I}= \cos\theta(\textcolor{red}{\alpha_B}|\psi_B^{(0)}\rangle_F+ \textcolor{green}{\beta_k}|\psi_k^{(1)}\rangle_F)|{B}\rangle_I + \sin\theta(-\textcolor{red}{\alpha_B}|\psi_B^{(0)}\rangle_F+ \textcolor{green}{\beta_k}|\psi_k^{(1)}\rangle_F)|{k}\rangle_I
VQP Performance
N=16, M=4
Performance
N=16, M=4
Quantum Ensemble Learning
Combine weak VQP \(\{V_t\}\) into strong classifier \(\rm{sign}(\sum_t |y_t - C_T|)\).
Required significant smaller size of training sets
QEL Complexity
Query Complexity \(O(\textcolor{red}{T}\text{poly}(\log M\textcolor{green}{\sqrt{\log N}}))\).
Runtime \(O(\text{poly}(\log M \log( M\sqrt{\log N}))\sqrt{\log N})\).
If \(|\mathcal{D}_t|\approx \log {N} \)
QEL Performance
\( \mathcal{D}=\{\bm{x}_i,y_i\}_{i=1}^{10000} \)
\( \mathcal{D}_i=\{\bm{x}_k,y_k\}_{k=1}^{8} \)
Gate Count
\( \mathcal{D}=\{\bm{x}_i,y_i\}_{i=1}^{10000} \)
\( \mathcal{D}_i=\{\bm{x}_k,y_k\}_{k=1}^{8} \)
Encoding requires 29 single and two qubits gates.
QEL requires 48 parameterized single qubit gates, 8 CNOT gates, 12 NOT gates, 20 Hadamard gates, and 10 Toffoli gates.
Total of 248 single and two-qubit gates.
Part III
The Expressive Power of Parameterized Quantum Circuits
What is the generative power of parametrized quantum circuits?
MPQC
- arXiv:1801.07686, arXiv:1804.04168
TPQC
arXiv:1803.11537
Boltzmann Machine
Boltzmann Machine
MPQC\(>\)DBM\(>\)TPQC\(>\)RBM
Expressive Power:
IQP circuits
MPQC\(>\)DBM
IQP Circuit Can be simulated by MPQCs with the following arrangement.
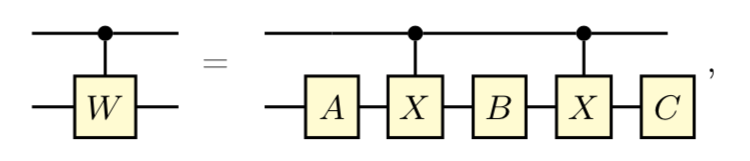
DBM\(>\)TPQC
TPQC\(>\)RBM
TPQC can generate entangled state with volume law (Bond Dimension \(O(D^N)\)).
RBM Cannot!
-
Gao and Duan, Nature Communications 8, 662 (2017).
-
Chen et. al., Physical Review B 97, 085104 (2018).
MPQC with Post-Selection
MPQC with post-selection can simulate General Tensor Networks.
Part VI
Quantum Divide-and-Conquer GAN
Seth Lloyd and Christian Weedbrook. "Quantum generative adversarial learning". Phys. Rev. Lett. 121, 040502 (2018)
Generative Adversarial Network
Thank you for your attention!
Parameterized Quantum Circuits
By Lawrence Min-Hsiu Hsieh
Parameterized Quantum Circuits
arXiv:1809.06056+1810.11922
