Functional programming
Imperative
vs
Declarative programming
U = IR
What language is functional?
Main things
- Function is a first-class and higher-order citizen
- Pure functions
- Recurtion
- Algebraic data types
- Strict versus non-strict evaluation (nice to have)
main = map (\x -> 3 * x + 1) [1, 2, 3, 4, 5]const fn = arr => (prop, asc) => arr.slice().sort((a, b) => {
return asc * (a[prop] > b[prop] ? 1 : (a[prop] === b[prop] ? 0 : -1));
});
const sorter = fn([{a: 1}, {a: 2}, {a: 3}]);
// a lot of lines after
sorter("a", 1);
// a few more lines of code
sorter("a", -1);Pure functions
function fn (a, b) {
console.log(a, b);
return a + b;
}Math.random()Date.now()main = let a = 3
b = 1
in map (\x -> a * x + b) [1, 2, 3, 4, 5]const fn = arr => (prop, asc) => arr.slice().sort((a, b) => {
return asc * (a[prop] > b[prop] ? 1 : (a[prop] === b[prop] ? 0 : -1));
});function () {
let hash = {
// some data
};
return function (item) {
return hash[item.id];
}
}function () {
let hash = {
// some data
};
return function (item) {
if (!hash[item.id]) {
hash[item.id] = item;
}
return hash[item.id];
}
}Recurtion

There are no loops
function factorial(x) {
if (x <= 0) {
return 1;
} else {
return x * factorial(x-1); // (A)
}
}
factorial(100000);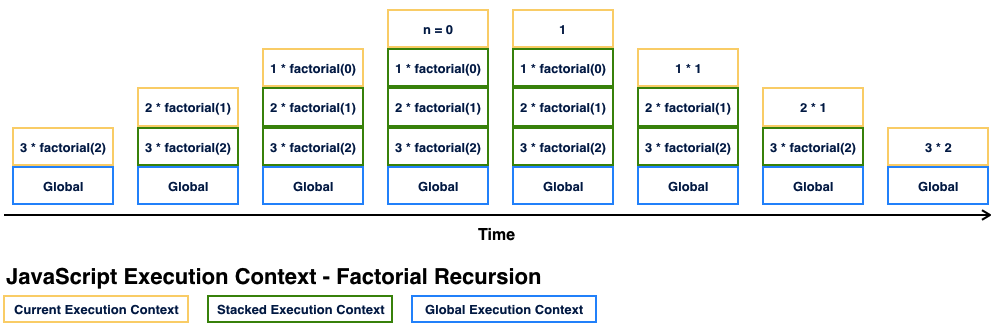
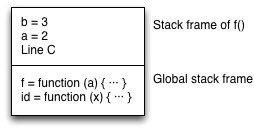
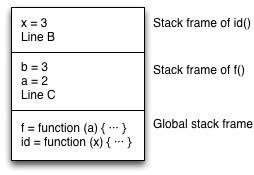
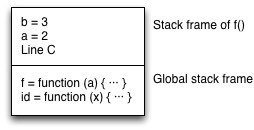
Tail call optimizations
function id(x) {
return x; // (A)
}
function f(a) {
let b = a + 1;
return id(b); // (B)
}
console.log(f(2)); // (C)
C
B
A
B

C
Tail call
function id(x) {
return x; // (A)
}
function f(a) {
let b = a + 1;
return id(b); // (B)
}
console.log(f(2)); // (C)
C

B

A
What can be optimized?
const a = x => x ? f() : g();const a = () => f() || g();const a = () => f() && g();const a = () => (f() , g());function foo() {
bar();
}function foo() {
bar();
return undefined;
}function factorial(x) {
if (x <= 0) {
return 1;
} else {
return x * factorial(x-1); // (A)
}
}function factorial(n) {
return facRec(n, 1);
}
function facRec(x, acc) {
if (x <= 1) {
return acc;
} else {
return facRec(x-1, x*acc); // (A)
}
}Why?
function a() { return b() }
function b() { return c() }
function c() { console.trace() ..// would not include b()!Algebraic data types

Types are also functions
data Bool = False | Truedata List a = Nil
| Cons a (List a)data Type :: * -> * where
Char :: Type Char
Int :: Type Int
List :: Type a -> Type [a]sum :: Type a -> a -> Int
sum Char _ = 0
sum Int n = n
sum (List a) xs = foldr (+) 0 (map (sum a) xs)f :: Int -> Int
f 0 = 1
f 1 = 5
f 2 = 2
f _ = -1map _ [] = []
map f (x:xs) = f x : map f xshello :: Pet -> String
hello x =
case x of
Cat -> "meeow"
Dog -> "woof"
Fish -> "bubble"Strict versus non-strict evaluation
print length([2+1, 3*2, 1/0, 5-4])How we can do?
Immutable data structures
Category theory
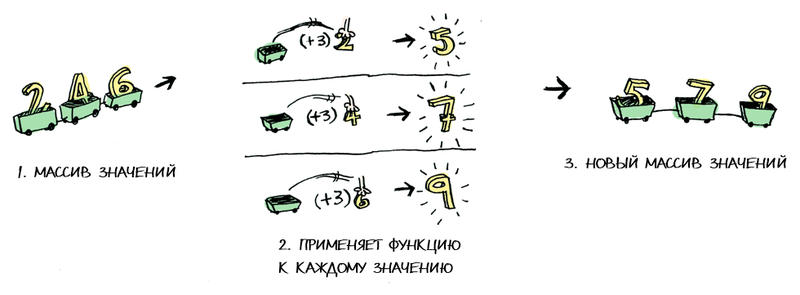
Functor

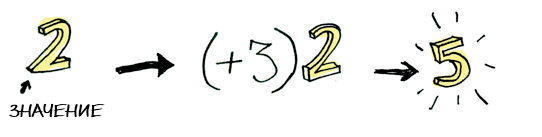
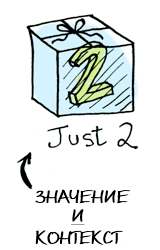
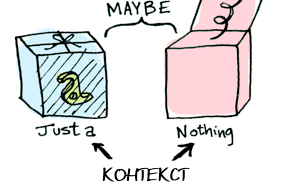
data Maybe a = Nothing | Just a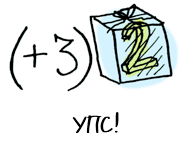
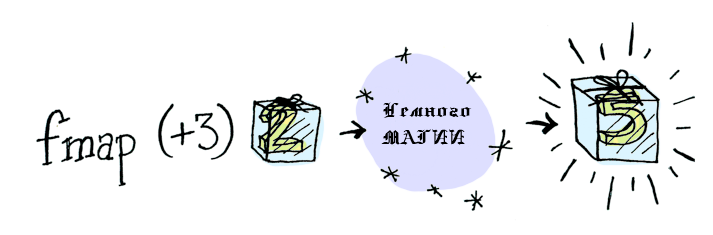
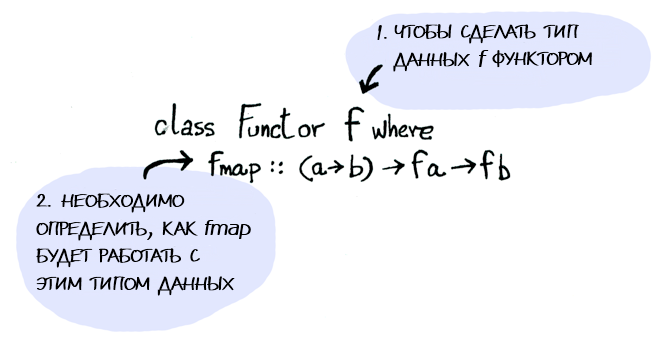
Функтор — это класс типов.
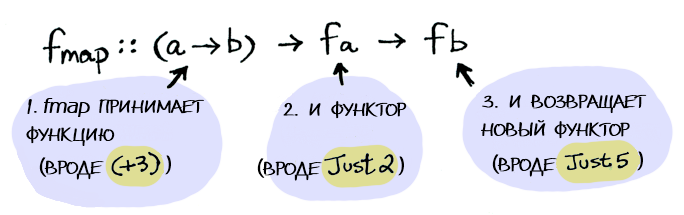
> fmap (+3) (Just 2)
Just 5instance Functor Maybe where
fmap func (Just val) = Just (func val)
fmap func Nothing = Nothing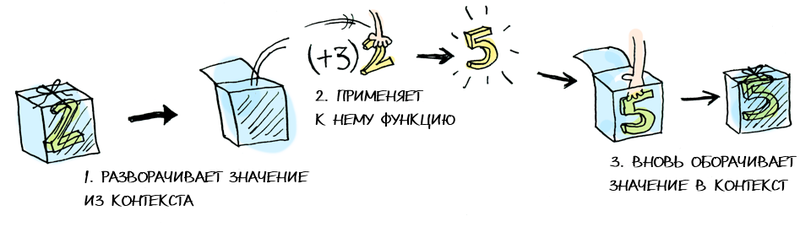
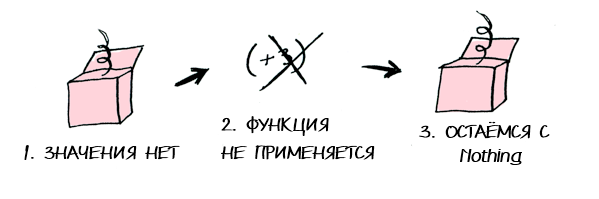
post = Post.find_by_id(1)
if post
return post.title
else
return nil
endgetPostTitle <$> (findPost 1)Example of Functor?
what if?
fmap (+3) (+1)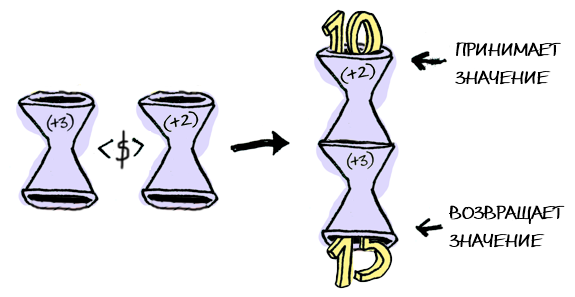
> import Control.Applicative
> let foo = fmap (+3) (+2)
> foo 10
15Applicatives

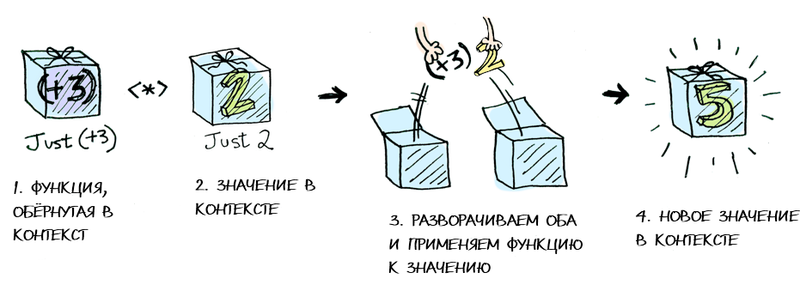
Just (+3) <*> Just 2 == Just 5> (+) <$> (Just 5)
Just (+5)
> Just (+5) <$> (Just 4)> (+) <$> (Just 5)
Just (+5)
> Just (+5) <*> (Just 3)
Just 8> (*) <$> Just 5 <*> Just 3
Just 15Monads
half x = if even x
then Just (x `div` 2)
else Nothing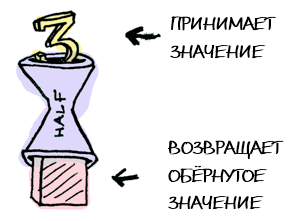

Monad — ещё один класс типов
class Monad m where
(>>=) :: m a -> (a -> m b) -> m b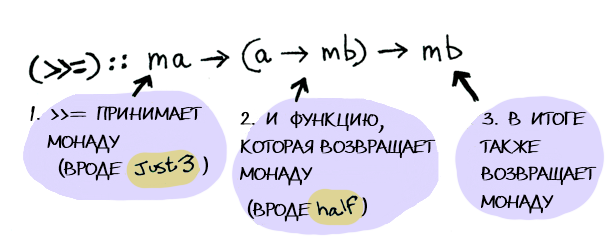
instance Monad Maybe where
Nothing >>= func = Nothing
Just val >>= func = func val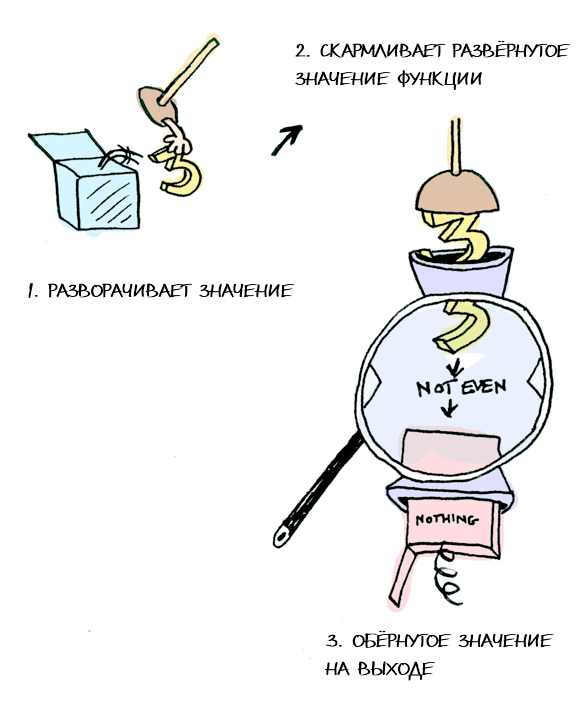
> Just 20 >>= half >>= half >>= half
Nothing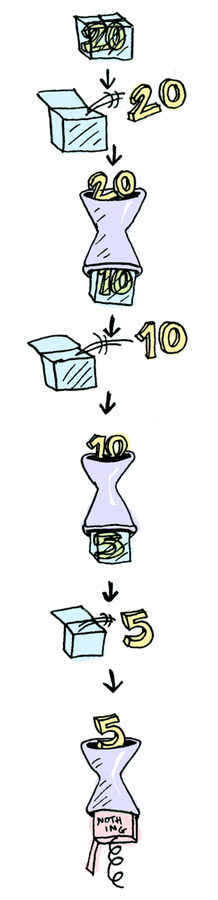
IO монада



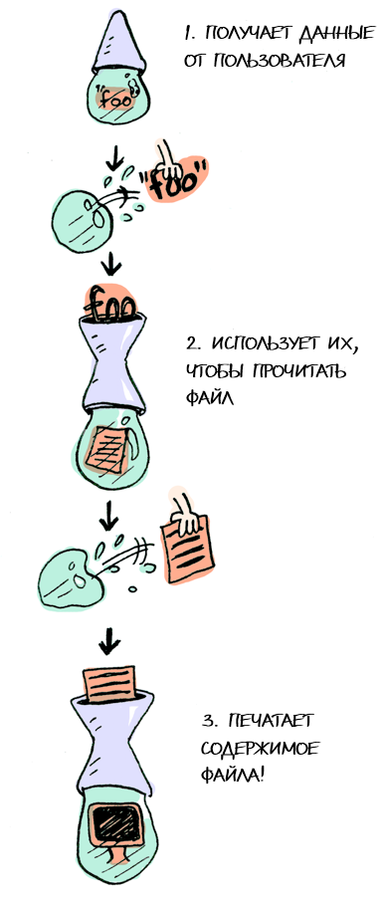
getLine >>= readFile >>= putStrLnQuestions?
Functional programming
By Vladimir
Functional programming
- 245



