樹論
linki
kumokunn
Ranger
一點名詞
以1為根
1為2的父親
2為5的父親
.......
1
2
4
5
3
6
以1為根
2為1的小孩
4、5為2的小孩
.......
1
2
4
5
3
6
可觀察出每個點只會有一個父親
但可以有數個小孩
祖先:
父親
父親的父親
父親的父親的父親
......
根節點
4的祖先有1、2(1為根節點)
1
2
4
5
3
6
深度(degree)
某個節點到根節點的最短距離
深度0
深度2
深度1
1
2
4
5
3
6
子樹
1
2
4
5
3
6
樹重心
特殊的點
以他為根時
子樹大小\(<=\frac{n}{2}\)
可能有1~2個
2個時兩重心相鄰
1
2
4
5
3
6
重心
樹直徑
樹中最長的不重複路徑
1
2
4
5
3
6
葉子
只有父親沒有兒子
1
2
4
5
3
6
樹直徑
作法
- 從任意點開始DFS
- 找到此次DFS中最遠的點
- 從那個點開始DFS
- 此時最遠的距離為樹直徑,
起點與終點為樹直徑兩端點
\(O(N)\)
1
2
4
5
3
6
起點
端點A
端點B
證明
left as an exercise for reader
題目
樹重心
方法
- 照定義算子樹大小
- greedy找
\(O(N)\)
照定義扣
void dfs(int pos,int pre){
sub[pos]=1;
wei[pos]=0;
for(auto i:dis[pos]){
if(i!=pre){
dfs(i,pos);
sub[pos]+=sub[i];
wei[pos]=max(wei[pos],sub[i]);
}
}
wei[pos]=max(wei[pos],n-sub[pos]);
if(wei[pos]<=n/2){
if(centroid[0]==0){
centroid[0]=pos;
}else centroid[1]=pos;
}
}greedy扣
int DFS_cen(int u, int pa) {
for (int v : G[u]) {
if (vis[v] || v == pa) continue;
if (siz[v] * 2 > siz[u])return DFS_cen(v, u);
}
return u;
}題目
LCA
樹上最低共同祖先
1
2
4
5
3
6
LCA
1
2
4
5
3
6
LCA
1
2
4
5
3
6
LCA
做法
-
倍增
-
樹壓平+RMQ(樹壓平講
初始化\(O(NlogN)\)查詢\(O(logN)\)
倍增做法
- DFS預處理父親、深度
- sprase table預處理2倍祖先、4倍祖先....
- 將兩個點跳到同深度
- 倍增求解
倍增想法
跳到同深度後
你發現再往上跳時有單調性
但你又不能用一般的二分搜
於是你用倍增
1
2
4
5
3
6
函數:往上跳x步後
同一個點回傳1
不同回傳0
| 步數 | 0 | 1 | 2 | 3 |
| 回傳值 | 0 | 1 | 1 | 1 |
跳法
從最大步的開始試
若跳完點不一樣就跳
反之則不跳
全部跳完後再往上跳一步
正確性
將答案視為跳\(x\)次後是LCA
有\(\Sigma^{n-1}_{k=0}2^k<2^n\)的性質
可知道當跳了還不是相同點時一定要跳
不然之後不可能會到LCA
反之可能超過LCA
扣的
int lca(int a,int b){
if(dep[a]>dep[b])swap(a,b);
int jump=dep[b]-dep[a];
for(int i=0;i<=ma;i++){
if(jump&(1<<i))b=rmq[b][i];
}
if(a==b)return a;
for(int i=ma;i>=0;i--){
if(rmq[a][i]!=rmq[b][i]){
a=rmq[a][i];b=rmq[b][i];
}
}
return rmq[a][0];
}*記得把跟節點的祖先設為自己
題目
樹壓平(樹序列化
左圖為資訊社長對
炒飯做樹壓平
可以有效降低炒飯溫度

把樹壓平 怎麼壓?
扣的
void dfs(int pos,int pre){
arr[cnt++]=pos;
for(auto i:gra[pos]){
if(pos!=pre){
dfs(i);
}
}
arr[cnt++]=pos;
}\(O(N)\)
1
2
4
5
3
6
5
4
2
1
12
10
9
11
8
7
6
5
4
3
2
1
6
6
3
2
1
4
5
3
另一種扣的
void dfs(int pos,int pre){
arr[cnt++]=pos;
for(auto i:gra[pos]){
if(pos!=pre){
dfs(i,pos);
arr[cnt++]=pos;
}
}
}1
2
4
5
3
6
5
4
2
1
8
9
7
6
4
3
2
1
6
3
2
1
2
3
1
10
11
5
特色
對一個點\(u\)來說
他的子樹中的點\(v\)會有
\(Tin_u<Tin_v,Tout_u>Tin_v\)
可以以此性質搭配區間操作
來對子樹做事
例題
用第二種的寫法可以算LCA
void dfs(int pos,int pre){
arr[cnt++]=pos;
for(auto i:gra[pos]){
if(pos!=pre){
dfs(i);
arr[cnt++]=pos;
}
}
}兩個點的LCA是他們在序列中位置間
深度最小的
題目們
樹上啟發式合併
每個節點有一個set(或是其他資結
合併時用小的合到大的上
1
2
3
此時每個元素最多複製\(log(n)\)次
最多有\(O(nlog(n))\)個操作
原因樹鏈剖分一起講
題目
樹DP
在樹上做DP
通常會記錄一些東西
加上DFS
樹前綴
節點到根節點的所有節點和
扣的
void dfs(int pos,int pre){
for(auto i:gra[pos]){
if(i!=pre){
dp[i]+=dp[pos];
dfs(i,pos);
}
}
}\(O(N)\)
題目
全方位木DP
當題目問你以不同節點為根中最好的解
用DP全部跑跑看
又稱換根DP
實際操作
額外記錄一些東西
在DFS時想辦法讓節點DP值可由其他節點推導
全方位木DP需要你可以快速做到這件事
樹鏈剖分
a.k.a.輕重鏈剖分、HLD
把節點與子樹最大的兒子連起來
1
2
4
5
3
6
重鍊
輕鍊
輕鍊
重鍊
目標
可以在樹上使用區間資結
(BIT、線段樹)
步驟
- dfs找子樹大小
- hld函式建立輕重鍊(定義
並依遍歷順序來建立序列 - query時跳鍊(跳到LCA)
建立\(O(N)\) 查詢\(O(logN)\)
查詢時會跳到鍊的最上面
在往上跳到另一條鍊
此時跳到鍊的最上面為\(O(1)\)
然後最多跳\(logN\)條
因為跳鍊相當於從輕鍊往上跳
輕鍊最大是子樹的一半
建立
1
2
4
5
3
6
5
4
2
1
6
5
4
3
2
1
6
3
LCA
1
2
4
5
3
6
5
4
2
1
6
5
4
3
2
1
6
3
LCA
一些實作細節
要記每條鍊深度最低的節點
每個點的父親
每個點在序列上的位置
跳鍊時跳鍊的最上面較深的點(?
void dfs_siz(int pos,int pre){
siz[pos]=1;
for(auto i:edg[pos]){
if(i!=pre){
dep[i]=dep[pos]+1;
dfs_siz(i,pos);
siz[pos]+=siz[i];pr[i]=pos;
}
}
}
void hld(int pos,int pre,int tp){
in[pos]=cnt++;top[pos]=tp;
int hchi=-1,hsiz=-1;
for(auto i:edg[pos]){
if(i!=pre)if(hsiz<siz[i]){
hsiz=siz[i];hchi=i;
}
}
if(hchi==-1)return;
hld(hchi,pos,tp);
for(auto i:edg[pos]){
if(i!=pre&&i!=hchi)hld(i,pos,i);
}
return;
}
int path(int a,int b){
int ans=0;
while(top[a]!=top[b]){
if(dep[top[a]]>dep[top[b]])swap(a,b);
ans=max(ans,query(1,1,n,in[top[b]],in[b]));
b=pr[top[b]];
}
if(dep[a]>dep[b])swap(a,b);
ans=max(ans,query(1,1,n,in[a],in[b]));
return ans;
}我的扣
題目
重心分治
當你想不到要怎麼辦的時候
對樹套分治
基本型態:
利用重心把樹分成數個子樹
在遞迴求解,此時因重心特性
最差時
\(T(N)=2T(\frac{N}{2})+f(N)\)
\(f(n) \in O(n)\)時\(T(N) \in O(NlogN)\)
常要維護一些東西和在遞迴過程中額外計算
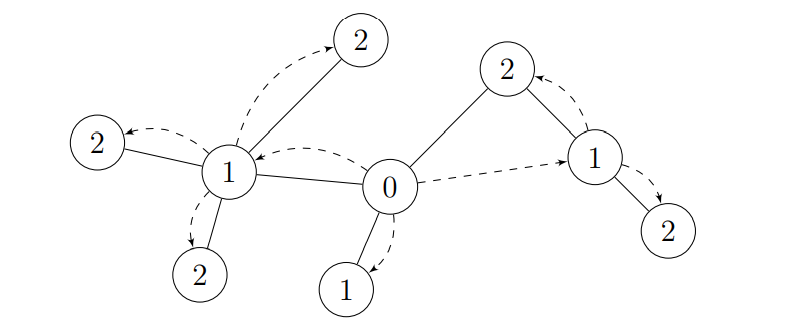
重心樹
扣的
void centroid_decomp(int node = 1) {
int centroid = get_centroid();
processed[centroid] = true;
for (int i : graph[centroid]) if (!processed[i]) centroid_decomp(i);
}學長的模板
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1E5+10;
vector<int> G[MAXN];
int sz[MAXN], centree[MAXN];
//centree[x] = 重心樹上的父節點
bool visited[MAXN];
void getsz(int x, int f){
sz[x]=1;
for(int i:G[x]){
if(visited[i]||i==f) continue;
getsz(i,x);
sz[x]+=sz[i];
}
}
int findcentroid(int x, int f, int s){
for(int i:G[x]){
if(2*sz[i]>=s&&i!=f&&!visited[i]){
return findcentroid(i,x,s);
}
}
return x;
}
void getcentree(int x, int f){
getsz(x,f);
int cent=findcentroid(x,f,sz[x]);
centree[x]=f;
visited[cent]=1;
for(int i:G[cent]){
if(!visited[i]) getcentree(i,cent);
}
}題目
樹上二分圖最小點覆蓋
題單
樹論
By linki1010111
樹論
- 693



