Tomography on Continuous Variable Quantum Systems
Ludmila Augusta Soares Botelho
Departamento de Física - ICEx - Universidade Federal de Minas Gerais
Representations
Discrete
Continuous
Experiment
Data
Quantum Mechanics
Data
Quantum State
Representations
Discrete
Continuous
Quantum States
Discrete
Continuous
\vert \uparrow \rangle = \begin{bmatrix}
1\\
0\\
\end{bmatrix}
\vert \downarrow \rangle = \begin{bmatrix}
0\\
1\\
\end{bmatrix}
\vert 0 \rangle = \begin{bmatrix}
1\\
0\\
\end{bmatrix}
\vert 1 \rangle = \begin{bmatrix}
0\\
1\\
\end{bmatrix}
Phase Space
- Wigner Function
$$W(q,p) = \frac{1}{2\pi\hbar} \int \left\langle q-\frac{v}{2}\right\vert \rho\left\vert q+\frac{v}{2}\right\rangle e^{ipv/\hbar}\mathrm{d}v$$
- Allows Negative Values
- Quasi-probability
Homodyne Detection
2-1
$$\vert \alpha \rangle$$
signal
50/50
Intensity Photon number
$$I_{21} = I_1 - I_2$$
$$ \propto$$
\hat{n}_1=\hat{a}_1'^\dagger\hat{a}_1' \qquad \hat{n}_2=\hat{a}_2'^\dagger\hat{a}_2'\\
\hat{a}_1'=2^{1/2}(\hat{a}'-\alpha_{LO}) \qquad \hat{a}_2'=2^{1/2}(\hat{a}'+\alpha_{LO}) \\
\hat{n}_{21} = \hat{n}_{2} - \hat{n}_{1} = \alpha_{LO}^*\hat{a}+\alpha_{LO}\hat{a}^{\dagger} \\
\alpha = \vert\alpha_{LO}\vert(\cos{\theta} +i\sin{\theta}) \\
\hat{n}_{21} = \frac{1}{\sqrt{2}} \vert{\alpha_{LO}}\vert \left[ (\cos{\theta} +i\sin{\theta})(\hat{q} - i\hat{p}) + (\cos{\theta} +i\sin{\theta})(\hat{q} - i\hat{p}) \right]\\
\hat{n}_{21} = \frac{2}{\sqrt{2}}\vert{\alpha_{LO}}\vert\hat{q}_{\theta}
\langle{q_{\theta}}\vert\rho \vert{q_{\theta}}\rangle = \frac{1}{2\pi\hbar} \int_{-\infty}^{\infty} W(q_{\theta}\cos{\theta} - p_{\theta}\sin{\theta},q_\theta \sin{\theta} + p_{\theta}\cos{\theta}) \mathrm{d}p_{\theta}
Radom Transform
$$\langle{q_{\theta}}\vert\rho \vert{q_{\theta}}\rangle \rightarrow W(q,p)$$
$$W(q,p) \rightarrow \langle{q_{\theta}}\vert\rho \vert{q_{\theta}}\rangle $$
?
W(q,p) = \frac{1}{2 \pi^{2}} \int_{-\infty}^{+\infty} \int_{0}^{\pi} pr(x,\theta) K(q\cos{\theta} + p\sin{}\theta -x) \mathrm{d}x \mathrm{d}\theta
Inverse Radom
K(x)= \frac{1}{2} \int_{-\infty}^{+\infty} \vert{\xi}\vert \exp{(i\xi x)} \mathrm{d}\xi
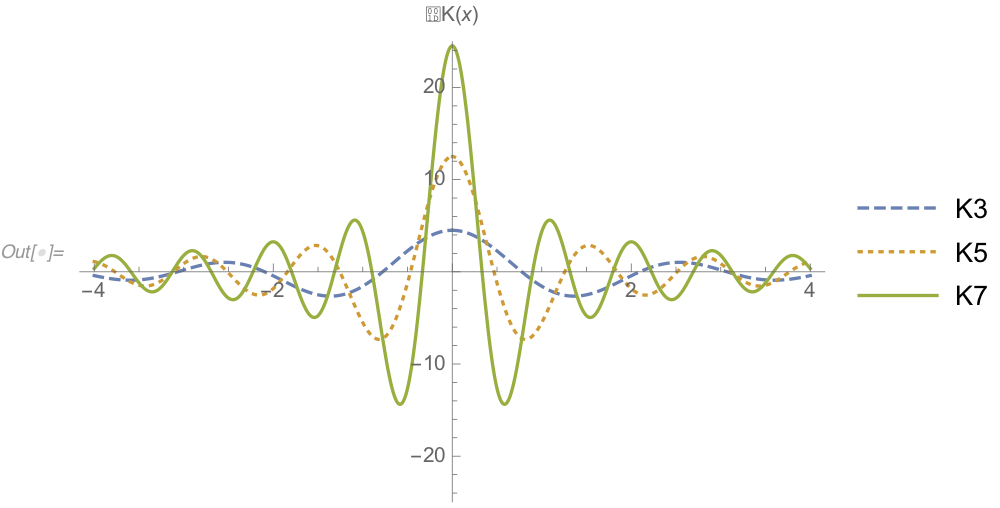
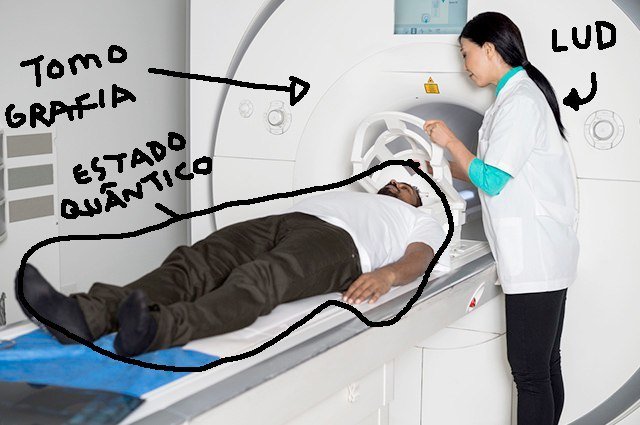
What about multi-mode state?
Convex Optmization
min
s.t
$$\rho \succeq 0$$
$$\mathrm{Tr}(\rho) = 1$$
-
Semi-definite programming
-
Fock Basis
$$\sum_{i \in \mathcal{I}} \Delta_i + \delta$$
$${\rho, \Delta, \delta}$$
$$\left\vert \mathrm{Tr}({E_i \rho) -f_i} \right\vert \leqslant \Delta_i f_i$$
$$i \in \mathcal{I}$$
$$\mathrm{Tr}({ E_i\rho} )\leqslant \delta$$
$$i \notin \mathcal{I}$$
$$\vert q_{\theta}\rangle\!\langle{q_{\theta}}\vert= \sum \psi_n^*(q) \psi_m(q) \exp[i(m-n)]\vert{n}\rangle\!\langle{m}\vert$$
Ludmila A. S. Botelho, Reinaldo O. Vianna, Eur. Phys. J. D 74, 42 (2020)
| 10.1140/epjd/e2020-100649-3 |
And now for something completely different
Separability
- Partial Transposition
$$\rho^{T_B} = \sum_i p_i \left(\rho_i^A \otimes (\rho_i^B)^T\right)$$
Huge Dimension
Separability
- Covariance Matrix
\gamma \geq \begin{pmatrix}
\gamma_A & 0 \\
0 & \gamma_B
\end{pmatrix}
- SDP
Positive Maps
- Density Operator vs Moment Matrix
- Entanglement Witness
(But Not Completely Positive)
Sep
$$\rho$$
$$\mathit{W}$$
Ent
$$M$$
$$\mathit{W}'$$
Thank You!
Tomography on Continuous Variables Quantum Systems
By ludmilaasb
