Aprendizaje profundo
Una breve introducción
Luis Manuel Román García
Contenidos
- Introducción al aprendizaje profundo
- Teoría detrás de las redes neuronales profundas
- Manos a la obra
Introducción al aprendizaje profundo
- Contexto histórico
- Poder de las redes neuronales
- Resultados notables
La evolución del aprendizaje profundo
1958
Rosenblatt desarrolla el primer modelo de aprendizaje estadístico, constituido por una función que se activa al recibir una señal de un modelo lineal en los parámetros.
Combinación lineal parámetros
Función de activación
Salida
Error
Actualización parámetros
Desafortunadamente, este algoritmo solo puede clasificar adecuadamente clases que son linealmente separables.
1960
Bernard Widrow y Tedd Hoff mejoran el perceptrón al utilizar la salida de una función lineal como criterio de decisión para actualizar los parámetros en lugar de la salida de la función escalonada. Este modelo fue conocido como ADALINE
Error
Actualización parámetros
Salida
Función de activación
Función de decisión
Combinación lineal parámetros
Gradiente
Función de costo global
Costo inicial de los parámetros
1969
Marvin Minsky y Seymour Papert dan el golpe de gracia al Perceptrón, mostrando todas las carencias del mismo en su famoso libro Perceptrons: an introduction to computational geometry
Función XOR
Uno de los primeros ejemplos que mostraban la falibilidad del perceptrón como modelo de aprendizaje fue la función XOR
(0,1) \rightarrow 1
(1,1) \rightarrow 0
(1,0) \rightarrow 1
(0,0) \rightarrow 0
Lo que queremos es un modelo que sea capaz de identificar la región amarilla.
Función XOR
1974
Se desarrolla el método a través del cual sería posible extraer los gradientes de modelos de mayor profundidad, sentando así las bases para la factibilidad del aprendizaje profundo.
Error en el nodo de salida
Gradiente en capas ocultas
Error en capas ocultas
Entrada
Predicción
Objetivo
1986
Se desarrolla el Perceptrón de múltiples capas. Se resuelven la mayor parte de los problemas de clasificación que el Perceptrón era incapaz de resolver.
Perceptrón multicapas
Surgen cuando apilamos múltiples niveles de perceptrones que se encuentran conectados entre sí y retroalimentados por funciones de activación.
O_1
O_2
O_3
\sim
\sum
\sim
\sum
\sim
\sum
\sim
\sum
\sim
\sum
\sim
\sum
\sim
\sum
X_1
X_2
X_3
¿Recuerdan este problema?
Función XOR
Función XOR
Propuesta de solución
\sim
\sum
-0.5
1
\sim
\sum
\sim
\sum
-1
+1
1
X_1
X_2
+1
+1
+1
+1
-0.5
-1.5
Función XOR
\sim
\sum
-0.5
1
\sim
\sum
\sim
\sum
-1
+1
1
X_1
X_2
+1
+1
+1
+1
-0.5
-1.5
0
1
\delta(0*1 + 1*1 + (-1.5*1))=\delta(-0.5)=0
\delta(0*1 + 1*1 + (-0.5*1))=\delta(0.5)=1
\delta(-1*0 + 1*1 + (-0.5*1))=\delta(0.5)=1
Función XOR | solución
\sim
\sum
-0.5
1
\sim
\sum
\sim
\sum
-1
+1
1
X_1
X_2
+1
+1
+1
+1
-0.5
-1.5
0
0
\delta(0*1 + 1*0 + (-1.5*1))=\delta(-1.5)=0
\delta(0*1 + 1*0 + (-0.5*1))=\delta(-0.5)=0
\delta(-1*0 + 1*0 + (-0.5*1))=\delta(-0.5)=0
Función XOR | solución
2012
El renacer de las redes neuronales profundas
Imágenes
Audio
Lenguaje
efectividad drogas | acelerador de partículas |reconstrucción cerebral | mutaciones genéticas | clasificación de temas |
análisis de sentimientos | pregunta respuesta | procesamiento de video | cómputo creativo | traducción de lenguaje
2011
Watson compite en Jeopardy! contra los campeones Brad Rutter y Ken Jennings. Watson recibe el primer premio de $1 million de dólares.
2010
2011
2012
2013
2014
2015
70%
75%
80%
85%
90%
95%
CNN
Tradicional
Precisión histórica del modelo ganador del desafío anual ImageNet
2016
Alphago es el primer algoritmo computacional capaz de derrotar al campeón del mundo en el juego de GO.
2016
El sistema ConceptNet es sometido a una prueba verbal de IQ, obtiene el "desempeño promedio de un niño de 4 años”.
Poema 1
And lying sleeping on an open bed.
And I remember having started tripping,
Or any angel hanging overhead,
Without another cup of coffee dripping.
Surrounded by a pretty little sergeant,
Another morning at an early crawl.
And from the other side of my apartment,
An empty room behind the inner wall.
Poema 2
A green nub pushes up from moist, dark soil.
Three weeks without stirring, now without strife
From the unknown depths of a thumbpot life
In patient rhythm slides forth without turmoil,
A tiny green thing poking through its sheath.
Shall I see the world? Yes, it is bright.
Silent and slow it stretches for the light
And opens, uncurling, above and beneath.
¿Cuál es el humano?
2018
Se llega a un nuevo hito en Video-to-video Synthesis, ahora es posible generar videos completamente falsos que emulen a la realidad. Esto abrió la puerta a toda una serie de modelos generativos.
2019
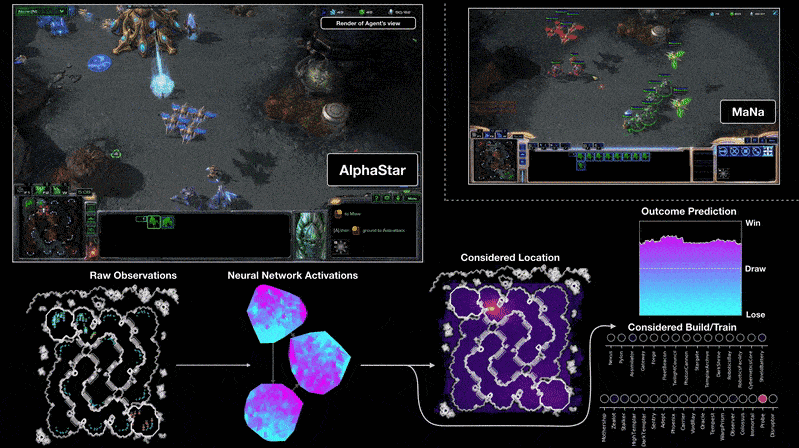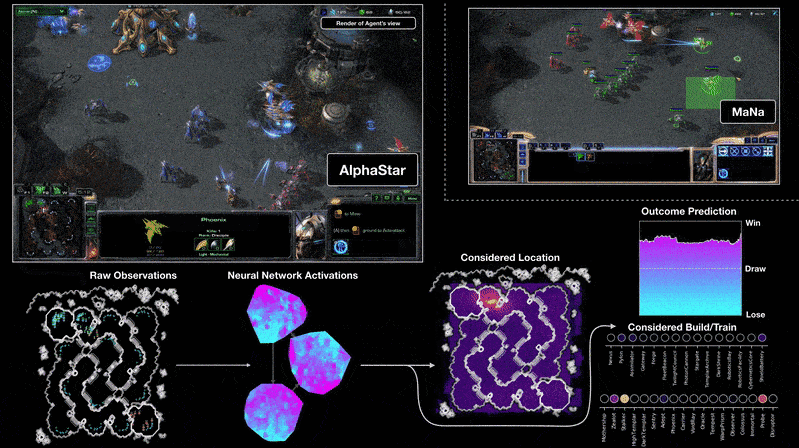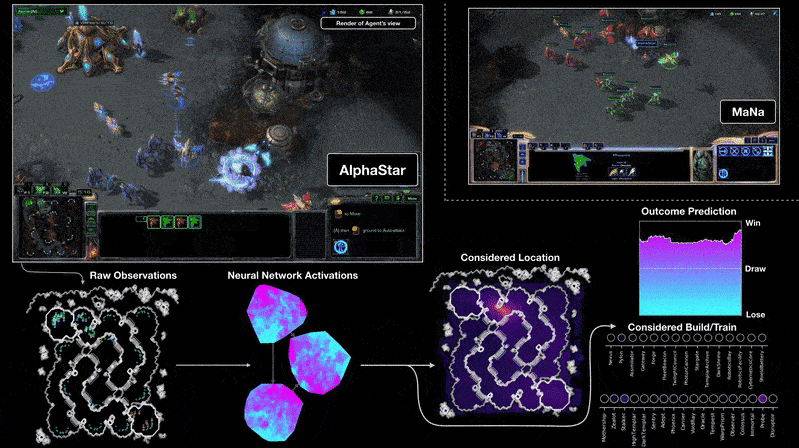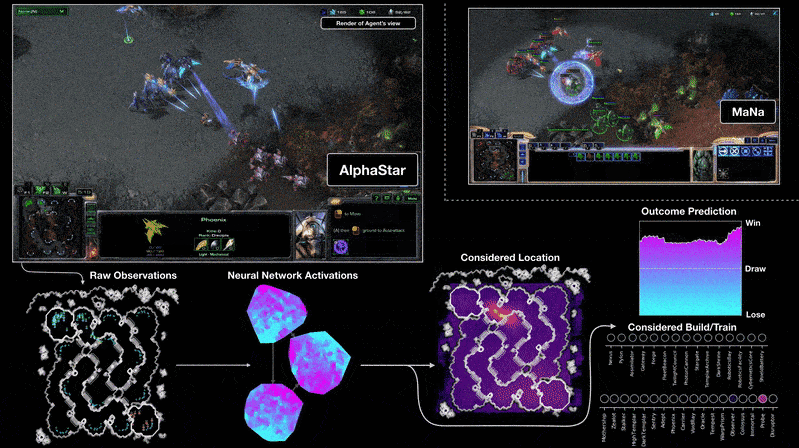
AlphaStar derrota a los mejores jugadores del mundo en StarcraftII
Teoría detrás de las redes neuronales profundas
- Definición y arquitectura
- Entrenar una red neuronal
- Diferentes arquitecturas
Hemos visto que las redes neuronales tienen propiedades interesantes. De hecho hay un par de resultados que nos aseguran que una red con dos niveles ocultos es un aproximador universal.
Redes neuronales y aprendizaje profundo
Salida ponderada RN
Salida ponderada capa oculta
Cuál es la ventaja de apilar una gran cantidad de capas en lugar de buscar la mejor combinación de parámetros en redes 'anchas'.
Redes neuronales y aprendizaje profundo
O_1
O_2
O_3
\sim
\sum
\sim
\sum
\sim
\sum
\sim
\sum
\sim
\sum
\sim
\sum
\sim
\sum
X_1
X_2
X_3
Redes neuronales y aprendizaje profundo
Eficiencia
Aprender representaciones
Las redes neuronales profundas son capaces de aprender representaciones más complejas de los parámetros sin incluir el sesgo del modelador.
Redes neuronales y aprendizaje profundo
La composición de múltiples capas hace que se puedan aprender estas representaciones de manera eficiente.
Redes neuronales y aprendizaje profundo
Sin embargo, al ser modelos tan complejos, hay que tener en consideración varios aspectos técnicos con tal de evitar utilizar estos modelos como cajas negras y caer en errores de interpretación y diseño.
Redes neuronales y aprendizaje profundo
X_1
X_2
\dots
X_n
\sim
\theta_1
\theta_2
\theta_n
X_0
\theta_0
O_i
\sum
El componente más básico de una red neuronal es la unidad de activación.
- Insumos (que pueden ser provistos por capas previas)
- El sesgo u ordenada
- Función de activación (que puede ser diferente en las capas ocultas y la de salida dependiendo el problema.
Funciones de activación
Funciones de activación
Actualmente no es muy claro qué es lo que determina que función de activación es mejor que otra para cierta aplicación.
Sin embargo, la unidad lineal rectificada tiende a ser preferida en muchas situaciones y es una buena primera opción.
Algo que vale la pena notar es que las ReLu son buenas para propagar información hacia atrás pues el modelo es lineal.
En caso de que se quieran usar activaciones sigmoidales la tangente hiperbólica tiende a ser mejor que la logística pues se satura menos en los extremos.
Funciones de activación
Funciones de activación
Funciones de activación
Epocas
Error
Propagación hacia atrás
O_1
O_2
O_3
Ahora una pregunta relevante es, cómo podemos actualizar los pesos de las capas ocultas y de la capa de entrada, cuando solo tenemos retroalimentación con respecto al error en la capa de salida.
O_1
O_2
O_3
Propagación hacia atrás
Por ejemplo, supongamos que tenemos la siguiente arquitectura.
¿Cómo podríamos actualizar ?
\alpha_{j,i}
O_1
O_2
O_3
Propagación hacia atrás
O_1
O_2
O_3
Afortunadamente, frameworks como Tensorflow y Theano nos permiten llevar a cabo diferenciación automática!
Propagación hacia atrás
Descenso por gradiente estocástico
w_{k+1} = w_k - \alpha\nabla l(h(x_i, w_k))
Cumpliendo con todos los supuestos de regularidad, lo mejor que podemos esperar es convergencia sublineal:
Mejor escenario
\mathbb{E}[F(w_k)- F(w^*)] \leq \frac{\hat{\alpha}LM}{2c\mu} + (1-\hat{\alpha})^{k-1}\Big(F(w_1)-F(w^*)-\frac{\hat{\alpha} LM}{2c\mu}\Big)
Esto se debe a que estos modelos presentan no convexidad y no linealidad en sus curvas de error.
w_{k+1} = w_k - \alpha H_{(|S|_k)} \frac{1}{|X|_k}\displaystyle\sum_{i=1}^{|X|_k}\nabla l(h_{w_k})
|S|_k\leq |X|_k
Métodos de segundo orden
Cumpliendo con todos los supuestos de regularidad, lo mejor que podemos esperar es convergencia superlineal:
Mejor escenario
|X_k| \geq |X_0|\eta_k^k;\quad |X_0|\geq\bigg(\frac{6v\gamma M}{\hat{\mu}^2}\bigg), \eta_k > \eta_{k-1}, \eta_k \rightarrow\infty, \eta_1>1
|S_k| > |S_{k-1}|;\quad \displaystyle\lim_{k\rightarrow\infty}|S_k|=\infty; \quad |S_0|\geq\bigg(\frac{4\sigma}{\hat{\mu}}\bigg)^2
\|w_0-w^*\|\leq\frac{\hat{\mu}}{3\gamma M}
\mathbb{E}[|w_k - w^*|]\leq\tau_k\quad\quad\displaystyle\lim_{k\rightarrow\infty}\frac{\tau_{k+1}}{\tau_k}\rightarrow 0
Múltiples arquitecturas
Manos a la obra
Deep Learning
By Luis Roman
