CS6015: Linear Algebra and Random Processes
Lecture 21: Principal Component Analysis (the math)
Learning Objectives
What is PCA?
What are some applications of PCA?
Recap of Wishlist
Represent the data using fewer dimensions such that
the data has high variance along these dimensions
the covariance between any two dimensions is low
the basis vectors are orthonormal
u1=[10]
\mathbf{u_1} = \begin{bmatrix}1\\0\end{bmatrix}
[x11x12]
\begin{bmatrix}x_{11}\\x_{12}\end{bmatrix}
u2=[01]
\mathbf{u_2} = \begin{bmatrix}0\\1\end{bmatrix}
v2
\mathbf{v_2}
v1
\mathbf{v_1}
We will keep the wishlist aside for now and just build some background first (mostly recap)
Projecting onto one dimension
x11x21x31……xm1x12x22x32……xm2x13x23x33……xm3x14x24x34……xm4………………x1nx2nx3n……xmn
\begin{bmatrix}
x_{11}&x_{12}&x_{13}&x_{14}& \dots &x_{1n} \\
x_{21}&x_{22}&x_{23}&x_{24}& \dots &x_{2n} \\
x_{31}&x_{32}&x_{33}&x_{34}& \dots &x_{3n} \\
\dots &\dots &\dots &\dots &\dots &\dots \\
\dots &\dots &\dots &\dots &\dots &\dots \\
x_{m1}&x_{m2}&x_{m3}&x_{m4}& \dots &x_{mn} \\
\end{bmatrix}
X1⊤
\mathbf{X_1}^\top
X2⊤
\mathbf{X_2}^\top
X3⊤
\mathbf{X_3}^\top
Xm⊤
\mathbf{X_m}^\top
X4⊤
\mathbf{X_4}^\top
X
\mathbf{X}
x1=x11u1+x12u2+⋯+x1nun
\mathbf{x_1} = x_{11}\mathbf{u_1} + x_{12}\mathbf{u_2} + \dots + x_{1n}\mathbf{u_n}
Standard Basis Vectors
(unit norms)
↑v1↓
\begin{bmatrix}
\uparrow\\
\\
v1
\\
\\
\downarrow
\end{bmatrix}
New Basis Vector
(unit norm)
x1=x11^v1
\mathbf{x_1} = \hat{x_{11}}\mathbf{v1}
x11^=v1⊤v1x1⊤v1=x1⊤v1
\hat{x_{11}} = \frac{\mathbf{x_1}^\top \mathbf{v1}}{\mathbf{v1}^\top \mathbf{v1}} = \mathbf{x_1}^\top \mathbf{v1}
x2=x21^v1
\mathbf{x_2} = \hat{x_{21}}\mathbf{v1}
x21^=v1⊤v1x2⊤v1=x2⊤v1
\hat{x_{21}} = \frac{\mathbf{x_2}^\top \mathbf{v1}}{\mathbf{v1}^\top \mathbf{v1}} = \mathbf{x_2}^\top \mathbf{v1}
u2=[01]
\mathbf{u2} = \begin{bmatrix} 0\\1 \end{bmatrix}
u1=[10]
\mathbf{u1} = \begin{bmatrix} 1\\0 \end{bmatrix}
[x11x12]
\begin {bmatrix}
x_{11}\\
x_{12}
\end {bmatrix}
Projecting onto two dimensions
x11x21x31……xm1x12x22x32……xm2x13x23x33……xm3x14x24x34……xm4………………x1nx2nx3n……xmn
\begin{bmatrix}
x_{11}&x_{12}&x_{13}&x_{14}& \dots &x_{1n} \\
x_{21}&x_{22}&x_{23}&x_{24}& \dots &x_{2n} \\
x_{31}&x_{32}&x_{33}&x_{34}& \dots &x_{3n} \\
\dots &\dots &\dots &\dots &\dots &\dots \\
\dots &\dots &\dots &\dots &\dots &\dots \\
x_{m1}&x_{m2}&x_{m3}&x_{m4}& \dots &x_{mn} \\
\end{bmatrix}
X1⊤
\mathbf{X_1}^\top
X2⊤
\mathbf{X_2}^\top
X3⊤
\mathbf{X_3}^\top
Xm⊤
\mathbf{X_m}^\top
X4⊤
\mathbf{X_4}^\top
X
\mathbf{X}
↑v1↓↑v2↓
\begin{bmatrix}
\uparrow & \uparrow
\\
\\
\mathbf{\scriptsize v_1} & \mathbf{\scriptsize v_2}
\\
\\
\downarrow & \downarrow
\end{bmatrix}
new basis vectors
(unit norm)
x1=x11^v1+x12^v2
\mathbf{x_1} = \hat{x_{11}}\mathbf{v_1}+\hat{x_{12}}\mathbf{v_2}
x11^=x1⊤v1
\hat{x_{11}} = \mathbf{x_1}^\top \mathbf{v_1}
x2=x21^v1+x22^v2
\mathbf{x_2} = \hat{x_{21}}\mathbf{v_1}+\hat{x_{22}}\mathbf{v_2}
x21^=x2⊤v1
\hat{x_{21}} = \mathbf{x_2}^\top \mathbf{v_1}
u2=[01]
\mathbf{u_2} = \begin{bmatrix} 0\\1 \end{bmatrix}
u1=[10]
\mathbf{u_1} = \begin{bmatrix} 1\\0 \end{bmatrix}
[x11x12]
\begin {bmatrix}
x_{11}\\
x_{12}
\end {bmatrix}
X^=
\mathbf{\hat{\textit{X}}} =
x11^x21^x31^……xm1^x12^x22^x32^……xm2^
\begin{bmatrix}
\hat{x_{11}}&\hat{x_{12}}\\
\hat{x_{21}}&\hat{x_{22}}\\
\hat{x_{31}}&\hat{x_{32}}\\
\dots &\dots\\
\dots &\dots\\
\hat{x_{m1}}&\hat{x_{m2}}\\
\end{bmatrix}
=
\mathbf{=}
x1⊤v1x2⊤v1x3⊤v1……xm⊤v1x1⊤v2x2⊤v2x3⊤v2……xm⊤v2
\begin{bmatrix}
\mathbf{x_{1}}^\top \mathbf{v_{1}}&\mathbf{x_{1}}^\top \mathbf{v_{2}} \\
\mathbf{x_{2}}^\top \mathbf{v_{1}}&\mathbf{x_{2}}^\top \mathbf{v_{2}} \\
\mathbf{x_{3}}^\top \mathbf{v_{1}}&\mathbf{x_{3}}^\top \mathbf{v_{2}} \\
\dots &\dots \\
\dots &\dots \\
\mathbf{x_{m}}^\top \mathbf{v_{1}}&\mathbf{x_{m}}^\top \mathbf{v_{2}} \\
\end{bmatrix}
=XV
\mathbf{= \textit{XV}}
x12^=x1⊤v2
\hat{x_{12}} = \mathbf{x_1}^\top \mathbf{v_2}
x21^=x2⊤v2
\hat{x_{21}} = \mathbf{x_2}^\top \mathbf{v_2}
v1
\mathbf{v_1}
V
\mathbf{\textit{V}}
v2
\mathbf{v_2}
Projecting onto k dimension
x11^x21^x31^……xm1^x12^x22^x32^……xm2^………………x1k^x2k^x3k^……xmk^
\begin{bmatrix}
\hat{x_{11}}&\hat{x_{12}}& \dots &\hat{x_{1k}} \\
\hat{x_{21}}&\hat{x_{22}}& \dots &\hat{x_{2k}} \\
\hat{x_{31}}&\hat{x_{32}}& \dots &\hat{x_{3k}} \\
\dots &\dots &\dots &\dots \\
\dots &\dots &\dots &\dots \\
\hat{x_{m1}}&\hat{x_{m2}}& \dots &\hat{x_{mk}} \\
\end{bmatrix}
X1⊤
\mathbf{X_1}^\top
X2⊤
\mathbf{X_2}^\top
X3⊤
\mathbf{X_3}^\top
Xm⊤
\mathbf{X_m}^\top
X4⊤
\mathbf{X_4}^\top
X
\mathbf{\textit{X}}
↑v1↓↑v2↓⋯⋯⋯↑vk↓
\begin{bmatrix}
\uparrow & \uparrow & \cdots & \uparrow
\\
\\
\mathbf{\scriptsize v1} & \mathbf{\scriptsize v2} & \cdots & \mathbf{\scriptsize vk}
\\
\\
\downarrow & \downarrow & \cdots & \downarrow
\end{bmatrix}
New Basis Vectors
(unit norm)
x11x21x31……xm1x12x22x32……xm2x13x23x33……xm3x14x24x34……xm4………………x1nx2nx3n……xmn
\begin{bmatrix}
x_{11}&x_{12}&x_{13}&x_{14}& \dots &x_{1n} \\
x_{21}&x_{22}&x_{23}&x_{24}& \dots &x_{2n} \\
x_{31}&x_{32}&x_{33}&x_{34}& \dots &x_{3n} \\
\dots &\dots &\dots &\dots &\dots &\dots \\
\dots &\dots &\dots &\dots &\dots &\dots \\
x_{m1}&x_{m2}&x_{m3}&x_{m4}& \dots &x_{mn} \\
\end{bmatrix}
X^=
\mathbf{\hat{\textit{X}}} =
V
\mathbf{\textit{V}}
x1⊤v1x2⊤v1x3⊤v1……xm⊤v1x1⊤v2x2⊤v2x3⊤v2……xm⊤v2………………x1⊤vkx2⊤vkx3⊤vk……xm⊤vk
\begin{bmatrix}
\mathbf{x_{1}}^\top \mathbf{v_{1}}&\mathbf{x_{1}}^\top \mathbf{v_{2}}&\dots&\mathbf{x_{1}}^\top \mathbf{v_{k}} \\
\mathbf{x_{2}}^\top \mathbf{v_{1}}&\mathbf{x_{2}}^\top \mathbf{v_{2}}&\dots&\mathbf{x_{2}}^\top \mathbf{v_{k}}\\
\mathbf{x_{3}}^\top \mathbf{v_{1}}&\mathbf{x_{3}}^\top \mathbf{v_{2}}&\dots&\mathbf{x_{3}}^\top \mathbf{v_{k}} \\
\dots &\dots &\dots &\dots \\
\dots &\dots &\dots &\dots \\
\mathbf{x_{m}}^\top \mathbf{v_{1}}&\mathbf{x_{m}}^\top \mathbf{v_{2}}&\dots&\mathbf{x_{m}}^\top \mathbf{v_{k}} \\
\end{bmatrix}
=XV
\mathbf{= \textit{XV}}
=
\mathbf{=}
We want to find a V such that
columns of V are ortho-normal
columns of X^ have high variance
What is the new covariance matrix?
X^=XV
\hat{X} = XV
Σ^=m1X^TX^
\hat{\Sigma} = \frac{1}{m}\hat{X}^T\hat{X}
Σ^=m1(XV)T(XV)
\hat{\Sigma} = \frac{1}{m}(XV)^T(XV)
Σ^=VT(m1XTX)V
\hat{\Sigma} = V^T(\frac{1}{m}X^TX)V
What do we want?
Σ^ij=Cov(i,j)
\hat{\Sigma}_{ij} = Cov(i,j)
if i=j
\text{ if } i \neq j
low covariance
=0
= 0
=σi2
= \sigma^2_i
if i=j
\text{ if } i = j
=0
\neq 0
high variance
We want Σ^ to be diagonal
We are looking for orthogonal vectors which will diagonalise m1XTX :-)
These would be eigenvectors of XTX
(Note that the eigenvectors of cA are the same as the eigenvectors of A)
The eigenbasis of XTX
Σ^=VT(m1XTX)V=D
\hat{\Sigma} = V^T(\frac{1}{m}X^TX)V = D
We have found a V such that
columns of V are orthonormal
eigenvectors of a symmetric matrix
columns of X^ have zero covariance
diagonal
The right basis to use is the eigenbasis of XTX
What about the variance of the columns of X^ ?
?
?
✓
\checkmark
✓
\checkmark
What is the variance of the cols of X^ ?
The i-th column of X^ is
The variance for the i-th column is
The i-th column of X^ is
σi2 = m1X^iTX^i
X
\mathbf{\textit{X}}
↑v1↓↑v2↓⋯⋯⋯↑vk↓
\begin{bmatrix}
\uparrow & \uparrow & \cdots & \uparrow
\\
\\
\mathbf{\scriptsize v1} & \mathbf{\scriptsize v2} & \cdots & \mathbf{\scriptsize vk}
\\
\\
\downarrow & \downarrow & \cdots & \downarrow
\end{bmatrix}
x11x21x31……xm1x12x22x32……xm2x13x23x33……xm3x14x24x34……xm4………………x1nx2nx3n……xmn
\begin{bmatrix}
x_{11}&x_{12}&x_{13}&x_{14}& \dots &x_{1n} \\
x_{21}&x_{22}&x_{23}&x_{24}& \dots &x_{2n} \\
x_{31}&x_{32}&x_{33}&x_{34}& \dots &x_{3n} \\
\dots &\dots &\dots &\dots &\dots &\dots \\
\dots &\dots &\dots &\dots &\dots &\dots \\
x_{m1}&x_{m2}&x_{m3}&x_{m4}& \dots &x_{mn} \\
\end{bmatrix}
V
\mathbf{\textit{V}}
x1⊤v1x2⊤v1x3⊤v1……xm⊤v1x1⊤v2x2⊤v2x3⊤v2……xm⊤v2………………x1⊤vkx2⊤vkx3⊤vk……xm⊤vk
\begin{bmatrix}
\mathbf{x_{1}}^\top \mathbf{v_{1}}&\mathbf{x_{1}}^\top \mathbf{v_{2}}&\dots&\mathbf{x_{1}}^\top \mathbf{v_{k}} \\
\mathbf{x_{2}}^\top \mathbf{v_{1}}&\mathbf{x_{2}}^\top \mathbf{v_{2}}&\dots&\mathbf{x_{2}}^\top \mathbf{v_{k}}\\
\mathbf{x_{3}}^\top \mathbf{v_{1}}&\mathbf{x_{3}}^\top \mathbf{v_{2}}&\dots&\mathbf{x_{3}}^\top \mathbf{v_{k}} \\
\dots &\dots &\dots &\dots \\
\dots &\dots &\dots &\dots \\
\mathbf{x_{m}}^\top \mathbf{v_{1}}&\mathbf{x_{m}}^\top \mathbf{v_{2}}&\dots&\mathbf{x_{m}}^\top \mathbf{v_{k}} \\
\end{bmatrix}
The variance for the i-th column is
X^i = Xvi
X^=
\mathbf{\hat{X} =}
X^1
\mathbf{\hat{X}_{1} }
X^2
\mathbf{\hat{X}_{2} }
X^n
\mathbf{\hat{X}_{n} }
The i-th column of X^ is
The variance for the i-th column is
X^i = Xvi
σi2 = m1X^iTX^i
= m1(Xvi)TXvi
= m1viTXTXvi
= m1viTλivi
= m1(Xvi)TXvi
= m1viTXTXvi
= m1viTλivi
= m1λi
= m1λi
(∵viTvi=1)
The full story
(How would you do this in practice?)
Compute the n eigen vectors of X TX
Sort them according to the corresponding eigenvalues
Retain only those eigenvectors corresponding to the top-k eigenvalues
Project the data onto these k eigenvectors
We know that n such vectors will exist since it is a symmetric matrix
These are called the principal components
Heuristics: k=50,100 or choose k such that λk/λmax > t
Reconstruction Error
x=[x11x12]=[3.33]
\mathbf{x} =
\begin{bmatrix}x_{11}\\x_{12}\end{bmatrix} =
\begin{bmatrix}3.3\\3\end{bmatrix}
Suppose
x=3.3u1+3u2
\mathbf{x} = {3.3u_{1} + 3u_{2}}
Let
v1=[11]v2=[−11]
\mathbf{v_{1}} = \begin{bmatrix}1\\1\end{bmatrix}
\mathbf{v_{2}} = \begin{bmatrix}-1\\1\end{bmatrix}
v1=2121v2=−2121
\mathbf{v_{1}} = \begin{bmatrix}\frac{\mathbf{1}}{\sqrt{2}} \\ \\ \frac{\mathbf{1}}{\sqrt{2}}\end{bmatrix}
\mathbf{v_{2}} = \begin{bmatrix}-\frac{\mathbf{1}}{\sqrt{2}} \\ \\ \frac{\mathbf{1}}{\sqrt{2}}\end{bmatrix}
x=b11v1+b12v2b11=x⊤v1=26.3b12=x⊤v2=−20.326.3v1+2−0.3v2=[3.33]=x
\mathbf{x} = b_{11}\mathbf{v_{1}} + b_{12}\mathbf{v_{2}} \\
b_{11} = \mathbf{x^{\top}v_{1}} = \frac{6.3}{\sqrt{2}} \\
b_{12} = \mathbf{x^{\top}v_{2}} = -\frac{0.3}{\sqrt{2}} \\
\frac{6.3}{\sqrt{2}} \mathbf{v_{1}} + \frac{-0.3}{\sqrt{2}}\mathbf{v_{2}} =\begin{bmatrix}3.3\\3\end{bmatrix} =\mathbf{x}
u2=[01]
\mathbf{u_2} = \begin{bmatrix}0\\1\end{bmatrix}
u1=[10]
\mathbf{u_1} = \begin{bmatrix}1\\0\end{bmatrix}
[3.33]
\begin{bmatrix}3.3\\3\end{bmatrix}
if we use all the n eigenvectors
we will get an exact reconstruction of the data
one data point
new basis vectors
unit norm
Reconstruction Error
x=[x11x12]=[3.33]
\mathbf{x} =
\begin{bmatrix}x_{11}\\x_{12}\end{bmatrix} =
\begin{bmatrix}3.3\\3\end{bmatrix}
Suppose
x=3.3u1+3u2
\mathbf{x} = {3.3u_{1} + 3u_{2}}
Let
v1=[11]v2=[−11]
\mathbf{v_{1}} = \begin{bmatrix}1\\1\end{bmatrix}
\mathbf{v_{2}} = \begin{bmatrix}-1\\1\end{bmatrix}
v1=2121v2=−2121
\mathbf{v_{1}} = \begin{bmatrix}\frac{\mathbf{1}}{\sqrt{2}} \\ \\ \frac{\mathbf{1}}{\sqrt{2}}\end{bmatrix}
\mathbf{v_{2}} = \begin{bmatrix}-\frac{\mathbf{1}}{\sqrt{2}} \\ \\ \frac{\mathbf{1}}{\sqrt{2}}\end{bmatrix}
x=b11v1+b12v2b11=x⊤v1=26.326.3v1=[3.153.15]=x
\mathbf{x} = b_{11}\mathbf{v_{1}} + b_{12}\mathbf{v_{2}} \\
b_{11} = \mathbf{x^{\top}v_{1}} = \frac{6.3}{\sqrt{2}} \\ \\ \\
\newline
\newline
\frac{6.3}{\sqrt{2}} \mathbf{v_{1}} =\begin{bmatrix}3.15\\3.15\end{bmatrix} =\mathbf{x}
u2=[01]
\mathbf{u_2} = \begin{bmatrix}0\\1\end{bmatrix}
u1=[10]
\mathbf{u_1} = \begin{bmatrix}1\\0\end{bmatrix}
[3.33]
\begin{bmatrix}3.3\\3\end{bmatrix}
but we are going
to use fewer
eigenvectors
(we will throw away v2)
one data point
new basis vectors
unit norm
Reconstruction Error
x=[3.33]x^=[3.153.15]
\mathbf{x} =
\begin{bmatrix}3.3\\3\end{bmatrix}
\mathbf{\hat{x}} =
\begin{bmatrix}3.15\\3.15\end{bmatrix}
u2=[01]
\mathbf{u_2} = \begin{bmatrix}0\\1\end{bmatrix}
u1=[10]
\mathbf{u_1} = \begin{bmatrix}1\\0\end{bmatrix}
[3.33]
\begin{bmatrix}3.3\\3\end{bmatrix}
original x
x−x^(x−x^)⊤(x−x^)
\mathbf{x-\hat{x}} \\
(\mathbf{x-\hat{x}})^{\top} (\mathbf{x-\hat{x}})
min∑i=im(x−x^)⊤(x−x^)
min\sum_{i=i}^{m} (\mathbf{x-\hat{x}})^{\top} (\mathbf{x-\hat{x}})
xi=∑j=1nbijvj
\mathbf{x_{i}} = \sum_{j=1}^{n} b_{ij}\mathbf{v_{j}} \\
x reconstructed from
fewer eigen vectors
reconstruction error vector
reconstruction error vector
(length of the error)
xi^=∑j=1kbijvj
\mathbf{\hat{x_{i}}} = \sum_{j=1}^{k} b_{ij}\mathbf{v_{j}}
original x - reconstructed from all n eigenvectors
reconstructed only from top K eigenvectors
solving the above optimization problem corresponds to choosing the eigen basis while discarding the eigenvectors corresponding to the smallest eigen values
Recap
[v]S
[\mathbf{v}]_S
S−1
S^{-1}
[Akv0]S
[A^k\mathbf{v}_0]_S
Λk
\Lambda^k
O(n2)
O(n^2)
Akv=SΛkS−1v
A^{k}\mathbf{v} = S\Lambda^{k}S^{-1}\mathbf{v}
S
S
O(n2)
O(n^2)
O(nk)
O(nk)
O(kn3)
O(kn^3)
O(n2+nk+n2)
O(n^2 + nk + n^2)
+ the cost of computing EVs
EVD/Diagonalization/Eigenbasis is useful when the same matrix A operates on many vectors repeatedly (i.e., if we want to apply An to many vectors)
(this one time cost is then justified in the long run)
v
\mathbf{v}
Akv
A^k\mathbf{v}
Ak
A^k
O(kn3)
O(kn^3)
(diagonalisation leads to computational efficiency)
Recap
[v]S
[\mathbf{v}]_S
S−1
S^{-1}
[Akv0]S
[A^k\mathbf{v}_0]_S
Λk
\Lambda^k
O(n2)
O(n^2)
Akv=SΛkS−1v
A^{k}\mathbf{v} = S\Lambda^{k}S^{-1}\mathbf{v}
S
S
O(n2)
O(n^2)
O(nk)
O(nk)
O(kn3)
O(kn^3)
O(n2+nk+n2)
O(n^2 + nk + n^2)
v
\mathbf{v}
Akv
A^k\mathbf{v}
Ak
A^k
O(kn3)
O(kn^3)
(diagonalisation leads to computational efficiency)
But this is only for square matrices!
What about rectangular matrices?
Even better for symmetric matrices
A=QΛQ⊤
A = Q\Lambda Q^\top
(orthonormal basis)
Wishlist
Can we diagonalise rectangular matrices?
m×nAn×1x=m×mU m×nΣ n×nV⊤n×1x
\underbrace{A}_{m\times n}\underbrace{\mathbf{x}}_{n \times 1} = \underbrace{U}_{m\times m}~\underbrace{\Sigma}_{m\times n}~\underbrace{V^\top}_{n\times n}\underbrace{\mathbf{x}}_{n \times 1}
Translating from std. basis to this new basis
The transformation becomes very simple in this basis
Translate back to the standard basis
(all off-diagonal elements are 0)
(orthonormal)
(orthonormal)
Recap: square matrices
A=SΛS−1
A = S\Lambda S^{-1}
A=QΛQ⊤
A = Q\Lambda Q^\top
(symmetric)
Yes, we can!
(true for all matrices)
The 4 fundamental subspaces: basis
Let Am×n be a rank r matrix
u1,u2,…,ur be an orthonormal basis for C(A)
ur+1,ur+2,…,um be an orthonormal basis for N(A⊤)
v1,v2,…,vr be an orthonormal basis for C(A⊤)
vr+1,vr+2,…,vn be an orthonormal basis for N(A)
Let Am×n be a rank r matrix
Fact 1: Such basis always exist
Fact 2: u1,u2,…,ur,ur+1,…,um are orthonormal
In addition, we want
v1,v2,…,vr,vr+1,…,vn are orthonormal
Avi=σiui ∀i≤r
A\mathbf{v_i} = \sigma_i\mathbf{u_i}~~\forall i\leq r
∴A↑v1↓↑…↓↑vr↓=↑u1↓↑…↓↑ur↓σ100………00σr
\therefore A
\begin{bmatrix}
\uparrow&\uparrow&\uparrow \\
\mathbf{v}_1&\dots&\mathbf{v}_r \\
\downarrow&\downarrow&\downarrow \\
\end{bmatrix}
=
\begin{bmatrix}
\uparrow&\uparrow&\uparrow \\
\mathbf{u}_1&\dots&\mathbf{u}_r \\
\downarrow&\downarrow&\downarrow \\
\end{bmatrix}
\begin{bmatrix}
\sigma_1&\dots&0 \\
0&\dots&0 \\
0&\dots&\sigma_r \\
\end{bmatrix}
The 4 fundamental subspaces: basis
A↑v1↓↑…↓↑vr↓=↑u1↓↑…↓↑ur↓σ100………00σr
A
\begin{bmatrix}
\uparrow&\uparrow&\uparrow \\
\mathbf{v}_1&\dots&\mathbf{v}_r \\
\downarrow&\downarrow&\downarrow \\
\end{bmatrix}
=
\begin{bmatrix}
\uparrow&\uparrow&\uparrow \\
\mathbf{u}_1&\dots&\mathbf{u}_r \\
\downarrow&\downarrow&\downarrow \\
\end{bmatrix}
\begin{bmatrix}
\sigma_1&\dots&0 \\
0&\dots&0 \\
0&\dots&\sigma_r \\
\end{bmatrix}
Finding U and V
m×nA n×rVr=m×rUr r×rΣ
\underbrace{A}_{m\times n}~\underbrace{V_r}_{n \times r} = \underbrace{U_r}_{m \times r}~\underbrace{\Sigma}_{r \times r}
(we don't know what such V and U are - we are just hoping that they exist)
∴A↑v1↓↑…↓↑vr↓↑vr+1↓↑…↓vn=↑u1↓↑…↓↑ur↓↑ur+1↓↑…↓↑um↓σ10000……………00σr000000000000
\therefore A
\begin{bmatrix}
\uparrow&\uparrow&\uparrow&\uparrow&\uparrow \\
\mathbf{v}_1&\dots&\mathbf{v}_{r}&\mathbf{v}_{r+1}&\dots&\mathbf{v}_n \\
\downarrow&\downarrow&\downarrow&\downarrow&\downarrow \\
\end{bmatrix}=
\begin{bmatrix}
\uparrow&\uparrow&\uparrow&\uparrow&\uparrow&\uparrow \\
\mathbf{u}_1&\dots&\mathbf{u}_r&\mathbf{u}_{r+1}&\dots&\mathbf{u}_m \\
\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow \\
\end{bmatrix}
\begin{bmatrix}
\sigma_1&\dots&0&0&0 \\
0&\dots&0&0&0 \\
0&\dots&\sigma_r&0&0 \\
0&\dots&0&0&0 \\
0&\dots&0&0&0 \\
\end{bmatrix}
If Vr and Ur exist then
null space
First r columns of this product will be and the last n-r columns will be 0
n-r 0 colums
m-r 0 rows
m×nA n×nV=m×mU m×nΣ
\underbrace{A}_{m\times n}~\underbrace{V}_{n \times n} = \underbrace{U}_{m \times m}~\underbrace{\Sigma}_{m \times n}
V and U also exist
The last m-r columns of U will not contribute and hence the first r columns will be the same as and the last n-r columns will be 0
UrΣ
U_r \Sigma
AVr
AV_r
Finding U and V
AV=UΣ
AV=U\Sigma
A=UΣV⊤
A=U\Sigma V^\top
A⊤A=(UΣV⊤)⊤UΣV⊤
A^\top A=(U\Sigma V^\top)^\top U\Sigma V^\top
A⊤A=VΣ⊤U⊤UΣV⊤
A^\top A=V\Sigma^\top U^\top U\Sigma V^\top
A⊤A=VΣ⊤ΣV⊤
A^\top A=V\Sigma^\top\Sigma V^\top
diagonal
orthogonal
orthogonal
V is thus the matrix of the n eigen vectors of A⊤A
we know that this always exists because A'A is a symmetric matrix
AV=UΣ
AV=U\Sigma
A=UΣV⊤
A=U\Sigma V^\top
AA⊤=UΣV⊤(UΣV⊤)⊤
AA^\top =U\Sigma V^\top(U\Sigma V^\top)^\top
AA⊤=UΣV⊤VΣ⊤U⊤
AA^\top =U\Sigma V^\top V\Sigma^\top U^\top
AA⊤=UΣΣ⊤U⊤
AA^\top=U\Sigma\Sigma^\top U^\top
diagonal
orthogonal
orthogonal
U is thus the matrix of the m eigen vectors of AA⊤
we know that this always exists because AA' is a symmetric matrix
Σ⊤Σ contains the eigenvalues of A⊤A
HW5:Prove that the non-0 eigenvalues of AA' and A'A are always equal
Finding U and V
m×nA=m×mU m×nΣ n×nV⊤
\underbrace{A}_{m\times n} = \underbrace{U}_{m\times m}~\underbrace{\Sigma}_{m\times n}~\underbrace{V^\top}_{n\times n}
eigenvectors of AA'
transpose of the eigenvectors of A'A
square root of the eigenvalues of A'A or AA'
This is called the Singular Value Decomposition of A
∵U and V always exist, the SVD of any matrix A is always possible
since they are eigenvectors of a symmetric matrix
Some questions
∴A↑v1↓↑…↓↑vr↓↑vr+1↓↑…↓vn=↑u1↓↑…↓↑ur↓↑ur+1↓↑…↓↑um↓σ10000……………00σr000000000000
\therefore A
\begin{bmatrix}
\uparrow&\uparrow&\uparrow&\uparrow&\uparrow \\
\mathbf{v}_1&\dots&\mathbf{v}_{r}&\mathbf{v}_{r+1}&\dots&\mathbf{v}_n \\
\downarrow&\downarrow&\downarrow&\downarrow&\downarrow \\
\end{bmatrix}=
\begin{bmatrix}
\uparrow&\uparrow&\uparrow&\uparrow&\uparrow&\uparrow \\
\mathbf{u}_1&\dots&\mathbf{u}_r&\mathbf{u}_{r+1}&\dots&\mathbf{u}_m \\
\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow \\
\end{bmatrix}
\begin{bmatrix}
\sigma_1&\dots&0&0&0 \\
0&\dots&0&0&0 \\
0&\dots&\sigma_r&0&0 \\
0&\dots&0&0&0 \\
0&\dots&0&0&0 \\
\end{bmatrix}
How do we know for sure that these σs will be 0?
Recall: rank(A)=rank(A⊤A)=r
If rank(A)<n then rank A⊤A<n⟹A⊤A is singular
⟹A⊤A has 0 eigenvalues
How many?
as many as the dimension of the nullspace: n−r
Some questions
∴A↑v1↓↑…↓↑vr↓↑vr+1↓↑…↓vn=↑u1↓↑…↓↑ur↓↑ur+1↓↑…↓↑um↓σ10000……………00σr000000000000
\therefore A
\begin{bmatrix}
\uparrow&\uparrow&\uparrow&\uparrow&\uparrow \\
\mathbf{v}_1&\dots&\mathbf{v}_{r}&\mathbf{v}_{r+1}&\dots&\mathbf{v}_n \\
\downarrow&\downarrow&\downarrow&\downarrow&\downarrow \\
\end{bmatrix}=
\begin{bmatrix}
\uparrow&\uparrow&\uparrow&\uparrow&\uparrow&\uparrow \\
\mathbf{u}_1&\dots&\mathbf{u}_r&\mathbf{u}_{r+1}&\dots&\mathbf{u}_m \\
\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow \\
\end{bmatrix}
\begin{bmatrix}
\sigma_1&\dots&0&0&0 \\
0&\dots&0&0&0 \\
0&\dots&\sigma_r&0&0 \\
0&\dots&0&0&0 \\
0&\dots&0&0&0 \\
\end{bmatrix}
How do we know that these form a basis for the column space of A?
How do we know that these form a basis for the rowspace of A?
\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}
\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}
so far we only know that these are the eigenvectors of AA'
so far we only know that these are the eigenvectors of A'A
Please work this out! You really need to see this on your own! HW5
Why do we care about SVD?
A=UΣV⊤
A=U\Sigma V^\top
∴A=↑u1↓↑…↓↑ur↓↑…↓↑um↓σ10000……………00σr00000000000000000←←←………v1⊤vr⊤vn⊤⋯⋯⋯………→→→
\therefore A=
\begin{bmatrix}
\uparrow&\uparrow&\uparrow&\uparrow&\uparrow \\
\mathbf{u}_1&\dots&\mathbf{u}_r&\dots&\mathbf{u}_m \\
&\\
&\\
\downarrow&\downarrow&\downarrow&\downarrow&\downarrow\\
\end{bmatrix}
\begin{bmatrix}
\sigma_1&\dots&0&0&0&0 \\
0&\dots&0&0&0&0 \\
0&\dots&\sigma_r&0&0&0 \\
0&\dots&0&0&0&0 \\
0&\dots&0&0&0&0 \\
\end{bmatrix}
\begin{bmatrix}
\leftarrow&\dots&\mathbf{v}_{1}^\top&\cdots&\dots&\rightarrow \\
&\\
\leftarrow&\dots&\mathbf{v}_{r}^\top&\cdots&\dots&\rightarrow \\
&\\
&\\
\leftarrow&\dots&\mathbf{v}_{n}^\top&\cdots&\dots&\rightarrow \\
\end{bmatrix}
∴A=↑σ1u1↓↑…↓↑σrur↓↑…↓↑0↓←←←………v1⊤vr⊤vn⊤⋯⋯⋯………→→→
\therefore A=
\begin{bmatrix}
\uparrow&\uparrow&\uparrow&\uparrow&\uparrow \\
\sigma_1\mathbf{u}_1&\dots&\sigma_r\mathbf{u}_r&\dots&0 \\
&\\
&\\
\downarrow&\downarrow&\downarrow&\downarrow&\downarrow\\
\end{bmatrix}
\begin{bmatrix}
\leftarrow&\dots&\mathbf{v}_{1}^\top&\cdots&\dots&\rightarrow \\
&\\
\leftarrow&\dots&\mathbf{v}_{r}^\top&\cdots&\dots&\rightarrow \\
&\\
&\\
\leftarrow&\dots&\mathbf{v}_{n}^\top&\cdots&\dots&\rightarrow \\
\end{bmatrix}
∴A=σ1u1v1⊤+σ2u2v2⊤+⋯+σrurvr⊤
\therefore A=\sigma_1\mathbf{u_1}\mathbf{v_1}^\top+\sigma_2\mathbf{u_2}\mathbf{v_2}^\top+\cdots+\sigma_r\mathbf{u_r}\mathbf{v_r}^\top
n-r 0 columns
Why do we care about SVD?
A=UΣV⊤
A=U\Sigma V^\top
∴A=σ1u1v1⊤+σ2u2v2⊤+⋯+σrurvr⊤
\therefore A=\sigma_1\mathbf{u_1}\mathbf{v_1}^\top+\sigma_2\mathbf{u_2}\mathbf{v_2}^\top+\cdots+\sigma_r\mathbf{u_r}\mathbf{v_r}^\top
largest sigma
smallest sigma
we can sort these terms according to sigmas
A has m ×n elements
Each ui has m elements
Each vi has n elements
After SVD you can represent A using r(m+n+1) elements
If the rank is very small then this would lead to significant compression
Even further compression can be obtained by throwing away terms corresponding to vert small σs
Fun with flags :-)
Original Image: 1200 x 800
Lot of redundancy
rank<<800
Original Image: 1200 x 800
Lot of redundancy
rank<<800
Puzzle: What is the rank of this flag?
Best rank-k approximation
∣∣A∣∣F=∑i=1m∑j=1n∣Aij∣2
||A||_F = \sqrt{\sum_{i=1}^m\sum_{j=1}^n |A_{ij}|^2}
A=σ1u1v1⊤+σ2u2v2⊤+⋯+σkukvk⊤+⋯+σrurvr⊤
A=\sigma_1\mathbf{u_1}\mathbf{v_1}^\top+\sigma_2\mathbf{u_2}\mathbf{v_2}^\top+\cdots+\sigma_k\mathbf{u_k}\mathbf{v_k}^\top+\cdots+\sigma_r\mathbf{u_r}\mathbf{v_r}^\top
Frobenius norm
A^k=σ1u1v1⊤+σ2u2v2⊤+⋯+σkukvk⊤
\hat{A}_k=\sigma_1\mathbf{u_1}\mathbf{v_1}^\top+\sigma_2\mathbf{u_2}\mathbf{v_2}^\top+\cdots+\sigma_k\mathbf{u_k}\mathbf{v_k}^\top
rank-k approximation of A - dropped the last r - k terms
Theorem: SVD gives the best rank-k approximation of the matrix A
i.e. ∣∣A−A^k∣∣F is minimum when
A^k=UkΣkVkT
\hat{A}_k=U_k\Sigma_kV^T_k
we will not prove this
Summary of the course
(in 3 pictures)
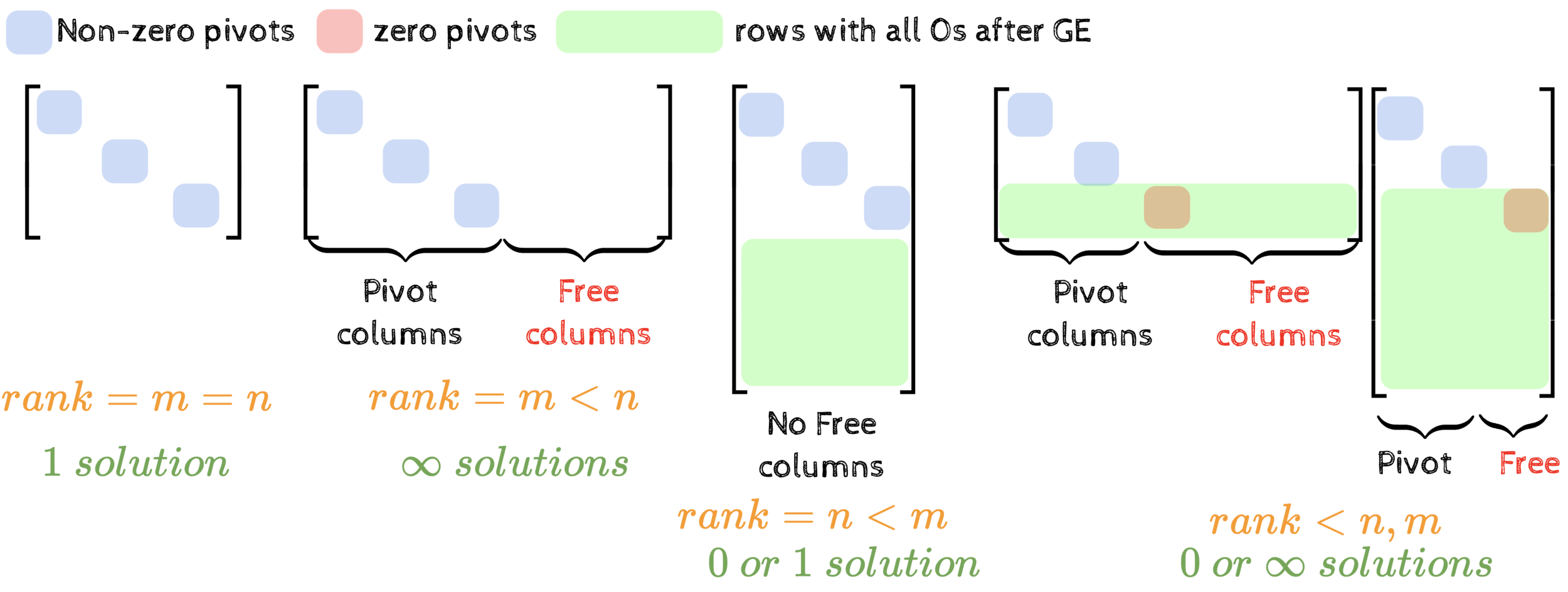
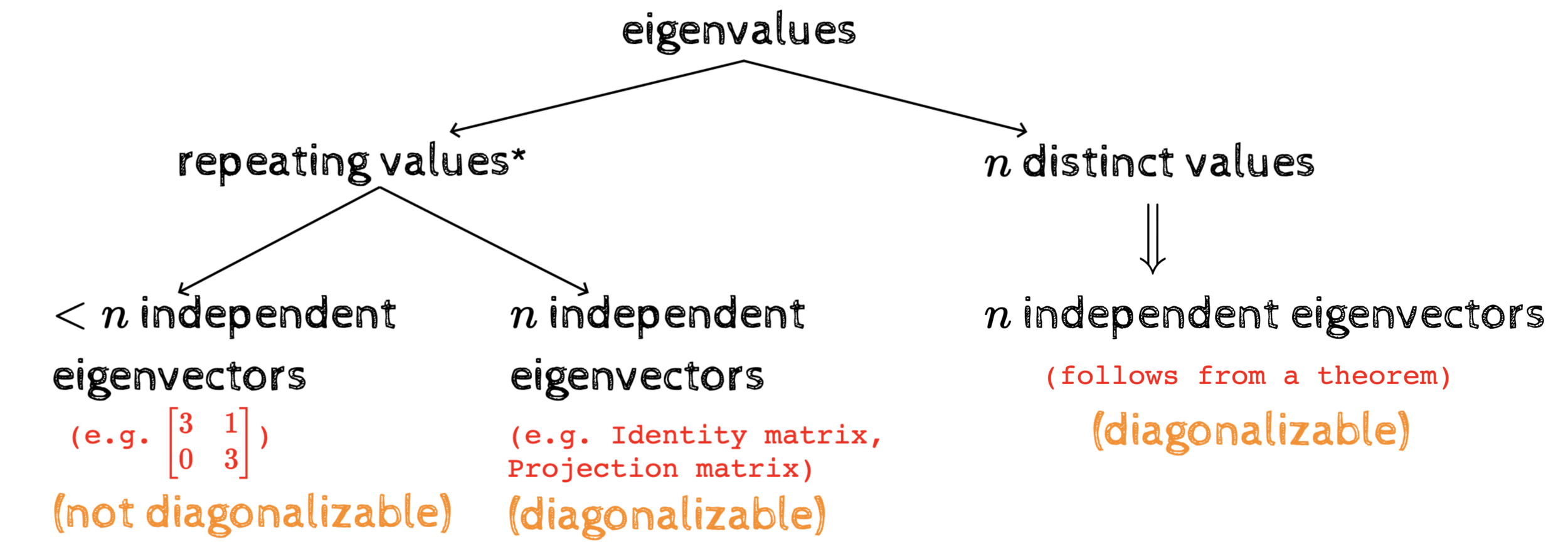
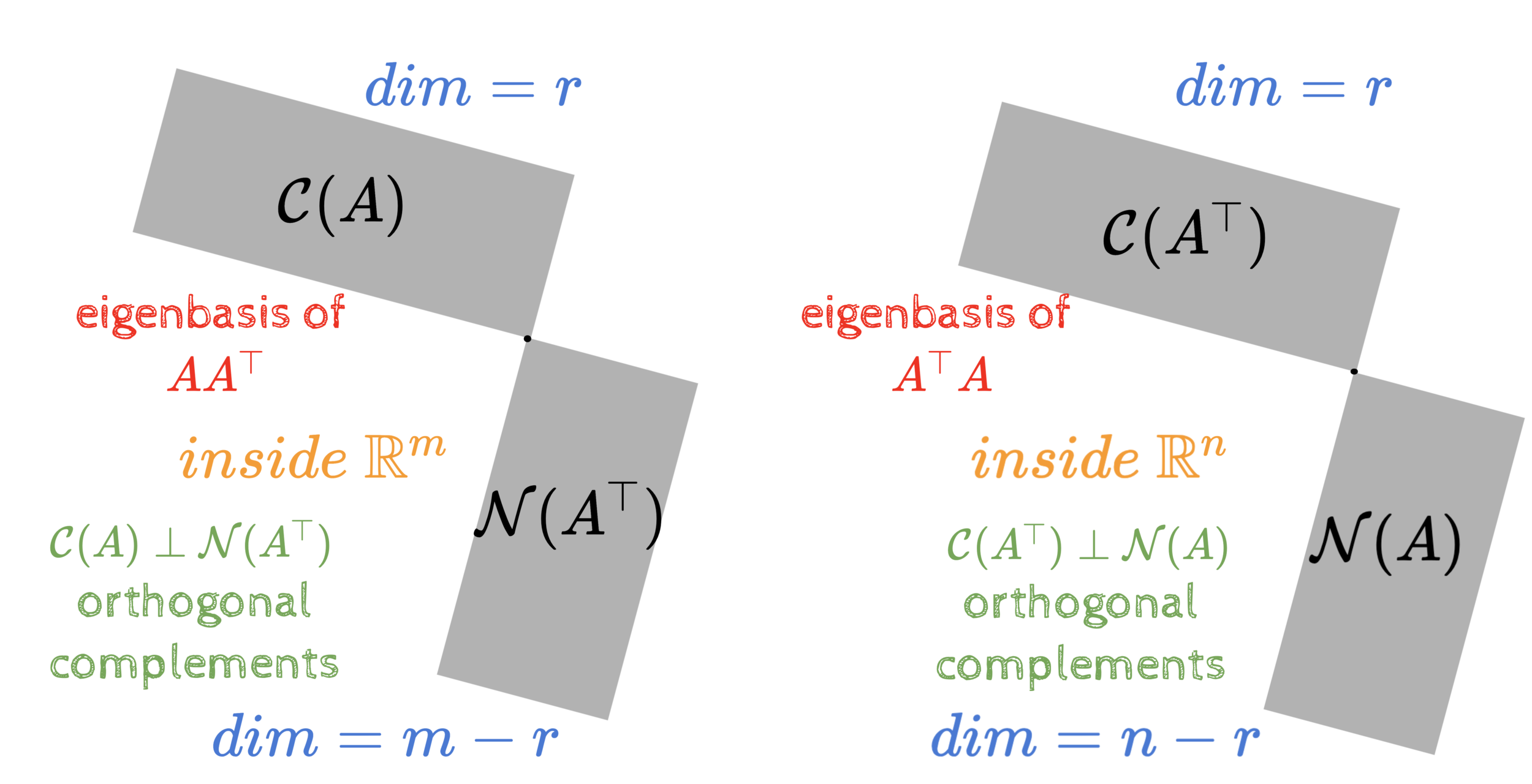
Summary of the course
(in 6 great theorems)
Source: Introduction to Linear Algebra, Prof. Gilbert Strang
The full story
(How would you do this in practice?)
Compute the n eigen vectors of X TX
Sort them according to the corresponding eigenvalues
Retain only those eigenvectors corresponding to the top-k eigenvalues
Project the data onto these k eigenvectors
We know that n such vectors will exist since it is a symmetric matrix
These are called the principal components
Heuristics: k=50,100 or choose k such that λk/λmax > t
CS6015: Linear Algebra and Random Processes Lecture 21: Principal Component Analysis (the math)
Copy of Copy of CS6015: Lecture 21
By Madhura Pande cs17s031
Copy of Copy of CS6015: Lecture 21
Lecture 21: Principal Component Analysis (the math)
- 531
