1.6 The Perceptron Model

Your first model with weights

Recap: MP Neuron

What did we see in the previous chapter?

(c) One Fourth Labs

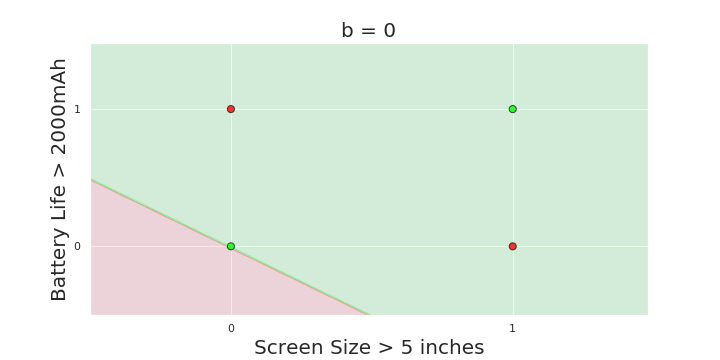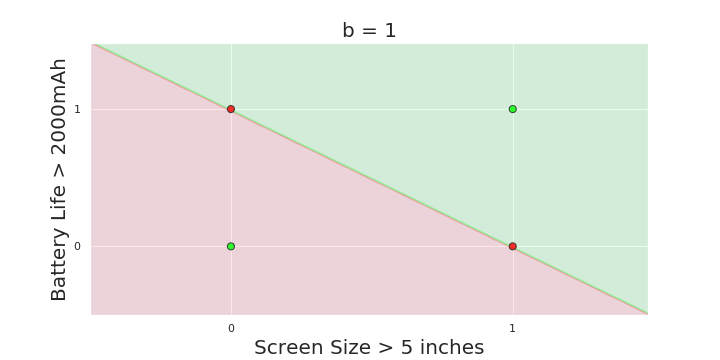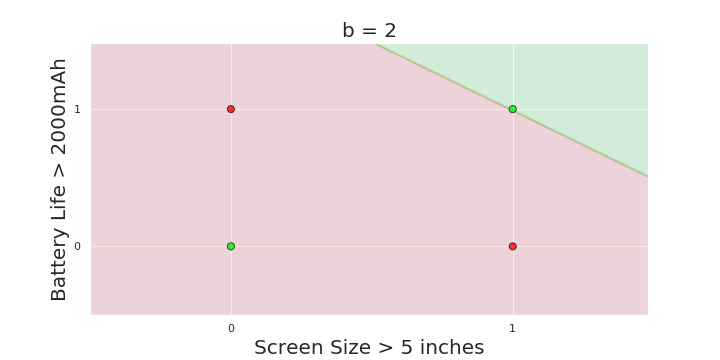
Screen size (>5 in) 1 0 1 1 1 0 1 0 1 0
Battery (>2000mAh) 0 0 0 1 0 1 1 1 1 0
Like 1 0 1 0 1 1 0 1 0 0
\hat{y}
y^\hat{y}
x_1
x1x_1
x_2
x2x_2
b
bb
\hat{y}=\sum_{i=1}^n x_i \gt b
y^=∑i=1nxi>b\hat{y}=\sum_{i=1}^n x_i \gt b

Boolean inputs

Boolean output

Linear

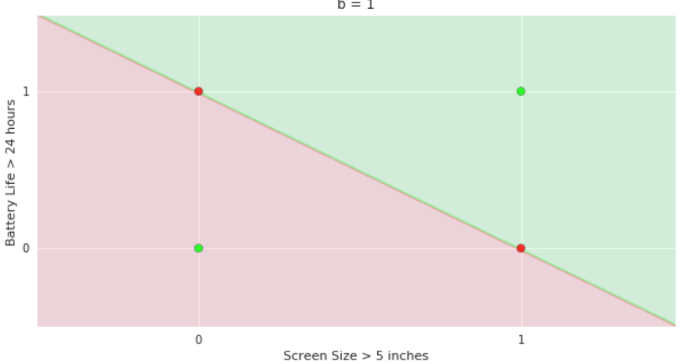
Fixed Slope

Few possible intercepts (b's)

The Road Ahead

What's going to change now ?

(c) One Fourth Labs

\( \{0, 1\} \)

Classification

loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}
Accuracy=Number of correct predictionsTotal number of predictionsAccuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Loss

Model

Data

Task

Evaluation

Learning

Linear

Only one parameter, b

Real inputs

Boolean output

Brute force

Boolean inputs

loss = \sum_i max(0,1-y_i*\hat{y_i})
loss=∑imax(0,1−yi∗yi^)loss = \sum_i max(0,1-y_i*\hat{y_i})

Our 1st learning algorithm

Weights for every input

Data and Task

What kind of data and tasks can Perceptron process ?

(c) One Fourth Labs

Real inputs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size (inches) 5.8 6.18 5.84 6.2 5.9 6.26 4.7 6.41 5.5
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 1960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0
Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (<160g) 1 0 1 0 0 0 1 0 0
Screen size (<5.9 in) 1 0 1 0 1 0 1 0 1
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(>3500mAh) 0 0 0 1 0 1 0 1 0
Price > 20k 0 1 1 0 0 0 1 1 1
Like (y) 1 0 1 0 1 1 0 1 0

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size (inches) 5.8 6.18 5.84 6.2 5.9 6.26 4.7 6.41 5.5
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 1960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0
screen size
5.8
6.18
5.84
6.2
5.9
6.26
4.7
6.41
5.5
screen size
0.64
0.87
0.67
0.88
0.7
0.91
0
1
0.47

min

max

Standardization formula

x' = \frac{x-min}{max-min}
x′=x−minmax−minx&#x27; = \frac{x-min}{max-min}
Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 1960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0
battery
3060
3500
3060
5000
3000
4000
1960
3700
3260
battery
0.36
0.51
0.36
1
0.34
0.67
0
0.57
0.43

min

max

Data Preparation

Can the data be used as it is ?

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 138 185 170
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery 0.36 0.51 0.36 1 0.34 0.67 0 0.57 0.43
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0

Data Preparation

Can the data be used as it is ?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight 0.19 0.63 0.33 1 0.36 0.66 0 0.70 0.48
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery 0.36 0.51 0.36 1 0.34 0.67 0 0.57 0.43
Price 0.09 0.63 0.41 0.19 0.06 0 0.72 0.94 1
Like (y) 1 0 1 0 1 1 0 1 0

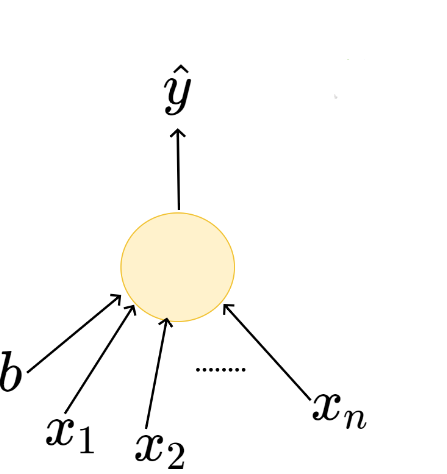
The Model

What is the mathematical model ?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight 0.19 0.63 0.33 1 0.36 0.66 0 0.70 0.48
Screen size 0.64 0.87 0.67 0.88 0.7 0.91 0 1 0.47
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery 0.36 0.51 0.36 1 0.34 0.67 0 0.57 0.43
Price 0.09 0.63 0.41 0.19 0.06 0 0.72 0.94 1
Like (y) 1 0 1 0 1 1 0 1 0

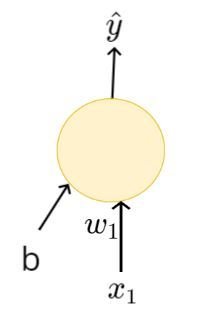
\(x_1\)

b

\(x_n\)

\(\hat{y}\)

\(x_2\)

\(w_1\)

\(w_2\)

\(w_n\)

\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
y^=1 if ∑i=1nwixi≥b\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
\hat{y} = 0 \text{ otherwise }
y^=0 otherwise \hat{y} = 0 \text{ otherwise }

The Model

How is this different from the MP Neuron Model ?

(c) One Fourth Labs

Real inputs

Linear

Weights for each input

Adjustable threshold

Boolean inputs

Linear

Inputs are not weighted

Adjustable threshold

\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
y^=1 if ∑i=1nwixi≥b\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
\hat{y} = 0 \text{ otherwise }
y^=0 otherwise \hat{y} = 0 \text{ otherwise }
\hat{y} = 1 \text{ if } \sum_{i=1}^n x_i \geq b
y^=1 if ∑i=1nxi≥b\hat{y} = 1 \text{ if } \sum_{i=1}^n x_i \geq b
\hat{y} = 0 \text{ otherwise }
y^=0 otherwise \hat{y} = 0 \text{ otherwise }

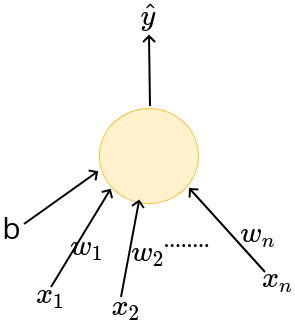
MP Neuron 

Perceptron

The Model

What do weights allow us to do ?

(c) One Fourth Labs

Launch (within 6 months) 0 1 1 0 0 1 0 1 1
Weight (g) 151 180 160 205 162 182 158 185 170
Screen size (inches) 5.8 6.18 5.84 6.2 5.9 6.26 5.7 6.41 5.5
dual sim 1 1 0 0 0 1 0 1 0
Internal memory (>= 64 GB, 4GB RAM) 1 1 1 1 1 1 1 1 1
NFC 0 1 1 0 1 0 1 1 1
Radio 1 0 0 1 1 1 0 0 0
Battery(mAh) 3060 3500 3060 5000 3000 4000 2960 3700 3260
Price (INR) 15k 32k 25k 18k 14k 12k 35k 42k 44k
Like (y) 1 0 1 0 1 1 0 1 0

\(x_1\)

b

\(x_n\)

\(\hat{y}\)

\(x_2\)

\(w_1\)

\(w_2\)

\(w_n\)

\(w_{price} \rightarrow -ve\)

Like  \(\alpha  \frac{1}{price}\)

\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
y^=1 if ∑i=1nwixi≥b\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
\hat{y} = 0 \text{ otherwise }
y^=0 otherwise \hat{y} = 0 \text{ otherwise }

Some Math fundae

Can we write the perceptron model slightly more compactly?

(c) One Fourth Labs

x : [0, 0.19, 0.64, 1, 1, 0]

w: [0.3, 0.4, -0.3, 0.1, 0.5]

 \(\textbf{x} \in R^5\)

 \(\textbf{w} \in R^5\)

\( \vec{x} \)

\( \vec{w} \)

\(\textbf{x}.\textbf{w}\) = ?

\(\textbf{x}.\textbf{w} = x_1.w_1 + x_2.w_2 + ... x_n.w_n\)

= \sum_{i=1}^n x_i.w_i
=∑i=1nxi.wi= \sum_{i=1}^n x_i.w_i
\hat{y}= 1 \text{ (if } \textbf{x}.\textbf{w} \geq b)
y^=1 (if x.w≥b)\hat{y}= 1 \text{ (if } \textbf{x}.\textbf{w} \geq b)
\hat{y}= 0 \text{ (otherwise)}
y^=0 (otherwise)\hat{y}= 0 \text{ (otherwise)}

\(x_1\)

b

\(x_n\)

\(\hat{y}\)

\(x_2\)

\(w_1\)

\(w_2\)

\(w_n\)

\( \textbf{x} \)

\( \textbf{w} \)

\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
y^=1 if ∑i=1nwixi≥b\hat{y} = 1 \text{ if } \sum_{i=1}^n w_i x_i \geq b
\hat{y} = 0 \text{ otherwise }
y^=0 otherwise \hat{y} = 0 \text{ otherwise }

\(\textbf{x}.\textbf{w} \)

= \sum_{i=1}^n x_i.w_i
=∑i=1nxi.wi= \sum_{i=1}^n x_i.w_i

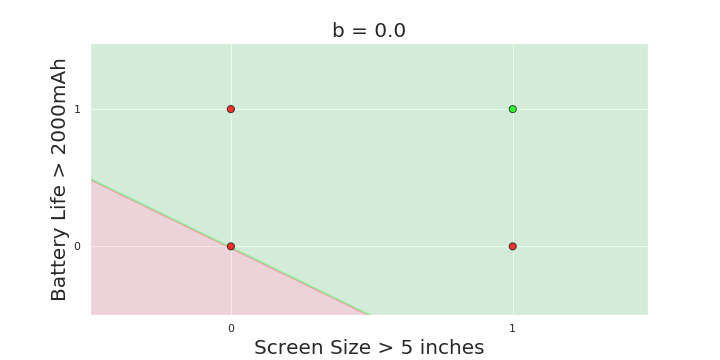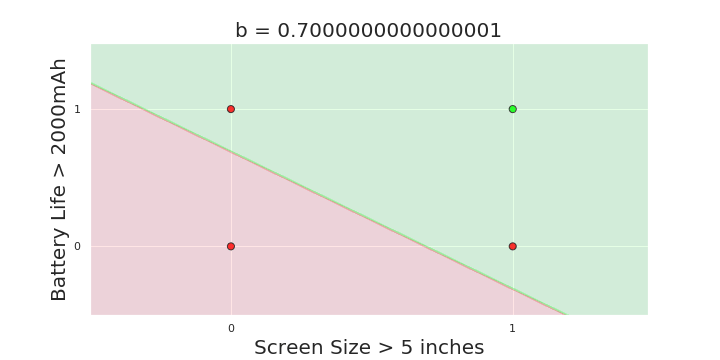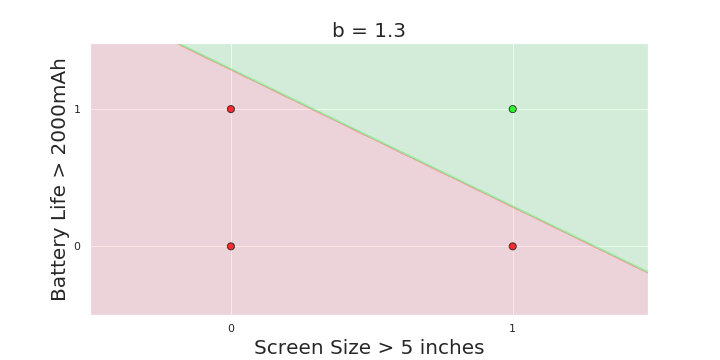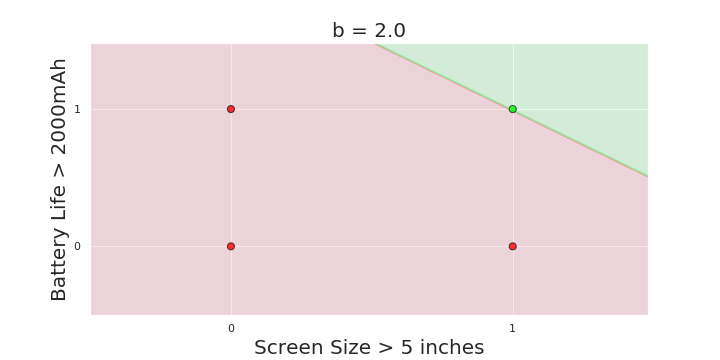
The Model

What is the geometric interpretation of the model ?

(c) One Fourth Labs

More freedom

MP neuron

Perceptron

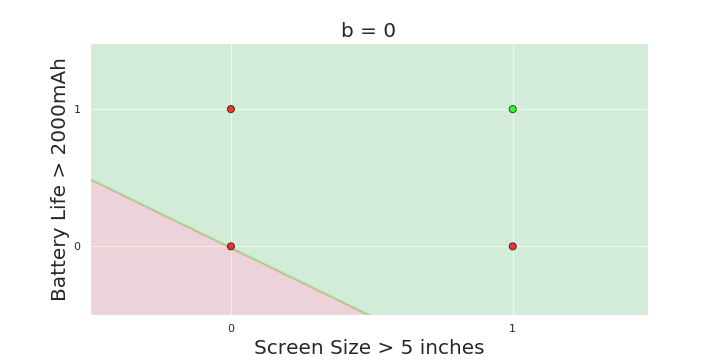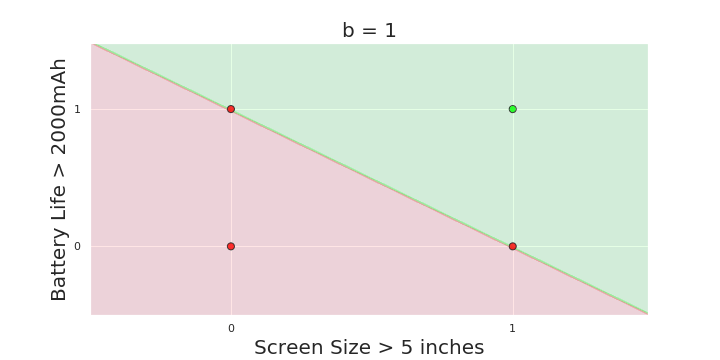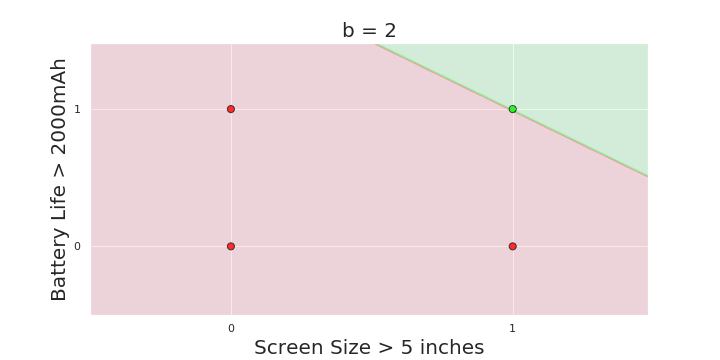
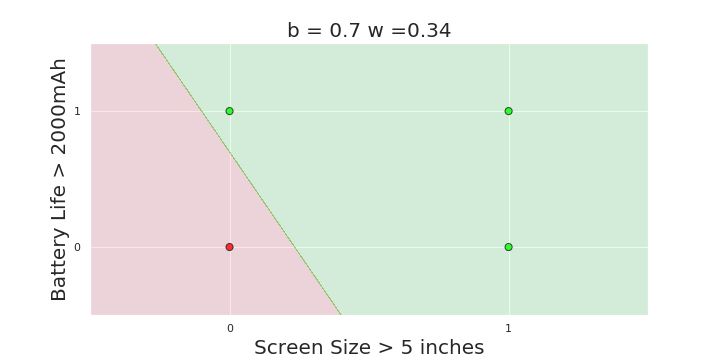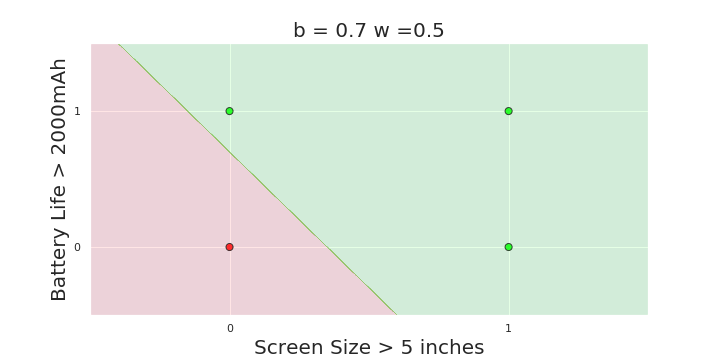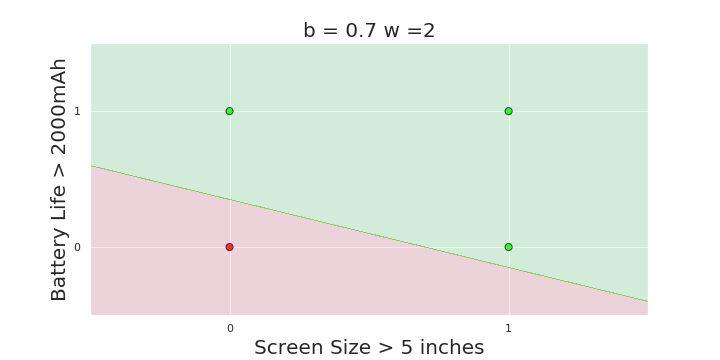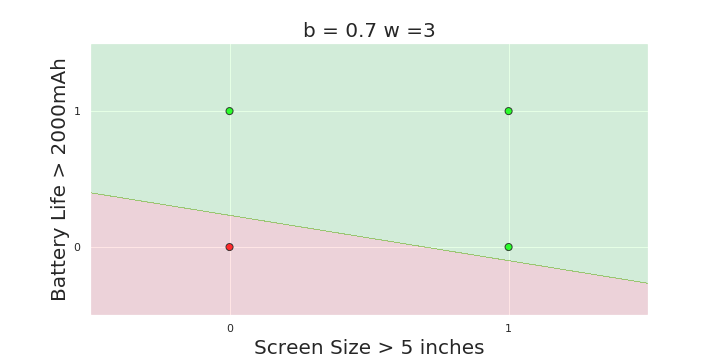
The Model

Why is more freedom important ?

(c) One Fourth Labs

More freedom

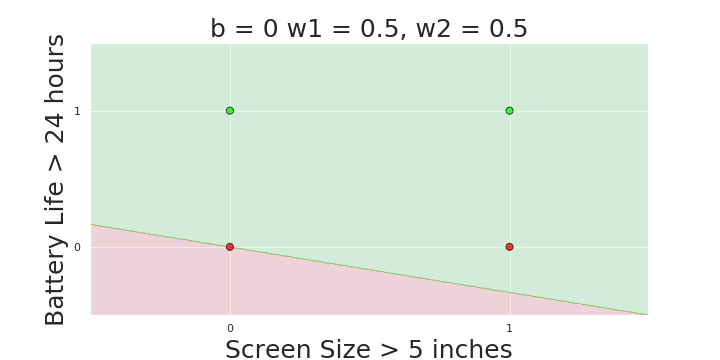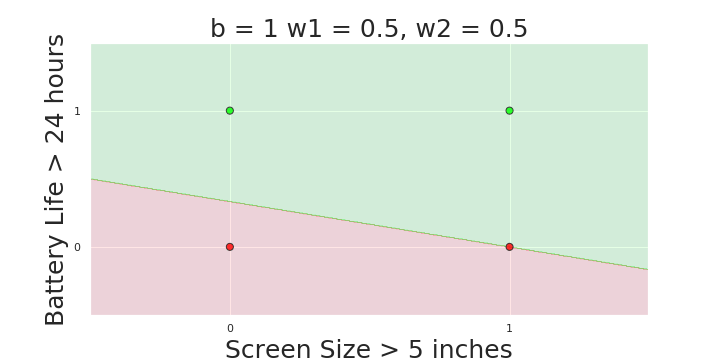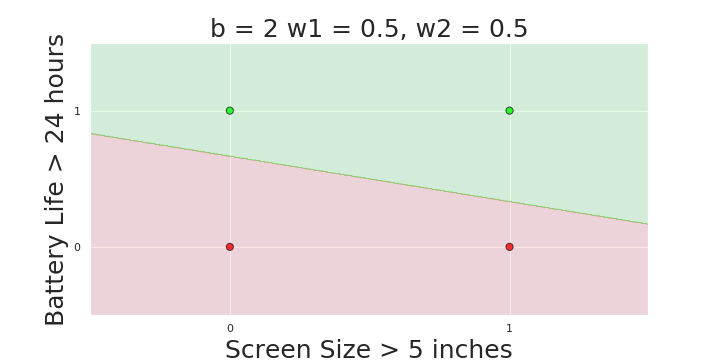
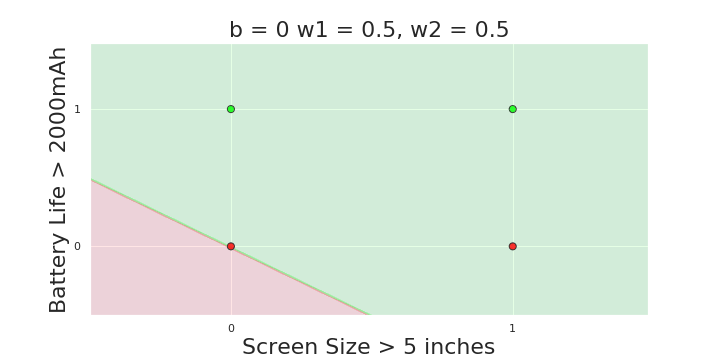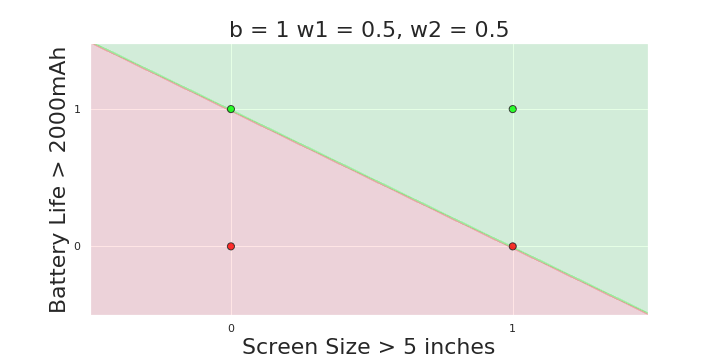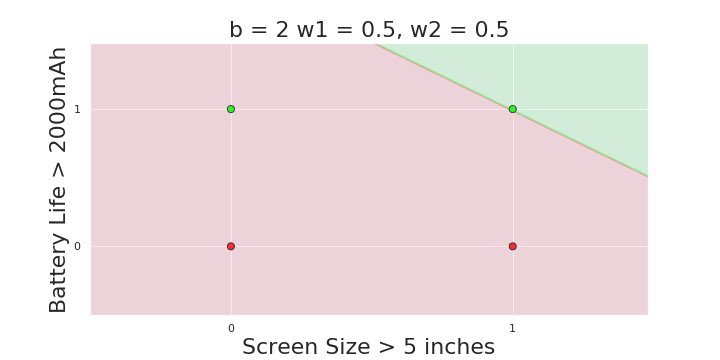
MP neuron

Perceptron

The Model

Is this all the freedom that we need ?

(c) One Fourth Labs

We want even more freedom

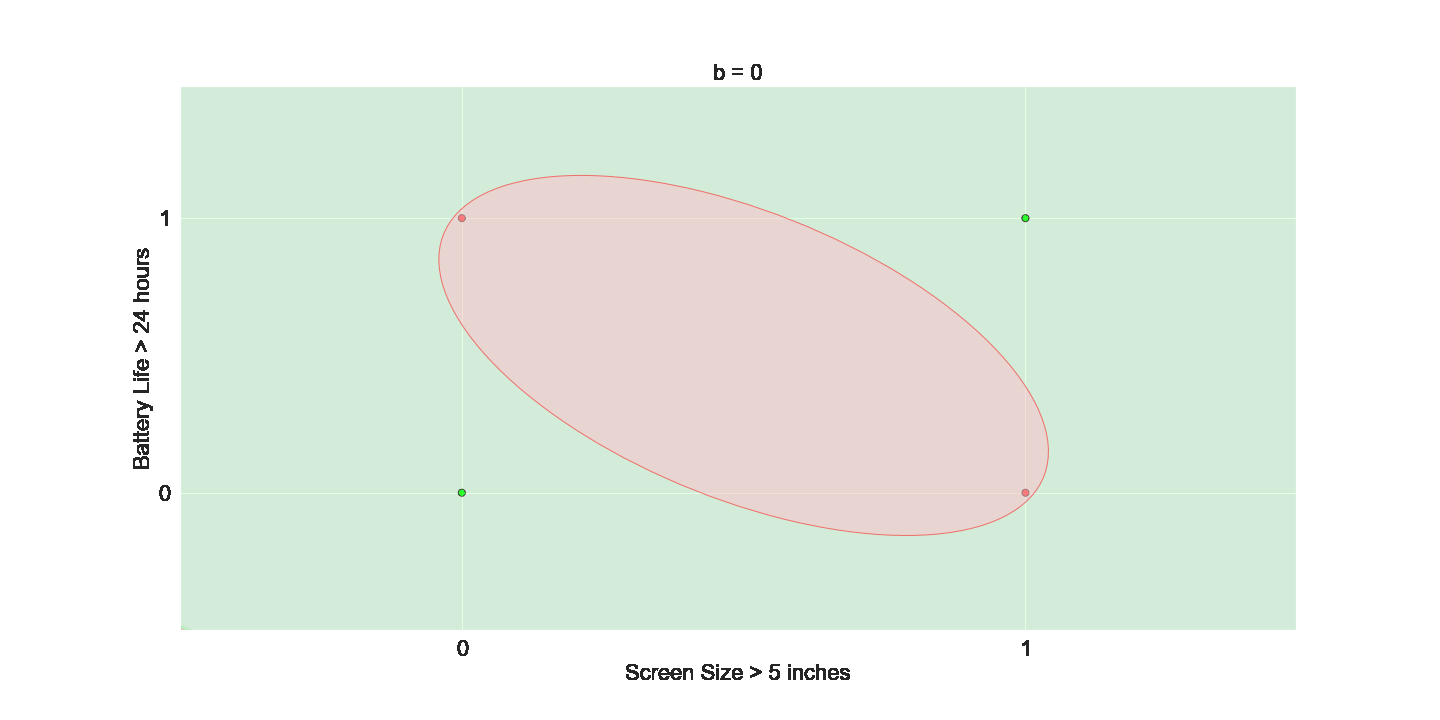
The Model

What if we have more than 2 dimensions ?

(c) One Fourth Labs

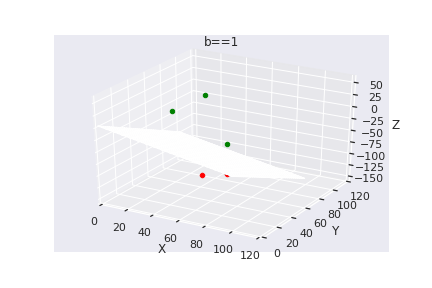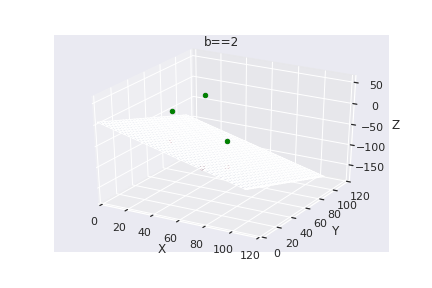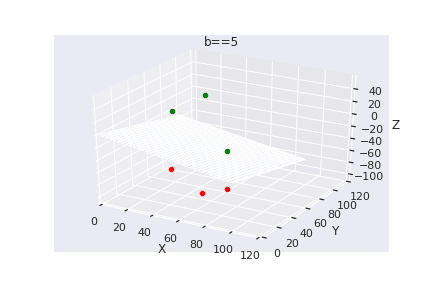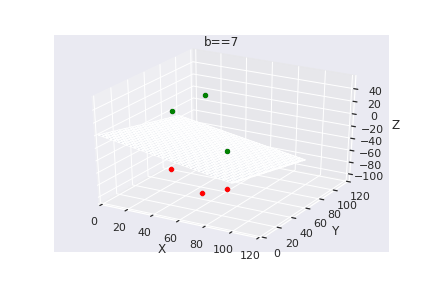
Loss Function

What is the loss function that you use for this model ?

(c) One Fourth Labs

Weight Screen size Like
0.19 0.64 1
0.63 0.87 1
0.33 0.67 0
1 0.88 0
Weight Screen size Like Loss
0.19 0.64 1 1 0
0.63 0.87 1 0 1
0.33 0.67 0 1 1
1 0.88 0 0 0
\hat{y}
y^\hat{y}
(y)
(y)(y)
L=0,\text{ if } y=\hat{y}
L=0, if y=y^L=0,\text{ if } y=\hat{y}
=1,otherwise
=1,otherwise=1,otherwise
L = \textbf{1}_{(y-\hat{y})}
L=1(y−y^)L = \textbf{1}_{(y-\hat{y})}

Q. What is the purpose of the loss function ?

A. To tell the model that some correction needs to be done!

Q. How ?

A. We will see soon

Loss Function

How is this different from the squared error loss function ?

(c) One Fourth Labs

Squared error loss is equivalent to perceptron loss when the outputs are boolean.

Weight Screen size Like
0.19 0.64 1 1
0.63 0.87 1 0
0.33 0.67 0 1
1 0.88 0 0
(y)
(y)(y)
\hat{y}
y^\hat{y}
Perceptron Loss Squared Error Loss

0

0

0

0

1

1

1

1

Perceptron loss = 

Squared Error loss = 

\textbf{1}_{(y-\hat{y})}
1(y−y^)\textbf{1}_{(y-\hat{y})}
(y-\hat{y})^2
(y−y^)2(y-\hat{y})^2

Loss Function

Can we plot the loss function ?

(c) One Fourth Labs

Price

 		 Like
0.2 1
0.4 1
0.6 0
0.7 0
0.45 1
(y)
(y)(y)
Price Like     (w=0.5,b=0.3) Loss
0.2 1 1 0
0.4 1 1 0
0.6 0 1 1
0.7 0 0 0
0.45 1 1 0
\hat{y}
y^\hat{y}
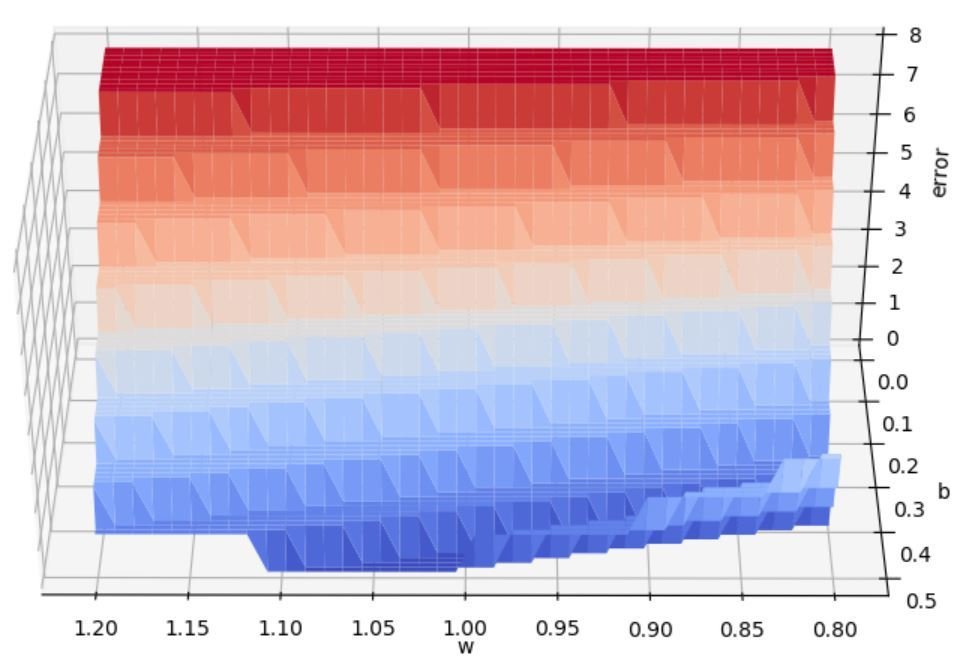
Price Like   (w=0.8,b=0.1) Loss
0.2 1 0 1
0.4 1 0 1
0.6 0 0 0
0.7 0 0 0
0.45 1 0 1
Price Like   (w=1,b=0.5) Loss
0.2 1 1 0
0.4 1 1 0
0.6 0 0 0
0.7 0 0 0
0.45 1 1 0

Error = 1

Error = 3

Error = 0

Learning Algorithm

 

What is the typical recipe for learning parameters of a model ?

(c) One Fourth Labs

Initialise 

\(w_1, w_2, b \)

Iterate over data:

\( \mathscr{L}  = compute\_loss(x_i) \)

\( update(w_1, w_2, b, \mathscr{L}) \)

till satisfied

\(\mathbf{w} = [w_1, w_2] \)

Weight Screen size Like
0.19 0.64 1
0.63 0.87 1
0.33 0.67 0
1 0.88 0

Learning Algorithm

 

What does the perceptron learning algorithm look like ?

Initialize w randomly
    while !convergence do
        Pick random x ∈ P U N
	    if y_i == 1 and w.x < b then
	         w = w + x 
	         b = b + 1
	    end
	    if y_i == 0 and w.x ≥ b then
		 w = w − x 
		 b = b - 1
	    end
    end
/*the algorithm converges when all the
inputs are classified correctly */
\hat{y}=\sum_{i=1}^n w_i x_i \geq b
y^=∑i=1nwixi≥b\hat{y}=\sum_{i=1}^n w_i x_i \geq b
\hat{y}= 1 \text{ (if } \vec{x}.\vec{w} \geq b)
y^=1 (if x⃗.w⃗≥b)\hat{y}= 1 \text{ (if } \vec{x}.\vec{w} \geq b)
\hat{y}= 0 \text{ (otherwise)}
y^=0 (otherwise)\hat{y}= 0 \text{ (otherwise)}

X is also a vector!

[0.19, 0.67]
[0.19,0.67][0.19, 0.67]

Learning Algorithm

 

Can we see this algorithm in action ?

(c) One Fourth Labs

Initialize w randomly
    while !convergence do
        Pick random x ∈ P U N
	    if y_i == 1 and w.x < b then
	         w = w + x 
	         b = b + 1
	    end
	    if y_i == 0 and w.x ≥ b then
		 w = w − x 
		 b = b - 1
	    end
    end
/*the algorithm converges when all the
inputs are classified correctly */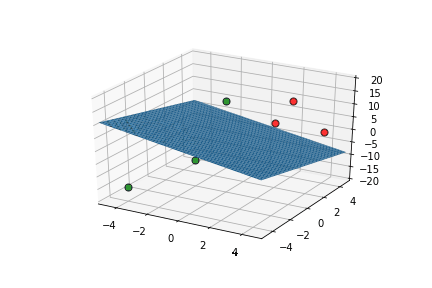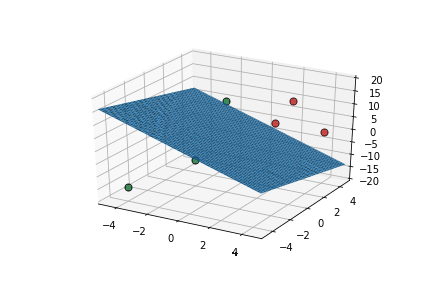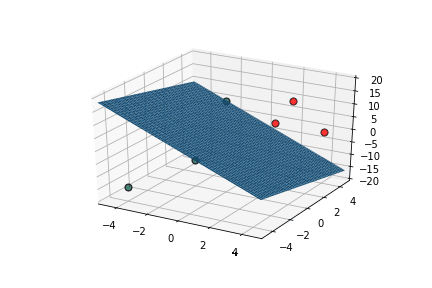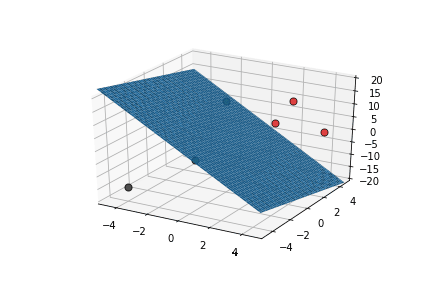
x1 x2 x3
2 2 5 10 1 1
2 4 10 17 1 1
4 4 0 11 1 1
0 0 15 14 1 0
-4 -4 -15 -15 0 0
-2 0 -10 -26 0 0
\vec{x}.\vec{w}-b
x⃗.w⃗−b \vec{x}.\vec{w}-b
\hat{y}
y^\hat{y}
y
yy

This triggers learning!

\hat{y}= 1 \text{ (if } \vec{x}.\vec{w} \geq b)
y^=1 (if x⃗.w⃗≥b)\hat{y}= 1 \text{ (if } \vec{x}.\vec{w} \geq b)
\hat{y}= 0 \text{ (otherwise)}
y^=0 (otherwise)\hat{y}= 0 \text{ (otherwise)}

Learning Algorithm

 

What is the geometric interpretation of this ?

\hat{y}=\sum_{i=1}^n w_i x_i \geq b
y^=∑i=1nwixi≥b\hat{y}=\sum_{i=1}^n w_i x_i \geq b

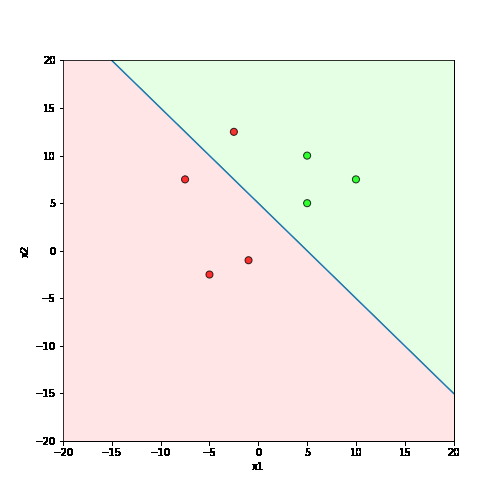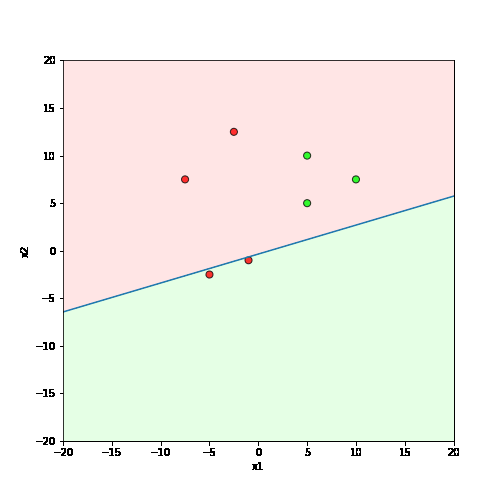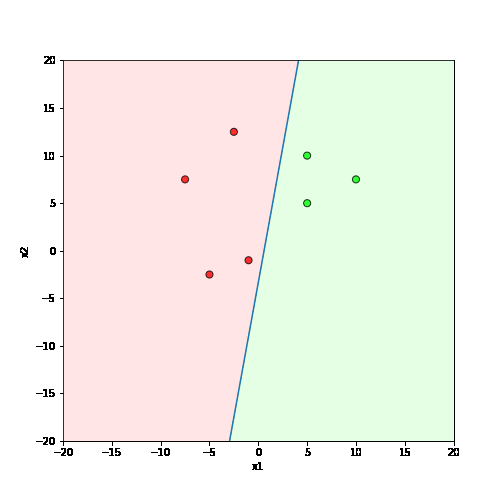
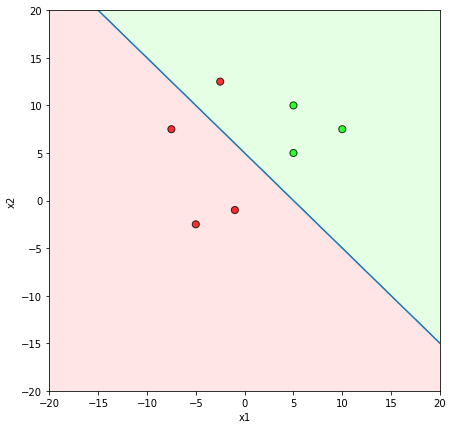
Misclassified

Let's learn!

Initialize w randomly
    while !convergence do
        Pick random x ∈ P U N
	    if y_i == 1 and w.x < b then
	         w = w + x 
	         b = b + 1
	    end
	    if y_i == 0 and w.x ≥ b then
		 w = w − x 
		 b = b - 1
	    end
    end
/*the algorithm converges when all the
inputs are classified correctly */

Learning Algorithm

 

Will this algorithm always work ?

Only if the data is linearly separable

Learning Algorithm

 

Can we prove that it will always work for linearly separable data ?

(c) One Fourth Labs

\mathbf{Definition}: Two \space sets \space P \space and \space N \space of \space points \newline in \space an \space n-dimensional \space space \newline are \space called \space absolutely \space linearly \space separable \newline if \space n + 1 \space real \space P \space numbers \space w_0 , w_1 , ..., w_n \newline exist \space such \space that \space every \space point (x_1 , x_2 , ..., x_n ) ∈ P \space satisfies \newline \sum_{i=1}^n w_i ∗ x_i > w_0 \newline and \space every \space point \space (x_1 , x_2 , ..., x_n ) ∈ N \space satisfies \newline \sum_{i=1}^n w_i ∗ x_i < w_0 \newline \newline \mathbf{Proposition}:If \space the \space sets \space P \space and \space N \space are \space finite \space and \space linearly \space separable.
Definition:Two sets P and N of pointsin an n−dimensional spaceare called absolutely linearly separableif n+1 real P numbers w0,w1,...,wnexist such that every point(x1,x2,...,xn)∈P satisfies∑i=1nwi∗xi&gt;w0and every point (x1,x2,...,xn)∈N satisfies∑i=1nwi∗xi&lt;w0Proposition:If the sets P and N are finite and linearly separable.\mathbf{Definition}: Two \space sets \space P \space and \space N \space of \space points \newline in \space an \space n-dimensional \space space \newline are \space called \space absolutely \space linearly \space separable \newline if \space n + 1 \space real \space P \space numbers \space w_0 , w_1 , ..., w_n \newline exist \space such \space that \space every \space point (x_1 , x_2 , ..., x_n ) ∈ P \space satisfies \newline \sum_{i=1}^n w_i ∗ x_i &gt; w_0 \newline and \space every \space point \space (x_1 , x_2 , ..., x_n ) ∈ N \space satisfies \newline \sum_{i=1}^n w_i ∗ x_i &lt; w_0 \newline \newline \mathbf{Proposition}:If \space the \space sets \space P \space and \space N \space are \space finite \space and \space linearly \space separable.

Learning Algorithm

 

What does "till satisfied" mean ?

(c) One Fourth Labs

Initialise 

\(w_1, w_2, b \)

Iterate over data:

\( \mathscr{L}  = compute\_loss(x_i) \)

\( update(w_1, w_2, b, \mathscr{L}) \)

till satisfied

\( total\_loss  = 0 \)

\( total\_loss  += \mathscr{L} \)

till total loss becomes 0

till total loss becomes < \( \epsilon \)

till number of iterations exceeds k (say 100)

Evaluation

 

How do you check the performance of the perceptron model?

(c) One Fourth Labs

Same slide as that in MP neuron

Take-aways

So will you use MP neuron?

(c) One Fourth Labs

 

\( \in \mathbb{R} \)

Classification

loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}
Accuracy=Number of correct predictionsTotal number of predictionsAccuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Loss

Model

Data

Task

Evaluation

Learning

Real inputs

Boolean Output

An Eye on the Capstone project

How is perceptron related to the capstone project ?

(c) One Fourth Labs

Show the 6 jars at the top (again can be small)

 

\( \{0, 1\} \)

\( \in \mathbb{R} \)

 

Show that the signboard image can be represented as real numbers

Boolean

 

text/no-text

Show a plot with all text images on one side and non-text on another

show squared error loss

show perceptronlearning algorithm

show accuracy formula

and show a small matrix below with some ticks and crossed and show how accuracy will be calculated

The simplest model for binary classification

An Eye on the Capstone project

How is perceptron related to the capstone project ?

(c) One Fourth Labs

Show the 6 jars at the top (again can be small)

 

\( \{0, 1\} \)

\( \in \mathbb{R} \)

 

Show that the signboard image can be represented as real numbers

Boolean

 

text/no-text

Show a plot with all text images on one side and non-text on another

show squared error loss

show perceptronlearning algorithm

show accuracy formula

and show a small matrix below with some ticks and crossed and show how accuracy will be calculated

The simplest model for binary classification

\( \{0, 1\} \)

Boolean

loss = \sum_i (y_i-\hat{y_i})^2
loss=∑i(yi−yi^)2loss = \sum_i (y_i-\hat{y_i})^2
Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}
Accuracy=Number of correct predictionsTotal number of predictionsAccuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}

Loss

Model

Data

Task

Evaluation

Learning

Linear

Only one parameter, b

Real inputs

Boolean output

Brute force

Boolean inputs

loss = \sum_i max(0,1-y_i*\hat{y_i})
loss=∑imax(0,1−yi∗yi^)loss = \sum_i max(0,1-y_i*\hat{y_i})

Our 1st learning algorithm

Weights for every input

Assignments

 

How do you view the learning process ?

(c) One Fourth Labs

Assignment: Give some data including negative values and ask them to standardize it

Copy for Preksha's 1.6 Perceptron

By Madhura Pande cs17s031

Source: preksha nema

Copy for Preksha's 1.6 Perceptron

  • 537

More from Madhura Pande cs17s031