Calibration and synchronization

of large-scale low-cost sensor networks

New Scenario

Large scale sensor deployment in the distribution networks

New Energetic Scenario - New Applications

State Estimation

Topology Detection

Monitoring

Need for large-scale distributed sensing

Challenges

  • Low cost / low accuracy sensors
  • Communication constraints
  • Scalability of the monitoring infrastructure

2. Possible issues...

  • Low accuracy

  • Low precision

3. Due to...

  • Systematic measurement error

  • Synchronization error

  • Sensors parametric uncertainty

Similar Problem: Large scale WSN

1. Used for...

  • State estimation
  • Monitoring and control

Solution: Sensor calibration / sync errors compensation

Averaging useless!!

Distributed sensor blind calibration*

\mathrm{error\ [dBm]}
error [dBm]\mathrm{error\ [dBm]}
\mathrm{Asymmetric\ error\ before\ and\ after\ the\ offset\ correction}
Asymmetric error before and after the offset correction\mathrm{Asymmetric\ error\ before\ and\ after\ the\ offset\ correction}

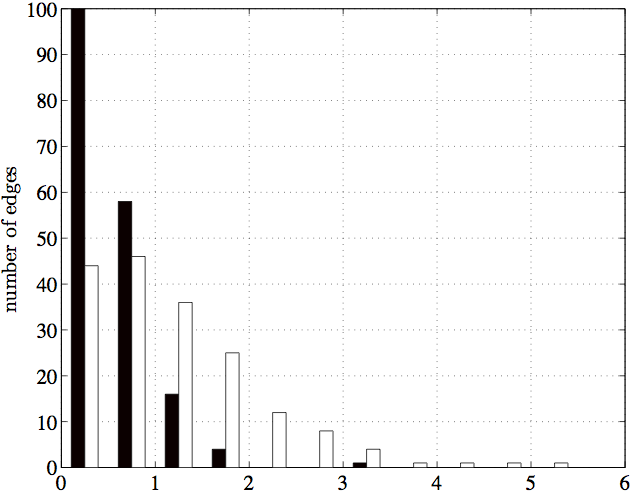
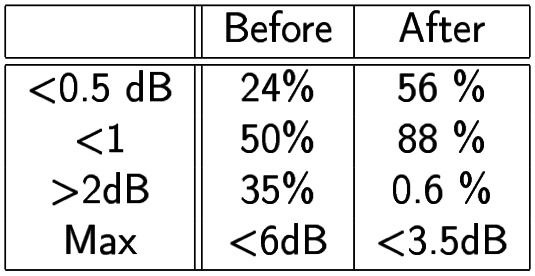
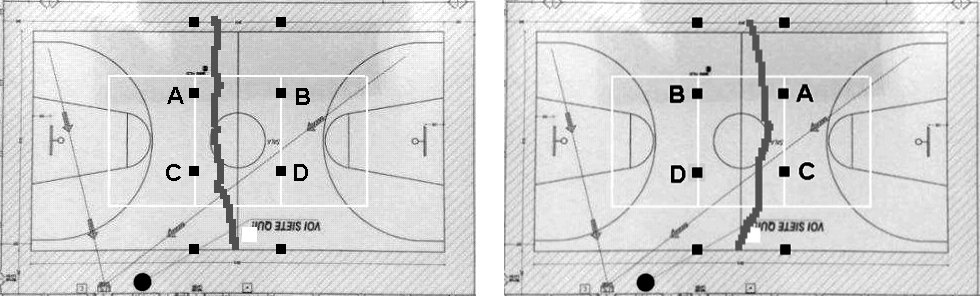
Effect of systematic errors when estimating distances

*no dependence on controlled stimuli/reference/high-fidelity groundtruth data

Sync Error Compensation

GPS

GPS

\begin{matrix} v_{\mathrm{true}}^i + n^i_v\\ \theta_{\mathrm{true}}^i + n^i_\theta \end{matrix}
vtruei+nviθtruei+nθi\begin{matrix} v_{\mathrm{true}}^i + n^i_v\\ \theta_{\mathrm{true}}^i + n^i_\theta \end{matrix}
\begin{matrix} v_{\mathrm{true}}^j + n_v^j\\ \theta_{\mathrm{true}}^j + n_\theta^j \end{matrix}
vtruej+nvjθtruej+nθj\begin{matrix} v_{\mathrm{true}}^j + n_v^j\\ \theta_{\mathrm{true}}^j + n_\theta^j \end{matrix}

Low Cost Sensor

\begin{matrix} v_{\mathrm{true}}^k + n^k_v\\ \theta_{\mathrm{true}}^k + n^k_\theta + \overline{\theta}_k \end{matrix}
vtruek+nvkθtruek+nθk+θ‾k\begin{matrix} v_{\mathrm{true}}^k + n^k_v\\ \theta_{\mathrm{true}}^k + n^k_\theta + \overline{\theta}_k \end{matrix}

Low Cost Sensor

\begin{matrix} v_{\mathrm{true}}^\ell + n^\ell_v\\ \theta_{\mathrm{true}}^\ell + n^\ell_\theta + \overline{\theta}_\ell \end{matrix}
vtrueℓ+nvℓθtrueℓ+nθℓ+θ‾ℓ\begin{matrix} v_{\mathrm{true}}^\ell + n^\ell_v\\ \theta_{\mathrm{true}}^\ell + n^\ell_\theta + \overline{\theta}_\ell \end{matrix}

Low Cost Sensors clock affected by systematic (constant) sync error

Compensation by leveraging on error model 

\overline{\theta}
θ‾\overline{\theta}

Problem Formulation

Measurement model (at time instant t)

y(t) = Hx(t) + w + e(t)
y(t)=Hx(t)+w+e(t)y(t) = Hx(t) + w + e(t)

where

  • ​y, measurement
  • x, state
  • H, meas. matrix
  • w, offset error (constant over time)
  • e, random noise ~ 
\mathcal{N}(0,\sigma^2)
N(0,σ2)\mathcal{N}(0,\sigma^2)

Collecting a series of measurements (from t to t+T)

Y = HX + w \mathbb{1}^T + E
Y=HX+w1T+EY = HX + w \mathbb{1}^T + E

Then,

\min_{X,w} \| w \| + \| Y - HX - w\mathbb{1}^T\|_R
minX,w∥w∥+∥Y−HX−w1T∥R\min_{X,w} \| w \| + \| Y - HX - w\mathbb{1}^T\|_R
s.t.\ \ AX = B
s.t.  AX=Bs.t.\ \ AX = B

(linearized power flow model)

Solver/Solution characteristics

1. ​Scalable: possibility to easily adapt the solution to networks changing in size

 

2. Recursive: capability to adapt the solution as new measurements arrive (on-line)

 

3. Low Communication Requirements: minimum exchange of information needed in order to perform the compensation

What do we need?

A concrete and consistent measurement model

the closer the model* to the reality the better and reliable the calibration

Real data to test the algorithm

validate the effectiveness of the algorithm for its practical implementation

*blind calibration needs reliable model

Algorithm Structure

Collect data

Data cleaning and processing 

Offset estimation

(Error model)

Go to

state estimation 

& 

control

Sensors Calibration

Logs & statistical report

Sensor calibration and synchronization

By marco todescato

Made with Slides.com

Sensor calibration and synchronization

Presentation to briefly present issues and approach to sensor calibration

  • 162

More from marco todescato