COURSE OVERVIEW
Why learn Calculus?
What we will talk about in this class, a lot.
- Graphs
- Cryptocurrency Graphs
- Black Holes, limits and infinity
- Graphs of functions
- change
- Graphs
- Applications in business administration, finance, engineering and industrial design.
Why learn Mathematics?
1. You don’t have to learn Mathematics — most of the time —.
You do, however, need to learn how to deal with failure. Calculus is designed to teach you that. Why?
2. Struggling is important. Failing is important. This class will be your best practice to fail. Do not underestimate failure.
3 If you are obsessed with a grade, then you should start looking for counseling since you will struggle and you will arrive at incorrect answers MANY times. It is just normal. Don't panic. I will guide you through the whole process, and will give you enough resources and quality time to make you succeed if you WANT to succeed.
4. One of the most important things in life is knowing how to recover from failure. Life is full of failures.
5. Because it is a profound personal experience that also stimulates your brain.
Recover
How you recover is one the most important things in life as well.
Do not confuse failure and failing grades. The more you fail in my class the more you will learn and get you a higher grade.
Don’t stigmatize mistakes. Mistakes are key in mathematics.
Algebra is the reason #1 students struggle
The usual trouble that people have with ‘calculus’ is with algebra
Calculus itself is quite easy
I personally think that I make this class extremely easy for everyone to get a 100, but you have to take Calculus seriously.
It is not like any other course you have taken in the past.
Learn from the past
- Students who complain usually fail or do very bad in the class. Students who commit and work hard usually do very good.
- Students who copy homework fail the class. Always. 100% of the time. Last semester 15 failed due to continued plagiarism during the semester.
- Students who ask questions and participate in class usually score the best grades in exams.
- Students who revisit assignments never fail the class.
- Dishonest students never get a point from me. I will never encourage dishonesty in such way.
- Students who miss class, sleep during class or use their phone during class, ALWAYS struggle.
Keys to success in my class
- Take notes in class. Smart notes, not compulsive notes.
- Start you homework ahead of time and workout problems on your own.
- Learn when to ask for help. Do not wait until the end.
- Make many mistakes and fix them. This is key.
- Make yourself notice. Let me see that you are engaged with the class and that you are genuinely trying.
- Cheating does not work in Math, period. Don’t copy. You will fail.
- But the master key is to learn how to deal with failure.
Is time-travelling possible?

Karl Schwartzswild
Black Holes
Remember this guy?
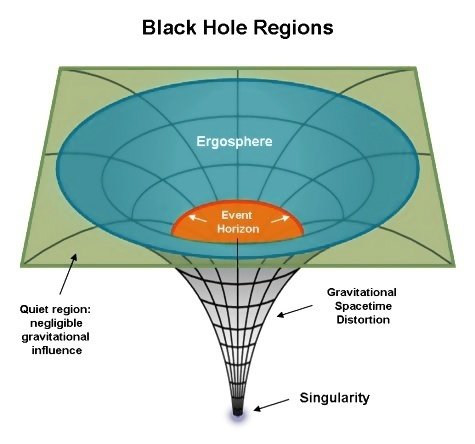
From here it is obvious that:
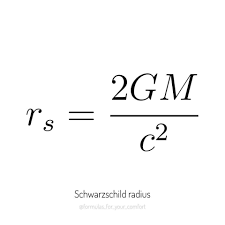
Title Text
The equation tells you this:
1 year spent near the event horizon (rs)
is equal to 1000 years on Earth.

Calculus will help you understand this
You don't need to solve it, nor you will be asked to do something like this.
But you'll understand.
You will also understand how to estimate future value, save a lot of money in your business, design industrial products to maximize profits, and most of all, you will learn to overcome failure and that true effort is the only way of achieving good stuff.
Practice 10 minutes on a daily basis, and you will not need to study for any exam with a 90+ guarantee. Only 10 minutes.
Practice 20 minutes a day and I guarantee you will get a final grade of 100.
Take responsibility
for your learning
for your life
for your relationships with people
for your actions and decisions
for your mistakes
Online HW: Keys
1. Trying one time is not enough. Practice until you get it right. It gets better with time.
2. Engage positively since day 1: ask questions, do all in-class assignments, and participate when prompted.
3. Take mindful and intelligent notes. Do not copy stuff that is already available to you online.
Grading Criteria
In-Class Assignments - 15%
Homework - 15%
Laboratory - 10%
Quizzes - 10%
Demonstration - 10%
Exam 1 - 40%
Introduction to Calculus
2. Limits
1. Precalculus
Continuity
The 0/0 case
Polynomials
Rationals
Limits Involving Infinity
Graphical Approach
Computation examples
Numerical Approach
3. Differentiation
Tangent Lines
Limit Definition
You can use key arrows to move around
4. Optimization
Examples
Stage 1
Stage 2
Stage 3
Stage 4
Functions Quick Review
Tangent Lines
Functions
Quick Review
Limits
\(f(x) = x^3-3x \)
\(f(x) = x^3-3x \)
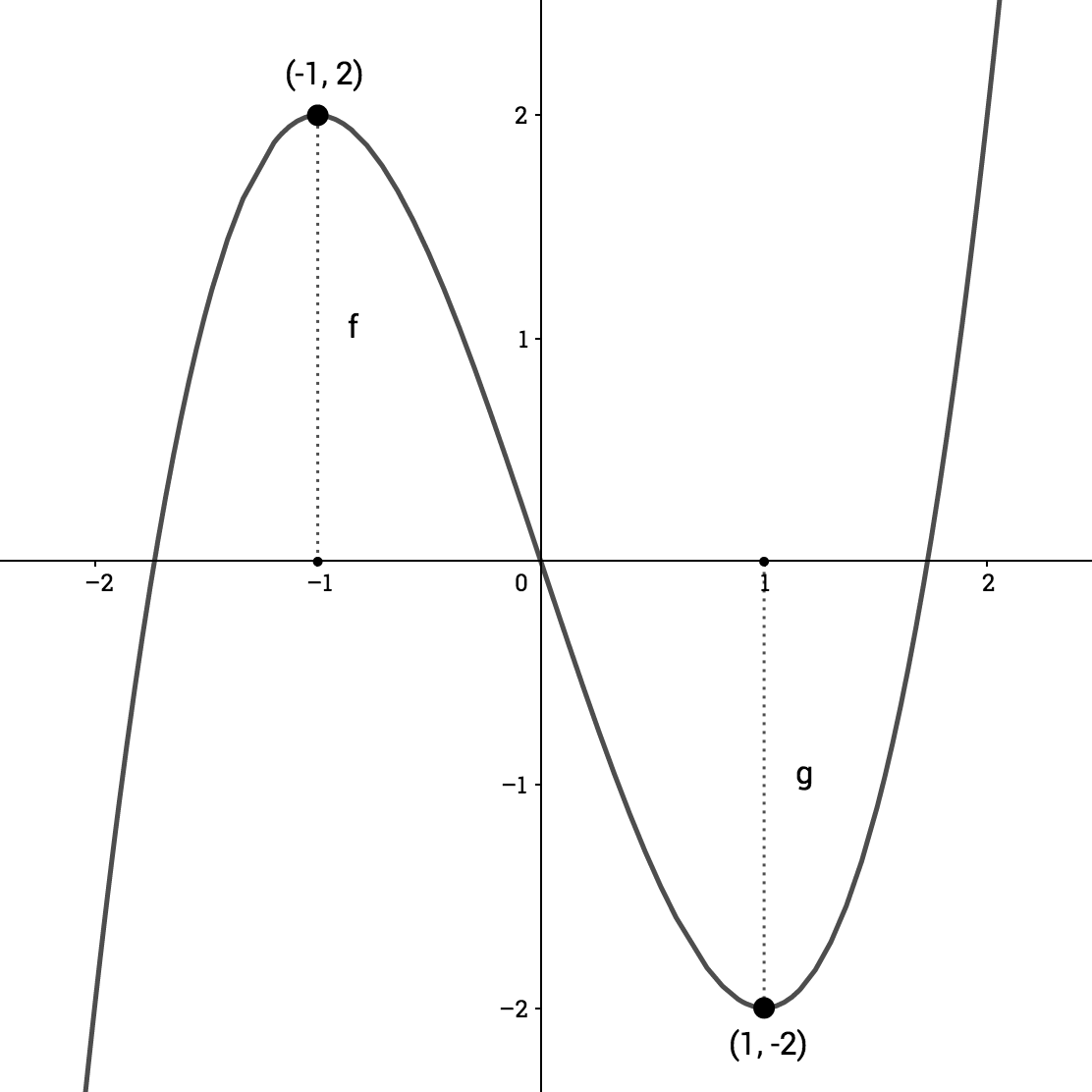
$$ \sqrt{3} $$
$$ -\sqrt{3} $$
Polynomials
Continuous on \((-\infty, \infty)\)
\(y\uparrow\infty\) as \(x\rightarrow \infty\)
\(y\downarrow-\infty\) as \(x\rightarrow -\infty\)
Extrema are going in different directions, so the degree of the leading term must be odd.
\(y\) increases as \(x\rightarrow\infty\), so the leading coefficient must be positive
Example:
What if you wanted to find the maxima and minima of \(p(x)\)?
Using different differentiation techniques it is possible,
and we will use it frequently as we continue our study of Calculus.
$$ = x(x^2 -3) $$
$$x = 0$$ $$ x=\sqrt{3} $$ $$ \ x=-\sqrt{3}$$
$$ \text{We know that } p(x) = x \ (x+\sqrt{3})(x-\sqrt{3})$$
$$ p(x) = x^3 -3x $$
\( \text{Find a polynomial function whose roots (or zeroes) are } x=0, x = \sqrt{3}, x= -\sqrt{3}\)
\(\Leftarrow \) this is the completely factored form of \(p(x)\)
\(\Leftarrow \) This is your fully expanded polynomial \(p(x)\), built from its roots.
$$ \Rightarrow \text{these are called roots or zeros since either } p(0) = 0 ,\ \ p(\sqrt{3})=0 \ \text{ or } \ \ p(-\sqrt{3}) = 0. $$ This also means that \(p(x)\) crosses the \(x\)-axis exactly at these points.
\(\Leftarrow \) multiply the factors to come up with a new form
$$ p(x) = x^3 -3x $$
$$ p'(x) = 3x^2 -3 $$
$$ \Rightarrow p(x) \text{ has a max or min at } x=\pm 1$$
\(\text{ (take the derivative) } \)
\(\text{ (set it equal to 0) } \)
skip
$$ 3x^2 -3=0$$
$$ 3x^2 =3$$
$$ x =\pm 1$$
\(\text{ (the derivative is just a slope, so if } f'(x) = 0 \text{, you must be looking at a max/min point } \)
Rational Functions
$$f(x) = \dfrac{1}{x-1} $$
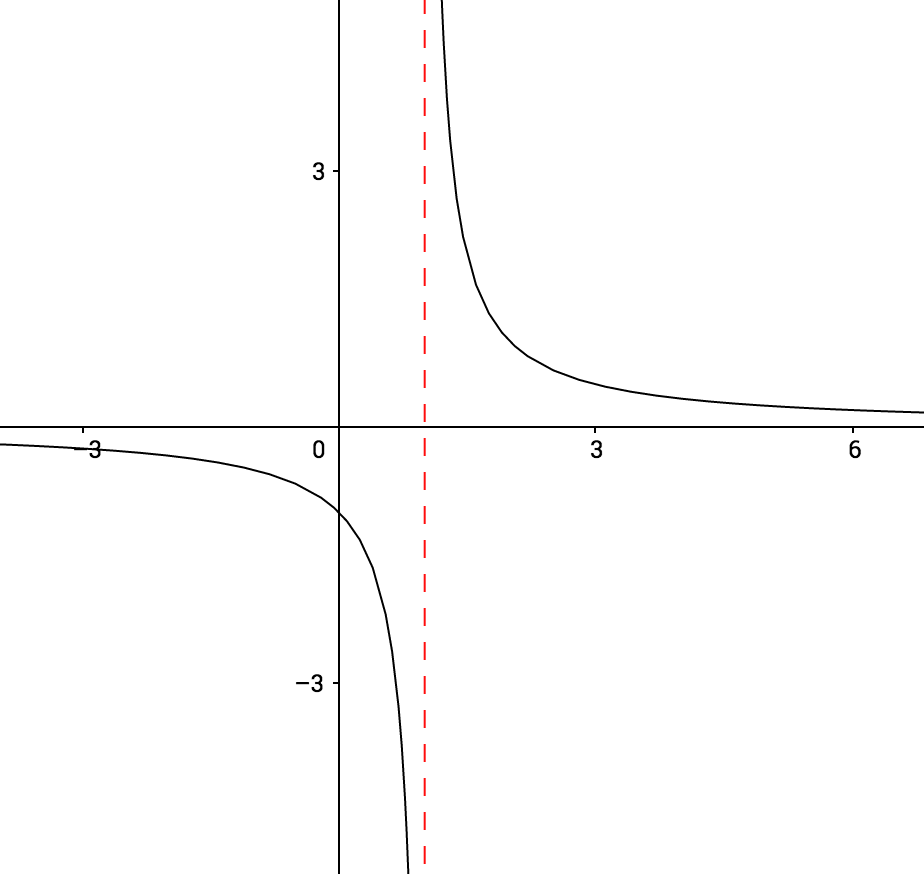
$$\text{Vertical asymptote } : $$
$$x=1$$
$$\text{Horizontal asymptote } : $$
$$y=0$$
$$y-\text{intercept } : $$
$$y=-1$$
$$x-\text{intercept } : $$
$$\text{none }$$
Rational Functions
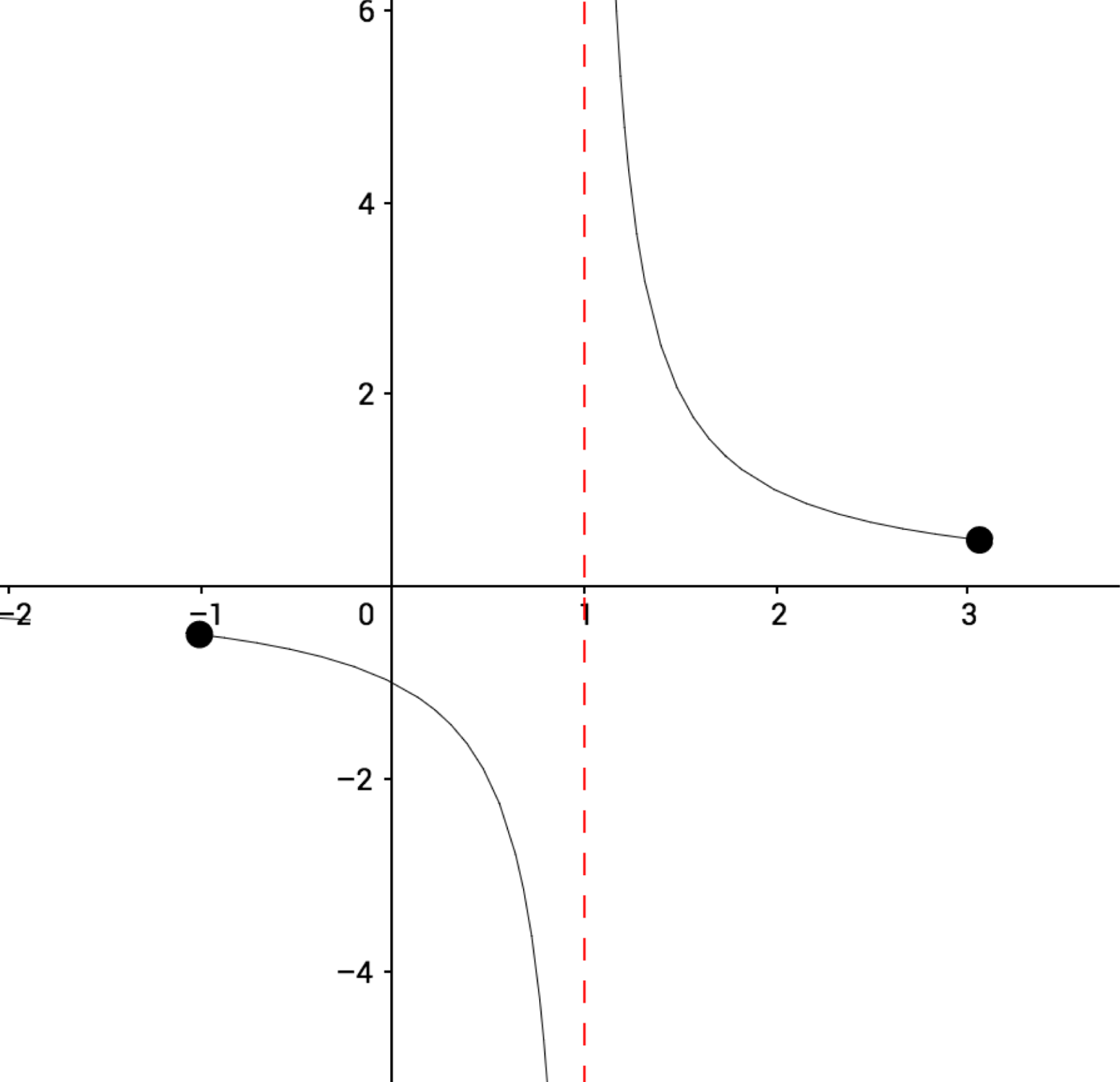
$$f(x) = \dfrac{1}{x-1} $$
$$ \text{set notation: } \ x\in [-1,3]$$
$$ -\{1\} $$
$$ \text{interval notation: } [-1,1) \cup (1, 3] $$
$$\text{domain of } f(x): $$
Continuity
A gateway to limits
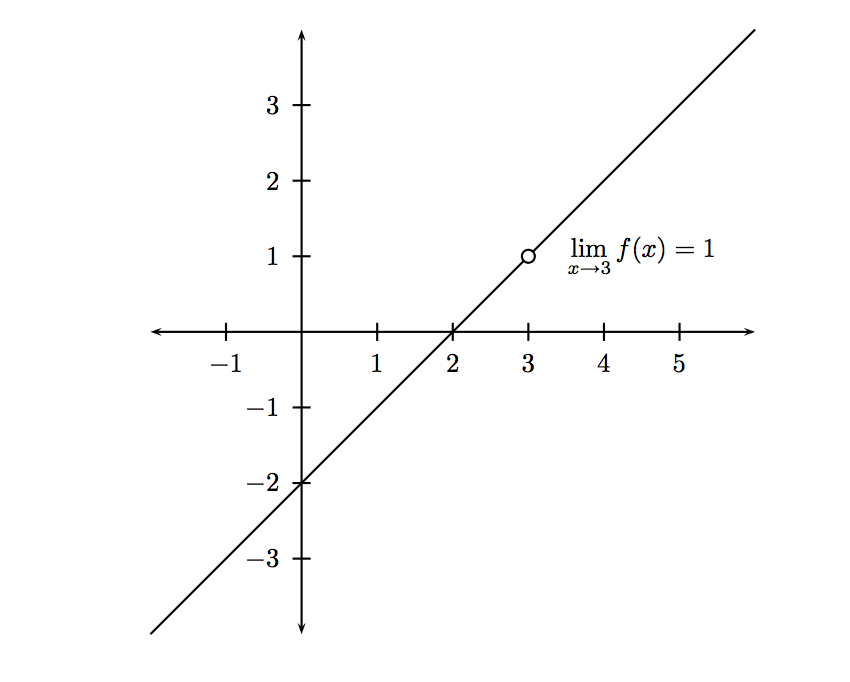
The equation for this function is
\(f(x)=x-2\)
except we have to specify that the function is discontinuous at \(x=3\)
\(f(x)=x-2 \ , x\ne 3\)
So what would be the domain of \(f(x)?\)
any value of \(x\) except \(x=3\) since when \(x\) is 3 there is a hole in the graph, so \(f(x)\) is not defined exactly when \(x=3\)
So we know \(f(3) \text{ is } \text{ undefined} \)
But where is \(f(x) \text{ approaching as } x \text{ gets closer to } 3? \)

\(f(3) = \text{ undefined}\)
$$ \lim _{x\to3} f(x) = 1$$
$$ f(x) = x-2, x\ne3 $$
Keep in mind that limits are the most important concept in both differential and integral Calculus!
Limits
Evaluating Limits:
Graphical Approach
Evaluating Limits Graphically

$$\lim_{x\to3^{-}} = $$
$$\lim_{x\to3^{+}} = $$
$$\lim_{x\to3} = $$
$$f(3) = $$
$$\lim_{x\to2^{+}} = $$
$$\lim_{x\to2^{-}} = $$
$$\lim_{x\to2} = $$
$$f(2) = $$
$$ \text{absolute maximum} = (1,3) $$
$$ \text{absolute minima} = \text{undefined}$$
$$ \text{local maximum} = (4,2) $$
\(2\)
\(1\)
\(\text{DNE}\)
\(3\)
\(1\)
\(1\)
\(1\)
\(\text{undefined}\)
\((1,3)\)
\((4,2)\)
$$ \text{increasing on: } (-\infty,1)\cup(2,3)\cup(3,4) $$
$$ \text{decreasing on: } (1, 2)\cup(4,\infty) $$
Try on your own until you get it 100% right

$$\lim_{x\to3^{-}} = $$
$$\lim_{x\to3^{+}} = $$
$$\lim_{x\to3} = $$
$$f(3) = $$
$$\lim_{x\to2^{+}} = $$
$$\lim_{x\to2^{-}} = $$
$$\lim_{x\to2} = $$
$$f(2) = $$
$$ \text{Intervals where }f(x) \text{ increases} = $$
$$ \text{Intervals where }f(x) \text{ decreases} = $$
$$ \text{absolute maxima} = $$
$$ \text{local maxima} = $$
$$x$$
Continuity and Direct Substitution
A limit is the point where the function would converge (or where both sides of the function would meet) as we make \(x\) get closer and closer to some value. To remember this, think of it as a question and ask yourself:
Where is \(f(x)\) approaching as \(x\) approaches \( a\)?
We don't care what the value of \(f(x)\) is at \( a\), we just care about the infinitesimal points before and after \(a\). The substitution rule is a method of finding limits, by simply substituting with \(x\) in the function \(f(x)\). This method can only be used if the function \(f(x)\) is continuous at \(a\).
You can look at it as evaluating any other function, except \(f(a)\) may not exist whereas \( \lim_{x\to a} f(x) \) may. However, \(f(x)\) must be continuous in order to accurately employ the substitution method. In other words, a function is continuous if :
\[\lim _{x \to a} f(x) = f(a)\]
\(\text{ Where is } f(x) \text{ approaching as } x \rightarrow 2 ? \)
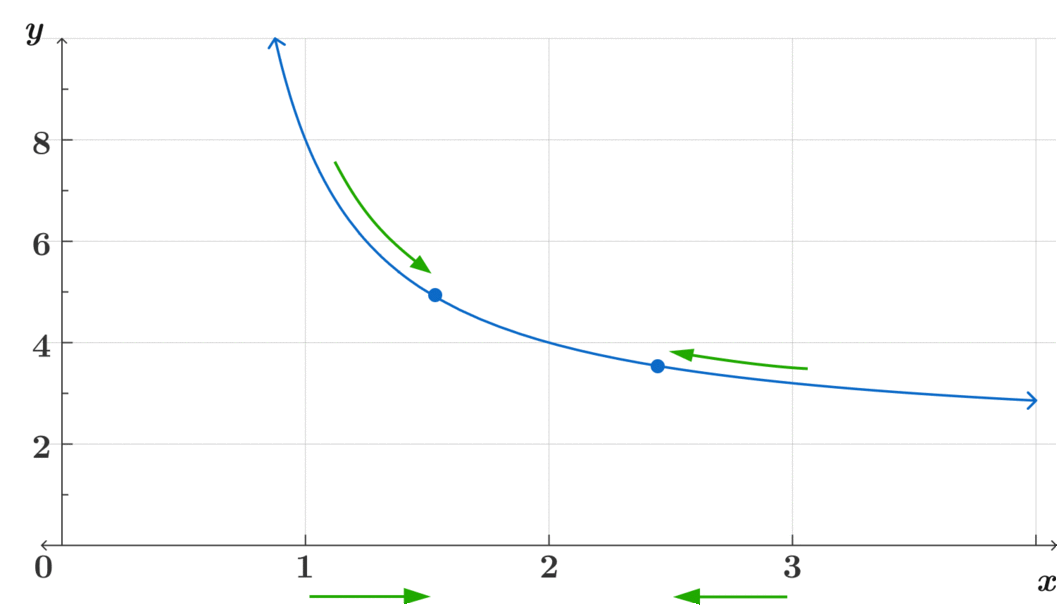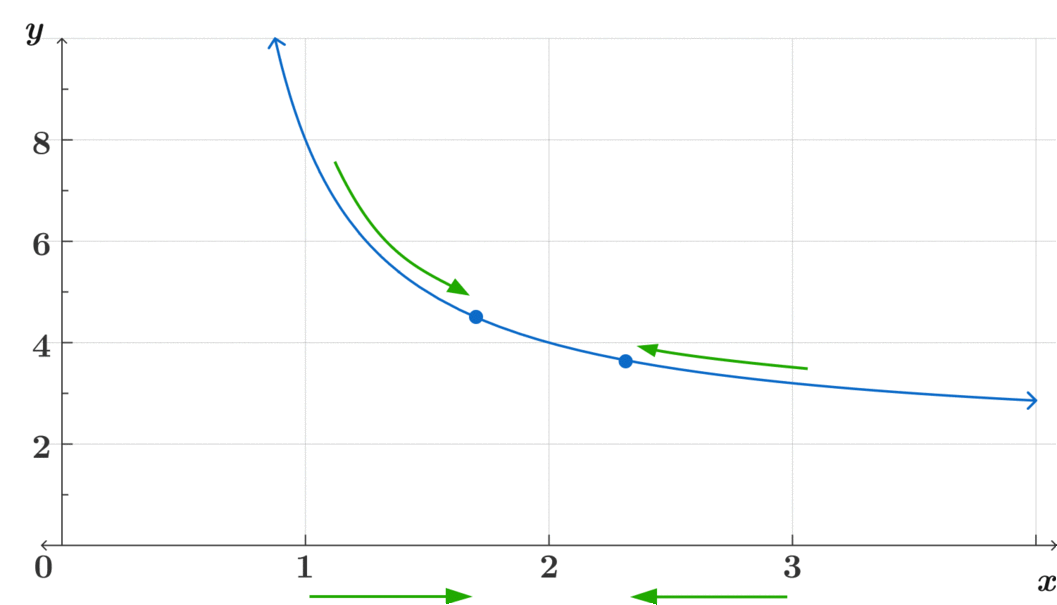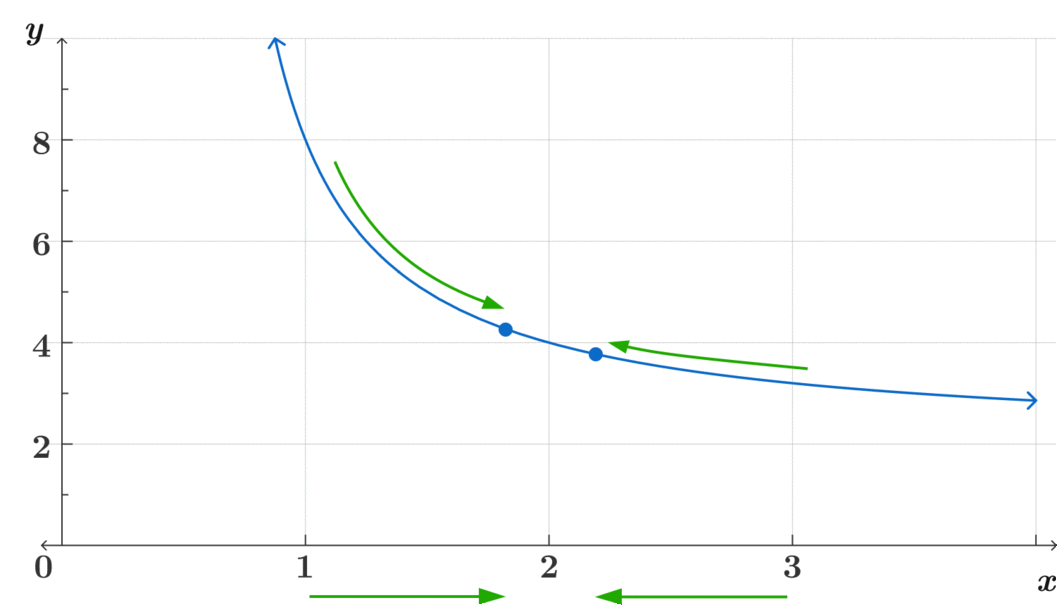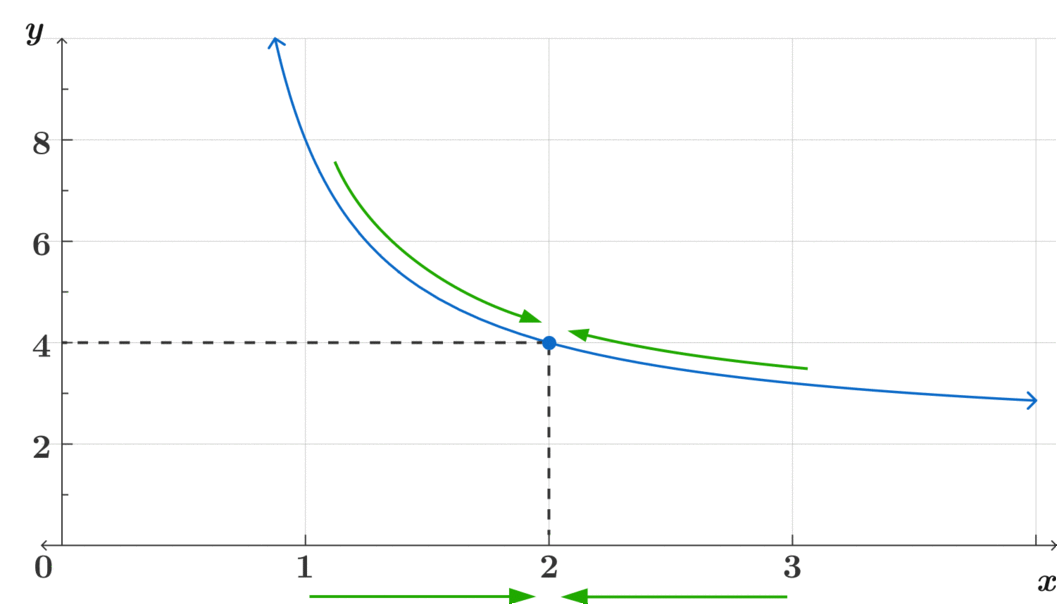
That is the key question to understanding limits through an intuitive way before learning more rigorous definitions.
\[\lim_{x\to2} f(x)= 4 \]
\[\text{Observe how} f(x) \text{ is continuous at } x=2 \]
Evaluating Limits Numerically
$$ \lim_{x\to0} \ x + 1$$
$$(0) + 1$$
$$= 1$$
$$ \lim_{x\to0} \ x + 1 = 1$$
$$ \leftarrow f(x) $$
$$ f(x) = x+1 $$
$$\leftarrow x$$
$$x \rightarrow $$
Since the function is continuous at \(x=0\) we substitute \(x\) \(\rightarrow\)\(0\)
Evaluating Limits Numerically

$$ \lim_{x\to0} \ f(x) = 1$$
$$ \leftarrow f(x) $$
$$ f(x) = x+1 $$
$$\leftarrow x$$
$$x \rightarrow $$
$$\text{Where is the function } f(x)$$
$$ \text{ approaching as } x \text{ approaches } 0? $$
$$ f(x) = x+1 $$

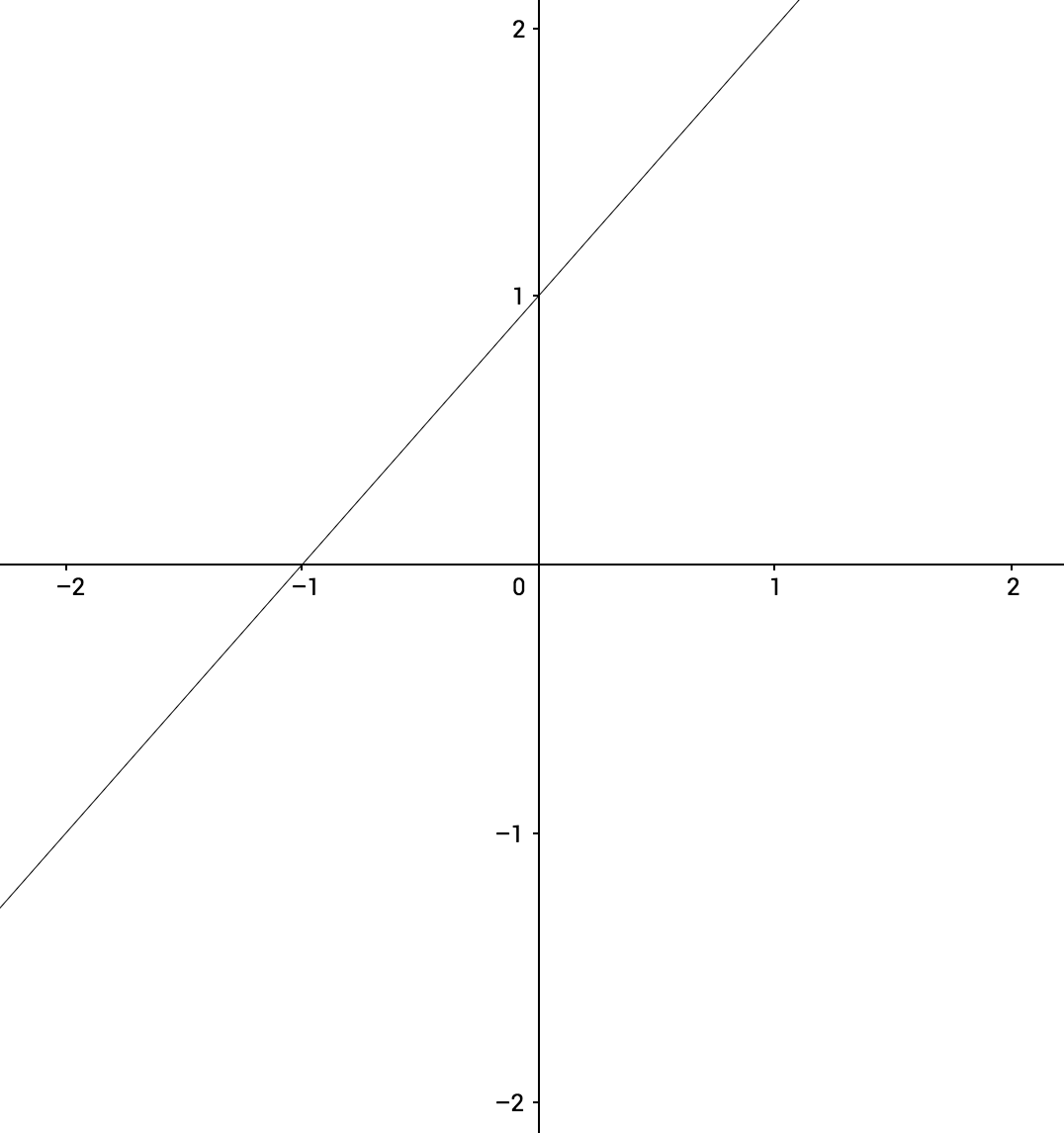
$$ \lim_{x\to1} \ x + 1$$
What happens as \(x\) approaches \(1\)?
$$(1) + 1 $$
$$= 2$$
$$ \lim_{x\to1} \ x + 1 = 2$$
By looking at the graph, what will be the \(\lim\) as \(x\to-1\)?
$$x \rightarrow 1$$
$$ \leftarrow x $$
Note that \(f(1)\) is defined:
\(f(1) = 2\)
$$\lim_{x\rightarrow a}f(x) = L $$
$$ \lim_{x\rightarrow a^{+}} = L =\lim_{x\rightarrow a^{-}} $$
$$ \lim_{x\to a^{+}} f(x) = L $$
$$ \lim_{x\to a^{-}} f(x) = L $$
i.e.
then we say "The limit of \(f(x)\) as \(x\) approaches \(a\) is \(L\)", and we write:
Existence of a limit
If
and
Limit of piecewise functions

$$\lim_{x\to0} $$
$$f(x) = x^2$$
$$f(x) = x+1$$
$$ f(x) = x^2$$
$$ f(x) = x+1$$
$$ \text{From negative infinity and up until } 0 $$
$$\text{just past 0 and unbound (up to infinity) } $$
The limit does not exist.
$$\text{so our function, made of two pieces, is: } $$
Limits of Piecewise Functions

$$\lim_{x\to0} f(x) = $$
$$\lim_{x\to0^{-}} f(x) = $$
$$\lim_{x\to0^{+}} f(x) = $$
$$\text{DNE}$$
$$ 0$$
$$ 1$$
$$\lim_{x\to0^{-}} \neq \lim _{x\to0^{+}}$$
$$\text{Since} $$
Evaluating Limits
$$\text{The }\dfrac{0}{0} \text{ case} $$
You might stumble find functions that will evaluate to be undefined upon direct substitution. This is known as the However, you should not automatically declare that the function is discontinuous. The 0/0 case is usually an indicator of further algebraic manipulation.
\[\dfrac{0}{0} \text{ case.}\]
We know that the result of any number \(a\) divided by \(0\) is not defined
Nonetheless, remember that we are interested in the values that are really close to \(a\), not \(a\) itself. So let's take a look at some examples to illustrate this situation.
Factoring
$$ \lim _{x\to3} \dfrac{x^2+x-12}{x-3}$$
$$\Rightarrow \dfrac{0}{0} \text{ case}$$
(we factor)
$$=\dfrac{(x+4)(x-3)}{(x-3)}$$
$$\Rightarrow (x+4)$$
$$ \lim _{x\to3} \dfrac{x^2+x-12}{x-3} = 7$$
$$\Rightarrow (3+4) =7 $$
(we substitute again)
$$ \lim _{x \to 4} \dfrac{x-4}{\sqrt{x} -2}$$
Rationalizing
$$\dfrac{x-4}{\sqrt{x} -2}$$
$$\dfrac{\sqrt{x}+2}{\sqrt{x} +2}$$
$$\Rightarrow \dfrac{(x-4)(\sqrt{x} +2)}{(x -4)}$$
$$= {\sqrt{x}+2}$$
$$\Rightarrow {\sqrt{4}+2 = 4}$$
$$ \lim _{x \to 4} \dfrac{x-4}{\sqrt{x} -2} = 4$$
•
$$\Rightarrow \dfrac{0}{0} \text{ case}$$
\( (\text{we substitute again)} \)
\( (\text{we rationalize)} \)
Computing Limits
Example 1
$$\lim_{x\to-2} 3x^2+5x-9 $$
Example 2
$$\Rightarrow 12-19= -7$$
$$\lim_{x\to0} {(x+e^{x})}^{-1}$$
$$= \lim_{x\to0}\dfrac{1}{(x+e^{x})}$$
$$= \lim_{x\to-2} 3(-2)^2+5(-2)-9 $$
$$= \lim_{x\to-2} 12-10-9 $$
$$\lim_{x\to-2} 3x^2+5x-9 = -7 $$
$$= \lim_{x\to0}\dfrac{1}{(0+e^{0})}$$
$$\Rightarrow \lim_{x\to0}\dfrac{1}{1}=1$$
$$\lim_{x\to0} {(x+e^{x})}^{-1} = 1$$
Example 3
$$\lim_{x\to2} \dfrac{x^3-4x}{x^2-4} $$
Example 4
$$=\lim_{x\to2} \dfrac{x(x^2-4)}{x^2-4} $$
$$=\lim_{x\to2} {x} =2$$
$$=\lim_{x\to2} {x} $$
$$\lim_{x\to6} \dfrac{x^2+x-42}{-12+2x} $$
$$= \lim_{x\to2} \dfrac{(x+7)(x-6)}{2(x-6)} $$
$$= \lim_{x\to2} \dfrac{(x+7)}{2} $$
$$ \Rightarrow \lim_{x\to2} \dfrac{(2+7)}{2} =\dfrac{9}{2} $$
$$\lim_{x\to6} \dfrac{x^2+x-42}{-12+2x} = \dfrac{9}{2} $$
$$\lim_{x\to2} \dfrac{x^3-4x}{x^2-4} = 2 $$
Example 5
$$\lim_{x\to-4} x^2+\sqrt{-4x} $$
Example 6
$$\Rightarrow 16+ 4= 20$$
$$\lim_{x\to0} {(x+1)^2}\cos{(\dfrac{x}{1-x})}$$
$$= \lim_{x\to-4} (-4)^2+\sqrt{-4(-4)} $$
$$= \lim_{x\to-4} 16+\sqrt{16} $$
$$\lim_{x\to-4} x^2+\sqrt{-4x} = 20$$
$$= \lim_{x\to0} {((0)+1)^2}\cos{(\dfrac{0}{1-0})}$$
$$\Rightarrow \lim_{x\to0} {(1)^2}\cos{(0)}$$
$$\Rightarrow \lim_{x\to0} {(1)}{(1)}=1$$
$$\lim_{x\to0} {(x+1)^2}\cos{(\dfrac{x}{1-x})}=1$$
Limits at Infinity
Limits Involving Infinity \(\infty\)
Before jumping into limits involving infinity, let's recall what indeterminate forms are and how to "evaluate" expressions that oscillate near these values. For instance, let's take a look at the expression \(\dfrac{1}{x}\).
Let's start with \(x=1\), plotting each time a greater value for \(x\)
\(\dfrac{1}{10000000}= 0.0000001\)
\(\dfrac{1}{1}=1\)
\(\dfrac{1}{100}=0.01\)
\(\dfrac{1}{10000}=0.00001\)
Do you see where the value of \(\dfrac{1}{x}\) is going? What would \(\dfrac{1}{x}\) be if \(x=1,000,000,000\)?
The expression \(\dfrac{1}{x}\) would get closer and closer to zero as \(x\) gets bigger and bigger. We can represent this mathematical behavior by assigning this huge number an infinite value: \(\infty\).
\(\text{ Any number divided by } \pm\infty \text{ approaches } 0\)
\[\lim_{x\to\infty}\dfrac{a}{x}=0 \]
\(\dfrac{a}{\infty}\ne0 \)
but!
'Intuitive' Forms:
\[ \dfrac{a}{\infty} = 0\]
\[ \dfrac{\infty}{a} = \infty\]
\[ a^{-1}=\dfrac{1}{a}\]
\[a^{\infty}=\infty\]
\[a^{-\infty}=\dfrac{1}{a^{\infty}}\]
\[a*\infty=\infty, a\ne 0\]
\[ \infty-\infty\]
\[a^{0}=1\]
\[\infty^{\infty}\]
\[\infty^{0}\]
\[0^{0}\]
\[1^{\infty}\]
\[\dfrac{0}{0}\]
\[0*\infty\]
Indeterminate Forms:
\[ \dfrac{a}{0^{+}} = \infty\]
\[ \dfrac{a}{0} = \text{und. }\]
\[ \dfrac{a}{0^{-}} = -\infty\]
Let's consider
What happens as \(x\to0\)
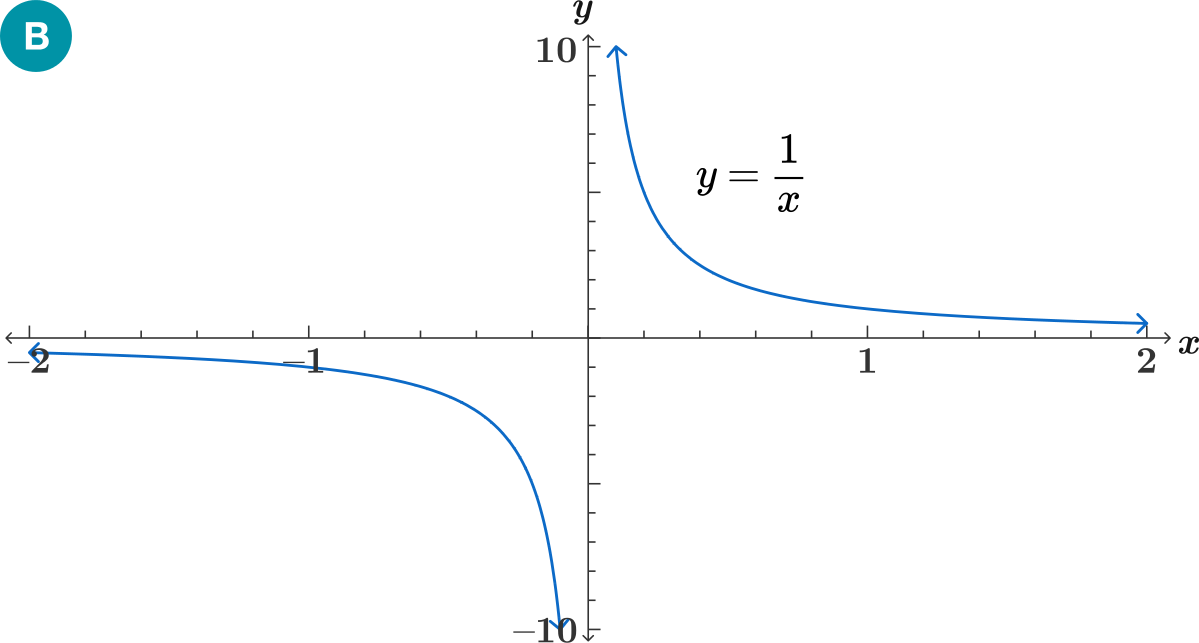
We know that
\( \lim _{x\to0} f(x) \text{ does not exist since}\)
But what happens when \(x\to-\infty\) ?
\[\lim_{x\to-\infty } \dfrac{ 1}{x}\]
\[\Rightarrow \dfrac{ 1}{(-\infty)}\]
\[\lim_{x\to-\infty } \dfrac{ 1}{x}=0\]
Similarly, when \(x\to\infty\)
\[\lim_{x\to\infty } \dfrac{ 1}{x} = \dfrac{1}{\infty} = 0\]
\[f(x) = \dfrac{1}{x} .\]
\(\lim _{x\to0^{-}} \ne \lim_{x\to0^{+}}\)
\[\lim_{x\to\infty } \dfrac{ 1}{x}=0\]
Analytical Approach
\[f(x) = \dfrac{9}{(x-3)^5}\]
\[\lim _{x\to3^{-}} f(x) = \]
\[\lim _{x\to3^{+}} f(x) = \]
\[\lim _{x\to3} f(x) = \]
Let's use our intuition first. If \(x \rightarrow 3^{-} \), then the denominator of \(f(x)\) will be negative, \(x - 3 < 0\), and progressively smaller as we get closer to 3 from the left. This looks like the form \(\dfrac{a}{0^{-}} \) , and even though the denominator will never be 0, we know
\[\lim _{x\to3^{-}} f(x) = \dfrac{9}{(2.99999-3)} = \dfrac{1}{0^{-}} = -\infty \]
\[\lim _{x\to3^{+}} f(x) = \dfrac{9}{(3.00001-3)} = \dfrac{1}{0^{+}} = \infty \]
\(\infty\)
\(-\infty\)
\(\text{DNE }\)
\(e^{\pm\infty}\)
\[\lim _{x\to\infty} e^x = \infty \]
Trick: \(e^{-\infty} = \dfrac{1}{e^{\infty}}\) and any number \(a^{\infty} = \infty\)
\[\lim _{x\to\infty} e^{-x} = 0 \]
\[\lim _{x\to-\infty} e^{x} = 0 \]
\[\lim _{x\to-\infty} e^{-x} = \infty \]
\[\lim_{x\to\infty} e^{-x}\]
\[\lim_{x\to-\infty} e^{x}=\]
\[\Rightarrow \frac{1}{e^{\infty}}\]
\[\lim_{x\to\infty} e^{-x}=0\]
\[e^{-\infty}\]
\[\Rightarrow \frac{1}{e^{\infty}}\]
\[\lim_{x\to -\infty} e^{x}=0\]
\[=\frac{1}{e^{x}}\]
\(3. \ f(x) = \dfrac{4x^4-3x^3+3x^2-3x+3}{2x^2+5x^3+2x^4} \)
\(2.\ f(x) = -(x^3-x)^{-2}\)
Find \(\lim_{x\to\infty}\) and \(\lim_{x\to-\infty}\) for the following functions:
\(1. \ f(x)= e^{2x^2-x+1}\)
\(4.\ f(x) =\dfrac{\sin{3x}}{x}\)
\[ \lim_{x\to0} f(x) =\dfrac{\sin{3x}}{x} \ ?\]
how about
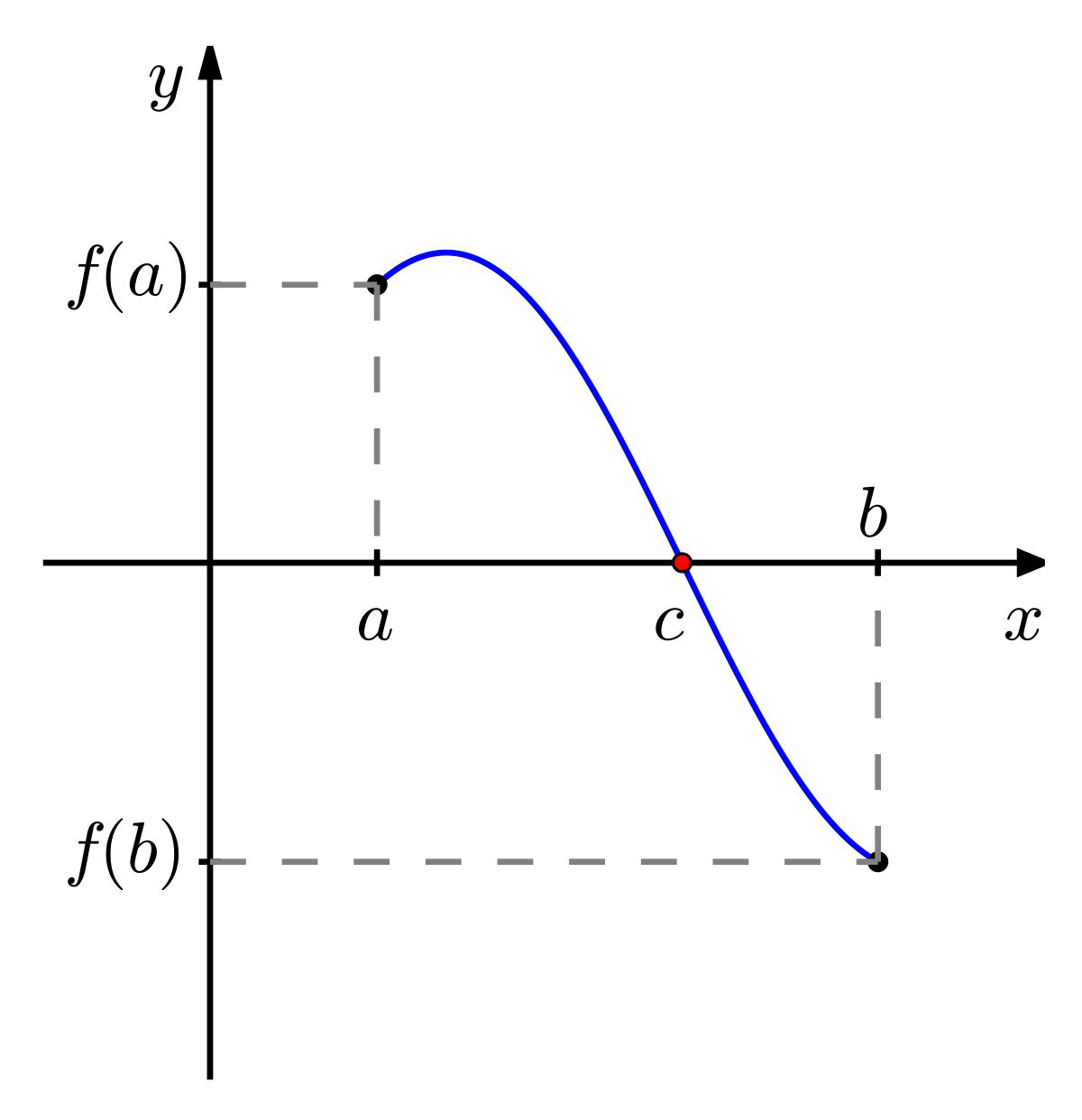
Intermediate Value Theorem
For any function \(f(x)\) that is continuous on \([a, b]\), and \(f(a)\) and \(f(b)\) exist, (at each end of the interval), then some value \(c\) must exist between \(a\) and \(b\) such that \(f(b)>f(c)>f(a)\)
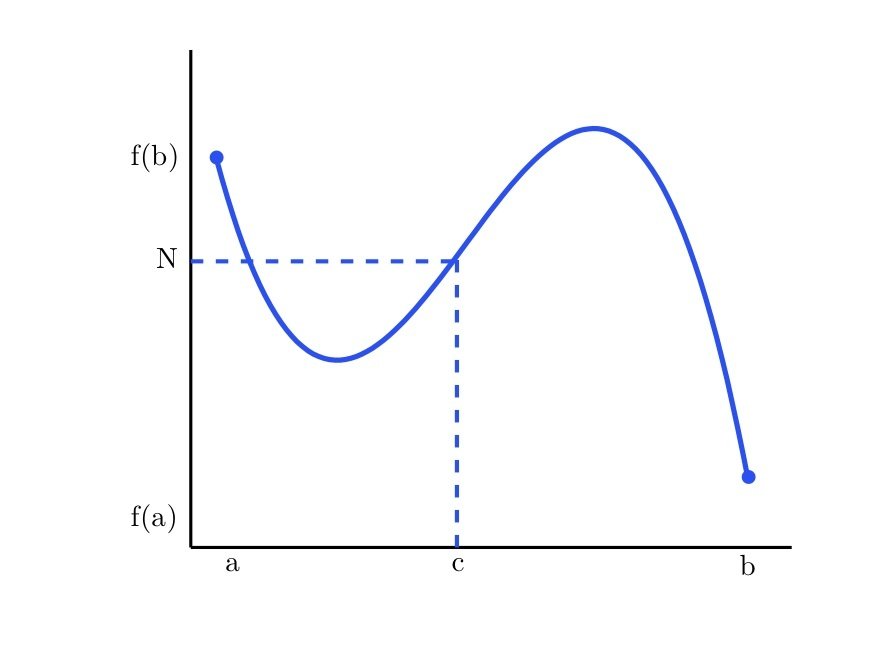
\(f(c)\)
\(f(a)\)
\(f(b)\)
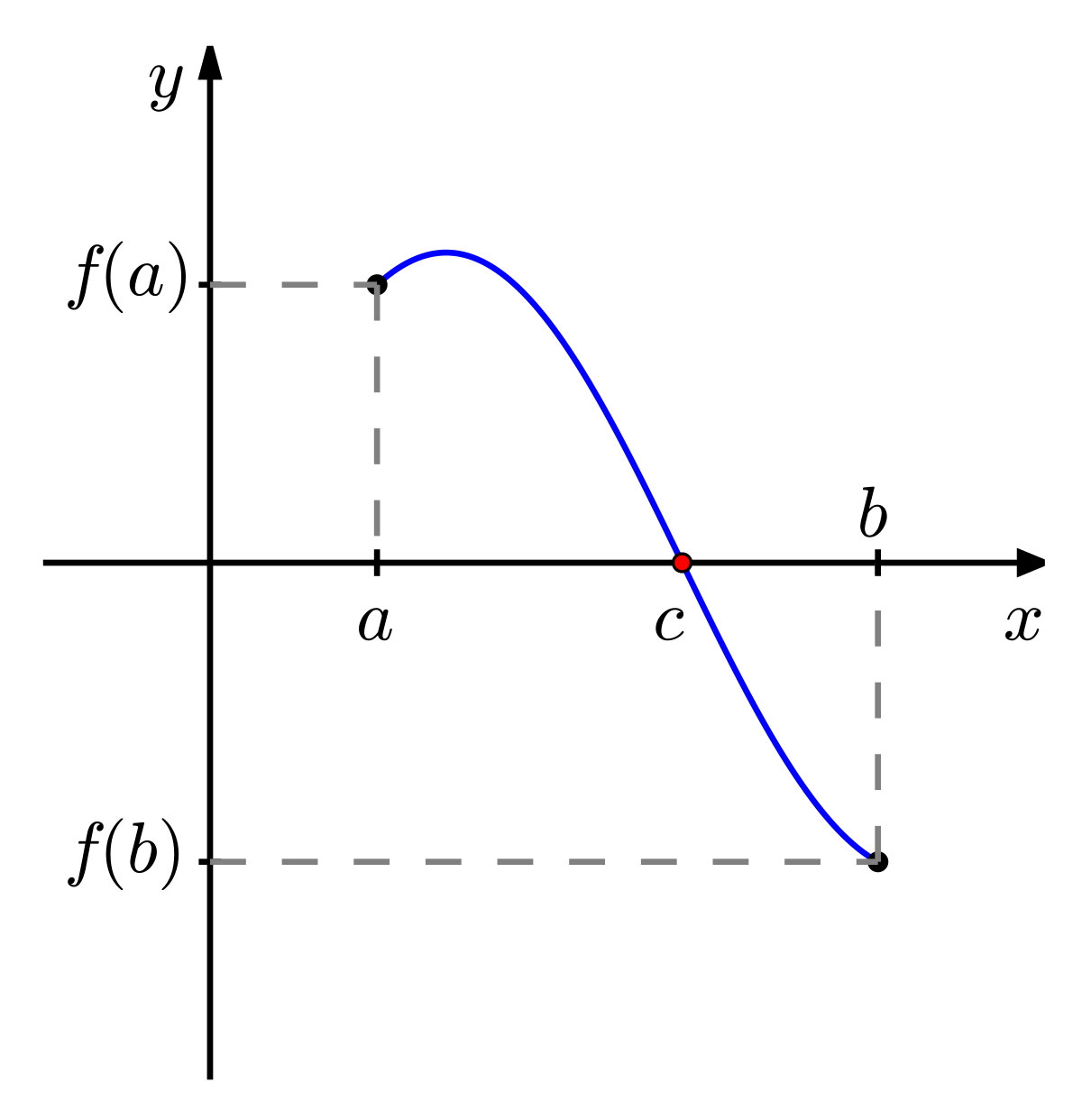
Intermediate Value Theorem
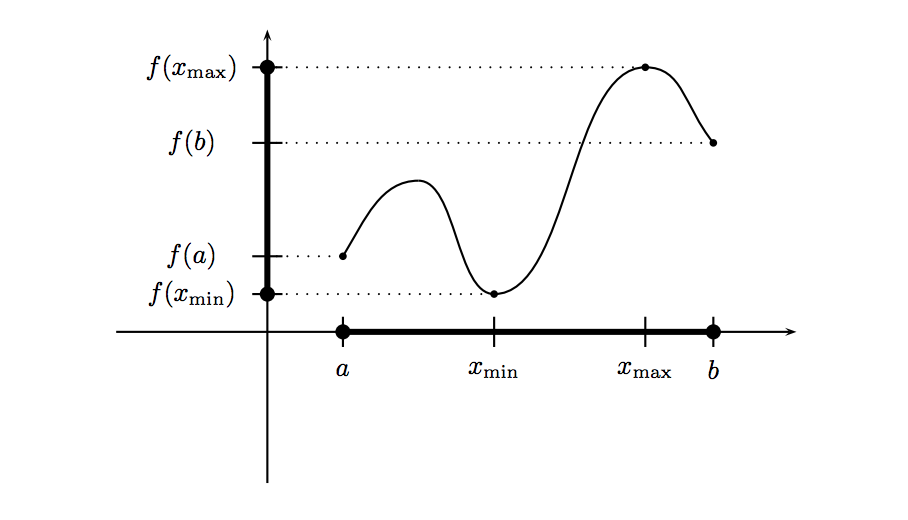
Domain:
$$[a,b]$$
Continuous on: $$[a,b]$$
$$\text{abs. minimum }$$
$$(x_{max}, f(x_{max}))$$
$$\text{abs. maximum }$$
Extreme Value Theorem
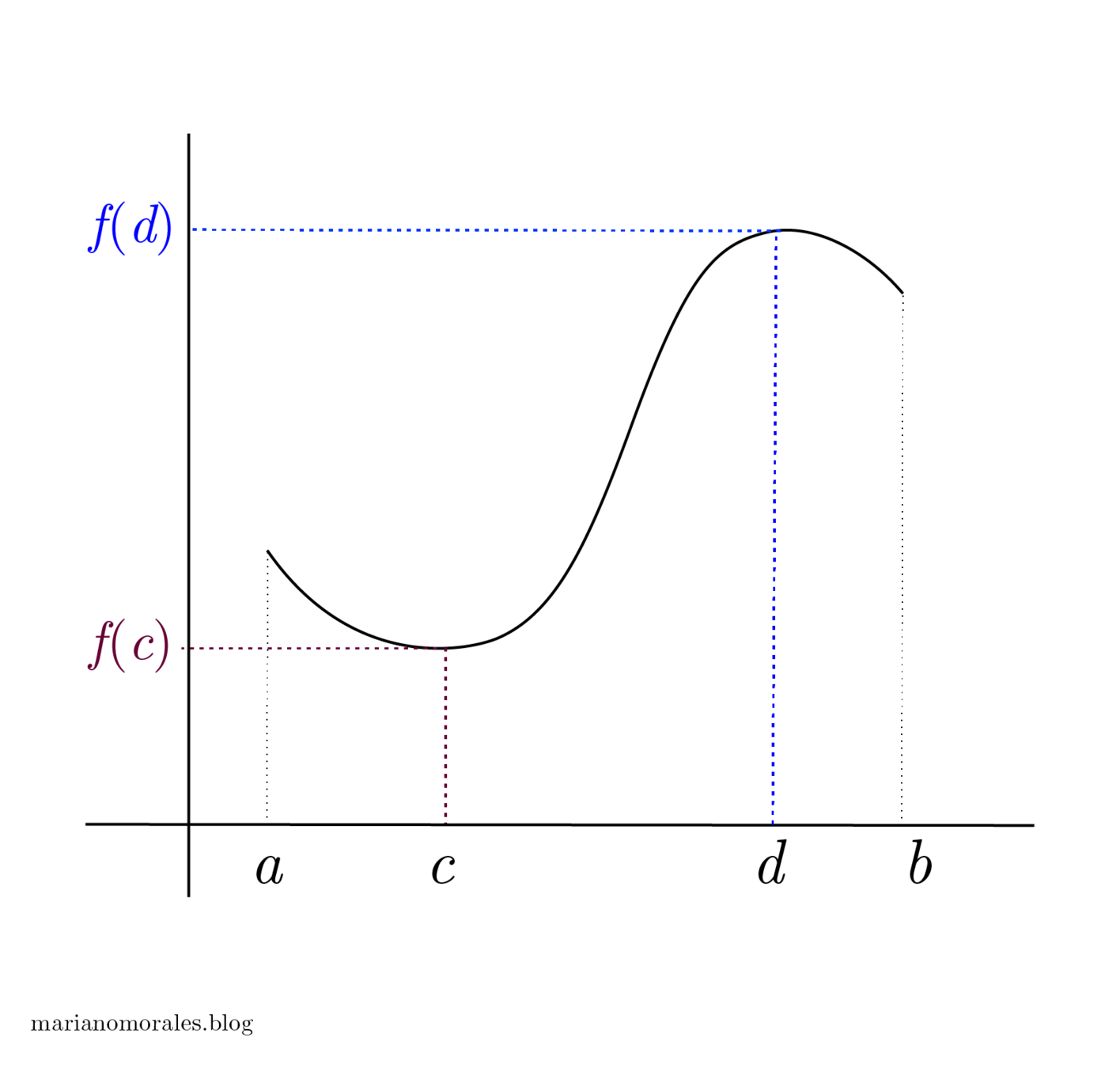
There is at least one point \(c\) in the interval \([a,b]\) such that \(f(c) \leq f(x) \) for all \(x\) in \([a,b]\) and there is at least one point \(d\) in the interval \([a,b]\) such that \(f(d) \geq f(x)\) for all \(x\) in \([a,b]\).
\(f(x)\)
Extreme Value Theorem
There is at least one point \(c\) in the interval \([a,b]\) such that \(f(c) \leq f(x) \) for all \(x\) in \([a,b]\) and there is at least one point \(d\) in the interval \([a,b]\) such that \(f(d) \geq f(x)\) for all \(x\) in \([a,b]\).
Consider the function \(f(x)\). Assume it is continuous on \([a,b]\). According to The Extreme Value Theorem, the function \(f\) will have a maximum value and also a minimum value within [a,b]

\(f(x)\)
Chain Rule
Differentiation
The Derivative
What the hell is a derivative, anyways?
are all the derivative of \(f(x)\):
\[f'(x) = \lim _{h\to0}\dfrac{f(x+h)-f(x)}{h}\]
The slope of the tangent line
\[m_{tan} = \dfrac{\Delta y}{\Delta x}\]
and the instantaneous rate of change
\[\lim_{\Delta x\to0}\dfrac{f(x+\Delta x) - f(x)}{\Delta x}\]
...yup, we are bound to have some fun! :)
Examples in Spanish
Differentiation Rules
(beta, in construction)
CRITICAL VALUES
We say that x=c is a critical point of the function f(x) if f(c)
exists and if either of the following are true:
f'(c)=0 OR f'(c) doesn't exist
FIND ALL CRITICAL VALUES
MINS AND MAXS
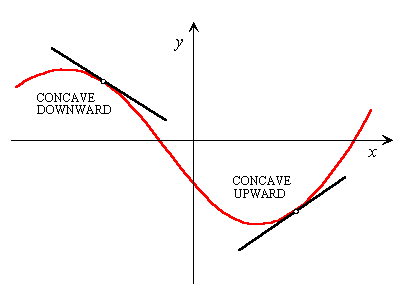
DEFINITION OF CONCAVITY
Let f(x) be a differentiable function on an open interval I.
The graph of f(x) is:
1. concave upward on I if f '(x) is increasing on the interval
2. concave downward on I if f '(x) is decreasing on the interval
CONCAVITY TEST
Let f(x) be a function whose second derivative exists on an open interval I.
1. If f ''(x) > 0 for all x in I , then the graph of f (x) is concave upward on I .
2. If f ''(x) < 0 for all x in I , then the graph of f (x) is concave downward on I .
INFLECTION POINT
If the graph of a continuous function possesses a tangent line at a point where its concavity changes from upward to downward (or vice versa), then the point is called a point of inflection.
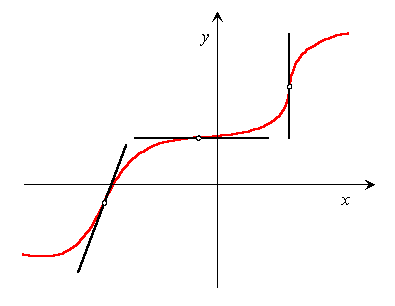
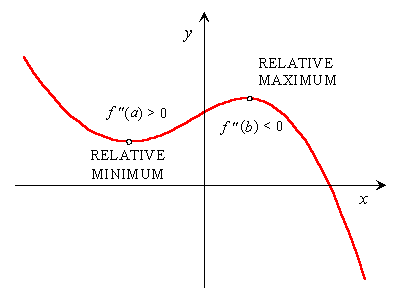
SECOND - DERIVATIVE TEST FOR RELATIVE EXTREMA
Let f ''(x) exists on some open interval containing c and f '(c) = 0.
1. If f ''(x) > 0, then f(c) is a relative minimum.
2. If f ''(x) < 0, then f(c) is a relative maximum.
3. If f ''(x) = 0, then nothing can be decided
Examaple 1
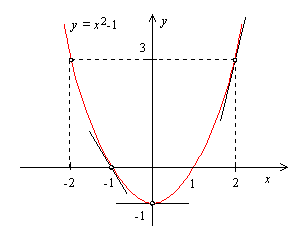
Function f(x) = x^2 - 1 is concave upward on the set of all real numbers because its second derivative
f''(x) = 2 is positive for all x.
Find any local extrema using the Second Derivative Test.
FIND THE CRITICAL VALUES
L'Hospital's Rule
It is possible to find the limit of some function whose limit evaluates to \( \dfrac{0}{0} \) or any indeterminate form. To reviews indeterminate forms, click here.
L'Hospital's Rule states that whenever
\[ \lim_{x \to a} \dfrac{f(x)}{g(x)} = \dfrac{0}{0} \]
we can find the limit by taking the derivative of the numerator and the denominator:
\[ \lim_{x \to a} \dfrac{f(x)}{g(x)} = \dfrac{f'(x)}{g'(x)} \]
The Integral
(beta, still in construction)
Position s(t)
Velocity v(t)
Acceleration a(t)
Initial Value Problems
The Area Problem
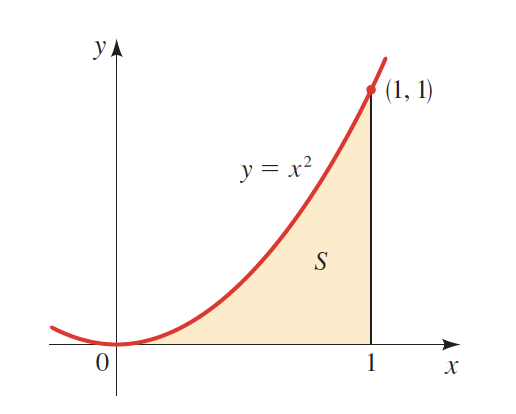
Imagine you want to find the area below the curve shown at the right.
Of course, there is no formula that can nearly be fixed for every area under every curve. However, we can approximate, to an infinitesimal point, the total area if we break it down into rectangles.
Let's see what I mean by this.
The Sum of the Areas
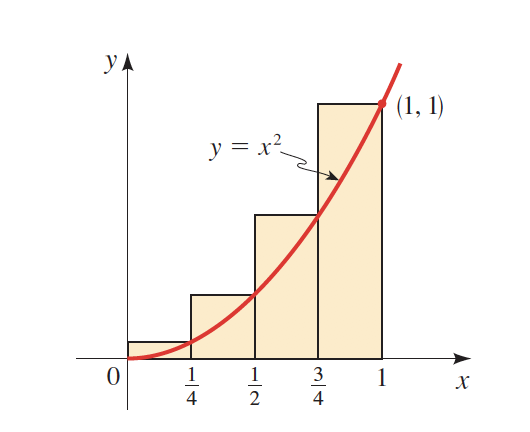

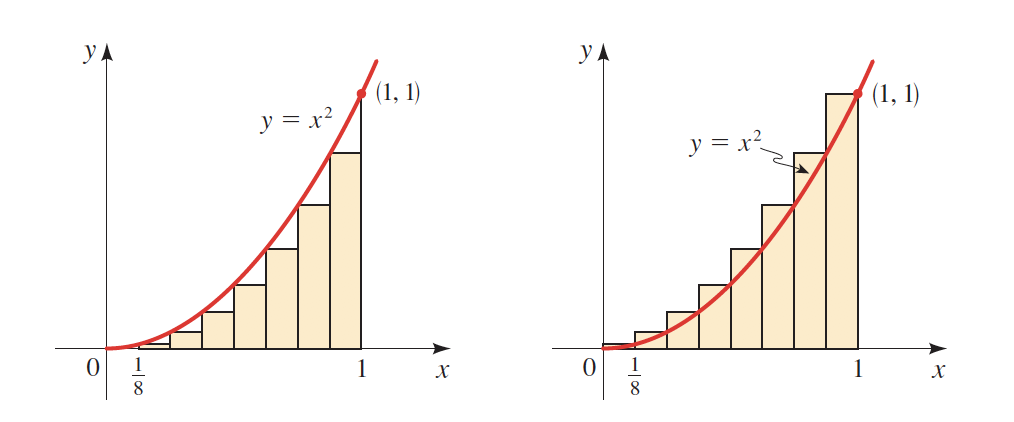

As observed in both curves, the more rectangles (\(n)\) we draw, the more accurate will be our result.
\(n=4\)
\(n=4\)
\(n=8\)
\(n=14\)
Limits in Integration
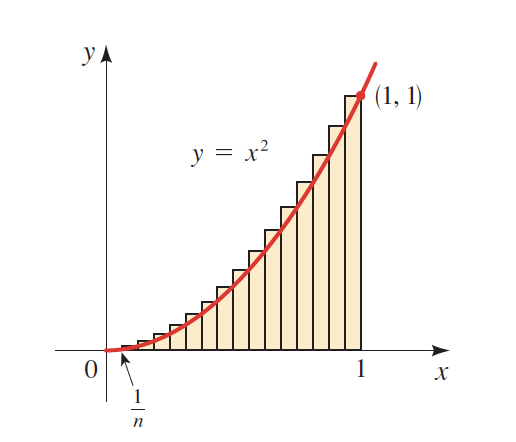
As we anticipated earlier, limits are also a fundamental concept behind integration. As a matter of fact, the limit is the most important concept in all calculus. Let's see the role that the limit plays in integration.
What is the base of each rectangle that is drawn between 0 and 1?
If we draw 5 rectangles \(n=5\), then the base of each rectangle will be \(\dfrac{1}{5}\) or \( \dfrac{1}{n}\). The height will vary, but the base will remain constant for every triangle.
Furthermore, we can find the area of each rectangle and add them up to come up with the exact area. The more rectangles we draw, the smaller will be the base of each triangle, but the more accurate we will get.
Solving the area problem
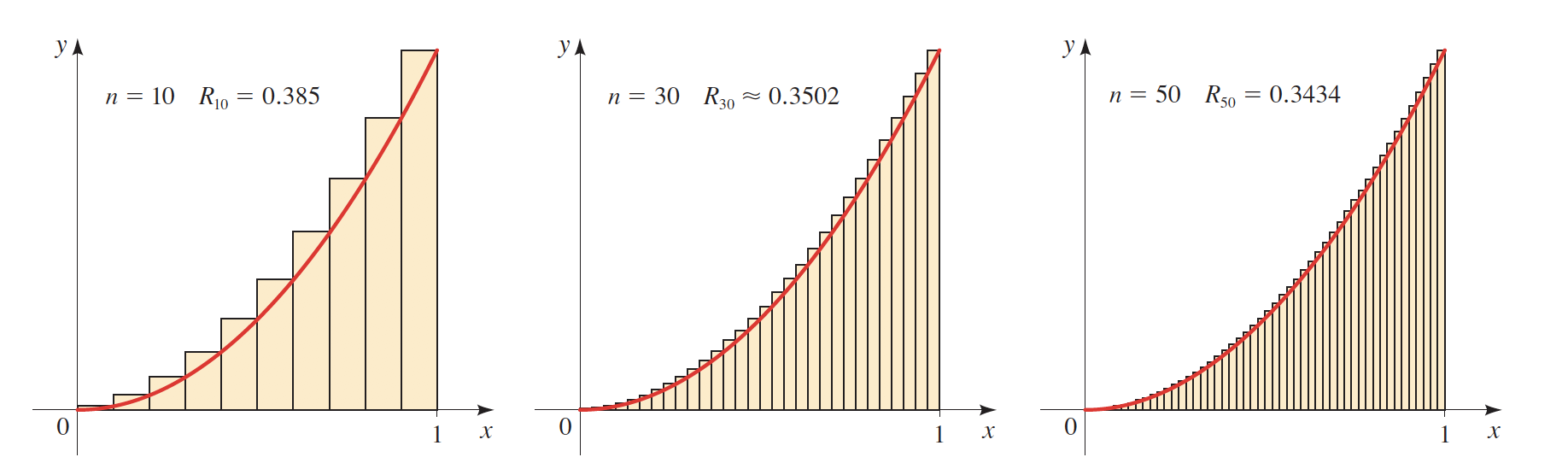
In the make as of July 31st, 2018
Title Text

Text
Techniques of Integration
Integration by Substitution
Integration by Parts
Intro to Calculus: Limits and Derivatives
By Mariano Morales
Intro to Calculus: Limits and Derivatives
Introduction to Limits - Class Notes
- 1,282


