covid trace
\( \frac{d}{dt} X(t_1, t) = \bar X(t) (1 - \frac{\bar X(t)}{N}) c \delta(t - t_1) - \frac{1}{\tau} X(t_1, t)\)
\(X(t_1,t) =\) number of people infected exactly at time \(t_1\) util time \(t\) (or later)
\( \bar X(t) = \int_{-\infty}^t X(t_1, t) dt_1= \) number of people infected at time \(t\)
\( \frac{d}{dt} X(t_1, t) = \bar X(t) (1 - \frac{\bar X(t)}{N}) c \delta(t - t_1) - \frac{1-p}{\tau} X(t_1, t) - R(t_1, t) X(t_1, t)\)
\( R(t_1, t) = R_+(t_1, t) + R_-(t_1,t)\) getting traced at time \(t\) if you were infected at time \(t_1\)
\( R_+(t_1, t) = \frac{p}{\tau} + cf \int_{t_1}^t dt' R_+(t', t) \) traced by you or your children
\( R_-(t_1, t) = f \int_{-\infty}^{t_1} dt' R(t', t) \frac{X(t', t_1)}{\bar X(t_1)} \) traced by your father
Exponential Solution for \(\bar X \ll N\)
\(X(t_1, t) = A e^{rt} x(t-t_1)\) with \(r\) and \(x\) such that:
\(\left\{ \begin{array}{l} x(t) = c\tau \exp( -(1-p + r\tau) t/\tau - \frac{p}{f c\tau} \frac{1}{1- f \int_0^\infty e^{f ct'} x(t') \frac{dt'}{\tau}} (e^{f ct}-1) ) \\ \int_0^\infty x(t) dt = \tau \end{array} \right. \)
\( \bar X(t) = A \tau \exp(rt)\)
\(fc \int_0^\infty e^{-Bfct - D (e^{fct}-1)} dt = e^D D^B \Gamma(-B, D) = A(B,D) \)
\(X(t_1, t) = A e^{rt} x(t-t_1)\) with \(r\) and \(x\) such that:
\(\left\{ \begin{array}{l} x(t) = c\tau \exp( -(1-p + r\tau) t/\tau - \frac{p}{f c\tau} \frac{1}{1- f \int_0^\infty e^{f ct'} x(t') \frac{dt'}{\tau}} (e^{f ct}-1) ) \\ \int_0^\infty x(t) dt = \tau \end{array} \right. \)
\( A(\frac{1-p+r\tau}{fc \tau}, \frac{p}{f c\tau} \frac{1}{1- f I}) = f \)
\( fI = A(\frac{1-p+r\tau}{fc \tau} - 1, \frac{p}{f c\tau} \frac{1}{1- f I}) \)
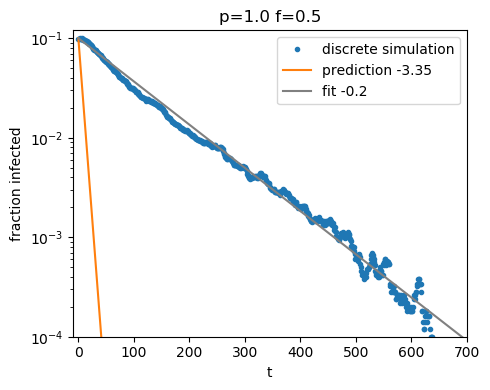
resolution
\( \frac{d}{dt} X(t_1, t) = (\bar X(t) (1-\bar X(t) / N) c + c') \delta(t - t_1) - \frac{1-p}{\tau} X(t_1, t) - R(t_1, t) X(t_1, t)\)
\( R(t_1, t) = R_+(t_1, t) + R_-(t_1,t)\)
\( R_+(t_1, t) = \frac{p}{\tau} + cf \int_{t_1}^t dt' R_+(t', t) \)
\( R_-(t_1, t) = f \int_{-\infty}^{t_1} dt' R(t', t) \frac{X(t', t_1)}{\bar X(t_1)} \)
first step \(X(t_1, t) = A e^{rt/\tau} x(t-t_1)\)
\( \bar X(t) = A e^{rt/\tau} \int_0^\infty x(t') dt' \)
\( \frac{r}{\tau} x(t-t_1) + \dot x(t-t_1) = (c \int_0^\infty x(t')dt' (1-\bar X(t) / N) + \frac{c'}{A} e^{-r t/\tau} ) \delta(t - t_1) - \frac{1-p}{\tau} x(t-t_1) - R(t_1, t) x(t-t_1)\)
\( R(t_1, t) = R_+(t_1, t) + R_-(t_1,t)\)
\( R_+(t_1, t) = \frac{p}{\tau} + cf \int_{t_1}^t dt' R_+(t', t) \)
\( R_-(t_1, t) = f \int_{0}^{\infty} dt' R(t_1-t', t) \frac{x(t')}{\int_0^\infty x(\tilde t) d\tilde t } \)
Second step
\( R(t_1, t) = R_+(t_1, t) + R_-(t_1,t)\)
\( R_+(t - t_1) = \frac{p}{\tau} e^{cf (t-t_1)} \)
\( R_-(u) = B e^{cfu} = f \int_{0}^{\infty} dt' ( \frac{p}{\tau} + B) e^{cf (u+t')} \frac{x(t')}{\int_0^\infty x(\tilde t) d\tilde t } \)
\(\Longrightarrow B \int_0^\infty x(t) dt = f ( \frac{p}{\tau} + B) \int_{0}^{\infty} e^{cf t} x(t) dt \Longrightarrow R(t_1, t) = \frac{p}{\tau} \frac{1}{1- f \frac{\int e^{cft} x(t) dt}{\int x(t) dt}} e^{cf(t-t_1)} \)
last setp
\( \dot x(u) = (c \int_0^\infty x(t)dt (1-\bar X(t) / N) + \frac{c'}{A} e^{-r t/\tau} ) \delta(u) - \left(\frac{1-p+r}{\tau} + \frac{p}{\tau} \frac{1}{1- f \frac{\int e^{cft} x(t) dt}{\int x(t) dt}} e^{cfu} \right) x(u)\)
\( x(u) = (c \int x(t)dt (1-\frac{A}{N} e^{rt/\tau} \int x(t)dt)+ \frac{c'}{A} e^{-rt/\tau}) \exp( -\frac{1-p+r}{\tau}u - \frac{p}{cf\tau} \frac{1}{1- f \frac{\int e^{cft} x(t) dt}{\int x(t) dt}} (e^{cfu} - 1)) \)
if \(c' \neq 0 \Rightarrow r=0 \)
\( x(u) = (c \int x(t)dt (1-\frac{A}{N} \int x(t)dt) + \frac{c'}{A}) \exp( -\frac{1-p}{\tau}u - \frac{p}{cf\tau} \frac{1}{1- f \frac{\int e^{cft} x(t) dt}{\int x(t) dt}} (e^{cfu} - 1)) \)
\(A\) can be fixed by fixing the integral of \(x\)
\( \left\{ \begin{array}{l} x(u) = (c (1 - \frac{A}{N}) + \frac{c'}{A}) \exp( -\frac{1-p}{\tau}u - \frac{p}{cf\tau} \frac{1}{1- f \int e^{cft} x(t) dt} (e^{cfu} - 1)) \\ \int x(t) dt = 1\end{array}\right. \)
Old slides
Problem
\( \frac{d}{dt} X(t_1, t) = -\frac{1-p}{\tau} X(t_1, t) + \bar X(t) (1 - \frac{\bar X(t)}{N}) c \delta(t - t_1) - R(t_1, t) X(t_1, t)\)
\( \bar X(t) = \int_{-\infty}^t X(t_1, t) dt_1\)
\( R(t_1, t) = R_+(t_1, t) + R_-(t_1,t)\)
\( R_+(t_1, t) = \frac{p}{\tau} + cf \int_{t_1}^t dt' R_+(t', t) \quad \Rightarrow R_+(t_1, t) = \frac{p}{\tau} e^{cf (t-t_1)} \)
\( R_-(t_1, t) = f \int_{-\infty}^{t_1} dt' R(t', t) \frac{X(t', t_1)}{\bar X(t_1)} \)
Exponential Solution for \(N\to\infty\)
\(X(t_1, t) = A e^{rt} x(t-t_1)\) with \(r\) and \(x\) such that:
\(x(t) = c\tau \exp( -(1-p + r\tau) t/\tau - \frac{p}{f c\tau} \frac{1}{1- f \int_0^\infty e^{f ct'} x(t') \frac{dt'}{\tau}} (e^{f ct}-1) )\)
and \( \int_0^\infty x(t) dt = \tau \)
\( \frac{d}{du} X(u) = -\frac{1-p}{\tau} X(u) + \bar X (1 - \frac{\bar X}{N}) c \delta(u) - R(u) X(u)\)
\( \frac{d}{du} \ln X(u) = -\frac{1-p}{\tau} - R(u) \)
for u > 0
\( X(u) = \exp( -\frac{1-p}{\tau}u - \int^u R(u')du' ) \)
\( R(u) = \frac{p}{\tau} e^{cfu} + R_-(u) \)
\( \Rightarrow X(u) = \exp( -\frac{1-p}{\tau}u - \frac{p}{cf\tau} (e^{cfu}-1) - \int^u R_-(u')du' ) \)
for all u
\( X(u) = X(0) \exp( -\frac{1-p}{\tau}u - \frac{p}{cf\tau} (e^{cfu}-1) - \int_0^u R_-(u')du' ) \)
using \( X(0) = \bar X (1 - \frac{\bar X}{N}) c \)
\( R_-(u) = f \int_{u}^{\infty} du' R(u') \frac{X(u'-u)}{\bar X} \)
solutions de la forme exponentielle
\( X(t_1, t) = e^{r t_1} h(t - t_1) = e^{r t} g(t - t_1) \quad \Rightarrow e^{-ru} h(u) = g(u) \)
\( R(t_1, t) = R(t - t_1) \)
\( \bar X(t) = \int_{-\infty}^t e^{r t} g(t-t_1) dt_1 = e^{rt} \int_0^\infty g(u) du = e^{rt} \bar g \)
\( h'(u) = -\frac{1-p}{\tau} h(u) - R(u) h(u) + \delta(u) e^{r u} \bar g c\)
\( R(u) = R_+(u) + R_-(u)\)
\( R_+(u) = \frac{p}{\tau} e^{cf u} \)
\( R_-(u) = \frac{f}{\bar g} \int_{u}^{\infty} du' R(u') e^{-r (u' - u)} h(u' - u) = \frac{f}{\bar g} \int_{u}^{\infty} du' R(u') g(u'-u) \)
\(\Rightarrow \)
\( g'(u) = -r g(u) -\frac{1-p}{\tau} g(u) - R_-(u) g(u) - \frac{p}{\tau} e^{cf u} g(u) + \delta(u) \bar g c\)
\( \Rightarrow g(u) = g(0) \exp(-r u -\frac{1-p}{\tau} u - \int_0^u R_-(u')du' - \frac{p}{cf \tau} (e^{cf u} - 1)) \)
\( g(0) = \bar g c \)
\( R_-(u) = \frac{f}{\bar g} \int_{u}^{\infty} du' R(u') g(u'-u) \)
original
\( g(u) = g(0) \exp(-r u -\frac{1-p}{\tau} u - \int_0^u R_-(u')du' - \frac{p}{cf \tau} (e^{cf u} - 1)) \)
\( g(0) = \bar g c \) with \( \bar g = \int_0^\infty g(u) du \)
\( R_-(u) = \frac{f}{\bar g} \int_{u}^{\infty} du' (\frac{p}{\tau} e^{cf u'} + R_-(u')) g(u'-u) \)
adimention
dict
\( u = \tau \tilde u\)
\( r\tau = \tilde r \) \( g(\tau \tilde u) = \tilde g(\tilde u) \)
\( \tau c = \tilde c \) \( \tau R_-(\tau \tilde u) = m(\tilde u) \)
adim
\( \tilde g(\tilde u) = \tilde g(0) \exp(- (1-p+\tilde r) \tilde u - \int_0^{\tilde u} m(\tilde u') d\tilde u' - \frac{p}{\tilde c f} (e^{\tilde c f \tilde u} - 1)) \)
\( \tilde g(0) = \tilde c \bar g / \tau \) with \( \bar g / \tau = \int_0^\infty \tilde g(\tilde u) d\tilde u \)
\( m(\tilde u) = \frac{f}{\bar g / \tau} \int_{\tilde u}^{\infty} d\tilde u' (p e^{\tilde c f \tilde u'} + m(\tilde u')) \; \tilde g(\tilde u'- \tilde u) \)
\( X(t_1, t) = e^{r t} \tilde g(\frac{t - t_1}{\tau}) \)
\(1 + \tilde r = \tilde c \)
Si \(p=0\)
\( \tilde g(\tilde u) = \tilde c \tilde g \exp(- (1+\tilde r) \tilde u - p (\frac{e^{\tilde c f \tilde u} - 1}{\tilde c f (1 - f \frac{I}{\tilde g})} - \tilde u)) \)
with
- \( \tilde g = \int_0^\infty \tilde g(\tilde u) d\tilde u \)
- \( I = \int_{0}^{\infty} e^{\tilde c f \tilde u} \; \tilde g(\tilde u) d\tilde u \)
covid
By Mario Geiger
covid
- 982



