\(U \subset \mathbb{R}^d\)
\(\xi: U \rightarrow \mathbb{R}^d\)
\(x: U \rightarrow \mathbb{R}\)
\([\tau x](s) = x(s')\) where \(s' + \xi(s') = s\)
\(s\mapsto s + \xi(s)\) is bijective and continuous
\(\forall s\in D, u\neq0\in \mathbb{R}^d \quad \|u + (u\cdot\nabla) \xi(s) \| \neq 0\)
\(s\)
\(u\)
\(s+\xi(s)\)
\(u + (u\cdot \nabla) \xi(s)\)
\(u\cdot(u + (u\cdot\nabla) \xi(s) ) > 0\)
\( \frac12 \left( \sqrt{\|\nabla \xi\|^2 - 2 \det(\nabla \xi)} - \mathrm{Tr}(\nabla\xi) \right) < 1 \)
\(\|A\|_\infty \equiv \sup\{\|Au\|: u \text{ unitary} \}\)
\(\|A\|_\infty = \|USV\|_\infty = \|S\|_\infty = \max_i S_i\)
\( \| A \|_\infty^2 = \frac12\left( \|A\|^2 + \sqrt{\|A\|^4-4\det(A)^2} \right)\)
\(\| \nabla \xi(s) \|_\infty < 1\)
\(u\)
\(\|(u\cdot\nabla) \xi(s)\|_\infty < 1\)
\(\frac12\left( \|\nabla \xi\|^2 + \sqrt{\|\nabla \xi\|^4-4\det(\nabla \xi)^2} \right) < 1\)
\(\|u + (u\cdot\nabla) \xi(s) \| \neq 0\)
\((u\cdot\nabla) \xi(s) \neq -u\)
\(u + (u\cdot\nabla) \xi(s)\)
\((u\cdot\nabla) \xi(s)\)
\(u\cdot(u + (u\cdot\nabla) \xi(s) ) > 0 \quad \forall u\)
\(\Leftrightarrow\)
\(\frac12 \left(\sqrt{(\partial_x \xi_x - \partial_y \xi_y)^2 + (\partial_x \xi_y + \partial_y \xi_x)^2} - \partial_x \xi_x - \partial_y \xi_y\right) < 1\)
\(\Leftrightarrow\)
\( \frac12 \left( \sqrt{\|\nabla \xi\|^2 - 2 \det(\nabla \xi)} - \mathrm{Tr}(\nabla\xi) \right) < 1 \)
\(\max_s \frac12 \left( \sqrt{\|\nabla \xi\|^2 - 2 \det(\nabla \xi)} - \mathrm{Tr}(\nabla\xi) \right) \approx 2.5 \frac{c^{1.1}}{n} \sqrt{T}\)
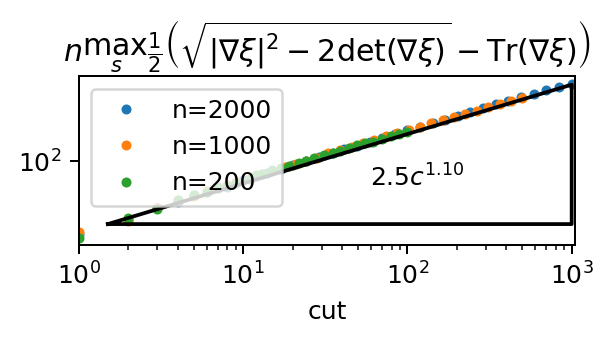
overhang
By Mario Geiger
overhang
- 835



