Mateo Sanabria Ardila
ISIS1105: Diseño y análisis de algoritmos

Dividir y Conquistar

Dividir y Conquistar

Se rompe el problema en subproblemas que son idénticos al original pero de menor tamaño:  
  1. Se soluciona los subproblemas
  2. Se combinan las soluciones, para dar solución al problema original

Dividir y Conquistar

  • Búsqueda Binaria
  • Merge Sort
  • Quicksort
  • Problema: Cantidad de años
  • Problema: Alcanzar el Valhalla
  • Pares de puntos mas cercanos

  • Problema del máximo subarreglo
  • Algoritmo de Strassen (multiplicación de matrices)

Ventajas

  • Se adapta naturalmente a la computación paralela
  • Usualmente hacen uso eficiente de memoria (DEPENDE!)

Desventajas

  • Recursión (Stack overflow) 
  • Subproblemas repetidos

Complejidad D&C

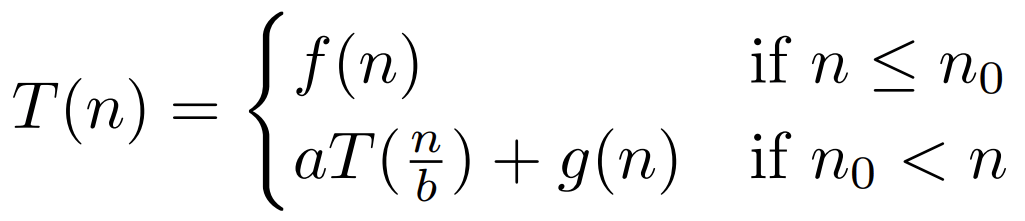
Donde a es el número de subproblemas y 1/b es la fracción de los datos a procesar en cada caso recursivo

Dividir y conquistar: Merge Sort

Merge Sort

  1. Divide: Divide los n-elementos del arreglo en dos subarreglos de tamaño n/2 cada uno
  2. Conquista: Ordena cada una de los subarreglos usado Merge-Sort  
  3. Combina: Une (Merge) dos subarreglos ordenados para entregar la respuesta ordenada
El caso Base se da cuando se alcanza un arreglo de longitud 1
def merge_sort(array):
    if len(array)<2:
        return array
    else:
        midpoint=len(array)//2
        left,right = array[:midpoint], array[midpoint:]
        left,right = merge_sort(left), merge_sort(right)
        return merge(left,right)

Divide y conquista:

def merge(left,right):
    result=[]
    l_pointer = r_pointer = 0
    while l_pointer < len(left) and r_pointer < len(right):
        if left[l_pointer] < right[r_pointer]:
            result.append(left[l_pointer])
            l_pointer+=1
        else:
            result.append(right[r_pointer])
            r_pointer+=1
    result.extend(left[l_pointer:])
    result.extend(right[r_pointer:])
    return result

Combinar (merge): 

def merge_sort(array):
    if len(array)<2: # <- ?
        return array # <- ?
    else:
        midpoint=len(array)//2 <- #?
        left,right = array[:midpoint], array[midpoint:] # <- ?
        left,right = merge_sort(left), merge_sort(right) # <- ?
        return merge(left,right) # <- ?

Cual es la complejidad del algoritmo?

Cual es la complejidad del algoritmo?
  1. Divide: Toma tiempo constate, k.
  2. Conquista: El problema de divide en dos subproblemas de tamaño n/2, se tiene 2R(n/2).  
  3. Combina: Es lineal, luego el costo es, n.
R(n) = \left\{ \begin{array}{ll} k & \quad n = 1 \\ 2R(n/2) + n & \quad x > 1 \end{array} \right.

Dividir y conquistar: Quick Sort

QUICK Sort

  1. Divide: Dividir el arreglo inicial A[0:N] en dos L = A[0:q] y R = A[q+1:N] tal que todo elemento de L es menor o igual que A[q] y todo elemento de R es mayor o igual que A[q]. 
  2. Conquista: Ordenar L y R llamando recursivamente a Quick-Sort. 
  3. Combina: No es necesario, el arreglo ya se ordeno en los pasos anteriores.

 

def quick_sort(array,start,end):
    if start < end:
    	q = partition(array,start,end)
        quick_sort(array,start,q-1)
        quick_sort(array,q+1,end)

Divide:

def partition(array,start,end):
    x = array[end]
    i = start-1
    for j = start to end-1
    	if array[j] <= x
        	i += 1
            array[i],array[j] = array[j],array[i]
    array[i+1],array[end] = array[end],array[i+1]
    return i+1

Conquista:

Complejidad de Quick Sort ?

Divide and conques

By Mateo Sanabria Ardila

Divide and conques

  • 481

More from Mateo Sanabria Ardila