Programación dinámica
Mateo Sanabria Ardila
ISIS1105: Diseño y análisis de algoritmos

PD: Programación dinámica
Un algoritmo basado en programación dinámica resuelve un problema una única vez y lo almacena para utilizarlo mas adelante de ser necesario
-
Almacenar
-
Reusar soluciones subproblemas que ayudan a solucionar el problema
\small{PD \approx Suproblemas \ ('dividir') + \ 'reutilizar'}
Top-Down
-
Se guarda una tabla con las soluciones de los problemas resueltos hasta el momento.
-
Si la solución ya esta simplemente se retorna. -
Si la solución no esta:-
Se llama recurrentemente a los subproblemas
-
Se calcula la solución
-
Se guarda en la tabla
-
bottom-up
-
Se busca dar una noción de 'tamaño' para los subproblemas.
-
Basado en el orden dado por el 'tamaño' del subproblema, se resuelve de menos a mas.
-
Se soluciona el problema 0, luego el 1, luego el 2,...
Fibonacci
F(n) =
\left\{
\begin{array}{lr}
1 & \ n=1,2\\
\small{F(n-1)+F(n-2)} & n > 2
\end{array}
\right\}
def fibonacci(n):
if n == 1 or n === 2:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)Fibonacci
def fibonacci(n):
if n == 1 or n === 2:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)Es una muy mala implementación de fibonacci, por que?, que tan mala?
PD: Fibonacci(Top-Down)
fibonacci_memo={}
def fibonacci(n):
if(n in fibonacci_memo):
return fibonacci_memo[n]
elif n==1 or n==0:
val = 1
else:
val = fibonacci(n-1) + fibonacci(n-2)
fibonacci_memo[n] = val
return valPD: Fibonacci(bottom-up)
fibonacci_memo = {}
def fibonacci(n):
for k in range(0,n):
if k < 2:
f = 1
else:
f = fibonacci_memo[k-1]
+ fibonacci_memo[k-2]
fibonacci_memo[k] = f
return fibonacci_memo[n]
PD: Fibonacci
Se puede mejorar para tener complejidad espacial constate y complejidad temporal lineal?
def fibonacci(n):
for k in range(0,n):
if k < 2:
last = 1
last_last = 1
g = 1
else:
g = last + last_last
last, last_last = g, last
return g
Rod Cutting Problem
Rod cutting problem
Problema: Encontrar la mejor forma de cortar una varilla de longitud n
-
Una varilla de longitud i tiene asociado un precio de pi.
-
Basado en los precios se debe encontrar el mejor conjunto de cortes para obtener los máximos ingresos.
Rod cutting problem
| longitud | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| precio | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 |
| Cortes | - | 1,3 | 2,2 | 3,1 | 1,1,2 | 1,2,1 | 2,1,1 | 1,1,1 |
|---|---|---|---|---|---|---|---|---|
| valor | 9 | 9 | 10 | 9 | 7 | 7 | 7 | 4 |
De cuantas formas se puede cortar la varilla de longitud n?
Por ejemplo para una varilla de tamaño n se tiene
Rod cutting problem
Tome ri como la mayor ganancia para una varilla de longitud i, no te que:
\small{r_1 = p_1 }\\
\small{r_2 = max(p_2,p_1 + p_1)}\\
\small{r_3 = max(p_3,p_1+p_2,p_2 + p_1,p_1 + p_1 + p_1)}\\
\small{r_4 = max(p_4,p_3+p_1,\cdots,p_1+p_1+p_1+p_1)}\\
\vdots
Rod cutting problem
\small{r_1 = p_1 }\\
\small{r_2 = max(p_2,p_1 + p_1)}\\
\small{r_3 = max(p_3,p_1+p_2,p_2 + p_1,p_1 + p_1 + p_1)}\\
\small{r_4 = max(p_4,p_3+p_1,\cdots,p_1+p_1+p_1+p_1)}\\
-
Note que existen muchos cálculos que se repinten!
-
Se puede dividir y conquistar!
Rod cutting problem
r_4 = max(p_4,r_1 + r_3, r_2 + r_2, r_3 + r_1)
\small{r_k = max(p_k,r_1 + r_{k-1}, r_2 + r_{k-2},\cdots, r_{k-1} + r_1)}
Se puede mejorar aun mas!
\small{r_k = max(p_k,p_1 + r_{k-1}, p_2 + r_{k-2},\cdots, p_{k-1} + r_1)}
Rod cutting problem
# No python
def CUT-ROD(p,n):
if n == 0
return 0
q = -infinity
for i in 1 .. n
q = max(q, p(i) + Cut-Rod(p, n-i))
return qRCP: Top-down
# No python
def TOP-DOWN-CUT-ROD(p,n):
r = []
for i in 1 .. n
r[i] = -infinity
return TOP-DOWN-CUT-ROD-AUX(p,n,r)
def TOP-DOWN-CUT-ROD-AUX(p,n,r):
if r[n] >= 0
return r[n]
if n == 0
q = 0
else
q = -infinity
for i in 1 .. n
q = max(q,p[i] + TOP-DOWN-CUT-ROD-AUX(p,n-i,r))
r[n] = q
return qRod cutting problem
BOTTOM-UP
# No python
def BOTTON-UP-CUT-ROD(p,n):
r = [0] * n
for j in 1 .. n
q = -infinity
for i in 1 .. j
q = max(q,p[i] + r[j-i])
r[j] = q
return r[n]-
Graficar el problema
-
Econtrar como dividir los subproblemas
-
Econtrar relaciones entre los subproblemas
-
Identificar los casos base -
Identificar el 'nombre' de los estados -
Generalizar la relación del paso anterior (E.R) -
Identificar el tamaño de la tabla
-
Implementar
Un buen acercamiento para solucionar problemas usando PD
Longest increasing subsequence
LIS
LIS
Problema: Dado un secuencia de números encontrar la longitud de la subsecuencia creciente mas larga
LIS([-1, \ 0, \ 8, \ 6, \ 3, \ 7, \ 10, \ 4]) \ = \ ?
LIS
Problema: Dado un secuencia de números encontrar la longitud de la subsecuencia creciente mas larga
LIS([\textcolor{red}{-1}, \ \textcolor{red}{0}, \ 8, \ 6, \ \textcolor{red}{3}, \ \textcolor{red}{7}, \ \textcolor{red}{10}, \ 4]) \ = \ 5
LIS(\small{[-1, -8, \ -8, \ -8, \ -20 , \ -34, \ -33, \ 4]}) \ =
LIS([8, \ 8, \ 8, \ 8, \ 8]) \ =
LIS([7, \ 8, \ 19, \ 25,\ -5, \ 25 ]) \ =
LIS([7, \ 8, \ 19, \ 25,\ -5, \ 28 ]) \ =
3
1
4
5
¿Antes de hacer DP, como es la solución basada en una estrategia de dividir y conquistar?
LIS: como dividir subproblemas
-
Todas las subsecuencias crecientes tienen un comienzo y un final,índices en el arreglo. -
Se puede pensar un subproblema como la
subsecuencia creciente mas larga que termina en el índice k, LIS[k].
LIS: relaciones entre subproblemas
-
Que subproblemas se necesitan para solucionar el subproblema LIS[4]?
-
Revisar el valor de LIS[j] para todos los j que están conectados con el nodo en el índice 4
-
Así, LIS[4] es el mayor LIS[j] que este relacionado con el elemento en el índice 4 mas 1.
LIS: Generalizar la relación
\small LIS[n] = 1 + \textbf{max}\{ LIS[i] \ | \ i < n \ : A[i] < A[n] \}
LIS: Implementar

LIS: Implementar
#longest increasing subsequence
def lis(array):
l = len(array)
# Inside LIS we want to record the subproblem LIS[i]
# i.e LIS[i] contains the longest increasing subsequence
# that ends at i. LIS is initialized with all records in 1
# because an unary array has lis 1
LIS = [1] * l
for i in range(1,l):
subproblems = []
# The idea is to test each increasing subsequence ending at i
for k in range(i):
# if the k element keeps the subsequence increasing
# the recorded LIS at k should be store
if array[k] < array[i]:
subproblems.append(LIS[k])
# The LIS at i should be the max of the LIS for the subproblems
# plus one because i is a new element of the sequence.
# Notice tha if subproblems is empty LIS[i] don't change.
# subproblems empty means that there is no lower element that
# array[i] for all j<i
# In this case default means that max([],default=0) = 0
LIS[i] = 1 + max(subproblems,default=0)
#return the max longest increasing subsequence
return max(LIS,default=0)
LIS: Implementar
def lis(array):
l = len(array)
LIS = [1] * l
max_LIS = 0
for i in range(1,l):
max_lis_sub = 0
for k in range(i):
if array[k] < array[i]:
max_lis_sub = max(max_lis_sub,LIS[k])
max_LIS = max(1 + max_lis_sub, max_LIS)
LIS[i] = 1 + max_lis_sub
return max_LIS
Note que es posible mejorar la complejidad espacial
LIS: Implementar
def lis(array):
l = len(array)
LIS = [1] * l
max_LIS = 0
for i in range(1,l):
for j in range(i):
if array[j] < array[i]:
if 1 + LIS[j] > LIS[i]:
LIS[i] = 1 + LIS[j] Una alternativa que quizas sea mas clara
EDIT distance
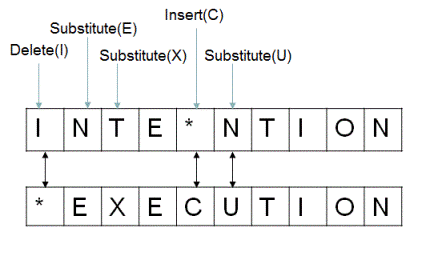
Es una forma de cuantificar cuán diferentes son dos strings entre sí.
Se busca el número mínimo de operaciones necesarias para transformar una cadena en la otra.
Se definen tres operaciones:
-
Sustitución: Remplazar un único carácter en W1 con uno diferente para internar alcanzar W2.
-
Insertar: Insertar un único carácter en W1 para internar alcanzar W2.
-
Eliminación: Eliminar un único carácter de W1 para internar alcanzar W2.
W1W2
Algunos ejercicios de LeetCode
-
70. Climbing Stairs -
746. Min Cost Climbing Stairs -
416. Partition Equal Subset Sum -
198. House Robber -
213. House Robber II
Programación dinámica
By Mateo Sanabria Ardila
Programación dinámica
Programación dinámica
- 887



