Greedy algorithm

Mateo Sanabria Ardila
ISIS1105: Diseño y análisis de algoritmos

Greedy algorithms Estrategia de búsqueda en la cual se elige la opción óptima en cada paso local con la idea de encontrar la solución óptima global  

1. Subestructura optima: Solucionar subproblemas "óptimamente"  significa poder solucionar el problema original "óptimamente"

2. Elección codiciosa: Elecciones locales óptimas llevan a la solución óptima global  

Greedy properties

Problema PRÁCTICO

1. Para reducir los costos operacionales de una ciudad, se ha decidido optimizar la iluminación en las calles.
2. La iluminación para un metro cuadrado por día cuesta un dólar.
3. La ciudad ha decidido apagar las luces de algunas calles.
4. Se propone una optimización en la cual haya al menos un camino iluminado desde cada cruce hasta cualquier otro cruce.
5. Dada una ciudad, cuál es la cantidad mínima que se puede gastar para iluminar las calles. 

Tree (arbol) := Es un grafo no dirigido para el cual cualquier dos nodos están conectados por  exactamente un camino i.e. un grafo conectado acíclico 

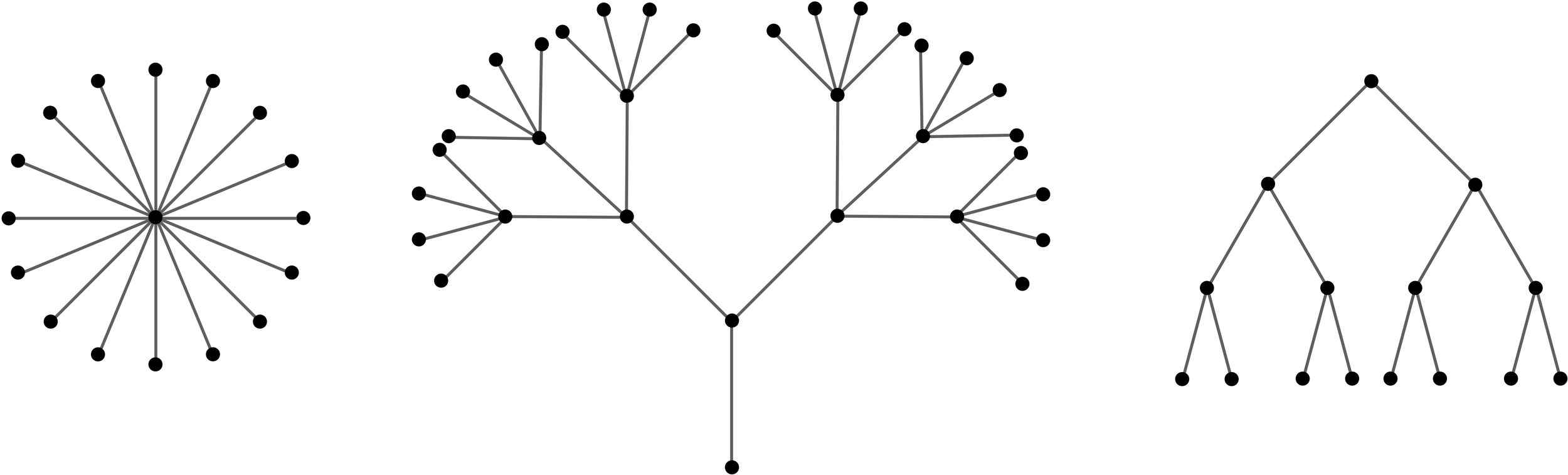
Spanning Tree (árbol de recubrimiento)  

Dado un grafo G=(V,E) un ST es un arbol S tal que

S es un Subgrafo que es un árbol que alcanza todos los nodos de G

MST: Minimum spanning tree


Dado un grafo cargado G=(V,E) un MST es un spanning tree S de G tal que la suma de los pesos los arcos de S es mínima

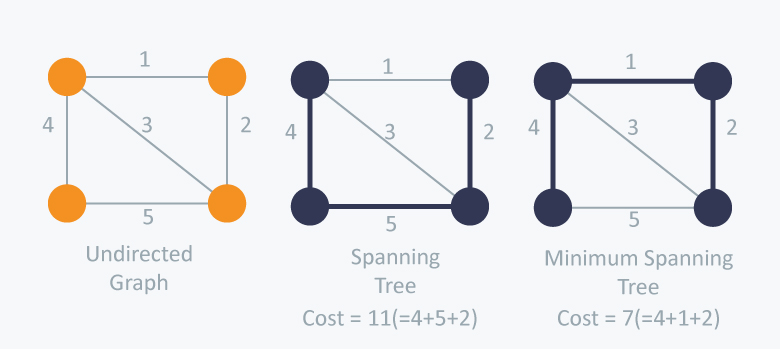
Problema PRÁCTICO

1. Para reducir los costos operacionales de una ciudad, se ha decidido optimizar la iluminación en las calles.
2. La iluminación para un metro cuadrado por día cuesta un dólar.
3. La ciudad ha decidido apagar las luces de algunas calles.
4. Se propone una optimización en la cual haya al menos un camino iluminado desde cada cruce  hasta cualquier otro cruce.
5. Dada una ciudad, cuál es la cantidad mínima que se puede gastar para iluminar las calles.

Como solucionar el problema?

Solution Overview 

1. Escoger un camino (e) que pertenezca al MST
2. Hacer una contracción con (e) sobre el grafo
3. Añadir (e) al MST 
4. Iterar sobre la contracción 

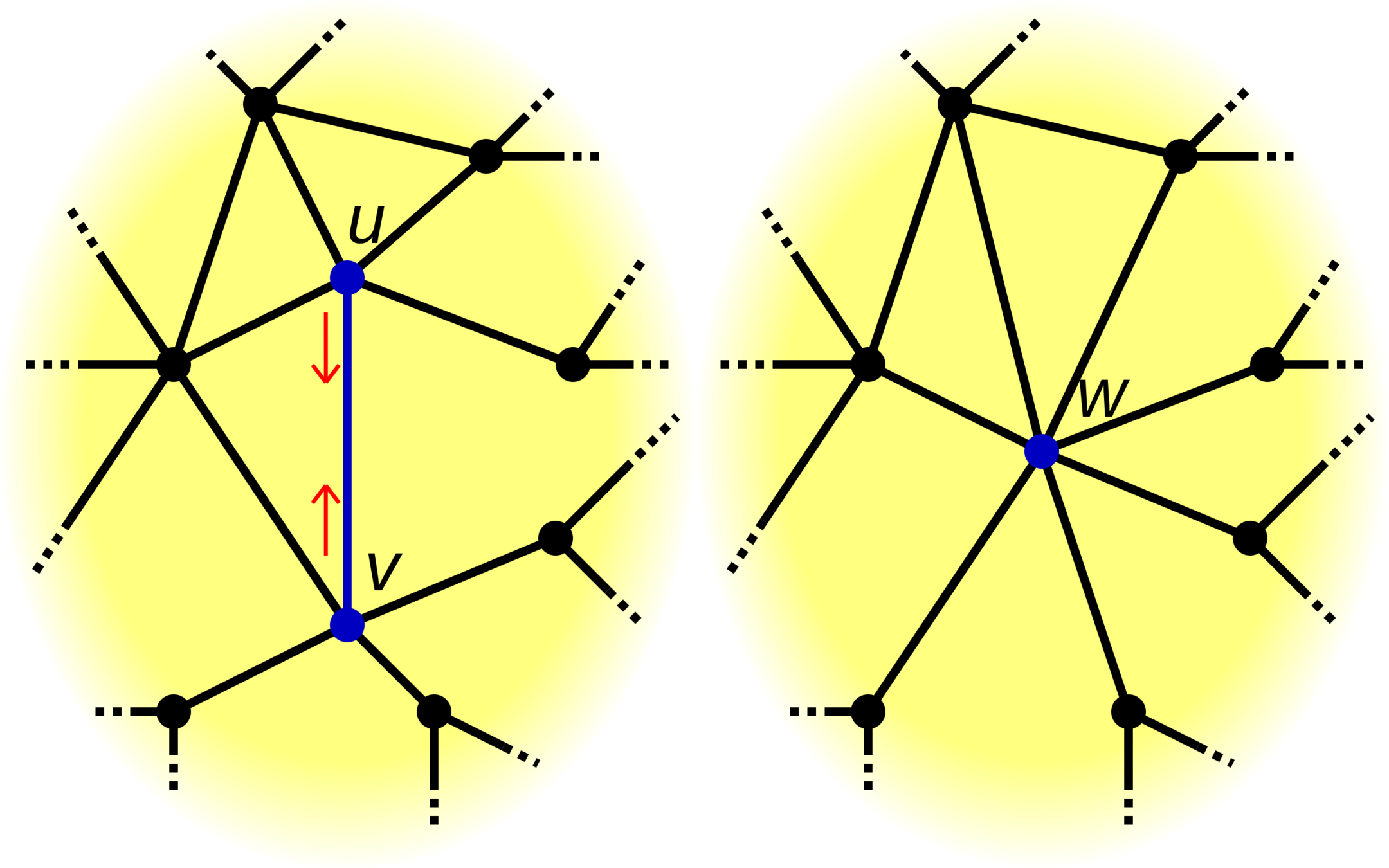
Algoritmo de Prim

Algoritmo de Kruskal

Board Time!