IntratabilidaD
In a nutshell
Mateo Sanabria Ardila
ISIS1105: Diseño y análisis de algoritmos

Un problema X se define como un conjunto de parejas (p,r), donde p es una pregunta y r una respuesta. PX es el conjunto de preguntas de X.
P_X = \{\ p \ | \ (p,r) \in X \ \}
Clasificación de problemas en base al carácter de las preguntas y las respuestas:
-
Funcional: Para cada p en Px existe un único r tal que (p,r) está en X.
-
Decision: Las únicas respuestas son True o False -
Conteo: Las respuestas son números naturales
-
Busqueda: las preguntas plantean búsquedas en espacio determinados.
Un algoritmo A soluciona un problema X sii
(\forall p \in P_X \ | \ A(p) = r \ : \ (p,r) \in X )
ORDEN DE COMPLEJIDAD
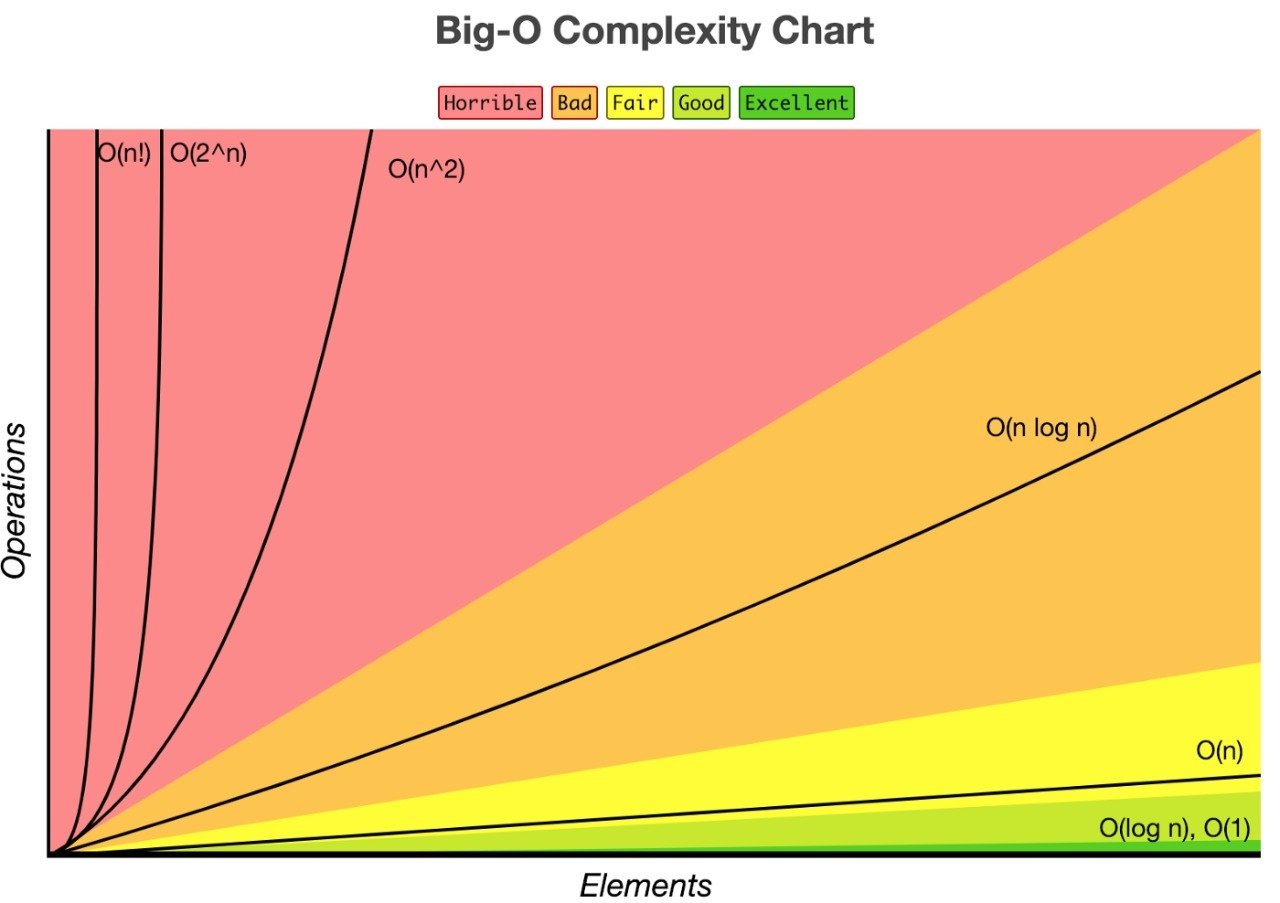
Ejemplo de problemas
-
Verificación de primalidad: Dado un entero positivo n, decidir si n es primo o no.
-
Coloración de grafos: Dados un grafo G y un entero positivo k, decidir si G es k-coloreable, i.e, si se puede colorear con k o menos colores.
-
Clique: Dado un grafo G, con n vértices, y un número natural k, decidir si existe un subgrafo completo de G, con k vértices
- ...
Problemas 'dificiles'
No se han encontrado algoritmos polinomiales para resolverlos, pero tampoco se ha podido probar que no los haya! Existen algoritmos que dan respuesta
-> Pero en tiempo exponencial
Existen algoritmos que dan 'respuesta' en tiempo polinomial -> Pero es una respuesta aproximada o 'poco confiable'
NP-completitud: overview
Los problemas NP-Completos se pueden caracterizar, informalmente, como:
-
Si se encuentra un algoritmo que resuelva un problema NP-Completo en tiempo polinomial entonces se tiene un algoritmo para resolver cualquier problema NP-completo. -
Si se prueba que un problema NP-Completo no se puede solucionar en tiempo polinomial. Entonces no existe solución polinomial para cualquier problem NP-Completo.
DECISIÓN vs
Optimización-Búsqueda
Normalmente la intratabilidad está relacionada con problemas de decisión. Sin embargo,para algunos problemas es más 'interesante' conocer si se tiene la respuesta correcta.

Para algunos problemas es lo mismo!
problema del viajero
Dadas n ciudades en un plano, encontrar la longitud minima de tour (camino cerrado que no repite nodos) que visita las n ciudades
\small m = (\uparrow _{u,v} | u,v \in ciudades : dist(u,v))
-
Cualquier tour está acotado superiormente por n*m
-
Se tiene un algoritmo que decide AV
con el grafo G y la cota d: AV-decision-problem(G,d)
def AV-optimization-problem(G,d):
_min, _max = 0, n*m
while max-min >= 1:
d = (max + min) // 2
if AV-decision-problem(G,d):
max = d
else:
min = d+1
return d
Este algoritmo resuelve el problema de optimización del problema del viajero
Luego si el problema de decisión se logra solucionar en tiempo polinomial el problema de optimización también!
Why!?

SPOILER Si los problema de decisión y optimización se logran solucionar en tiempo polinomial el problema de busqueda también!
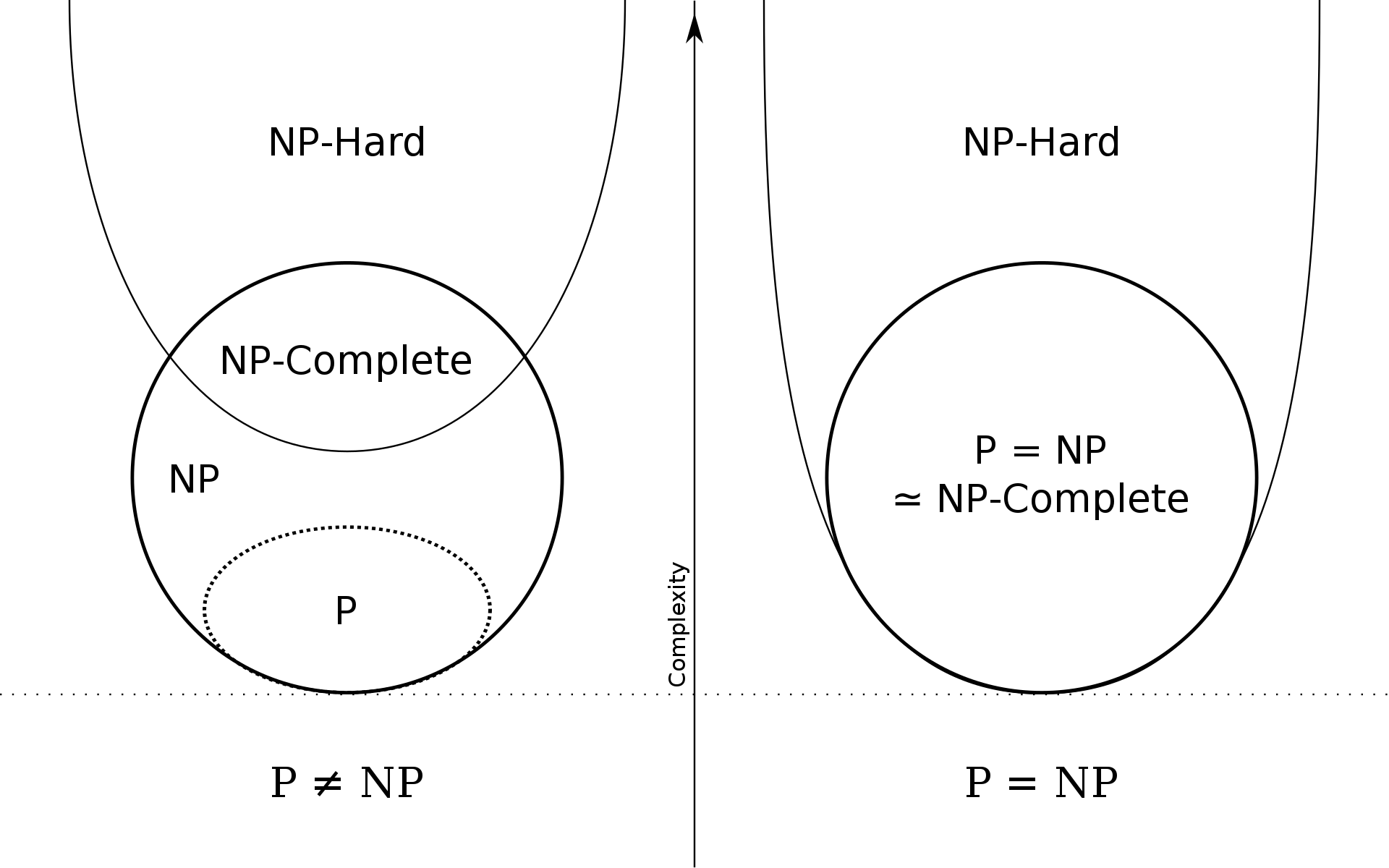
Clases de complejidad
Clase P: Está compuesta de todos los problemas de decisión que tienen solución sobre una MTD, cuyo tiempo de ejecución es de orden polinomial.
-
Recubrimiento de arcos (MST)
-
Camino de Euler
-
Solución ecuación diofántica
- ...
reducciones
Supóngase que un problema X se puede resolver en tiempo polinomial en una MTO que usa un oráculo que soluciona un problema Y.
Si Y es soluble en una MTD en tiempo polinomial, entonces X también debe ser soluble en una MTD en tiempo polinomial
turing-reduccion
Una reducción de X a Y es una MTO que resuelve X, usando un oraculo para Y
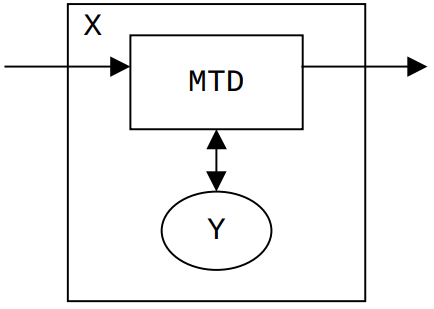
X es reducible a Y
turing-reduccion
Si X y Y son problemas de decisión una transformación de X a Y es una función, calculable en una MTD, tal que
\small (x,r) \in X \equiv (f(x),r') \in Y
Una transformación corresponde a una reducción en la que el oráculo solo es consultado una vez, y su respuesta debe coincidir con la respuesta del primer problema
\small X \leq_R Y := \text{Hay una reduccion en } R \text{ de } X \text{ a } Y
Sean X,Y problemas C una clase de problemas y R una clase de reducciones
Sean X,Y problemas C una clase de problemas y R una clase de reducciones, R es C-compatible si para cualquier par de problemas X,Y se cumple:
X \leq_R Y \ \wedge \ Y \in C \rightarrow X \in C
Sean X,Y,Z problemas y R una clase de reducciones, R es transitiva si para cualquier X,Y,Z se cumple:
X \leq_R Y \ \wedge \ Y \leq_R Z \rightarrow X \leq_R Z
La clase de las reducciones polinomiales , son las que obedecen cotas de tiempo polinomiales. En términos de la definición, la MTO resuelve X en tiempo polinomial.
Las reducciones polinomiales son transitivas y, además, P-compatibles.
completitud
\small X \ \text{es R-dificil para C := } \forall_{y \in C} \ Y \leq_R X
Sean X un problema, C una clase de problemas y R una clase de reducciones
\small X \ \text{es R-completo para C := } \\ X \ \text{es R-dificil para C} \wedge X\in C
Clases de complejidad
Clase NP: A la clase NP pertenecen los problemas de decisión que tienen una solución sobre una MTND, cuyo tiempo de ejecución es de orden polinomial.
Si una MTND se enfrenta en dos ocasiones a una misma configuración, la secuencia de operaciones efectuadas puede diferir de una a otra ejecución
Un problema X es NP-completo si pertenece a la clase NP y cualquier problema Y de NP es reducible a X.
Si llamamos RP a la clase de las reducciones polinomiales un problema es NP-completo si es RP-completo para NP.
Intratabilidad
By Mateo Sanabria Ardila
Intratabilidad
Intratabilidad
- 426



