IntratabilidaD
Mateo Sanabria Ardila
ISIS1105: Diseño y análisis de algoritmos

Problemas NP
-
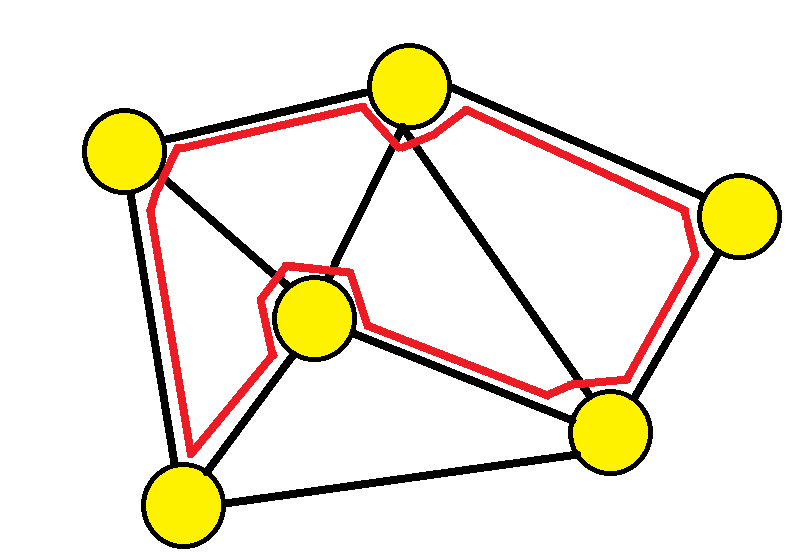
Longest simple path
-
Hamiltonian cycle
-
3-CNF satisfiability
Problemas NP
-
Longest simple path
-
Hamiltonian cycle
-
3-CNF satisfiability
Problemas NP
-
Longest simple path
-
Hamiltonian cycle
-
3-CNF satisfiability
(x_1 \vee x_2 \vee x_3) \wedge \neg(x_1 \wedge x_2 \wedge x_3)
Euler tour
Dado un grafo conectado dirigido G, es un ciclo que recorre cada arco de G exactamente una sola vez, se puede visitar cada nodo mas de una vez.
Hamiltonian cycle
Dado un grafo dirigido G, es un ciclo que contiene todo los nodos de G.
P
NP

Shortest simple path
Longest simple path

P
NP
Objetivo
Objetivo

Objetivo
Entender a porque si cualquier Problema NPC puede ser resuelto en tiempo polinomial entonces cualquier problema NP tiene un algoritmo que corre en tiempo polinomial

Un problema abstracto Q es una relación binaria de un conjunto I de instancias del problema y un conjunto S de soluciones
Un problema abstracto de decisión es una función que mapea instancias de I en el conjunto solución {0,1}
Por ejemplo el problema de decisión PATH donde el conjunto de instancias es:
I = \{ \langle G,u,v,k \rangle | G = (E,V) \wedge \{u,v\}\in V \wedge k \in \mathbf{N} \}
Donde:
PATH(\langle G,u,v,k \rangle) = 1
Si un camino entre u y v tiene como máximo k arcos.
e.o.c
PATH(\langle G,u,v,k \rangle) = 0
Un Encoding de un conjunto S de objetos abstractos es un mapeo
e: S \rightarrow \{0,1\}^{*}
Por ejemplo, un enconding usual para los números naturales:
e(17) = 10001
Polinomios, grafos, funciones, pares ordenados, programas... todo puede ser codificado en strings binarias
La forma en la que se hace la codificación podría afectar, pero para efectos prácticos suponemos que siempre lo hacemos de la mejor forma posible...
Un lenguage L sobre
\Sigma
es cualquier conjunto de
palabras armadas con los símbolos de
\Sigma
\Sigma
Un alfabeto
es un conjunto finito de símbolos
denota la palabra vacía
\varepsilon
denota el lenguaje vacío
\emptyset
\Sigma^*
el lenguaje de todas las palabra sobre
\Sigma
Q esta caracterizado por las instancias del problema que producen 1, entonces Q se puede entender como el lenguaje L sobre = {0,1}:\Sigma
L = \{x \in \Sigma^* : Q(x) = 1\}
El conjunta de instancias para cualquier problema de decisión Q es el conjunto
\Sigma^*
Q esta caracterizado por las instancias del problema que producen 1, entonces Q se puede entender como el lenguaje L sobre = {0,1}:\Sigma
L = \{x \in \Sigma^* : Q(x) = 1\}
Por ejemplo:
PATH = {<G,u,v,k> : G = (V,E) es un GNDu, v in V
K es un entero positivo
existe un camino de u -> v con máximo k arcos }
Relación entre los problemas y los algoritmo que los resuelven:
-
Un algoritmo A acepta una palabra x in {0,1}* si para x la respuesta de A(x) es 1. -
El lenguaje aceptado por un algoritmo A es el conjunto de palabras que el algoritmo acepta:
L = \{x \in \{0,1\}^*: A(x) = 1 \}
Un lenguaje L es decidido en tiempo polinomial por un algoritmo A si existe un constante k tal que para cualquier palabra x in {0,1}* de longitud n, el algoritmo correctamente decide si x in L en tiempo O(n^k)
Un lenguaje L es decidido por un algoritmo A si cualquier palabra binaria en L es aceptada por A y cualquier palabra que no sea de L es rechazada por A.
Clases de complejidad (P)
P = \{ L \subseteq \{0,1\}* : \\ \text{Existe un algoritmo A que decide a L en tiempo } O(n^k) \}
¿Suma de dígitos divisible por 3?
Dado un número decimal positivo n, ¿la suma de sus dígitos es divisible por 3?
DIV3 = \{ n : \sum \text{dígitos}(n) \bmod 3 = 0 \}
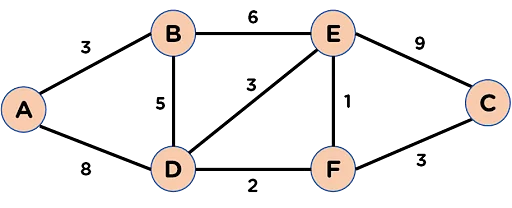
¿Existe un camino de costo ≤ K?
Dado un grafo con pesos no negativos, dos nodos u y v, y un entero K, ¿existe un camino de u a v de costo ≤ K?
PATH = \{ (G, u, v, K) : \\ \exists \text{ camino de } u \text{ a } v \text{ de costo } \leq K \}
¿Patrón en el texto?
Dado un texto T y un patrón P, ¿ocurre P dentro de T?
MATCH = \{ (T, P) : P \text{ aparece en } T \}
¿Está ordenada la lista?
Dada una lista de números, ¿están en orden no decreciente?
SORTED = \{ LIS : LIS[i] \leq LIS[i+1] \ \forall i \}
Un algoritmo A de verificación es una algoritmo de dos parámetros. Donde uno de los es una palabra del lenguaje y el segundo es un certificado del problema.
Un algoritmo A verifica una palabra x si existe un certificado y tal que: A(x,y) = 1.
El lenguaje verificado por un algoritmo de verificacion A es:
L = \{ x \in \{0,1\}* : (\exists y \in \{0,1\}*: A(x,y)=1) \}
Un lenguaje L pertenece a NP sii existe un algoritmo A y una constante c tal que:
Clases de complejidad (NP)
L = \{x \in \{0,1\}* : \\ (\exists y \in \{0,1\}*| A \in O(|x|^c) : A(x,y)=1) \}
Un ciclo Hamiltoniano (CH) es un camino sin vértices repetidos que recorre todos los vértices del grafo. Un grafo que contiene un CH se llama Hamiltoniano.
Hamiltonian cycle
HAM-CYCLE = {<G>: G es Hamiltoniano}SAT (Satisfacibilidad Booleana)
¿Existe una asignación de valores verdadero/falso a las variables booleanas que haga verdadera toda la fórmula?
SAT = \{\phi : \phi \text{ es satisfacible} \}
Problema del Viajero(TSP)
Dado un conjunto de ciudades y distancias, ¿existe una ruta que visite todas una vez, regrese al inicio y tenga costo total ≤ K?
TSP = \{(G, c, K) : \exists \text{ ciclo hamiltoniano de costo } \leq K \}
Coloración de Grafos
¿Puedes colorear los nodos de un grafo con k colores de forma que nodos adyacentes no tengan el mismo color?
COL = \{(G, k) : G \text{ es k-colorable} \}
Vertex Cover (Cobertura de Vértices)
¿Existe un conjunto de ≤ k vértices tal que cada arista tenga al menos un extremo en el conjunto?
VC = \{(G, k) : G \text{ tiene cobertura de vértices de tamaño } \leq k \}
Sudoku (Generalizado)
Dado un tablero n×n parcialmente lleno, ¿se puede completar sin violar las reglas del Sudoku?
SUDOKU = \{T : T \text{ tiene una solución válida} \}
Problema de la Mochila (Knapsack)
Dado un conjunto de objetos con valores y pesos, ¿puedes seleccionar algunos con valor total ≥ V sin exceder capacidad W?
KNAPSACK = \{(S, W, V) : \\ \exists S' \subseteq S \text{ tal que } \sum_{x \in S'} peso(x) \leq W \text{ y } \sum_{x \in S'} valor(x) \geq V \}
Subconjunto Suma (Subset Sum)
Dado un conjunto de enteros y un número T, ¿existe un subconjunto cuya suma sea exactamente T?
SUBSETSUM = \{(S, T) : \exists S' \subseteq S \text{ tal que } \sum_{x \in S'} x = T \}
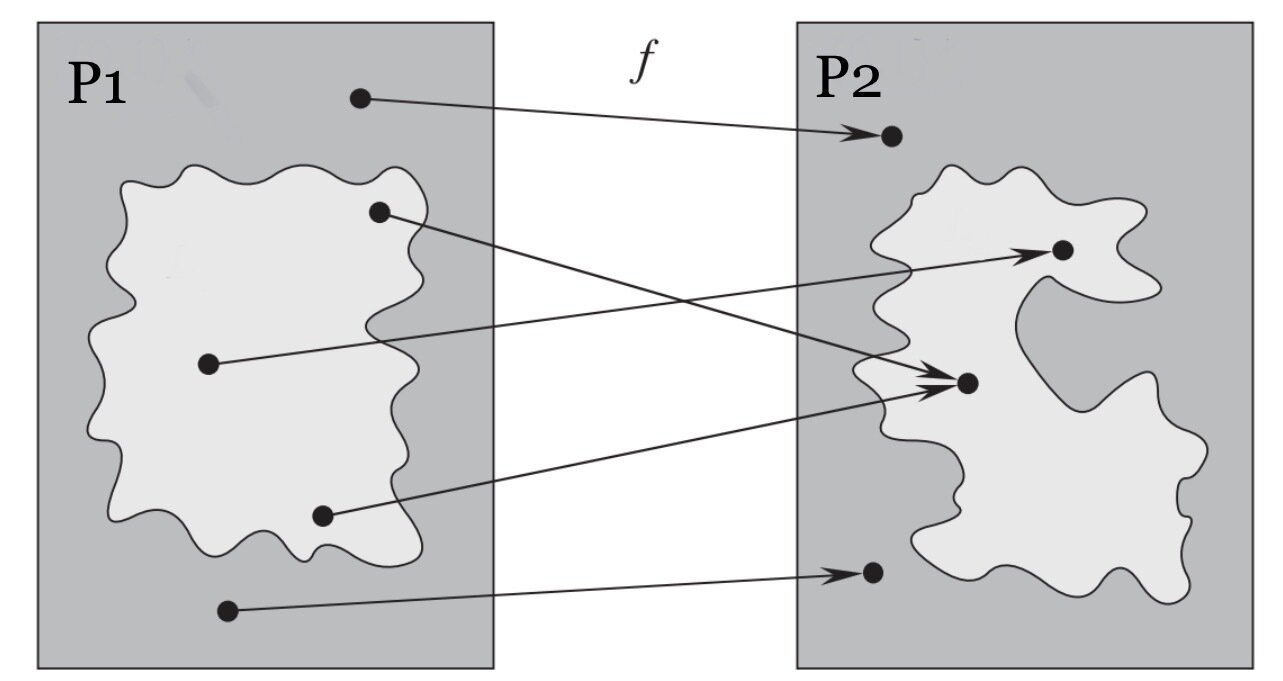
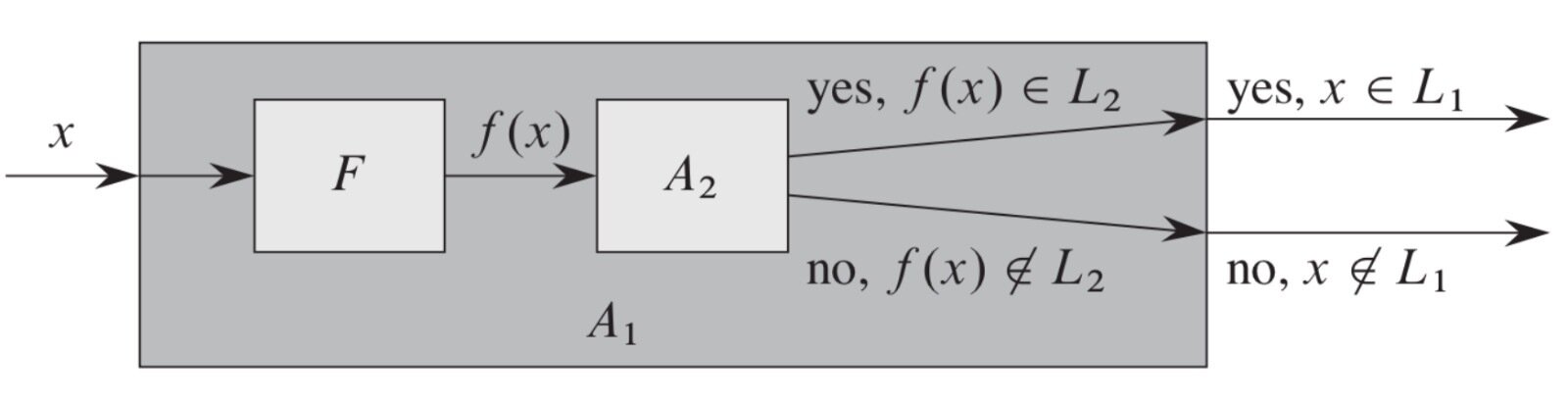
Se dice que un lenguaje L1 es reducible en tiempo polinomial a un lenguaje L2
reducciones
L_1 \leq_{\mathbb{P}} L_2
si existe una función f calculable en tiempo polinomial tal que:
x \in L_1 \equiv f(x) \in L_2
f es la función de reducción y cualquier algoritmo F que compute f en tiempo polinomial es es llamado algoritmo de reducción
x \in L_1 \equiv f(x) \in L_2
L_2 \in P \ \wedge \ L_1 \leq_P L_2 \rightarrow L_1 \in P
Un problema X es NP-Completo si:
Clases de complejidad (NPC)
1. \ \ X\in NP \\
2. \ \ (\forall_{X' \in NP}: X' \leq_p X )
NP-Dificil
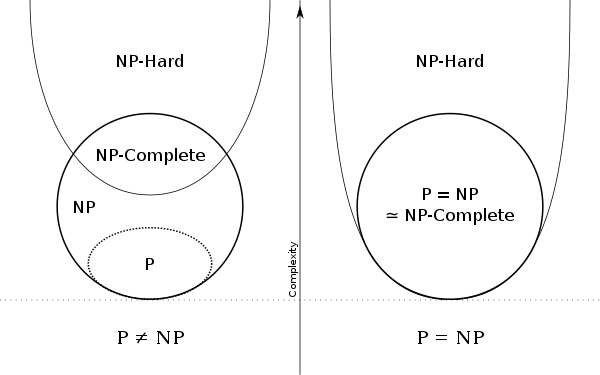
Problemas NP-DIFICILES que no sean NPC

Si cualquier problema NPC es soluble en tiempo polinomial entonces: P = NP
A little bit of history

L' \in NPC \wedge L' \leq_P L \rightarrow L \in NPH
Para que sirve saber esto?
L' \in NPC \wedge L' \leq_P L \rightarrow L \in NPH
Cuando se reduce L' a L implicitamente se esta reduciendo todo problema en NP a L. Es decir se tiene un metodo para probar que L es NP-Completo:
-
Probar que L es NP
-
Tomar un problema L' que se sabe que es NPC y econtras una reduccion polinimial de L' -> L. (Cualquier instacia de L' se puede llevar a una instancia de L en timpo polinomial manteniendo la decibilidad )
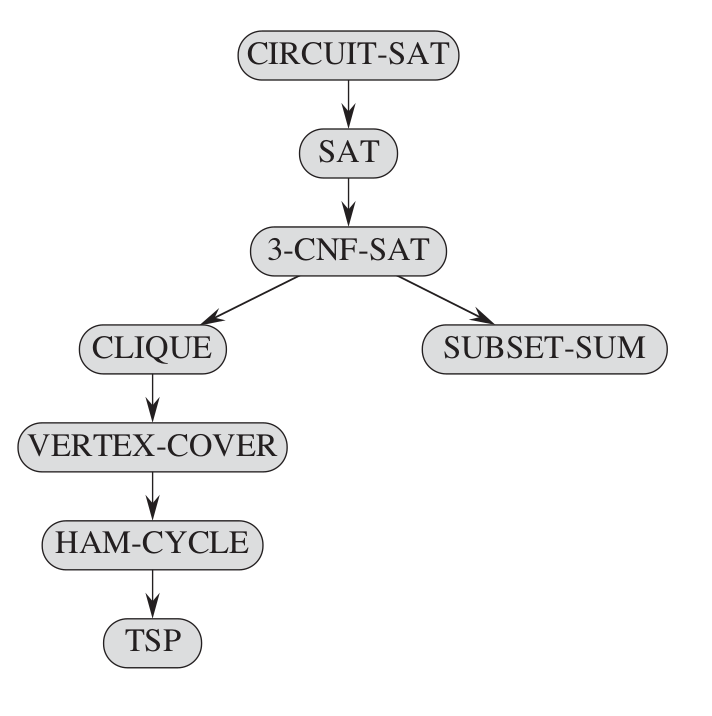
circuit sat
Cuando se pruebe que existe UN problema NP-completo se pueden usar reducciones para probar otros problemas NP-completos.
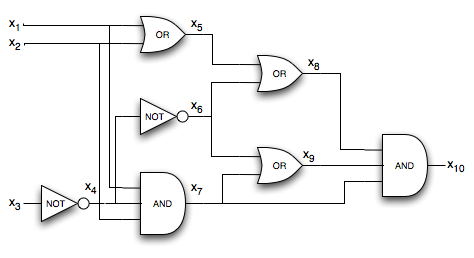
circuit sat
Los circuitos booleanos están construidos por elementos booleanos conectados por cables. Para circuit-sat se definen tres operadores booleanos (compuertas logicas) : NOT, AND y OR. Las compuertas AND y OR se generalizan para tomar mas de un parámetro de entrada:
-
AND : Si recibe 1 en todas sus entradas la salida es 1, e.o.c la salida es 0.
-
OR : Si recibe 0 en todas sus entradas la salida es 0, e.o.c la salida es 1.
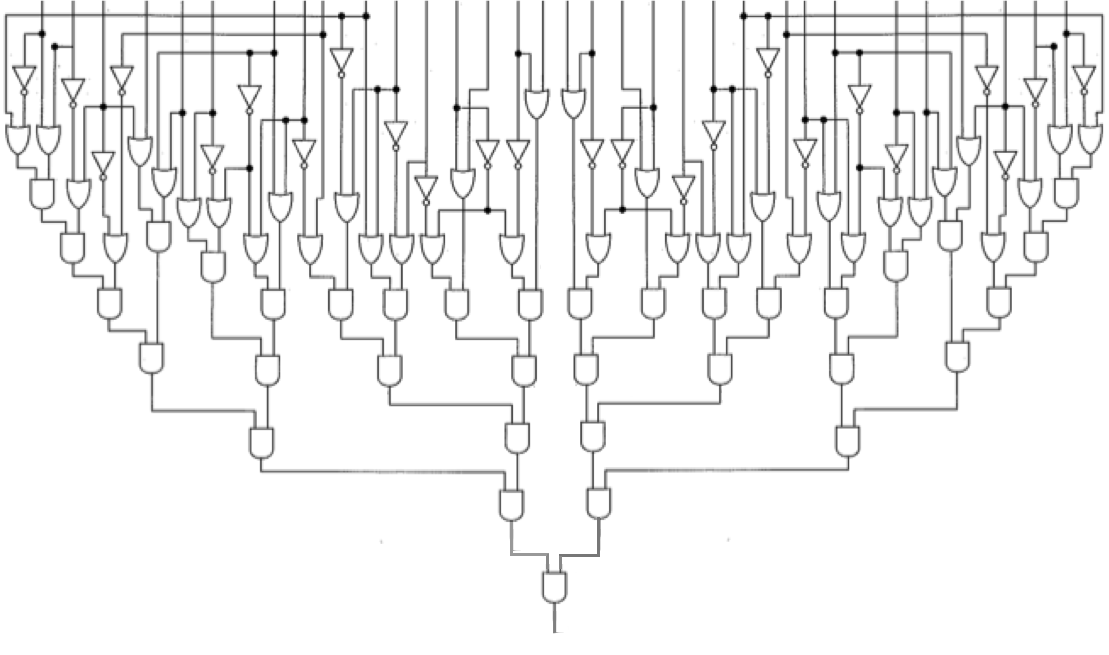
circuit sat
Formalización: Sea G = (V,E) un grafo directo con un nodo por cada compuerta del circuito y k conecciones con representando los k cables de salida de cada compuerta. Note que G no debe tener ciclos!
Circuit-Sat pertence a NP
Circuit-Sat pertence a NP-hard
Para cualquier problema L de NP, se debe describir una función f tal que:
x \in L \ \ sii \ \ f(x) \in CIRCUIT-SAT
-
Como L es NP existe un algoritmo A que verifica a L en tiempo polinomial.
-
La idea de la prueba es representar la computación de A como un secuencia de computaciones.
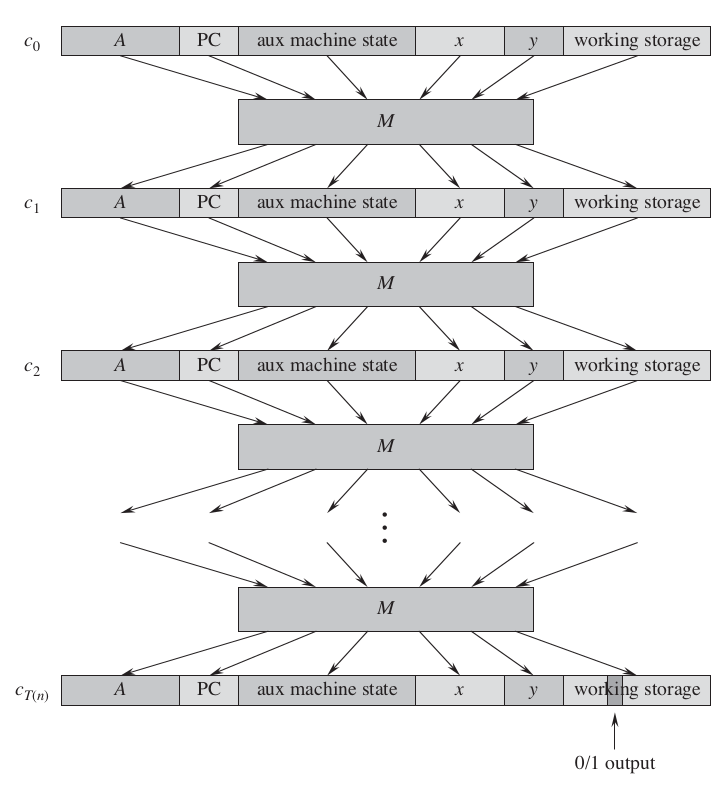
Circuit-Sat pertence a NPH
Circuit-Sat pertence a NPC
(Primer problema)

SAT
Una instancia de, SAT es una formula boolena compuesta de:
-
n variables booleanas x1,x2,...xn
-
m conectores booleanos, cualquier funcion booleana de uno o dos paremetros: AND,OR,NOT,->,<->.
-
Parentesis
SAT = \{ <\phi>: \textrm{es una formula satisfacible} \}
SAT es NPC
\textrm{Cirtcuit-SAT} \leq_p \textrm{SAT}

3-CNF
-
Un literal es una variable booleana o su negación.
-
Una clausulas son varios literales conectados por s. -
Una cnf-formula esta compuesta por varias clausulas conectadas por
Se llama una 3cnf-formula si todas las clausulas tienen tres literales.
\vee
x_1 \vee x_2 \vee \neg x_3 \vee x_4
\wedge
(x_1 \vee x_2 \vee \neg x_3 \vee x_4) \wedge (x_5 \vee \neg x_6) \wedge (x_7 \vee \neg x_8 \vee x_9)
(x_1 \vee x_2 \vee \neg x_3 ) \wedge (\neg x_4 \vee x_5 \vee \neg x_6) \wedge (x_7 \vee\neg x_8 \vee x_9)
3SAT = \\ \{ \langle \phi \rangle : \phi \text{ es una formula 3cnf satisfacible} \}
3-CNF es NPC
\textrm{SAT} \leq_p \textrm{3-CNF}

CLIQUE
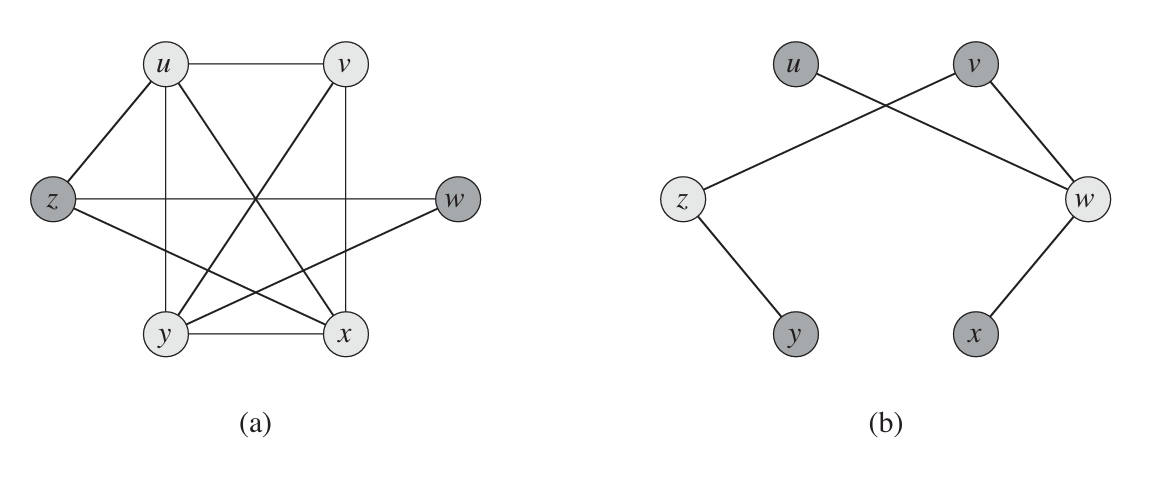
Un clique de un grafo G es un subgrafo de G donde cualquier par de nodos esta conectado. Un K-clique es un clique que contiene k nodos.
CLIQUE = \\ \{\langle G,k \rangle : \text{ G es un grafo no dirigido con un k-clique} \}
Un clique de un grafo G es un subgrafo de G donde cualquier par de nodos esta conectado. Un K-clique es un clique que contiene k nodos. 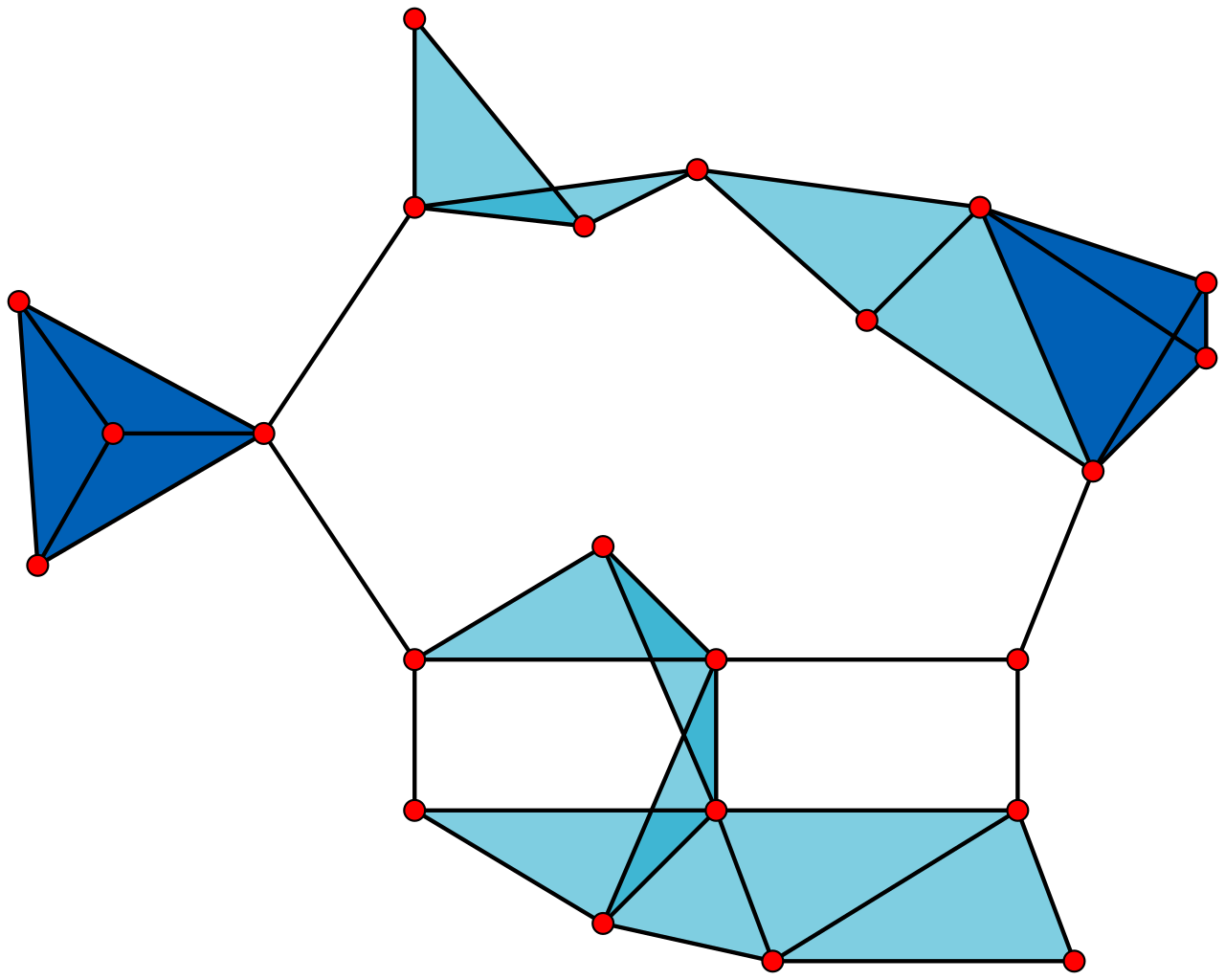

CLIQUE (Optimización)
El problema de CLIQUE (Optimización) consiste en encontrar el clique más grande en un grafo no dirigido G, es decir, el subgrafo completamente conectado con el mayor número de nodos.
\text{Maximizar } |C| \text{ tal que } C \subseteq V, \text{ y } \forall u,v \in C, (u,v) \in E
\text{CLIQUE}_\text{dec} \Rightarrow \text{CLIQUE}_\text{opt}
Si logramos resolver el problema de decision también logramos solucionar el de optimización
\text{L}_\text{dec} \Rightarrow \text{L}_\text{opt}
Si logramos resolver el problema de decision también logramos solucionar el de optimizaciónEsto sirve para cualquier problema L.Vertex-cover
Una cobertura de vértices de un grafo no dirigido G=(E,V) es un subconjunto tal que:
V' \subseteq V
(u,w) \in E \rightarrow u \in V' \vee w \in V'
El tamaño de una cobertura de vértices es la cardinalidad de V'.
Vertex-cover
(u,w) \in E \rightarrow u \in V' \vee w \in V'
G=(V,E) \wedge V' \subseteq V



Vertex-cover
(u,w) \in E \rightarrow u \in V' \vee w \in V'
G=(V,E) \wedge V' \subseteq V
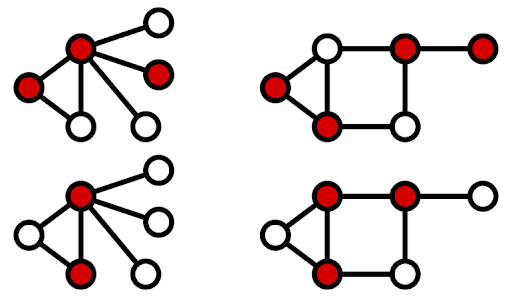
Vertex-cover
VERTEX-COVER = \{\langle G,k \rangle : \\ \text{ G tiene una cobertura de vertices de tamaño k} \}
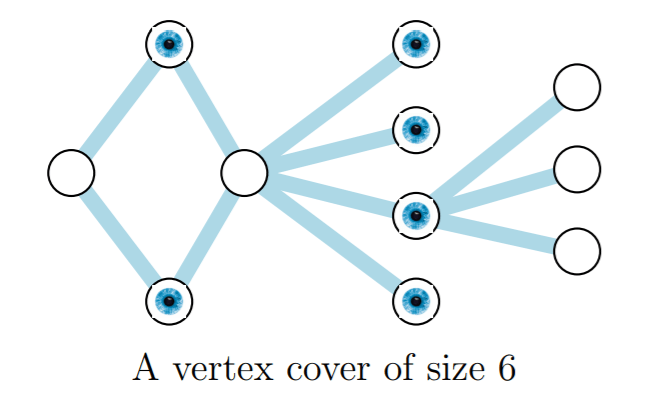
Vertex-cover ES NPC
Vertex-cover ES NP
Vertex-cover ES NP-HARD
CLIQUE \leq_{P} VERTEX-COVER

traveling salesman problem
TSP = \{ \langle G,c,k \rangle : \\ \text{ G es un grafo completo} \\ \text{c es una funcion de costo} \\ \text{G contiene un tour de costo k} \}
traveling salesman problem
traveling salesman problem
traveling salesman problem


TSP es NPC

Intratabilidad
By Mateo Sanabria Ardila
Intratabilidad
Intratabilidad
- 550



