funciones de hash

Mateo Sanabria Ardila
Introducción a la criptografía
hash != criptografía
Las funciones de hash son altamente utilizadas en CS. Sin embargo, en criptografía NO constituyen un método de cifrado. Mas bien son funciones auxiliares que se usan para:
-
Firmas digitales
-
MACs
-
RNGs
-
. . .
Una de las principales aplicaciones de las funciones de hash, en criptografia, son la firmas digitales. Por que no usar RSA o ELGAMAL??.
-
El tamaño de la firma es limitado por el tamaño de la llave.
- Archivos grandes implican firmar por bloques
Firma Digital: HASH


\tiny (z,s)
\tiny S = Sig_{K_{pr}}(Z)
\tiny Z= h(x)
\tiny Z= h(x)
\tiny VER_{K_{pub}}(Z,S)
Z es la 'Huella' del mensaje X
Requerimientos para una FUNCIÓN de hash
-
Cualquier tamaño de entrada
-
Tamaño fijo de salida
- Eficiente!!!
- Input resistance
- Weak collision resistance
- Strong collision resistance
input resistance: Dado el resultado de un función de hash debería ser imposible encontrar la entrada original
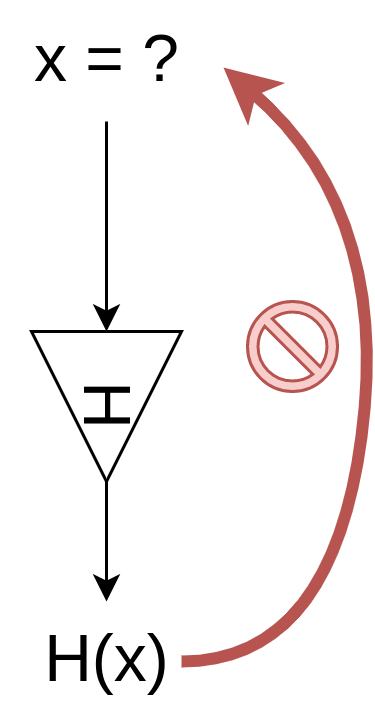
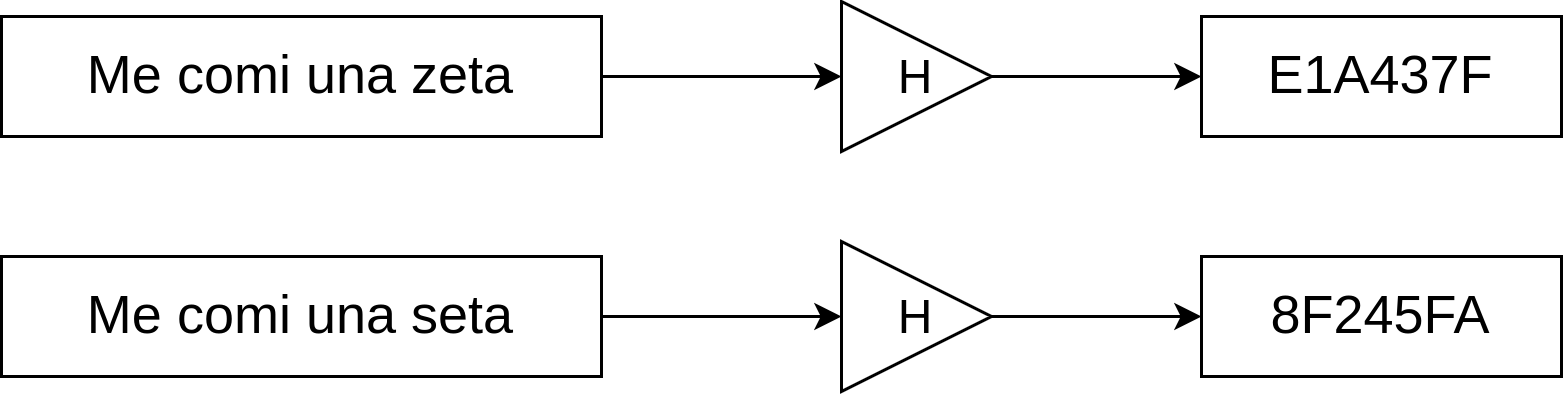
weak collision resistance: Dado x y su correspondiente hash. Deberia ser imposible tener encontrar una modificacion de X que tenga el mismo hash.
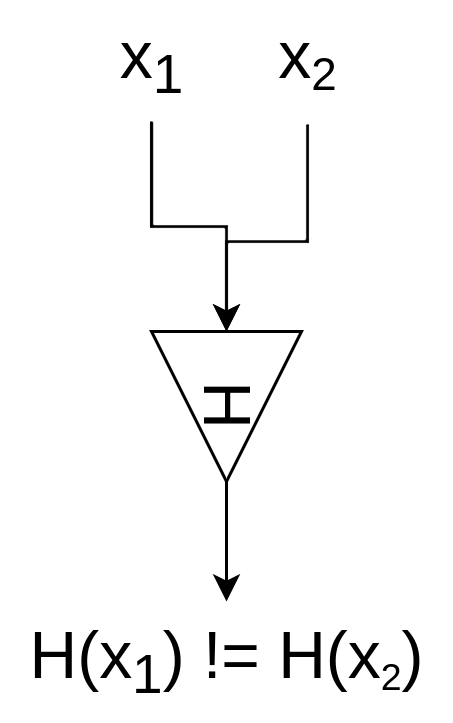
Strong collision resistance: Es computacionalmente inviable encontrar entradas X,Y tales que H(X) = H(Y). En este caso tanto X como Y pueden ser alterados para encontrar un hash idéntico.
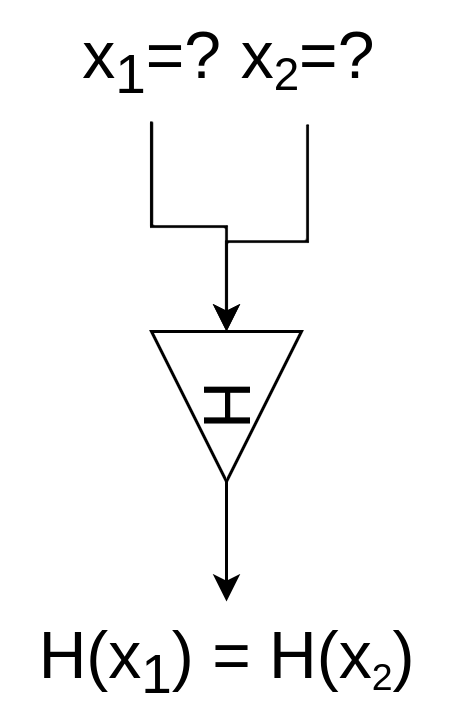
Los ataques sobre colisiones son MUCHO más difíciles de prever que un ataque sobre la entrada!
Se puede definir una función de hash que no tenga colisiones?

Hablemos de cumpleaños

Cuantas personas deben estar reunidas para que al menos dos cumplan el mismo día?
X(t) := 'No \ colisiones \ entre \ t \ personas'
P(X(2)) = 1 - \frac{1}{365}
P(X(3)) = (1 - \frac{1}{365})(1 - \frac{2}{365})
P(X(t)) = \prod_{i=1}^{t}(1 - \frac{i}{365})
Funciones de Hash
By Mateo Sanabria Ardila
Funciones de Hash
Firmas Digitales
- 173



