
Mateo Sanabria, Leonardo Angel, Nicolás Cardozo
Safety Verification of the Raft Leader Election Algorithm using Athena
17 Congreso Colombiano de ComputaciónMedellin, Ago 11 2023

RAFT
Consensus algorithm for managing a replicated log
ACtors
Athena
+
+
Basic building block of concurrent computation
Language for expressing proof and computations
1
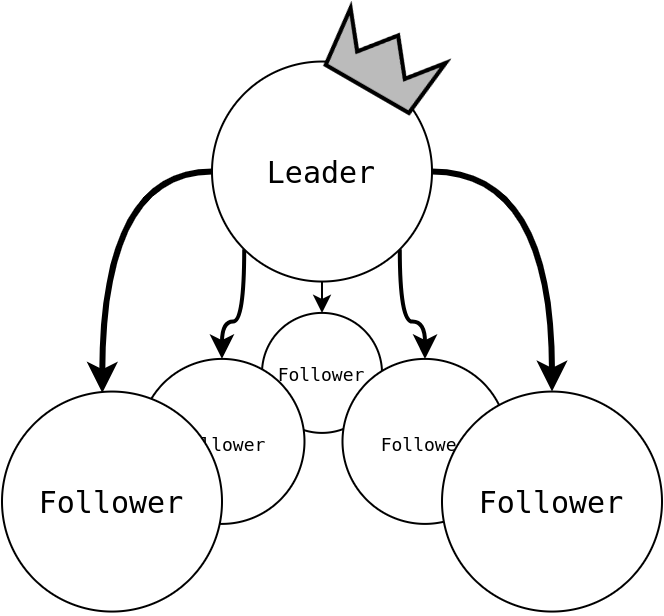
Leader election
In an raft cluster with n nodes there is leader node and n-1 follower nodes. The leader is in charge of keeping the communication with the client an maintaining the log replication across the cluster
2
Expect regular heartbeats
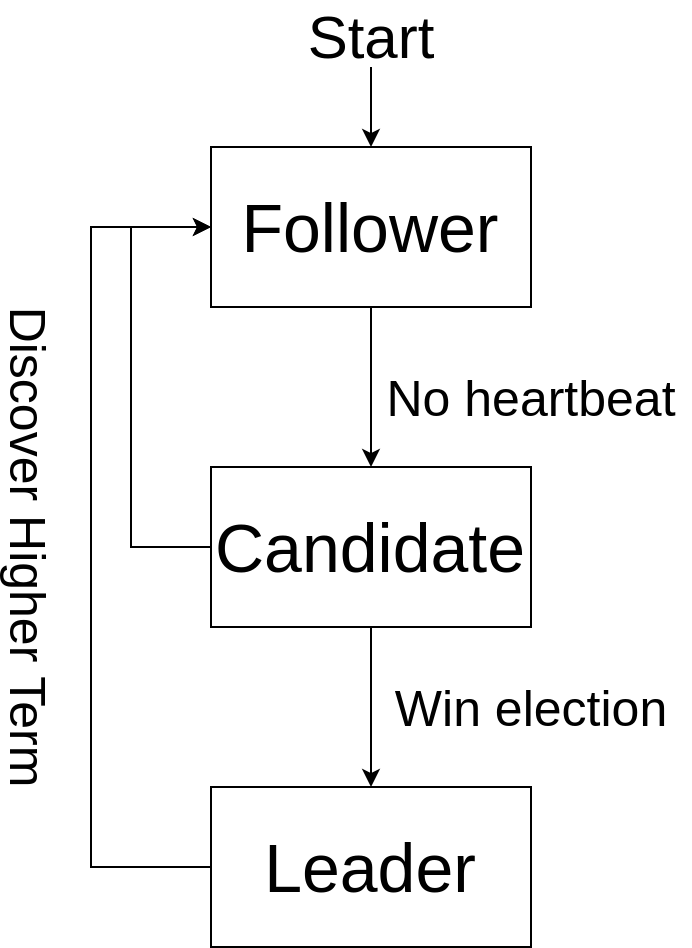
RAFT: Leader election
Proposes as candidate when does not get heartbeats
Sends heartbeats
3
specification of RAFT Nodes USING ATHENA
datatype NLS := Follower | Candidate | Leader
datatype Alias := Jessie | James | Meowth
datatype Name := (Name Alias N)
datatype FLS := (Following Alias N)
datatype CLS := (Local N)
datatype Log := (State NLS CLS FLS)
datatype RAFTLS := (Node Log Name) Each node is specified as an actor capable of sending and receiving messages.
4
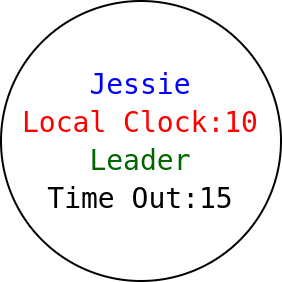
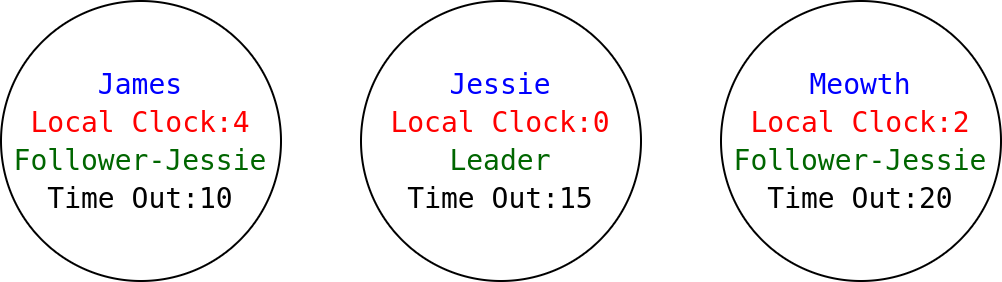
ATHENas' RAFT Nodes
(Node
(State Follower (Local 2)
(Following Jessie 0)) (Name Meowth 20)) ++
(Node
(State Leader (Local 0)
(Following Jessie 3)) (Name Jessie 15)) ++
(Node
(State Follower (Local 4)
(Following Jessie 0)) (Name James 10)) 5
Node local computations are used to express the behavior of nodes in the form of two function definitions: next and ready-to
declare next: [RAFTLS (Step Alias)] -> RAFTLS
declare ready-to: [RAFTLS (Step Alias)] -> BooleanWhen receiving a message, actors can modify their internal state, create new actors with predefined behavior, or send messages to known actors.
datatype (Step Id) := (receive Id Id Ide)
| (send Id Id Ide)
| (create Id Id) 6
The idea is to describe the behavior of the raft leader election process using such functions
7
'propose'tick'propose'broadcast'broadcast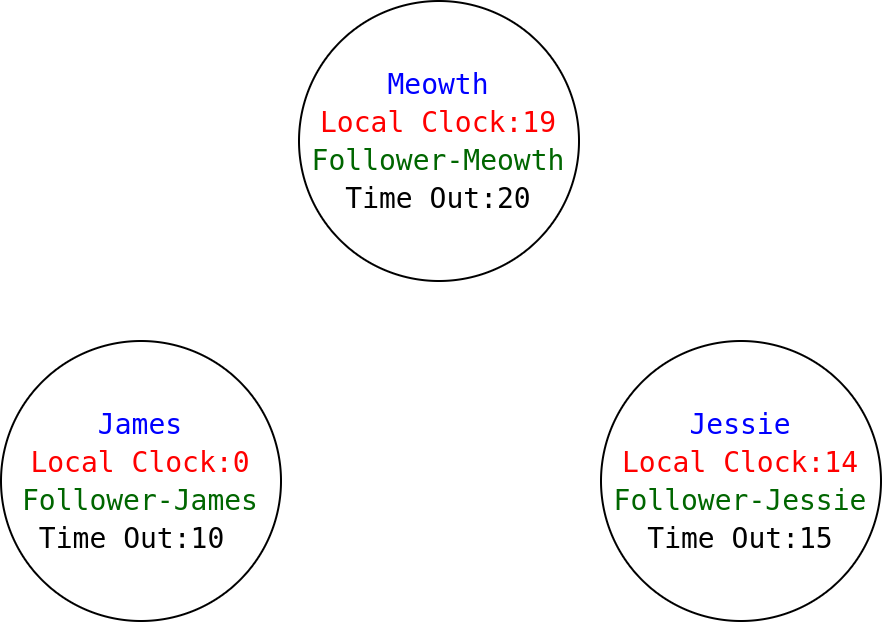
The idea is to describe the behavior of the raft leader election process using such functions
8
'tick'tick'tick'approve'approve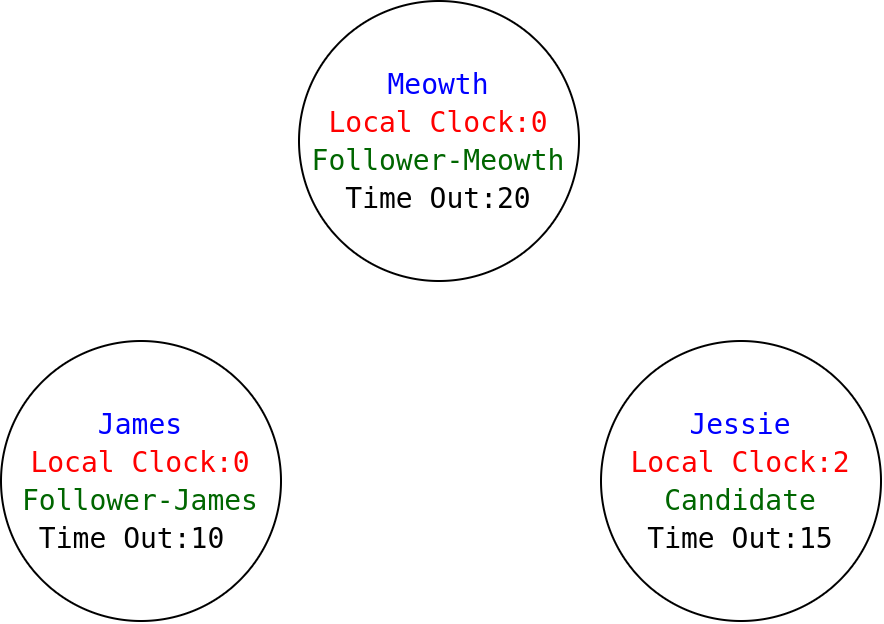
The idea is to describe the behavior of the raft leader election process using such functions
9
'tick'tick'tick'broadcastApprove'broadcastApprove
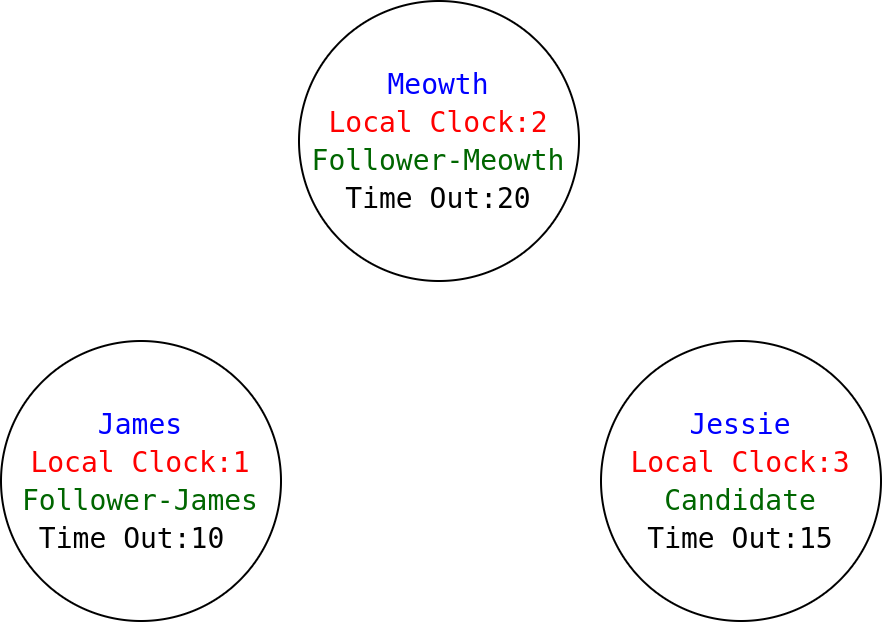
The idea is to describe the behavior of the raft leader election process using such functions
10
'tick'tick'tick'heartbeat'heartbeat
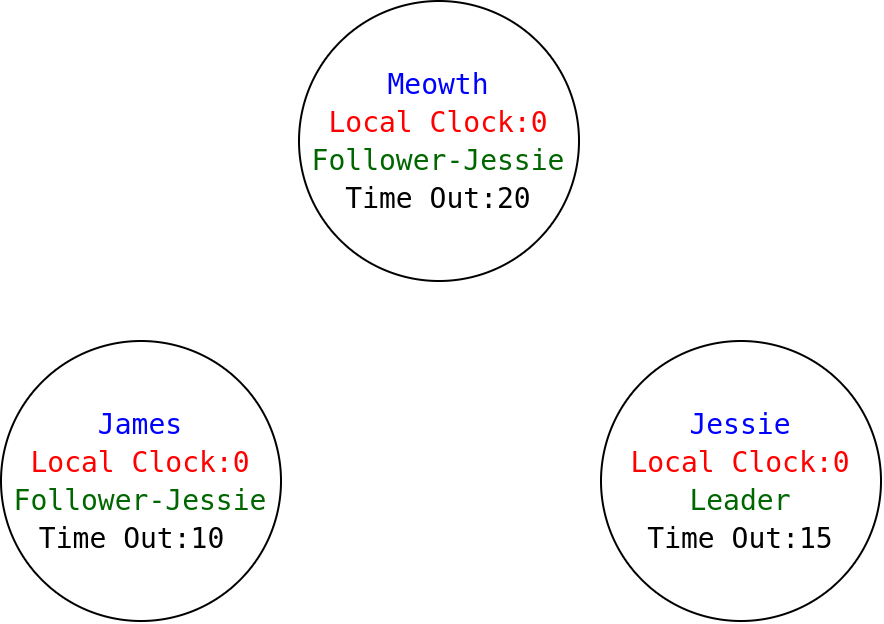
assert ready-to-definition :=
(fun [
(ls ready-to (send alias alias 'tick)) <==>
((ls=(Node (State nls (Local t0) fls0) (Name alias t1))) & (t0 < t1))
(ls ready-to (receive alias alias 'tick)) <==>
((ls=(Node (State nls (Local t0) fls0) (Name alias t1))) & (t0<t1))
])
assert next-definition :=
(fun[
(next (Node (State nls (Local t0) fls0) (Name alias t1)) (receive to fr c))=
[
(Node (State nls (Local S t0) fls0) (Name alias t1))
when
((t0<t1) & (to=fr) & (to=alias) & (c = 'tick) & (~nls = Leader))
(Node (State nls (Local zero) fls0) (Name alias t1))
when
((t0<t1) & (to=fr) & (to=alias) & (c='tick) & (nls=Leader))
]
])Defining the clock update behavior base on messages 'tick using the ready-to and next definition
11
When the internal clock of a node reaches its limit, various behavior are triggered within the system.
12
The safety invariant property for the clock limitsMain Result
Is crucial to ensure that the internal clock of a node never exceeds its specified limit

define raftls0 := (Node
(State Leader (Local t0) (Following alias0 v)) (Name alias1 t1))
define raftls1 := (next raftls0 (receive alias1 alias1 'tick))
define safety-name-limit-Leader :=
( forall t0 t1 v alias0 alias1 .
(t0 < t1)
==>
(focus-clock raftls1) <= (focus-limit raftls1)
)Athena’s assumption base endowed with the definitions/axioms about the election process, but there is no theorem about Raft’ behavior
13
Main Result
define raftls0 := (Node (State Leader (Local t0) (Following alias0 v)) (Name alias1 t1))
define raftls1 := (next raftls0 (receive alias1 alias1 'tick))
define safety-name-limit-Leader :=
( forall t0 t1 v alias0 alias1 .
(t0 < t1)
==>
(focus-clock raftls1) <= (focus-limit raftls1)
)
conclude safety-name-limit-Leader
pick-any t0 t1 v alias0 alias1
assume hyp := (t0 < t1)
(!chain<-
[
((focus-clock (next (Node (State Leader (Local t0) (Following alias0 v)) (Name alias1 t1)) (receive alias1 alias1 'tick))) <= (focus-limit (next (Node (State Leader (Local t0) (Following alias0 v)) (Name alias1 t1)) (receive alias1 alias1 'tick))))
<==
((focus-clock (Node (State Leader (Local zero) (Following alias0 v)) (Name alias1 t1)) ) <=
(focus-limit (Node (State Leader (Local zero) (Following alias0 v)) (Name alias1 t1))) )
[Node.next-definition]
<==
(zero <= t1)
[focus-RAFT-definition]
<==
true
]
)
define raftls2 := (Node (State Candidate (Local t0) (Following alias0 v)) (Name alias1 t1))
define raftls3 := (next raftls2 (receive alias1 alias1 'tick))
define safety-name-limit-Candidate :=
( forall t0 t1 v alias0 alias1 .
(t0 < t1)
==>
(focus-clock raftls3) <= (focus-limit raftls3)
)
conclude safety-name-limit-Candidate
pick-any t0 t1 v alias0 alias1
assume hyp := (t0 < t1)
(!chain<-
[
((focus-clock (next (Node (State Candidate (Local t0) (Following alias0 v)) (Name alias1 t1)) (receive alias1 alias1 'tick))) <= (focus-limit (next (Node (State Candidate (Local t0) (Following alias0 v)) (Name alias1 t1)) (receive alias1 alias1 'tick))))
<==
((focus-clock (Node (State Candidate (Local S t0) (Following alias0 v)) (Name alias1 t1)) ) <=
(focus-limit (Node (State Candidate (Local S t0) (Following alias0 v)) (Name alias1 t1))) )
[Node.next-definition]
<==
((S t0) <= t1)
[focus-RAFT-definition]
<==
(t0 < t1)
[N.Less=.discrete]
<==
true
]
)The is write within 70 line of Athena code further details could be found at:
https://gitlab.com/reasoning-about-actor-systems-ltl/Code
14
Future work
-
Log replication specification
-
Proof of raft key properties
- There is at most one leader in the configuration at any given moment.
-
Eventually the system will have only one leader in the configuration, per term.
-
Each replicated copy of the state machine executes the same commands in the same order.
15
Safety Verification of the Raft Leader Election Algorithm using Athena
By Mateo Sanabria Ardila
Safety Verification of the Raft Leader Election Algorithm using Athena
Safety Verification of the Raft Leader Election Algorithm using Athena
- 177



