UNIDAD IV
Programación Funcional
Profesor Miguel Cantillana


INS240 – Lenguajes de Programación
Ingeniería en Computación e Informática
Semestre 2017-1
Paradigma funcional con Python
Programación Funcional

¿Que significa funcional?

- Es un paradigma de programación que está basado en funciones.
- Se entiende el concepto de función según su definición matemática y no como simples subprogramas de los lenguajes imperativos.
- Funciones puras
- Las variables no tienen estado (Ausencia de estado): No hay cambios en éstas a lo largo del tiempo
- Inmutabilidad: No pueden cambiarse los valores a lo largo de la ejecución.
- Los programas se estructuran componiendo expresiones que se evalúan como funciones
Funciones puras e impuras

// Funcion Pura
function doble(num) {
return num * 2; // No modifica el argumento.
}
function doblarLista(listado){
// Retorna un nuevo listado sin modificar nada.
return listado.map(doble);
}
// Funcion Impura
function doblarLista(listado){
for( var i =0; i < listado.items; i++ ){
// Cambiamos los valores entregados como argumentos
listado[i] = doble(listado[i]);
}
}¿Por qué?

- Facilitar el testing.
- Reusabilidad.
- Depuración más fácil.
- Estado muy controlado.
¿Es python un lenguaje funcional?

- No.
- Es un lenguaje multi-paradigma.
- Soporta algunas caracterı́sticas funcionales.
- Permite hacer programación funcional.
- Carece de caracterı́sticas avanzadas presentes en lenguajes funcionales.
¿Que me dan los lenguajes funcionales?

- Estructuras inmutables eficientes.
- Funciones de orden superior.
- Pattern matching.
- TCO: Tail call optimization.
- Aplicación parcial y currificación.
- Control de efectos laterales.
- Funciones lambda.
- Evaluación perezosa.
- Composición de funciones.
¿Que nos entrega python?

- Funciones de primer orden.
- Funciones lambda.
- Funciones de orden superior.
- Evaluación perezosa (Limitada).
Tı́picas estrategias funcionales

- Combinación y composición de funciones pequeñas.
- Datos + funciones transformadoras.
- Aplicación de transformaciones mediante orden superior.
- Uso de funciones inline.
- Acotado de efectos laterales.
- Tendencia al uso de funciones puras.
Macrodiseño ⇒ Orientación a Objetos
Microdiseño ⇒ Programación Funcional
Funcional vs. Imperativo

Programación imperativa

- Unidad sintáctica elemental: la sentencia
- Operación elemental: la asignación
- Modelo: variables ... “computar”
import random as r
x = 1
y = r . randint (0 ,10)
if y % 2:
x = x + 3
else :
x = x - 2
print xProgramación funcional

- Unidad sintáctica elemental: la expresión
- Operación elemental: la aplicación
- Modelo: valores ... “calcular”
y = random . randint (0 , 10)
x = 1 + (3 if y % 2 else -2)
print xPython Funcional

Funciones de primer orden o de orden superior

- Genericidad: Las funciones pueden pasarse como parámetro.
- Instanciación: Las funciones pueden devolver otras funciones.
- Abstracción procedural: Cualquier sentencia puede convertirse en función.
-
Embebimiento: Las funciones pueden almacenerse en estructuras de datos.
Genericidad

-
Son funciones que reciben o devuelven funciones como parámetros.
-
Operan sobre funciones, es decir el dominio o la imagen de estas funciones son funciones.
Las funciones pueden pasarse como parámetro.
def ejecutarfun ( funcion ):
res = funcion ()
print " Resultado : " + str ( res )
ejecutarfun (random.random)Genericidad (ii)

Las funciones pueden pasarse como parámetro.
def superior(interna):
def funcion1():
print "Funcion1"
def funcion2():
print "Funcion2"
funcion = {
'uno' : funcion1,
'dos' : funcion2
}
return funcion[interna]
nueva_funcion = superior('dos')
nueva_funcion()Genericidad (iii)

Las funciones pueden pasarse como parámetro.
def funcion1():
print "Funcion1"
def funcion2():
print "Funcion2"
def superior(funcion):
funcion()
superior(funcion1)
superior(funcion2)Instanciación

Las funciones pueden devolver otras funciones.
def devuelvefun ( param ):
if param : return random.random
else : return list
fun = devuelvefun ( True )
print fun ()
fun = devuelvefun ( False )
print fun ()Abstracción procedural

Cualquier sentencia puede convertirse en función.
def make_sumador ( k ):
def sumador ( x ):
return x + k
return sumador
mas_dos = make_sumador (2)
print mas_dos (1) # Imprime 3
print mas_dos (2) # Imprime 4# Ejemplo (Abstracción + Instanciación)
Abstracción procedural ... Lambdas

lambda <parámetros>:<expresión></expresión></parámetros>
Son funciones anónimas, mínimas definidas en una línea, no pueden contener bucles y no pueden utilizar la palabra clave return para regresar un valor.
- Lambda = Función anónima (sin nombre).
- ¡Sólo expresiones!
Abstracción procedural ... Lambdas

cuadrado = lambda x: x ** 2
print cuadrado(2)
lista = range(10)
for numero in lista:
print cuadrado(numero)Abstracción procedural ... Lambdas

def make_sumador_lambda ( k ):
return lambda x : x + k
mas_dos = make_sumador_lambda (2)
print mas_dos (1)
print mas_dos (2)Embebimiento

Cualquier función puede guardarse en cualquier parte.
from operator import add , sub , div # , mul
funcs = {
'+' : add ,
'-' : sub ,
'*' : lambda a , b : a * b ,
'/' : div
}
print funcs ['+'] (1 , 2)
print funcs ['-'] (1 , 2)
print funcs ['*'] (1 , 2)
print funcs ['/'] (1 , 2)Funciones de alto orden

Filosofı́a
Trabajar sobre listas ⇒ Abstraer la iteración
- map (func, lista): Devuelve una lista aplicando func a cada elemento
- reduce (func, lista, (primero)): Devuelve un valor aplicando la operación binaria func
- filter (pred, lista): Devuelve una lista filtrando con el predicado pred
map (func, lista)

Aplica una función sobre cada ítem de una lista y devuelve una lista donde se le aplicó la función a cada elemento
nueva_lista = map(función, lista)
lista = [0,1,2,4,5,6,7,8,9]
lista_nueva = map(lambda x: x**2, lista)
print lista_nuevareduce (func, lista, (primero))

reduce los ítems de una lista aplicando una función reductora, devuelve un solo valor
valor = reduce(función, lista, (primero))
lista = [0,1,2,4,5,6,7,8,9]
sumatoria = reduce(lambda x, y: x+y, lista)
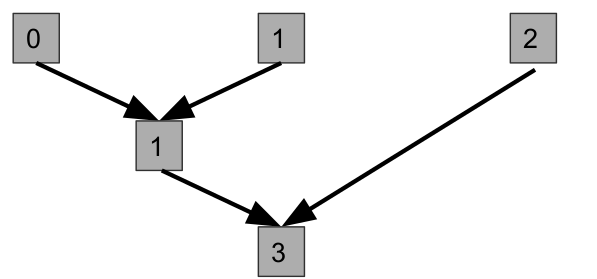
print sumatoriareduce (func, lista, (primero))

reduce los ítems de una lista aplicando una función reductora, devuelve un solo valor
valor = reduce(función, lista)
filter (pred, lista)

coteja que los elementos de una lista cumplan con cierta condición expresada en una función boolean.
nueva_lista = filter(funcion, lista)
lista = [0,1,2,4,5,6,7,8,9]
pares = filter(lambda x: x % 2 == 0, lista)
print paresOtras utilidades

Emparejar los elementos de dos listas ...
zip ( 'hola' , range (3))Verdadero si todos son verdaderos ...
all ([ True , [] , True ])Verdadero si alguno es verdadero ...
any ([ True , [] , True ])Listas por comprensión

Es una construcción compacta que permite mapear y/o filtrar una lista en otra aplicando una función a cada elemento de la lista, opcionalmente la lista original puede ser filtrada
Crear una lista con los cuadrados de los dígitos:
print [digito**2 for digito in range(10)] Crear una lista con los cuadrados de los digitos pares
print [digito**2 for digito in range(10) if digito % 2 == 0] Ejercicios en clases

Ejercicio 1
Escriba una función de orden superior que permita ejecutar una función n veces, donde n y la función debes ser argumentos.
Ejercicio 2
Implemente las funciones map, filter y reduce por sus propias manos.
Ejercicios en clases

Ejercicio 3
Sin utilizar bucles, implemente una función que reciba dos listas y devuelva otra lista con los productos de cada par de números.
Ejercicio 4
Realice el ejercicio anterior (Ejercicio 5), utilizando listas por comprensión.
Recursos

- http://librosweb.es/libro/algoritmos_python/capitulo_10/mutabilidad_e_inmutabilidad.html
- https://www.genbetadev.com/paradigmas-de-programacion/programacion-funcional-un-enfoque-diferente-a-los-problemas-de-siempre
UNAB: LP14
By Miguel Cantillana
UNAB: LP14
Clase 14
- 775



