ENCRYPTION

Part 2:
Secret Key Exchange (Diffie-Hellman)

How to share a secret key without actually "saying" it

When you submit a password or credit card number online, your computer has to send that data to another computer over the internet.

Any data sent over the internet can be seen by anyone else, so computers are instructed to scramble (encrypt) sensitive data with a secret key before sending it out.

The receiving computer needs to know that secret key in order to unscramble (decrypt) the data.

So how do they communicate the secret key??

STEP 1

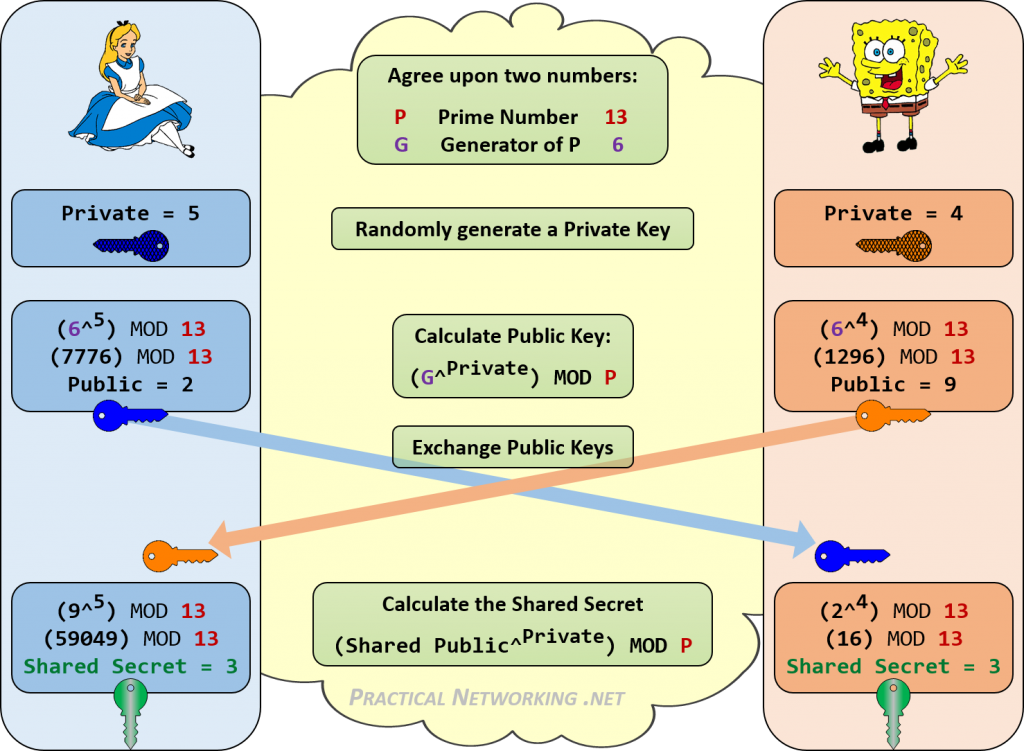
Alice sends Bob 2 numbers:

• a random "base" number

• a large PRIME number

This happens in public

STEP 2

Alice and Bob each choose a private key that they will never share with each other.

This happens in secret

STEP 3

Alice and Bob each calculate a public key using this formula:

base ** mySecret  %  prime

This happens in secret

STEP 4

They exchange their newly created public keys

This happens in public

STEP 5

They each repeat the formula, this time replacing the base with each other's public key

Alice does this:

bobPublic ** aliceSecret  %  prime

Bob does this:

alicePublic ** bobSecret  %  prime

They end up with the SAME number – their SHARED SECRET KEY

...without ever exposing it

Things to know:

• The modulo operation acts as a one-way function. There's no pattern to reverse engineer it.

• When you multiply big numbers and mod them by other big numbers, it’s really hard to figure out what the original numbers were; the technique is essentially reduced to random guessing, which would take an unreasonable amount of time.
   

• In 2015, computer scientists discovered the Logjam attack, a security vulnerability against Diffie–Hellman key exchanges that use 512-bit to 1024-bit keys. This is avoided by using prime numbers that are 2048-bit or larger.

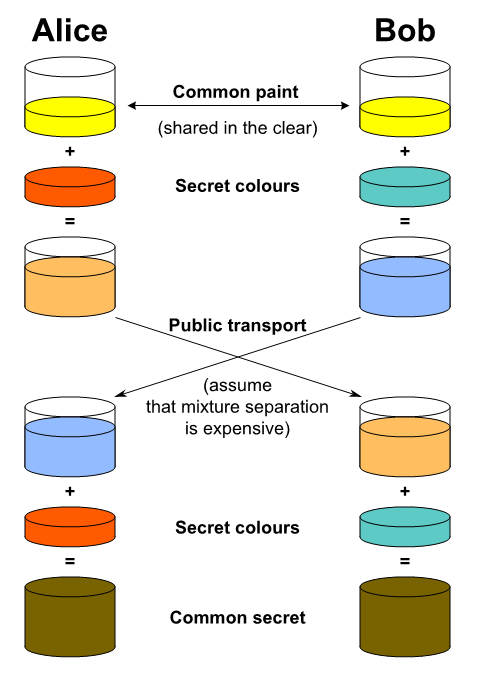
It’s like mixing paint - very computationally hard (expensive) to figure out the exact shade of the secret color that was added.

Interactive Demo