Kepler's Laws
Gravity and Satellites
Kepler's Laws of Planetary Motion
Kepler's Laws of Planetary Motion
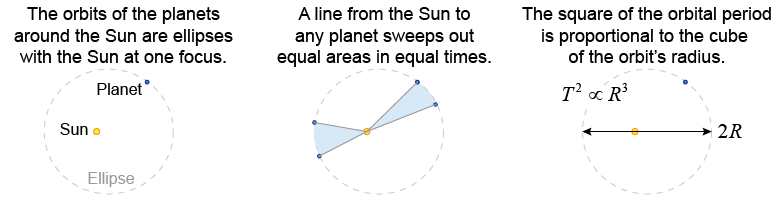
1st Law
2nd Law
3rd Law
Kepler used Tycho Brahe's detailed observations of planets to find 3 empirical laws
\mathrm{(Orbital \ Period)}^2 = \mathrm{(Semi \ Major \ Axis)}^3
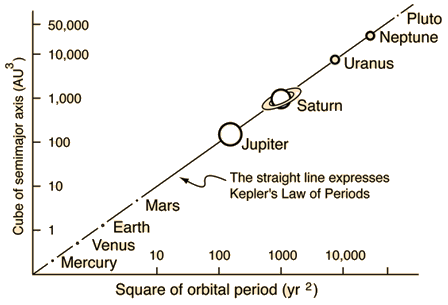
The square of the orbital period is proportional to the cube of the average distance.
Kepler's Laws of Planetary Motion
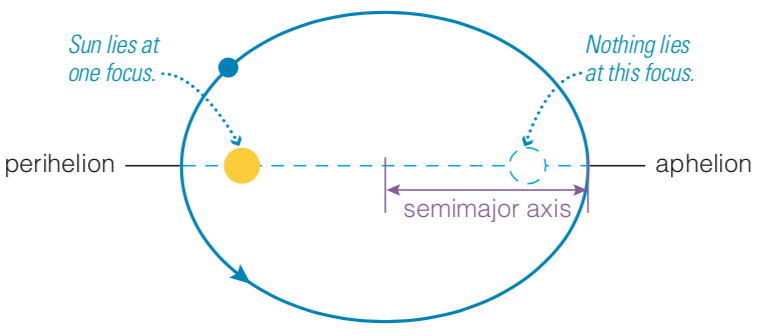
Kepler’s first law: The orbit of each planet about the Sun is an ellipse with the Sun at one focus
"near the sun"
"away from the sun"
Properties of Ellipses
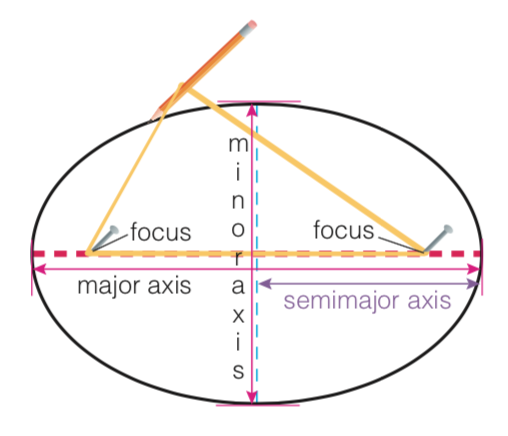
a
b
a + b = major axis
Properties of Ellipses
\mathrm{eccentricity} = \mathrm{\frac{distance \ from \ foci \ to \ center}{semi \ major \ axis}} = \mathrm{\frac{distance \ between \ foci}{major \ axis}}
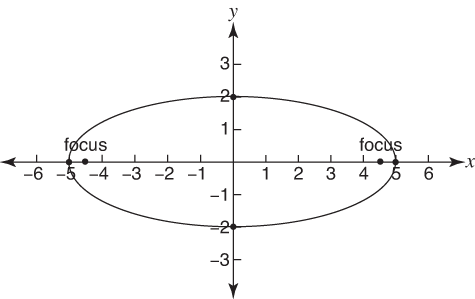
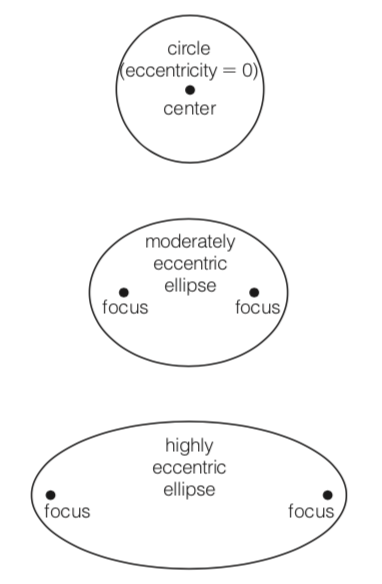
Checkpoint
What is the eccentricity of the following ellipse?
4.5/5 or 9/10 = 0.9
\mathrm{eccentricity} = \mathrm{\frac{distance \ from \ foci \ to \ center}{semi \ major \ axis}} = \mathrm{\frac{distance \ between \ foci}{major \ axis}}
Kepler's Laws of Planetary Motion
Kepler’s second law: A planet moves faster in the part of its orbit nearer the Sun and slower when farther from the Sun, sweeping out equal areas in equal times.
Kepler's Laws of Planetary Motion
Kepler’s second law: A planet moves faster in the part of its orbit nearer the Sun and slower when farther from the Sun, sweeping out equal areas in equal times.
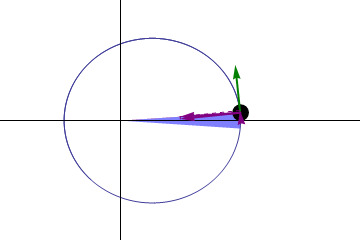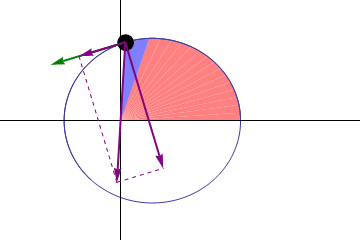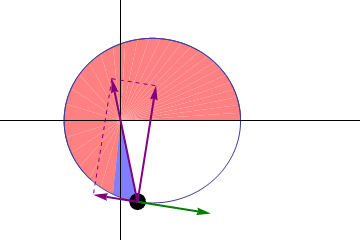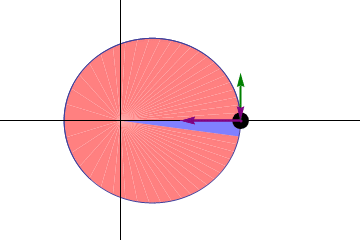
This implies that planets move faster at perihelion
Checkpoint
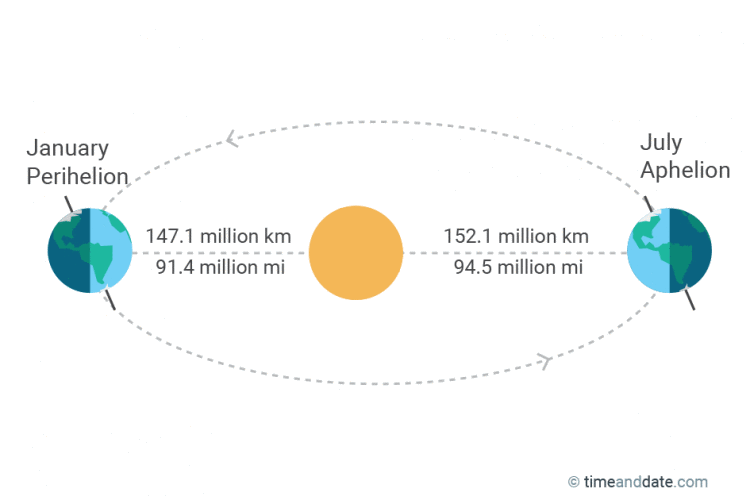
Earth's perihelion is on January while its aphelion is on July. Because of this the winters in the northern hemisphere are ____________ than the winters in the southern hemisphere.
Kepler's Laws of Planetary Motion
Kepler’s third law: More distant planets orbit the Sun at slower average speeds, obeying the following mathematical relationship
\mathrm{(Orbital \ Period)}^2 = \mathrm{(Semi \ Major \ Axis)}^3
p^2 = a^3 => p = \sqrt{a^3}
a = p^{2/3}
Where
a = Semi Major Axis and p = Orbital Period
Kepler's Laws of Planetary Motion
Kepler’s third law: More distant planets orbit the Sun at slower average speeds, obeying the following mathematical relationship
Kepler's Laws of Planetary Motion
Gravity
Is the force pulling an apple down the tree the same as the one keeping the moon around the Earth?
Isaac Newton under an apple tree at his mother's house
1665-1667
Newton's Mountain:
If you throw a stone horizontally fast enough, the stone keeps falling, but it never reaches the ground (because of the curvature of the Earth)
The Universal Law of Gravity
Is the force pulling an apple down the tree the same as the one keeping the moon around the Earth?
The Universal Law of Gravity
Is the force pulling an apple down the tree the same keeping the moon around the Earth?
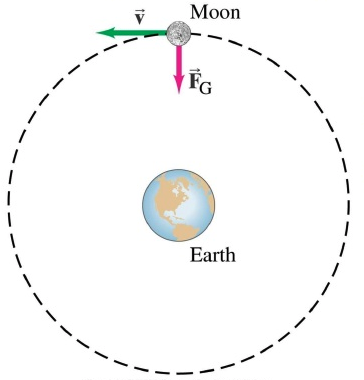
Yes it is!
Is the force of gravity
The Universal Law of Gravity
Is the force pulling an apple down the tree the same as the one keeping the moon around the Earth?
Force of Gravity
The force of gravity must be proportional to the product of the mass of the two objects interacting (i.e. M1*M2)
M1
M1
M2
M2
M1
M1
The Universal Law of Gravity
The force of gravity is inversely proportional to the square of the distance
\mathrm{F_G} \propto \frac{1}{\mathrm{distance^2}}
This is because intensity spreads over the surface area of a sphere
The Universal Law of Gravity
\mathrm{F_G} \propto \frac{1}{\mathrm{distance^2}}
This is because intensity spreads over the surface area of a sphere
The force of gravity is inversely proportional to the square of the distance
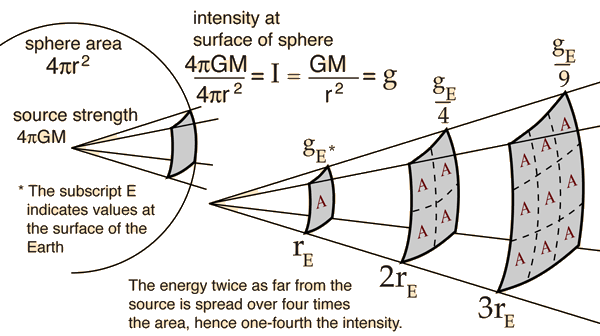
The Universal Law of Gravity
\mathrm{F_G} \propto \frac{\mathrm{mass_1}\times\mathrm{mass_2}}{\mathrm{distance^2}}
\mathrm{F_G} = G \frac{m_1m_2}{d^2}
The force of gravity is proportional to the product of the mass of the objects and inversely proportional the square of the distance
G = 6.67 \times 10^{-11} \mathrm{\frac{N \ m^2}{kg^2}}
Checkpoint
An apple weighs 1 N at Earth's surface. How much does it weighs when it is 4 times as far?
4 R
\mathrm{F_G} = \frac{1}{\mathrm{4^2}}\mathrm{N} = \frac{1}{\mathrm{16}}\mathrm{N}
Kepler's Laws of Planetary Motion
Kepler's Laws were finally explained when Newton formulated his Law of Gravitation. They naturally arise as the force of gravity decreases with distance^2
Mass v.s. Weight
Mass vs. Weight
Mass and weight are not the same
Mass is a property of objects due to how much matter they have
Weight is the gravitational force objects experience due to gravity
Weight
Weight is the gravitational force objects experience due to gravity. Weight is proportional to the mass of objects, but is not the same as mass!
Weightlessness
(a.k.a. Zero Gravity)
Weightlessness
Being weightless does not mean there is no gravity, what it means is that there is no support force (free falling)
Weightlessness
Without a support force you experience weightlessness, but that doesn't mean there is zero gravity
Without a support force you experience weightlessness, but that doesn't mean there is zero gravity
Weightlessness/Zero Gravity
Speed, Velocity and Acceleration
Velocity vs. Speed
Velocity is a Vector - magnitude and direction
Speed is a Scalar - magnitude
\mathrm{Speed} = \frac{\mathrm{distance}}{\mathrm{time}}
\mathrm{Velocity} = \frac{\mathrm{distance}}{\mathrm{time}}
In a specific direction
Vectors vs. Scalars
Vectors - magnitude and direction
Scalars - magnitude
Examples:
Force
Acceleration
Velocity
Examples:
Mass
Volume
Speed
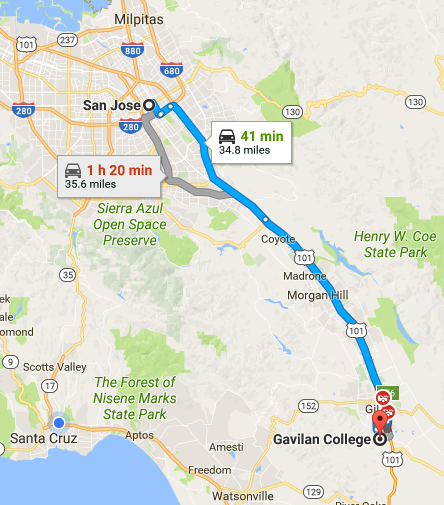
Checkpoint
What was your average speed if you commuted from San Jose to Gavilan (35 miles) in 35 min
\mathrm{Average \ Speed} = \frac{35 \ \mathrm{miles}}{35 \ \mathrm{minutes}}
= 1 \frac{\mathrm{miles}}{\mathrm{min}}[\frac{60 \ \mathrm{min}}{\mathrm{hour}}] = 60 \frac{\mathrm{miles}}{\mathrm{hour}}
What about your average velocity?
= 60 \frac{\mathrm{miles}}{\mathrm{hour}} \ \mathrm{SE}
\mathrm{Average \ Speed} = \frac{\mathrm{Total \ distance \ covered}}{\mathrm{Time \ interval}}
Acceleration
\mathrm{Acceleration} = \frac{\mathrm{Chance \ of \ velocity}}{\mathrm{Time \ interval}} = \frac{\Delta \ v}{\Delta \ t}
Checkpoint
If a car goes from rest to 36 km/h in 10s, what is its acceleration?
\mathrm{Acceleration} = \frac{\Delta \ v}{\Delta \ t} = \frac{ 36 \ \mathrm{km/h}}{10 \ \mathrm{s}} = 3.6 \frac{ \mathrm{km}}{\mathrm{h \cdot s}}[\frac{1 \ \mathrm{h}}{3600 \ \mathrm{s}}]
= 1\times 10^{-3} \frac{ \mathrm{km}}{\mathrm{s}^2}
\mathrm{Acceleration} = \frac{\mathrm{Chance \ of \ velocity}}{\mathrm{Time \ interval}} = \frac{\Delta \ v}{\Delta \ t}
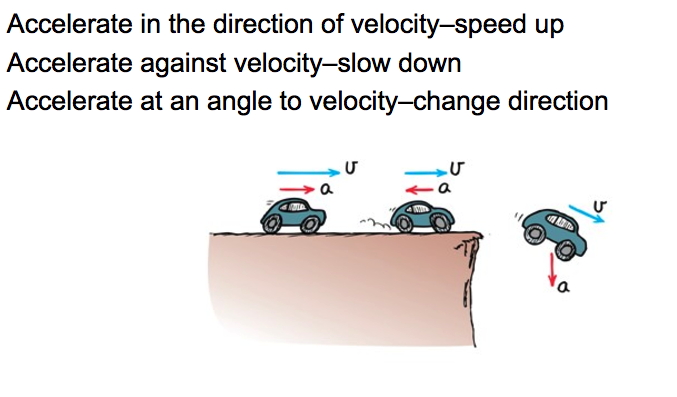
Acceleration is a vector!
Checkpoint
If the Moon travels around the Earth at a constant speed of 1 km/s, is it accelerating?
Newton's Laws Of Motion
My Short Summary of Newton's Laws
For every action there is a reaction: To every action there is always an opposed equal reaction.
a = \frac{F}{m}
Summary of Newton's Laws
1st - Law of Inertia: Every object continues in a state of rest or uniform speed in a straight line unless acted on by a nonzero net force.
2nd - Acceleration is caused by a not zero net force: The acceleration of an object is directly proportional to the net force acting on a object, is in the direction of the net force, and inversely proportional to the mass of the object.
3rd - For every action there is a reaction: To every action there is always an opposed equal reaction.
a = \frac{F}{m}
Newtons 2nd Law
Acceleration is inversely proportional to mass
\mathrm{Acceleration} \propto \frac{\mathrm{1}}{\mathrm{mass}}
\mathrm{Acceleration} = \frac{\mathrm{Net \ Force}}{\mathrm{mass}}
Free falling objects experience the same acceleration regardless their mass
This is because:
\mathrm{Force \ of \ gravity} \propto \mathrm{mass}
a = \frac{F_g}{m} = G \frac{M m}{m d^2} = G \frac{M}{d^2}
On the surface of Earth,
a = g = 9.8 m/s^2
for all objects!
\mathrm{acceleration} \propto \frac{1}{\mathrm{mass}}
Constant Acceleraton
Free Fall
\Rightarrow v = a \ t
From rest ( )
v_i = 0
d = \frac{a}{2} \ t^2
Set
t_i = d_i = 0
a = g = 9.8 \ \frac{m}{s^2}
Checkpoint
How far down (distance) would you fall in 1 second after you base jump from a cliff. Ignore air resistance.
d = \frac{a}{2} \ t^2
a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}
,
v = a \ t
d = \frac{a}{2} \ t^2
,
| t (s) | v (m/s) | d (m) |
|---|---|---|
| 0 | ||
| 2 | ||
| 4 | ||
| 6 | ||
| 8 | ||
| 10 |
| 0 | 0 |
|---|---|
| 20 | 20 |
| 40 | 80 |
| 60 | 180 |
| 80 | 320 |
| 100 | 500 |
a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}
Free Fall Motion
d = \frac{a}{2}t^2 \Rightarrow d \propto t^2
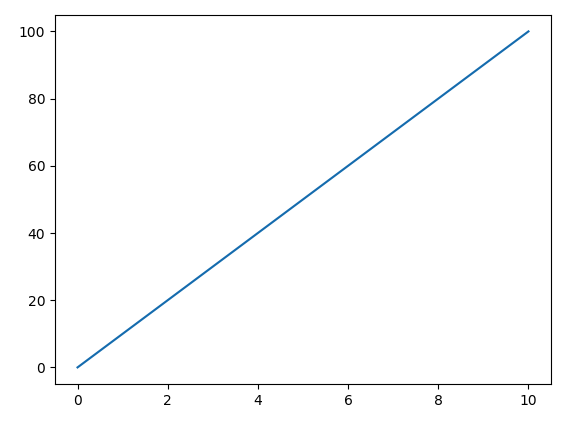
Constant Acceleration
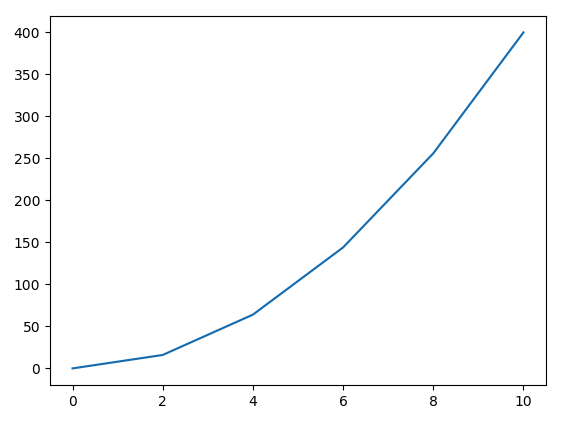
velocity
distance
Time
Time
v = a \ t \Rightarrow v \propto t
Constant Acceleration
velocity (m/s)
Time (s)
v = a \ t \Rightarrow v \propto t
If acceleration is the slope of the velocity vs. time plot how do you find the acceleration given the plot?
a = \mathrm{slope}
a = \mathrm{slope} = \frac{\mathrm{rise}}{\mathrm{run}} = \frac{100\frac{m}{s}}{10 s} = 10\frac{m}{s^2}
Satellites
Checkpoint
How far down (distance) would you fall in 1 second after you base jump from a cliff. Ignore air resistance.
d = 5 meters after 1 second
d = \frac{a}{2} \ t^2
a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}
,
v = a \ t
How fast would you be falling?
Vertical velocity = 10 m/s
v = a \ t
d = \frac{a}{2} \ t^2
,
a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}
d = 5 meters after 1 second
5m in 1s
If a projectile falls 5m in 1s,
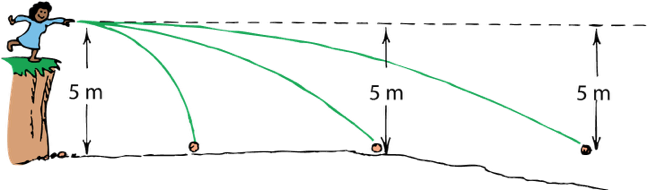
and the curvature of earth is so that it drops 5m for every 8km
What happen if you throw a rock with an horizontal velocity of 8000 m/s = 8 km/s (18,000 mi/h)?
Satellites
Satellites
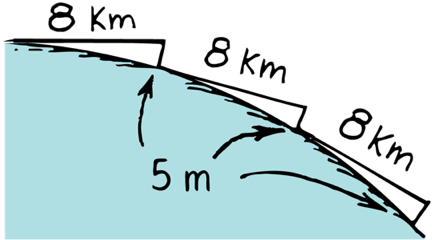
Satellites
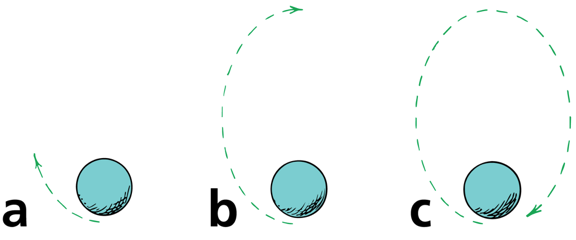
A satellite moves in an elliptical orbit
a) When the satellite exceeds 8 km/s, it overshoots a circle. b) At its maximum separation, it starts to come back toward Earth.
c) The cycle repeats itself.
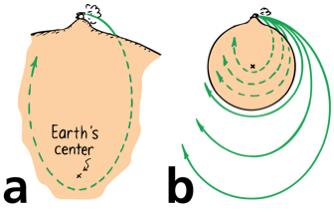
Satellites
a) A projectile's path is a section of an elliptical orbit
b) a satellite moves in an elliptical orbit
Scape Velocity
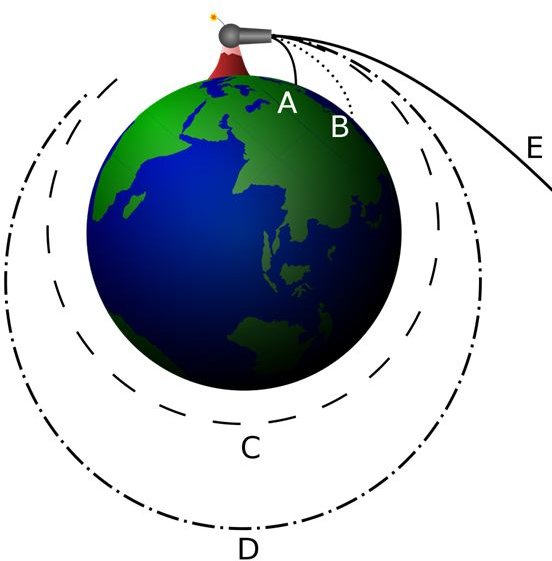
Neglecting air resistance if you throw a rock with a velocity greater than 11.2 Km/s (25000 miles/h), it wont come back
The Universal Law of Gravity
\mathrm{F_G} \propto \frac{\mathrm{mass_1}\times\mathrm{mass_2}}{\mathrm{distance^2}}
\mathrm{F_G} = G \frac{m_1m_2}{d^2}
The force of gravity is proportional to the product of the mass of the objects and inversely proportional the square of the distance
G = 6.67 \times 10^{-11} \mathrm{\frac{N \ m^2}{kg^2}}
The Universal Law of Gravity
The force of gravity is inversely proportional to the square of the distance
\mathrm{F_G} \propto \frac{1}{\mathrm{distance^2}}
This is because intensity spreads over the surface area of a sphere
Checkpoint
Your weight would be 2^2 = 4 times greater
If the radius of the earth became 1/2 of what it is now, how would your weight change?
\mathrm{F_G} \propto \frac{1}{\mathrm{distance^2}}
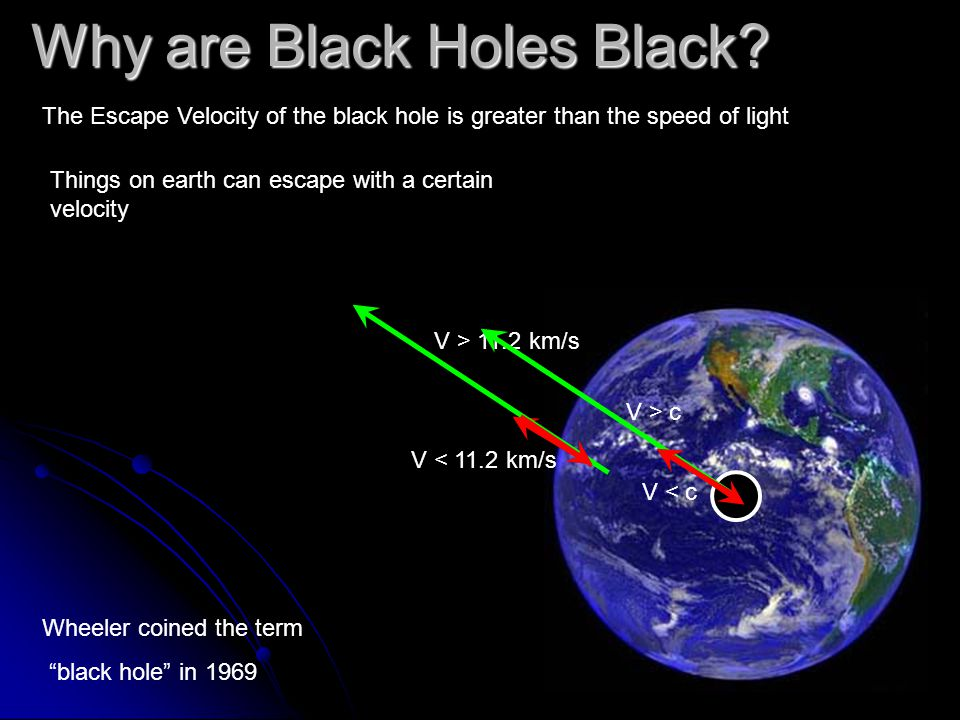
Black Holes
At the surface of a black hole the force of gravity is so strong that not even light has enough velocity to scape
Black Holes
At the surface of a black hole the force of gravity is so strong that not even light has enough velocity to scape
Black Hole Formation
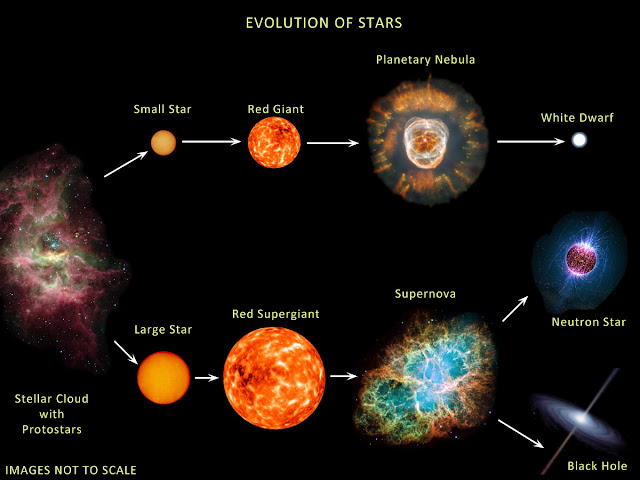
Only stars with a mass > ~1.5x the mass of the sun become black holes
Neutron starts can pack up ~1.4x the mass of the sun on a radius that is the size of a city
In order to achieve such a high density they combine electrons and protons to form neutrons
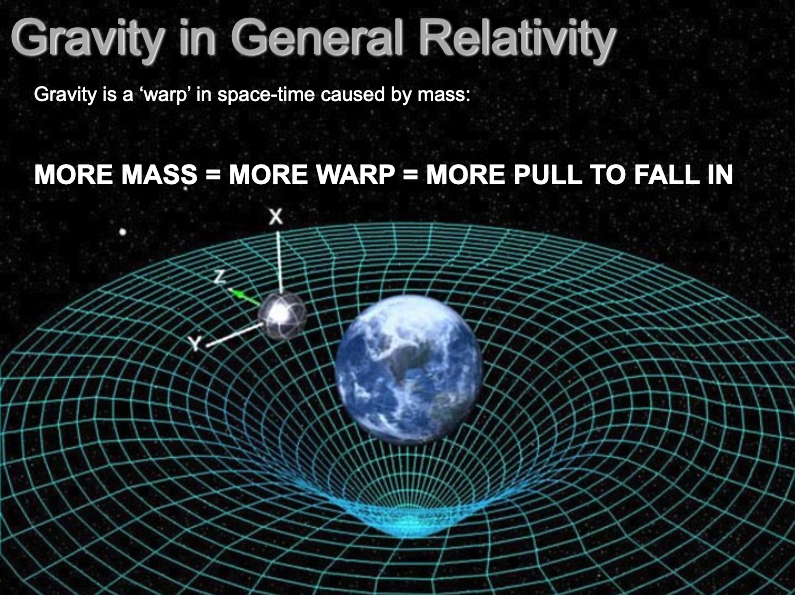
Newtonian Gravity v.s. Einstein's General Relativity
Einstein's
Gravity is the curvature of space and time due to Energy. Massless objects such as light can experience gravity
V.S.
Newton's
Gravity is a force field surrounding massive objects. Other masses interact with this force field
Gravitational Waves
First observed in 2015
The End
Energy Conservation on Satellites
On a circular orbit the force does not work and the PE and KE remain constant
On an elliptical orbit the force does some work and the PE and KE vary, however KE + PE is conserverd
Mass vs. Weight
1. Pull slowly on the string -- what happens?
2. Pull quickly on the string -- what happens?
Isaac Newton
1642 - 1726
Isaac Newton was an English mathematician, astronomer, and physicist (described in his own day as a "natural philosopher") who is widely recognized as one of the most influential scientists of all time and a key figure in the scientific revolution. His book Philosophiæ Naturalis Principia Mathematica ("Mathematical Principles of Natural Philosophy"), first published in 1687, laid the foundations of classical mechanics. Newton also made pathbreaking contributions to optics, and he shares credit with Gottfried Wilhelm Leibniz for developing the infinitesimal calculus.
Newton's First Law of Motion
Newton refined Galileo's idea of inertia and made it his first law, appropriately called the law of inertia
Every object continues in a state of rest or of uniform speed in a straight line unless acted on by a nonzero net force.
Newtons 2nd Law
Forces cause acceleration
Inetertia resists acceleration
and
\mathrm{Acceleration} = \frac{\mathrm{Net \ Force}}{\mathrm{mass}}
\mathrm{Acceleration} \propto \mathrm{Net \ Force}
\mathrm{Acceleration} \propto \frac{1}{\mathrm{mass}}
Newtons 3rd Law
To every action there is always an opposed equal reaction
Whenever an object exerts a force on a second object, the second object exerts an equal an opposite force to the first
Or in other words
Newtons 3rd Law: For every action there is a reaction
Force is the same, acceleration is different
acceleration is what causes the damage
Action and reaction of different masses
M
m
a = \frac{F}{m}
Black Holes
The size of the sun is the result of a “tug of war” between two opposing processes: nuclear fusion (pressure) and gravitational contraction
If the fusion rate increases, the sun will get hotter and bigger. If the fusion rate decreases, the sun will get cooler and smaller
Black Holes
When the sun runs out of fusion fuel (hydrogen), gravitation will dominate and the sun will start to collapse
Black Hole Formation
Only stars with a mass > ~1.5x the mass of the sun become black holes
Kepler's Laws, Gravity and Satellites
By Miguel Rocha
Kepler's Laws, Gravity and Satellites
Astro 1 - Kepler's Laws, Gravity and Satellites Slides
