Ideal Gases
M. Rocha
Physics 2A
Pressure
Pressure is force per unit area
\mathrm{Pressure} = \mathrm{\frac{Force}{Area}}
Metric unit of pressure is Pascal.
1 Pascal = 1 Newtons per square meter
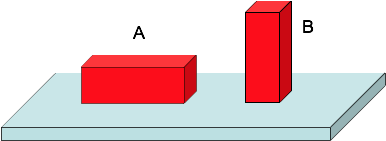
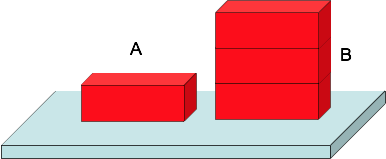
A pressure < B pressure
A pressure < B pressure
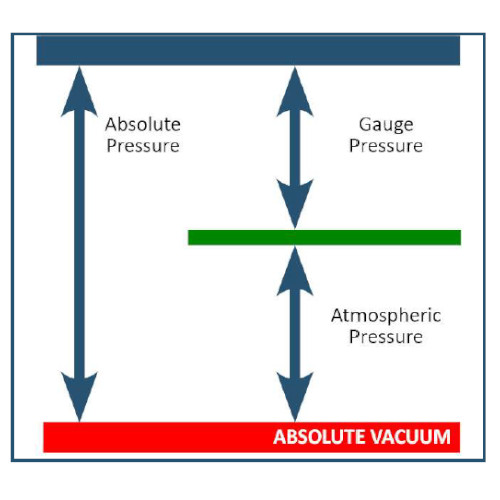
Gauge Pressure
P_{abs} = P_g + P_{atm}
P_g = P_{abs} - P_{atm}
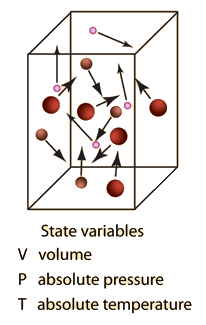
Ideal Gas Definition
An ideal gas is defined as one in which all collisions between atoms or molecules are perfectly elastic and in which there are no intermolecular attractive forces. One can visualize it as a collection of perfectly hard spheres which collide but which otherwise do not interact with each other. In such a gas, all the internal energy is in the form of kinetic energy and any change in internal energy is accompanied by a change in temperature.
Temperature and Kinetic Energy
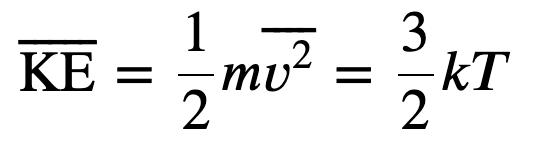
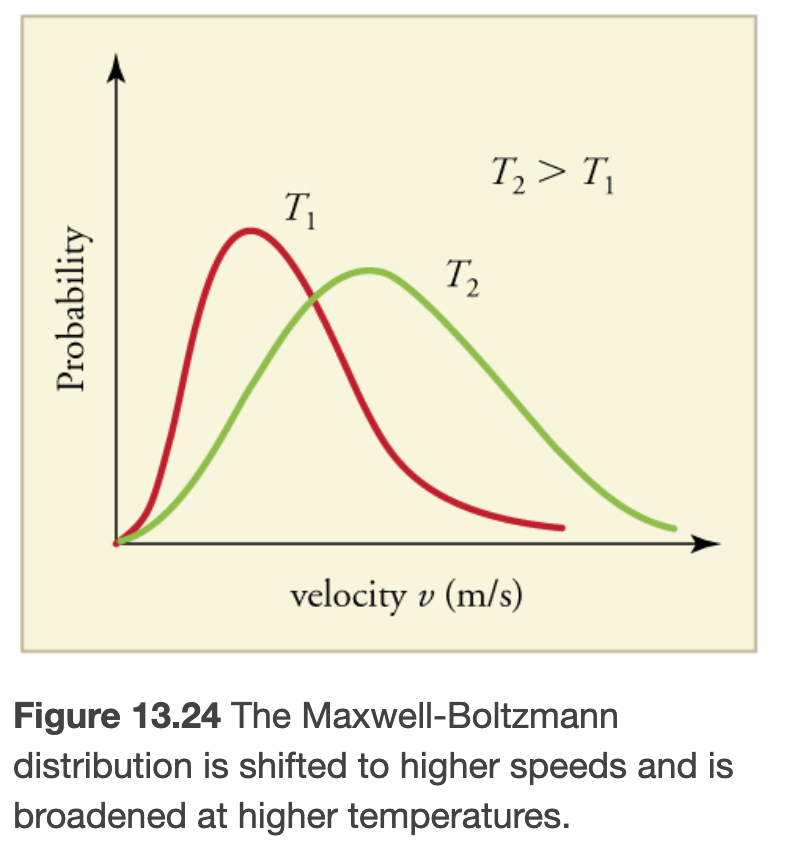
The average translational kinetic energy of molecules in an ideal gas is related to its temperature by the thermal energy equation
Where k is the boltzmann constant
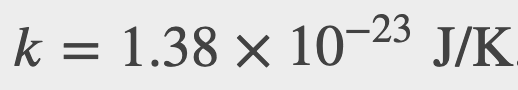
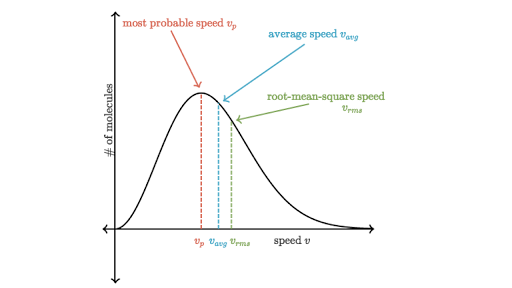
(a) What is the average kinetic energy of a gas molecule at 20.0ºC (room temperature)? (b) Find the rms speed of a nitrogen molecule (N_2) at this temperature.
Checkpoint
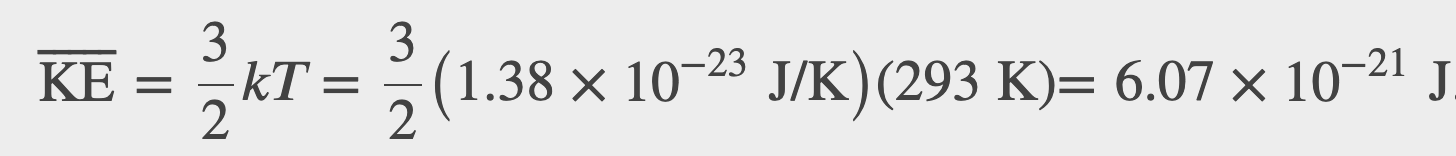
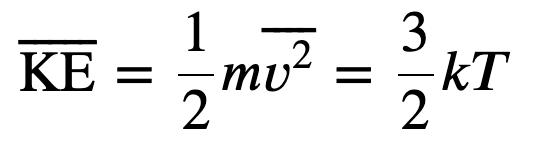
The Ideal Gas Law
Remember Boyle's Law
When the volume of a gas is decreased, the density increases and therfore pressure increases
P_iV_i = P_fV_f
PV = \mathrm{constant}
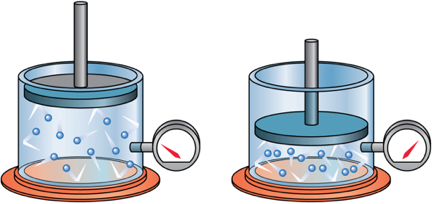
Boyle's Law is a conservation of energy equation, for cases where the internal energy is constant.
PV = \mathrm{Energy}
PV = \frac{F}{A}Ad = Fd = \mathrm{Work}
PV = N kT
PV = \frac{2}{3}N \overline{KE}
For ideal gases the internal energy is all due to temperature, i.e. the thermal energy of all molecules in the contained gas
Where N is the number of atoms/molecules in the gas, and the factor of 2/3 is introduced by relating the mechanical energy due to PV to the avg. kinetic energy of a molecules. Finally using the thermal energy equation we can get the ideal gas law
The ideal gas law, relates Pressure and Volume with Temperature/Thermal Energy
PV = N kT
The Ideal Gas Law
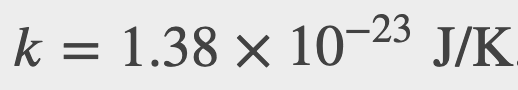
Where N is the number of atoms/molecules in the gas and
You may also find it useful in units of moles
PV = n RT
Where n is the number of moles in the gas and
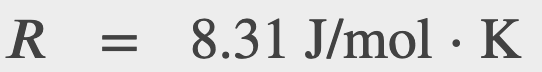
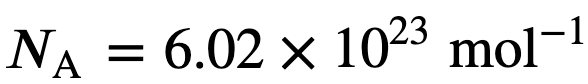
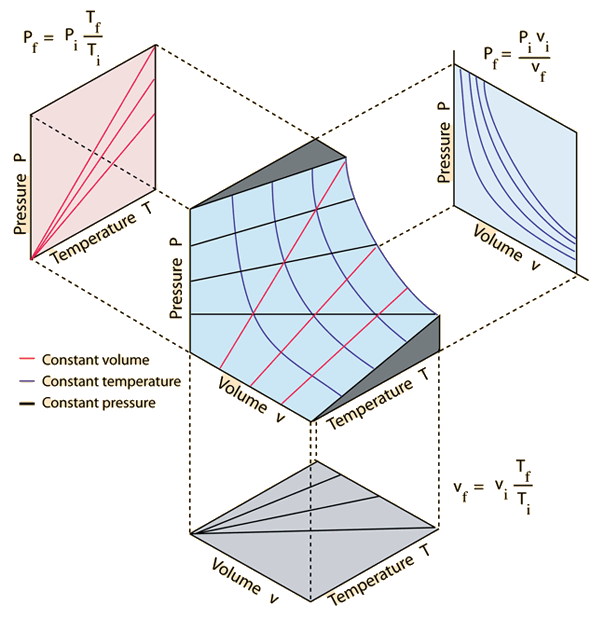
The ideal gas law, relates Pressure and Volume with Temperature
Boyle's Law
Suppose your bicycle tire is fully inflated, with an absolute pressure of 7.00×10^5 Pa (90.0lb/in^2) at a temperature of 18.0ºC. What is the pressure after its temperature has risen to 35.0ºC ? Assume that there are no appreciable leaks or changes in volume.
Checkpoint
PV = N kT
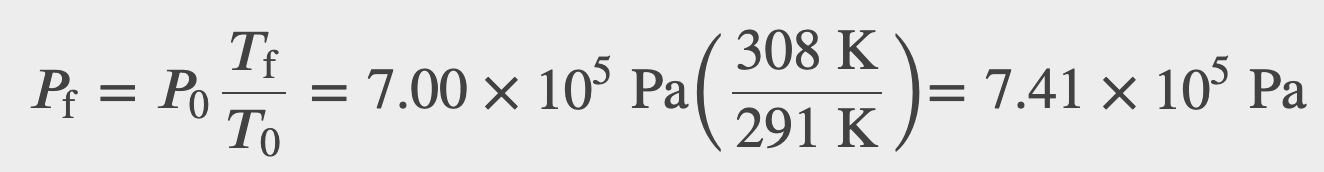
The density of air at standard conditions (𝑃 =1 atm and 𝑇=20ºC) is 1.28 kg/m^3. At what pressure is the density 0.64 kg/m^3 if the temperature and number of molecules are kept constant?
Checkpoint
P_f = 0.5 \ atm
PV = N kT
Ideal Gases
By Miguel Rocha
