Fluids Continued
M. Rocha
Physics 2A
Pressure
Pressure is force per unit area
\mathrm{Pressure} = \mathrm{\frac{Force}{Area}}
Metric unit of pressure is Pascal.
1 Pascal = 1 Newtons per square meter
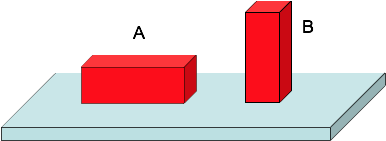
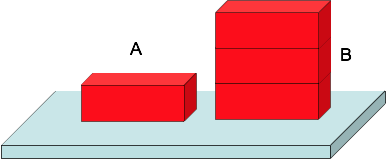
A pressure < B pressure
A pressure < B pressure
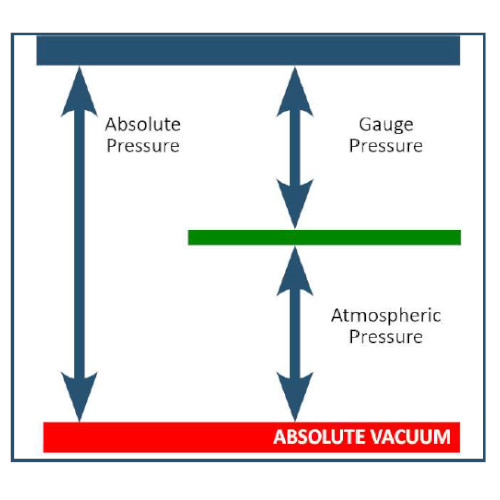
Gauge Pressure
P_{abs} = P_g + P_{atm}
P_g = P_{abs} - P_{atm}
Pressure in Fluids is Independent of Area
P = \frac{F}{A} = \frac{mg}{A}
m = \rho V = \rho Ah
\Rightarrow P = \frac{(\rho A h )g}{A} = \rho h g
Checkpoint
Intravenous infusions are usually made with the help of the gravitational force. Assuming that the density of the fluid being administered is 1.00 g/ml, at what height should the IV bag be placed above the entry point so that the fluid just enters the vein if the blood pressure in the vein is 18 mm Hg above atmospheric pressure?
P = \rho h g
h = \frac{P}{\rho g}
h = 0.24 m
Pascal's Priciple
Changes in pressure at any point in an enclosed fluid at rest are transmitted undiminished to all points in the fluid
Pascal's Priciple
Changes in pressure at any point in an enclosed fluid at rest are transmitted undiminished to all points in the fluid
\Rightarrow \frac{F_1}{A_1} = \frac{F_2}{A_2}
P_1 = P_2
Pascal's Priciple
Checkpoint
\frac{F_1}{A_1} = \frac{F_2}{A_2}
Pascal's Principle Demonstration
Checkpoint
50m
R = 0.25m
Calculate the force inside the barrel due to the water pressure. For simplicity assume that the barrel is a perfect cylinder.
P = \rho h g = \frac{F}{A}
Fluid Dynamics
Flow Rate
Flow Rate is constant
Checkpoint
The aorta is the principal blood vessel through which blood leaves the heart in order to circulate around the body. (a) Calculate the average speed of the blood in the aorta if the flow rate is 5.0 L/min. The aorta has a radius of 10 mm. (b) Blood also flows through smaller blood vessels known as capillaries. When the rate of blood flow in the aorta is 5.0 L/min, the speed of blood in the capillaries is about 0.33 mm/s. Given that the average diameter of a capillary is 8.0𝜇m, calculate the number of capillaries in the blood circulatory system.
\tilde{v} = 0.27 \ m/s
n_{\mathrm{capillaries}} = 5 \times 10^9
Bernoulli's Principle
When the speed of a fluid increases the pressure in the fluid decreases.
Bernoulli's Principle
When the speed of a fluid increases the pressure in the fluid decreases.
This phenomenon is due to energy conservation; when fluid’s kinetic energy increases (velocity increases) its internal potential energy (pressure) decreases
1
1
2
2
Checkpoint
An airplane has a mass 1200 kg and a wing area of 20 m^2. The wind speed at the top surface of the wings is 80 m/s and the wind speed at the bottom surface is 65 m/s. What is the lift force acting on the plane?
F_L = F_1 - F_2 = 33600 \ N
F_{net} = F_L - W = 2(33600) - 12000 = 55200 \ N
The End
Fluids and Fluid Dynamics
By Miguel Rocha
