Relativity
M. Rocha
Relativity is the study of how different observers measure the same event. Galileo and Newton developed the first correct version of classical relativity. Einstein developed the modern theory of relativity.
Galileo
Newton
Einstein
Classical Relativity
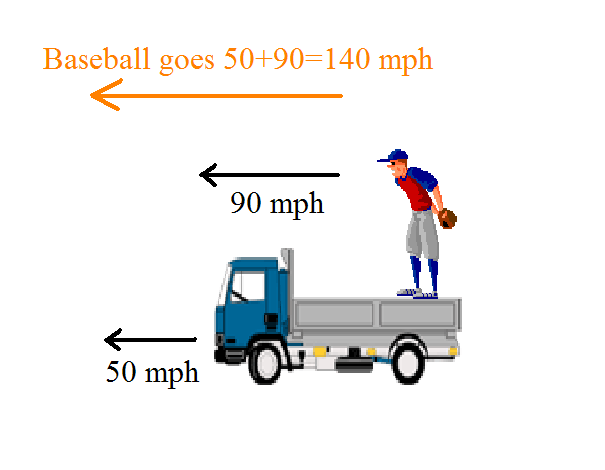
Relativity in physics is a method for two observers moving relative to each other to agree on what they are observing
In classical relativity you just add the velocities, in this case of the moving frame (truck) and the baseball
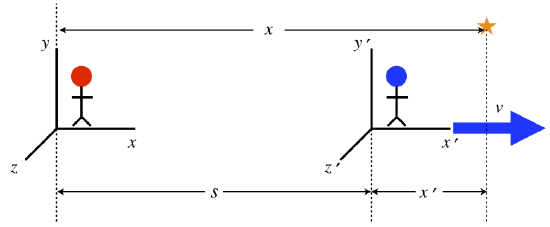
Inertial Reference Frames
All velocities are measured relative to some frame of reference.
An inertial frame of reference is a reference frame in which a body at rest remains at rest and a body in motion moves at a constant speed in a straight line unless acted on by an outside force.
Rotating and accelerating frames are NOT inertial frames
Modern Relativity
- Special Relativity:
- General Relativity:
Special relativity deals with observers who are moving at constant velocity.
Inertial Frames
General relativity deals with observers who are undergoing acceleration.
Non-Inertial Frames
Einstein's Special Relativity
In 1905, Einstein postulated 2 things:
- The laws of physics are the same and can be stated in their simplest form in all inertial frames of reference.
- Thus the speed of light (a fundamental physics constant) must be the same for all observers independent on their relative motions.
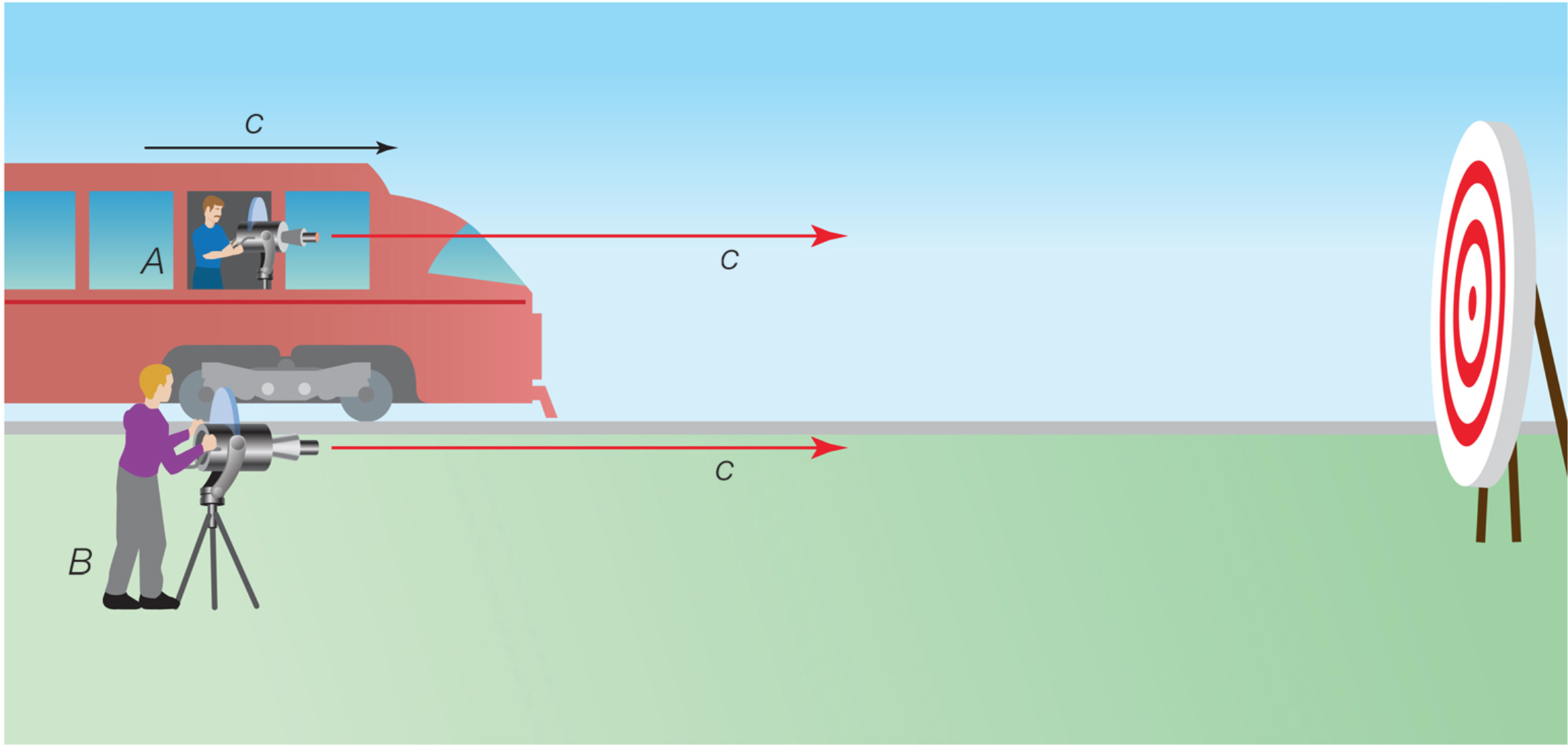
The Michelson-Morley experiment (1887) implied that the speed of light 𝑐 is independent of the motion of the source relative to the observer.
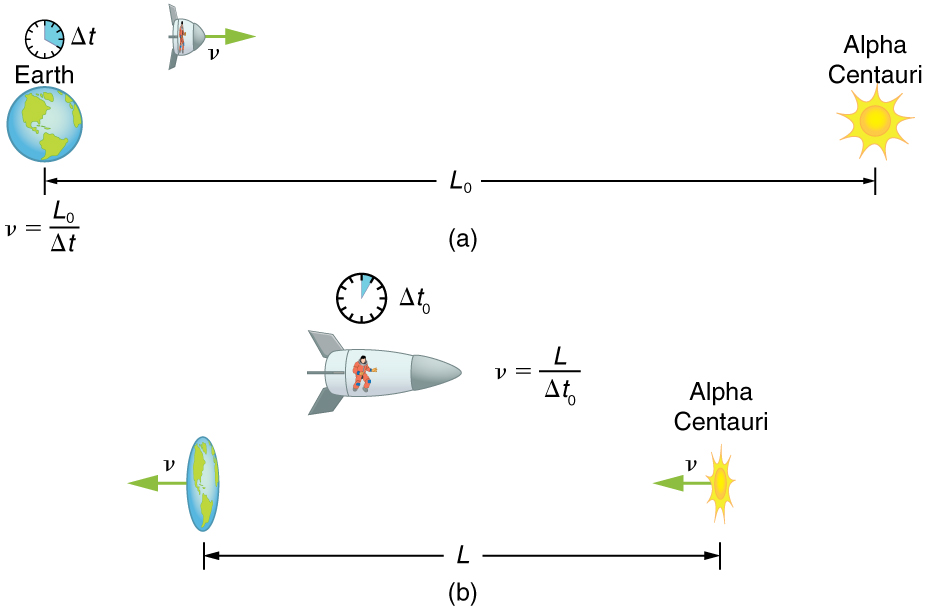
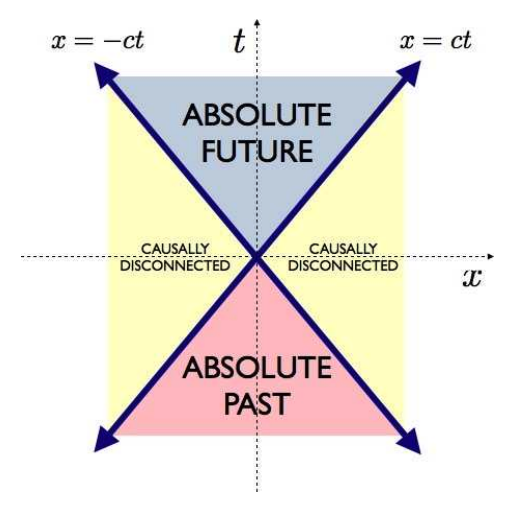
Space-Time in Relativity
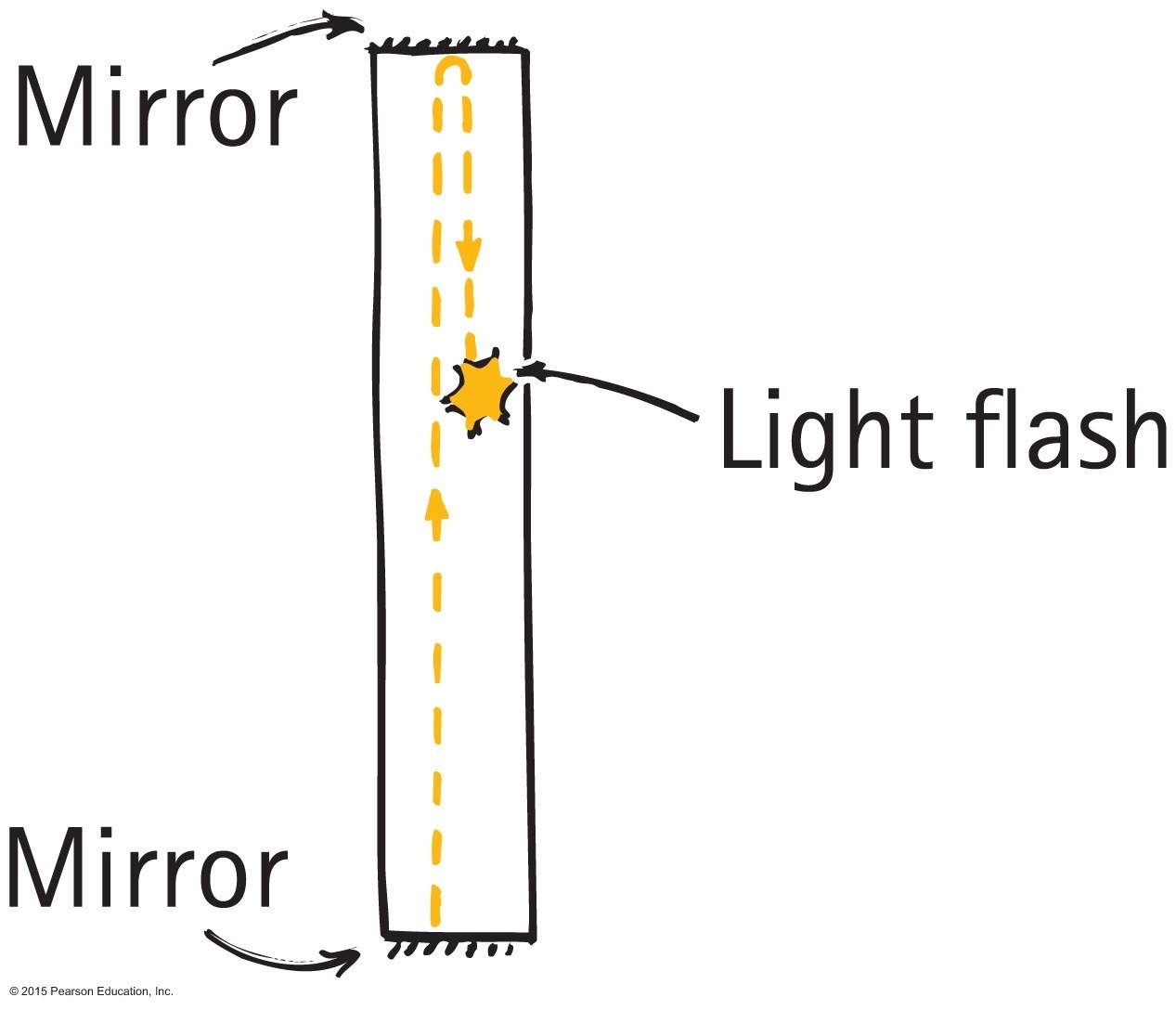
If the speed of light is constant for all observers regardless of their velocity, the distance and time must be different
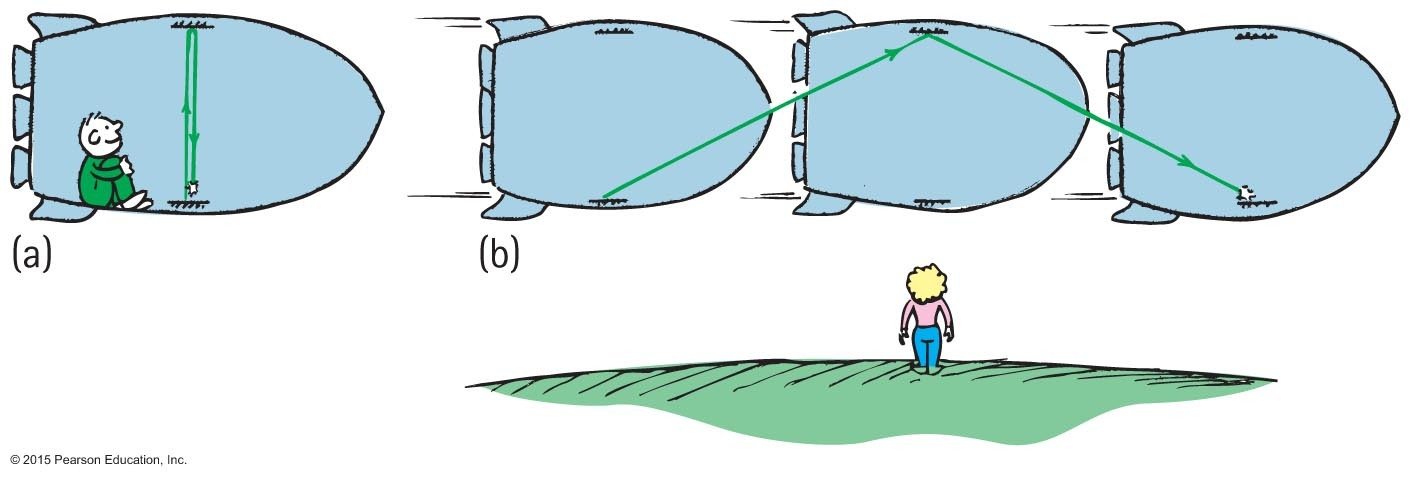
(a)
(b)
Time Dilation
Time dilation is the phenomenon of time passing slower for an observer who is moving relative to another observer.
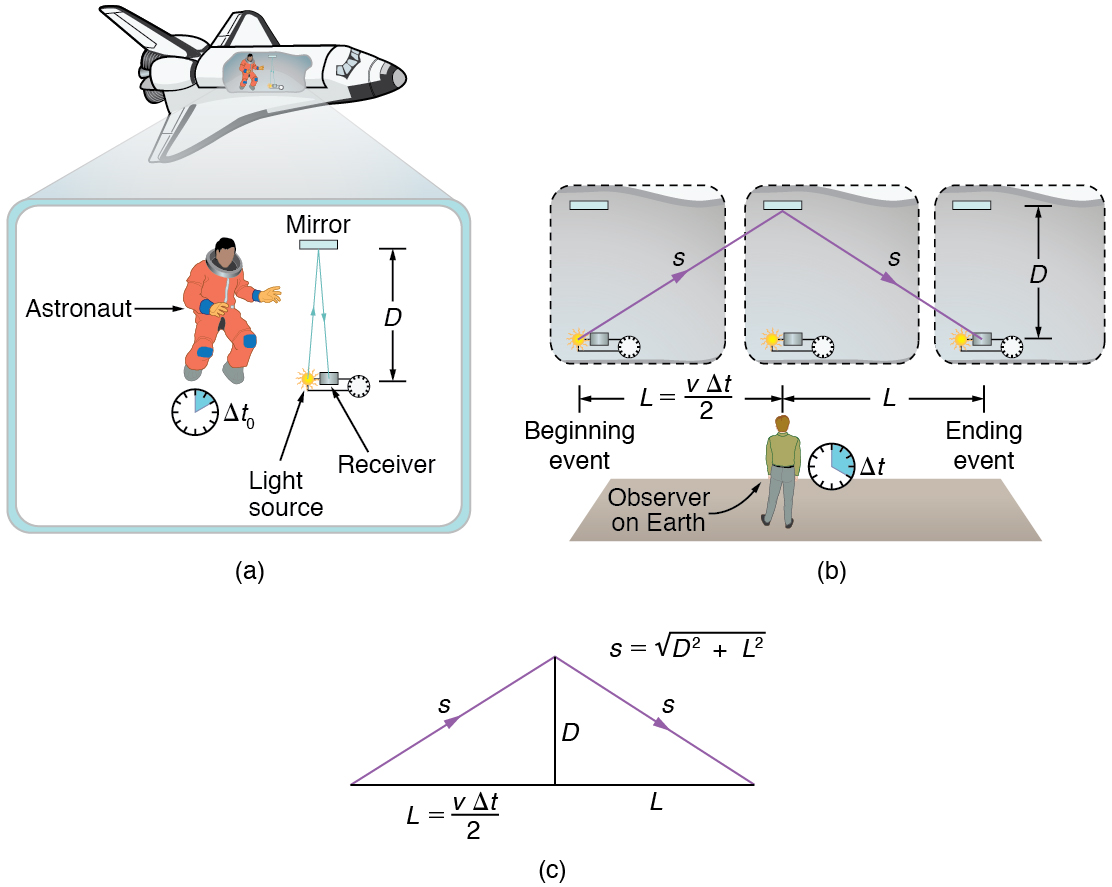
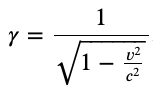
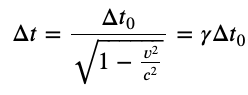
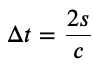
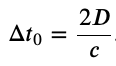
*Proper time is the time measured by an observer at rest relative to the event being observed.
where
s^2 = D^2 +L^2
Proper time*
The Lorentz Factor 𝛾
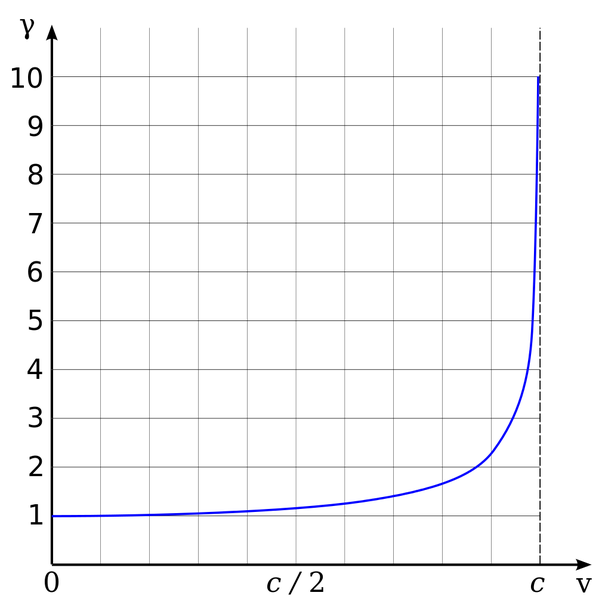
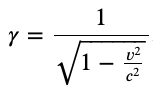
When
𝑣 << 𝑐: 𝛾 -> 1
𝑣 -> 𝑐: 𝛾 -> ∞
Checkpoint
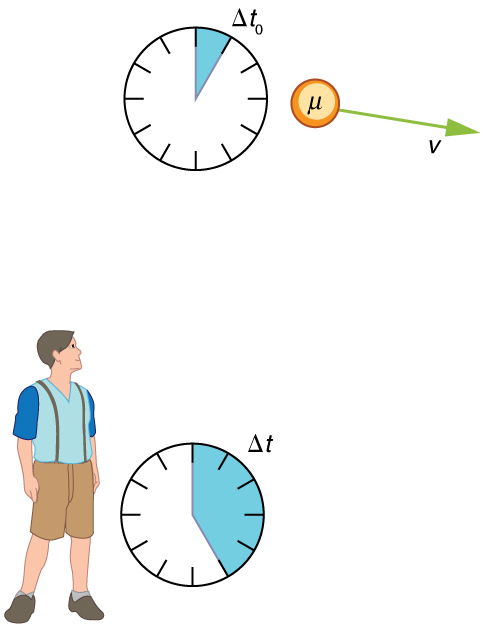
Suppose a cosmic ray colliding with a nucleus in the Earth’s upper atmosphere produces a muon that has a velocity 𝑣 = 0.95𝑐. The muon then travels at constant velocity and lives 1.52𝜇s as measured in the muon’s frame of reference. (You can imagine this as the muon’s internal clock.) How long does the muon live as measured by an Earth-bound observer?
v/c = 0.95 \Rightarrow \gamma = \frac{1}{\sqrt{1 - 0.95^2}} = 3.2
\Delta t = \gamma \Delta t_0 = (3.2) (1.52) \mu s = 4.87 \mu s
The Twin Paradox
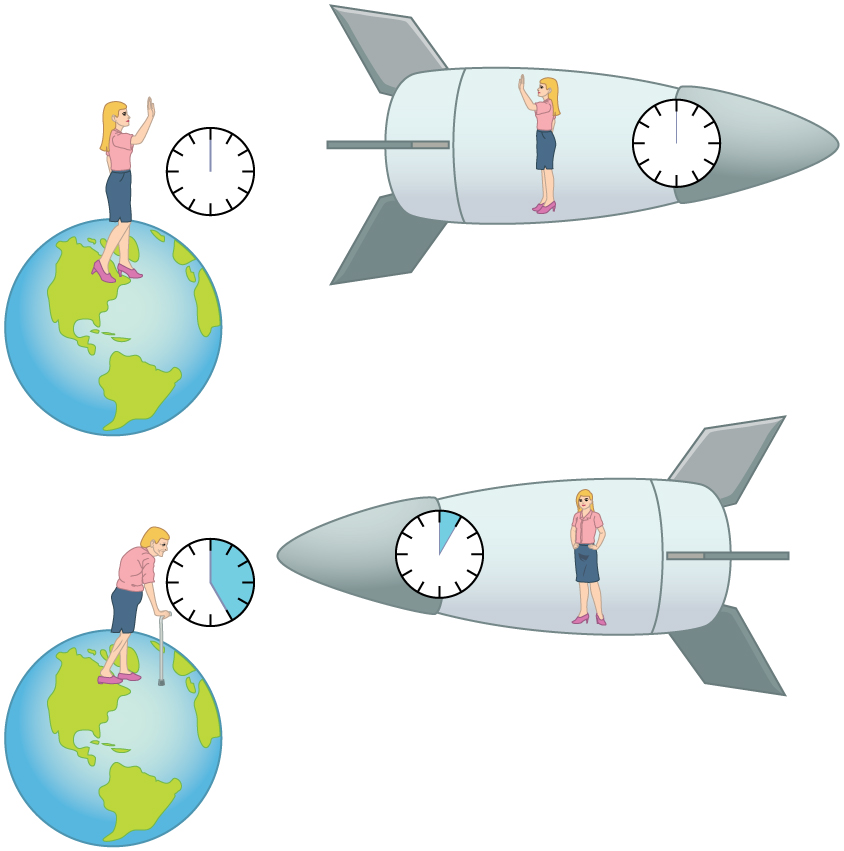
The twin paradox asks why the traveling twin ages less than the Earth-bound twin. That is the prediction we obtain if we consider the Earth-bound twin’s frame. In the astronaut’s frame, however, the Earth is moving and time runs slower there. Who is correct?
To resolve the paradox you need General Relativity
Length Contraction
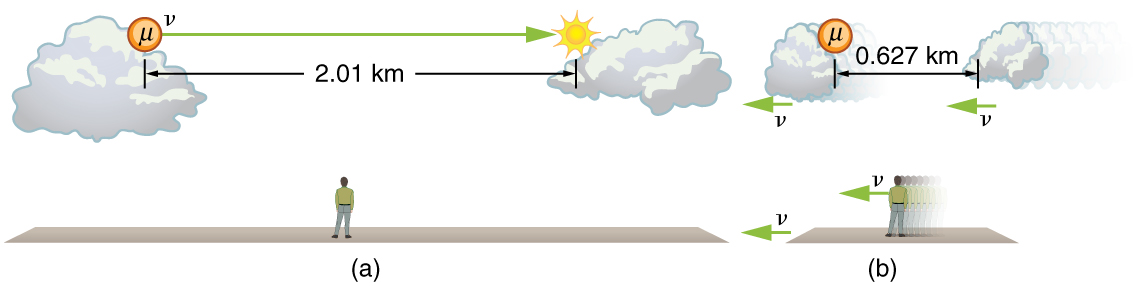
Length contraction is the shortening of the measured length of an object moving relative to the observer’s frame.
Proper length is the distance between two points measured by an observer who is at rest relative to both of the points.
=
\Rightarrow
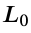
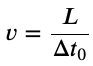
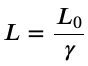
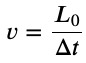
Checkpoint
Suppose an astronaut travels so fast that 𝛾 = 30. (a) She travels from the Earth to the nearest star system, Alpha Centauri, 4.3 light years away as measured by an Earth-bound observer. How far apart are the Earth and Alpha Centauri as measured by the astronaut?
L = \frac{L_0}{\gamma} = \frac{4.3 \ ly}{30} \\
= 0.143 \ ly
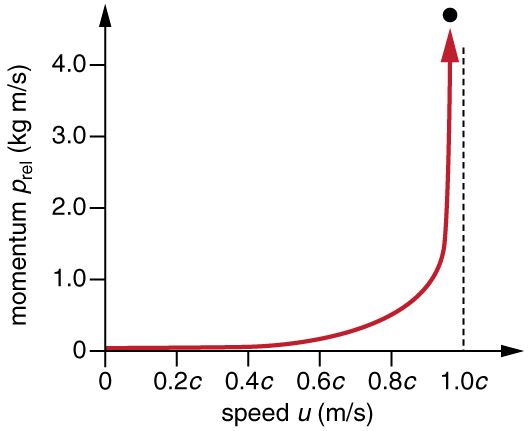
Relativistic Momentum
Relativistic momentum 𝑝 is the classical momentum multiplied by the relativistic factor 𝛾
p = \gamma m u
where 𝑚 is the rest mass of the object, 𝑢 is its velocity relative to an observer
Relativistic Energy
Einstein showed that the law of conservation of energy is valid relativistically, if we define energy to include the relativistic factor 𝛾
E = \gamma m c^2
where 𝑚 is the rest mass of the object and c is the speed of light
Total Energy:
Rest Energy:
E_0 = m c^2
Kinetic Energy:
KE_{rel} = (\gamma - 1) m c^2
v = 0,
\gamma = 1
E^2 = (pc)^2 + (mc^2)^2
Relativistic Energy In Terms of Momentum
Relativistically, we can obtain a relationship between energy and momentum by algebraically manipulating their definitions. This produces
where 𝐸 is the relativistic total energy and 𝑝 is the relativistic momentum.
Special Relativistic Addition of Velocities and Doppler Shift
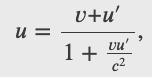
where 𝑣 is the relative velocity between two observers, 𝑢 is the velocity of an object relative to one observer, and 𝑢′ is the velocity relative to the other observer.
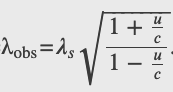
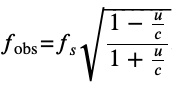
Where 𝜆_obs is the observed wavelength, 𝜆_𝑠 is the source wavelength, and 𝑢 is the relative velocity of the source to the observer.
Space Time in Modern Relativity
Space Interval
ds^2 = c dt^2 - dx^2
ds = 0
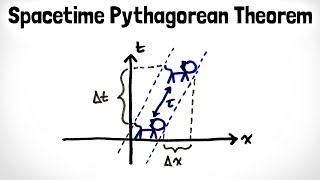
For anything traveling at the speed of light
Space-Time in Relativity
General Relativity
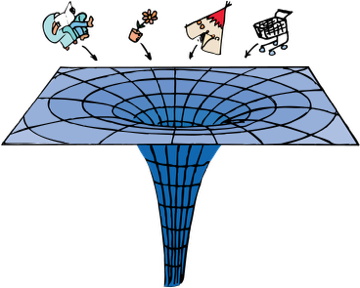
Einstein's
Gravity is the curvature of space and time due to massive objects
V.S.
Newton's
Gravity is a force field surrounding massive objects. Other masses interact with this force field
Einstein extended his theory of relativity to accelerating frames. This lead to the postulate that gravity is the curvature of space-time
ds^2 = (1 - \frac{2GM}{c^2r})(c dt^2 - dx^2)
Gravitational Lensing
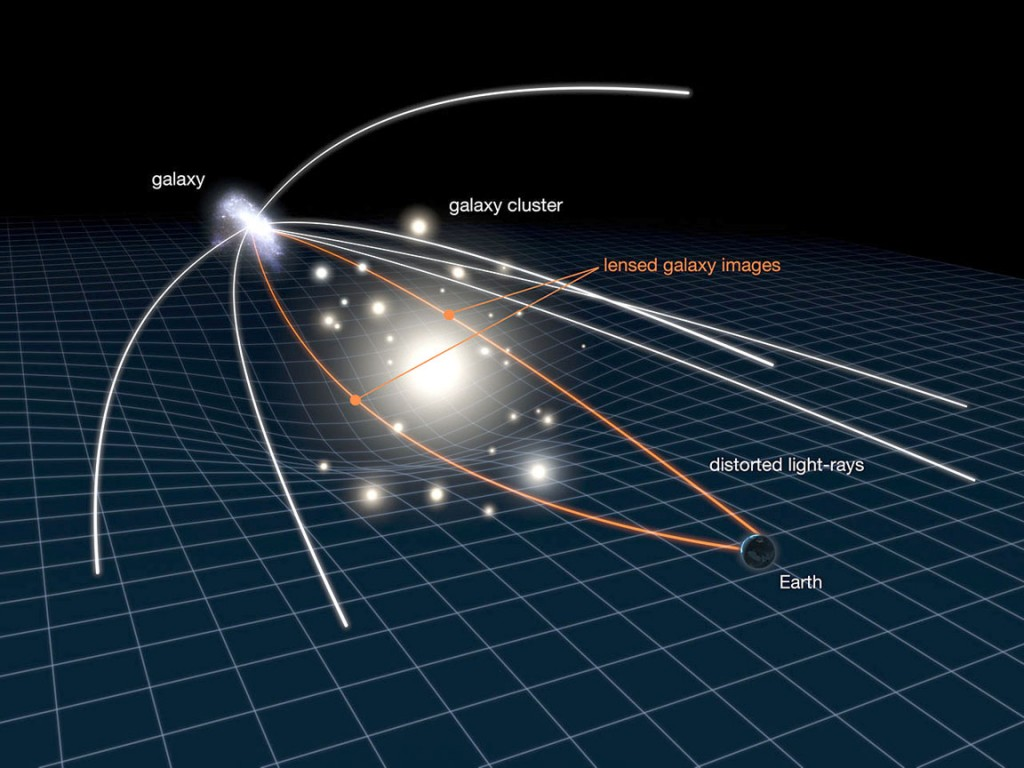
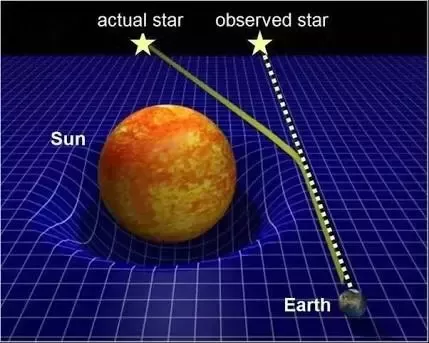
Gravitational lensing is evidence of the curvature of space-time. Light has no mass, in order to experience gravity massive objects must curve space and time
Gravitational Waves
First observed in 2015
Relativity
By Miguel Rocha
