The Kinetic Theory of Gases
M. Rocha
Physics 4C
Pressure
Pressure is force per unit area
Metric unit of pressure is Pascal.
1 Pascal = 1 Newtons per square meter
A pressure < B pressure
A pressure < B pressure

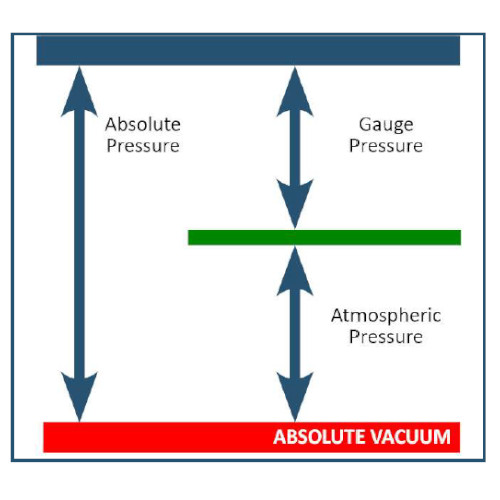
Gauge Pressure

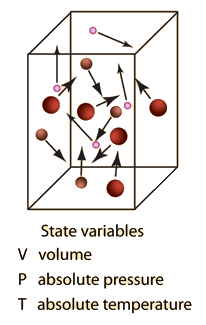
Ideal Gas Definition
An ideal gas is defined as one in which all collisions between atoms or molecules are perfectly elastic and in which there are no intermolecular attractive forces. One can visualize it as a collection of perfectly hard spheres which collide but which otherwise do not interact with each other. In such a gas, all the internal energy is in the form of kinetic energy and any change in internal energy is accompanied by a change in temperature.
Kinetic Theory of Gases

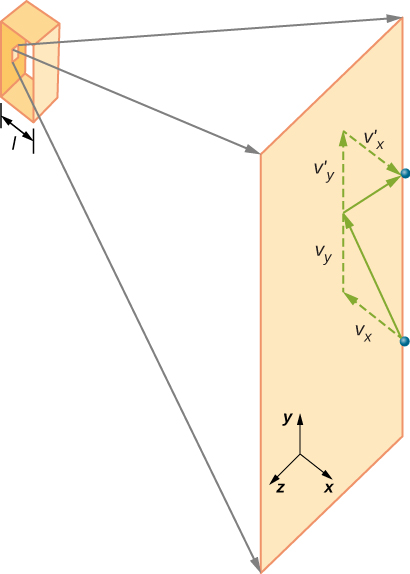
Relation Between Pressure, Volume and Average Speed of Molecules
If a molecule’s velocity changes in the x-direction, its momentum changes from −𝑚𝑣_𝑥 to +𝑚𝑣_𝑥. Thus, its change in momentum is:

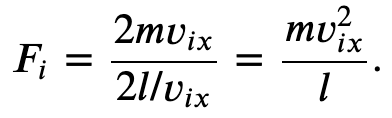
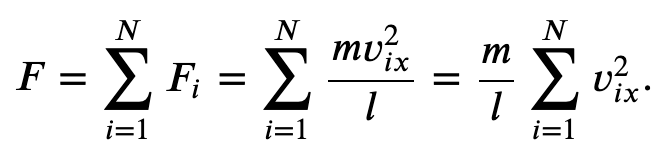
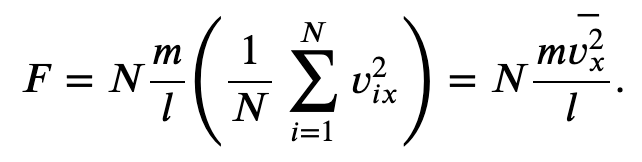
The force per molecule due to collisions on one of the walls in the x-dimension is,
And the total force due to all the molecules
Where p represents the momentum, not pressure. And we have used the fact that Δ𝑡=2𝑙/𝑣_𝑥, where l is the size of the box in one dimension.
We have used the definition of an average in the second expression.
Relation Between Pressure, Volume and Average Speed of Molecules
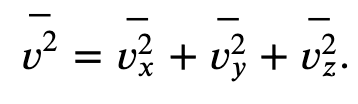
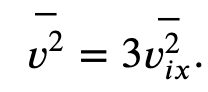
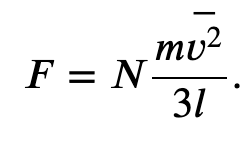
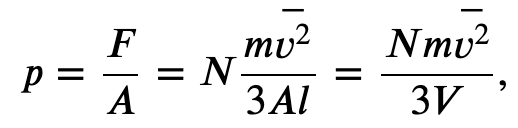
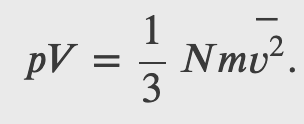
Relation Between Pressure, Volume and Average Speed of Molecules
We want the force in terms of the speed v, rather than the x-component of the velocity. Note that the total velocity squared is the sum of the squares of its components, so that
With the assumption of isotropy, the three averages on the right side are equal, so
Finally we can rewrite the force and pressure in terms of the average speed squared
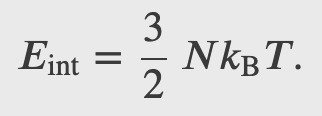
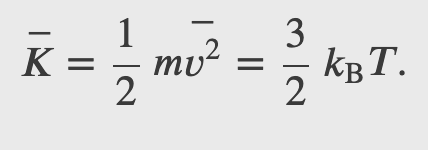
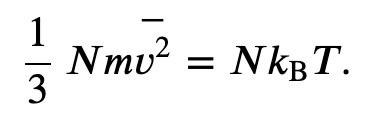
Connection to The Ideal Gas Law
From the kinetic theory we obtained the relation
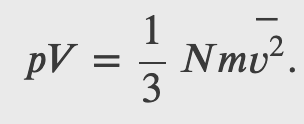
And from the ideal gas law we know
Thus
Temperature and Kinetic Energy
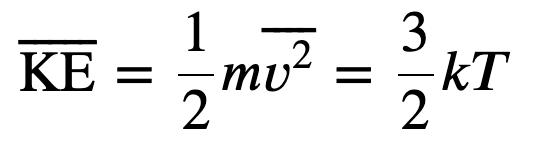
The average translational kinetic energy of molecules in an ideal gas is related to its temperature by the thermal energy equation
Where k is the boltzmann constant
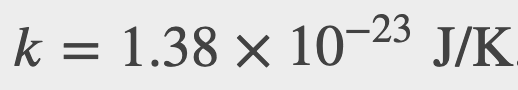
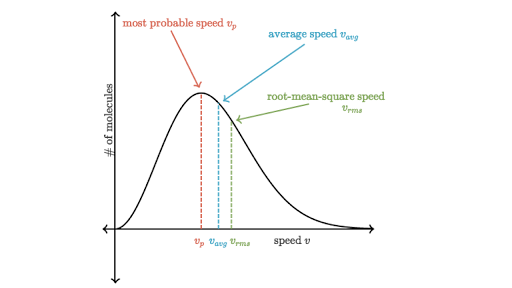

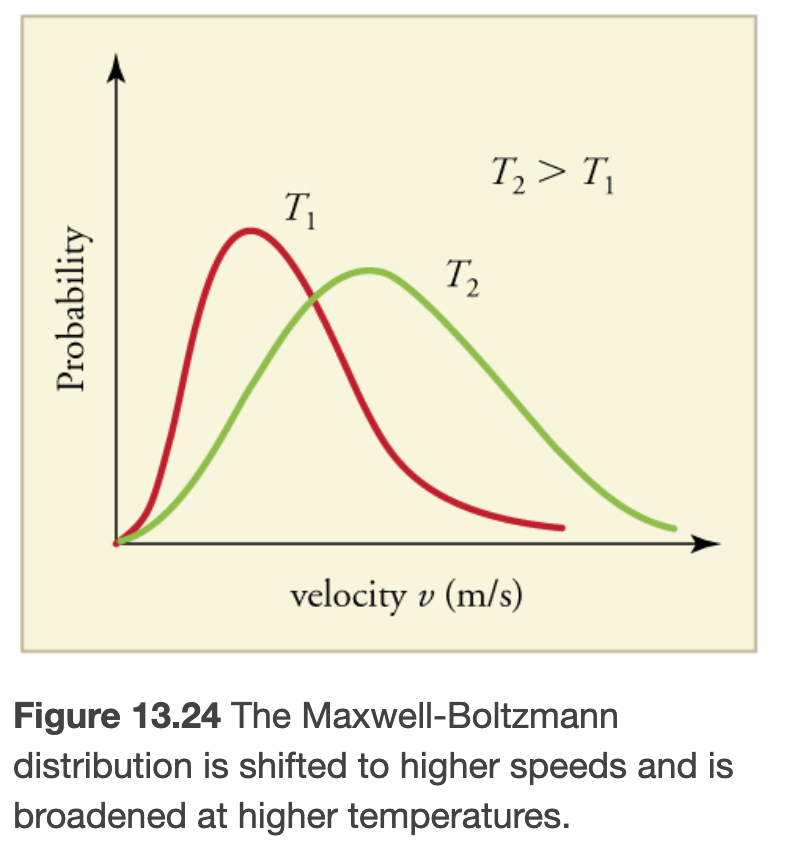
Maxwell-Boltzmann Distribution of Speeds
The distribution function for speeds of particles in an ideal gas at temperature T is
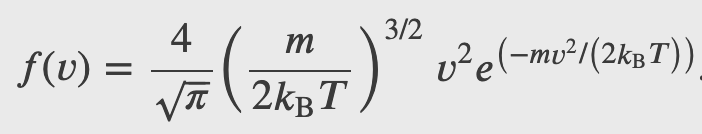

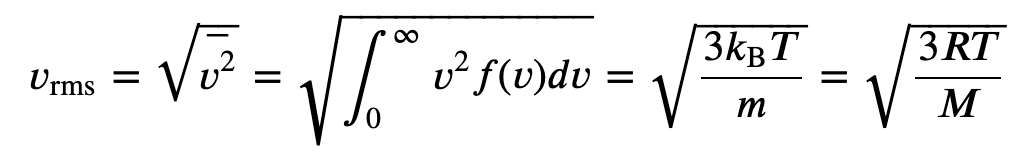
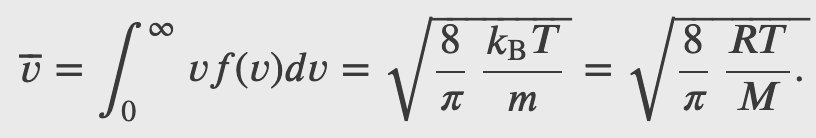
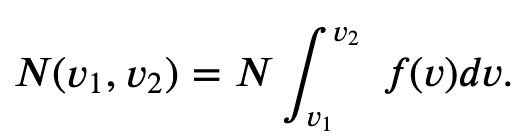
(a) What is the average kinetic energy of a gas molecule at 20.0ºC (room temperature)? (b) Find the rms speed of a nitrogen molecule (N_2) at this temperature.
Checkpoint
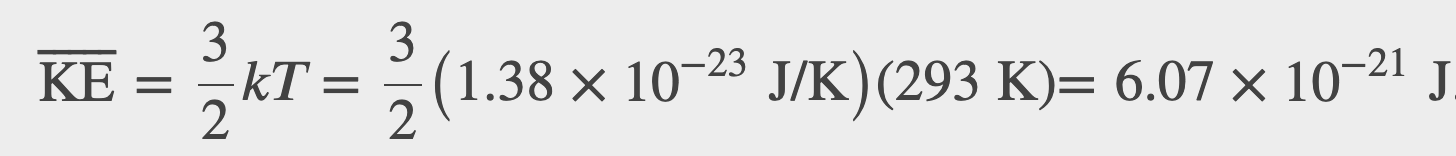

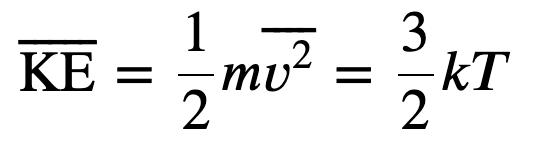
The Ideal Gas Law
Remember Boyle's Law
When the volume of a gas is decreased, the density increases and therfore pressure increases
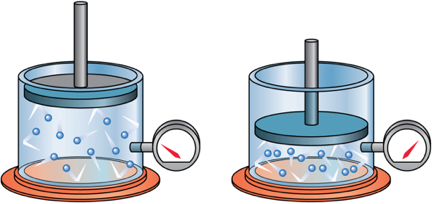

Boyle's Law is a conservation of energy equation, for cases where the internal energy is constant.
For ideal gases the internal energy is all due to temperature, i.e. the thermal energy of all molecules in the contained gas
Where N is the number of atoms/molecules in the gas, and the factor of 2/3 is introduced by relating the mechanical energy due to PV to the avg. kinetic energy of a molecules. Finally using the thermal energy equation we can get the ideal gas law
The ideal gas law, is an empirical relation between Pressure and Volume with Temperature/Thermal Energy
The Ideal Gas Law
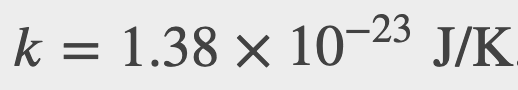
Where N is the number of atoms/molecules in the gas and k is the boltzman constant
You may also find it useful in units of moles
Where n is the number of moles in the gas and
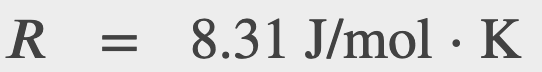
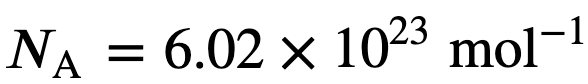
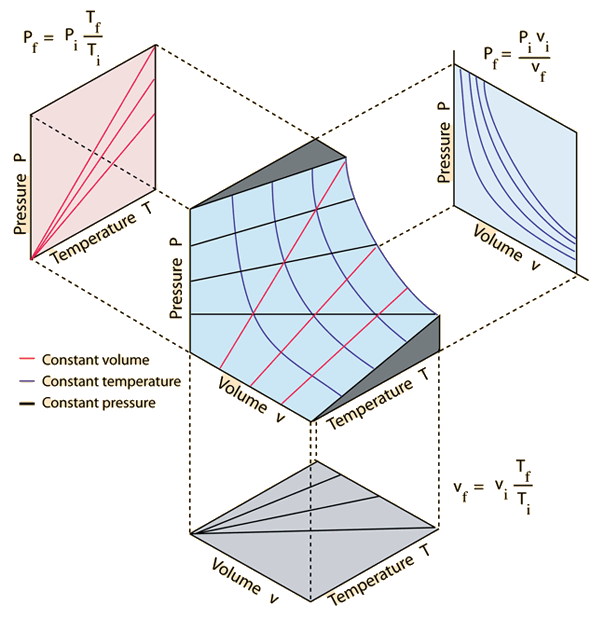
The ideal gas law, relates Pressure and Volume with Temperature
Boyle's Law
The ideal gas law describes the behavior of any real gas when its density is low enough or its temperature high enough that it is far from liquefaction (well above the boiling point). This encompasses many practical situations.
The Ideal Gas Law Applies to Most Gases Under Certain Conditions
Suppose your bicycle tire is fully inflated, with an absolute pressure of 7.00×10^5 Pa (90.0lb/in^2) at a temperature of 18.0ºC. What is the pressure after its temperature has risen to 35.0ºC ? Assume that there are no appreciable leaks or changes in volume.
Checkpoint
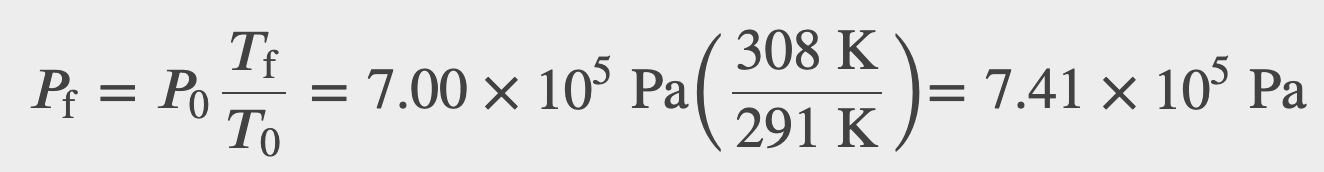
The density of air at standard conditions (𝑃 =1 atm and 𝑇=20ºC) is 1.28 kg/m^3. At what pressure is the density 0.64 kg/m^3 if the temperature and number of molecules are kept constant?
Checkpoint
Heat Capacity and Equipartition of Energy
Heat Capacity at Constant Volume
We can use the result from the kinetic theory of gases relating internal energy with temperature in order to explain the heat capacity for monoatomic ideal gases under certain conditions.
If the volume does not change, there is no overall displacement, so no work is done, and the only change in internal energy is due to the heat flow Δ𝐸_int=𝑄
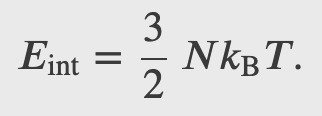
Noticed that we have replaced the mass (m) by the number of molecules (N) in the definition of heat capacity. We can also use the molar heat capacity
when using number of molecules N
when using number of moles n
Equipartition Theorem
Notice that the factor of 3 in the relation between average kinetic energy and temperature came from the isotropic assumption
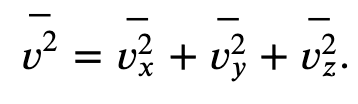
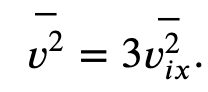
Thus, we can look at our kinetic energy of (3/2)𝑘𝑇 as the sum of contributions of (1/2)𝑘𝑇 from each of the three dimensions of translational motion.
We define a degree of freedom as an independent possible motion of a molecule, such as each of the three dimensions of translation. Then, letting d represent the number of degrees of freedom, we can write a more general heat capacity expression for constant volume
or
Equipartition Theorem
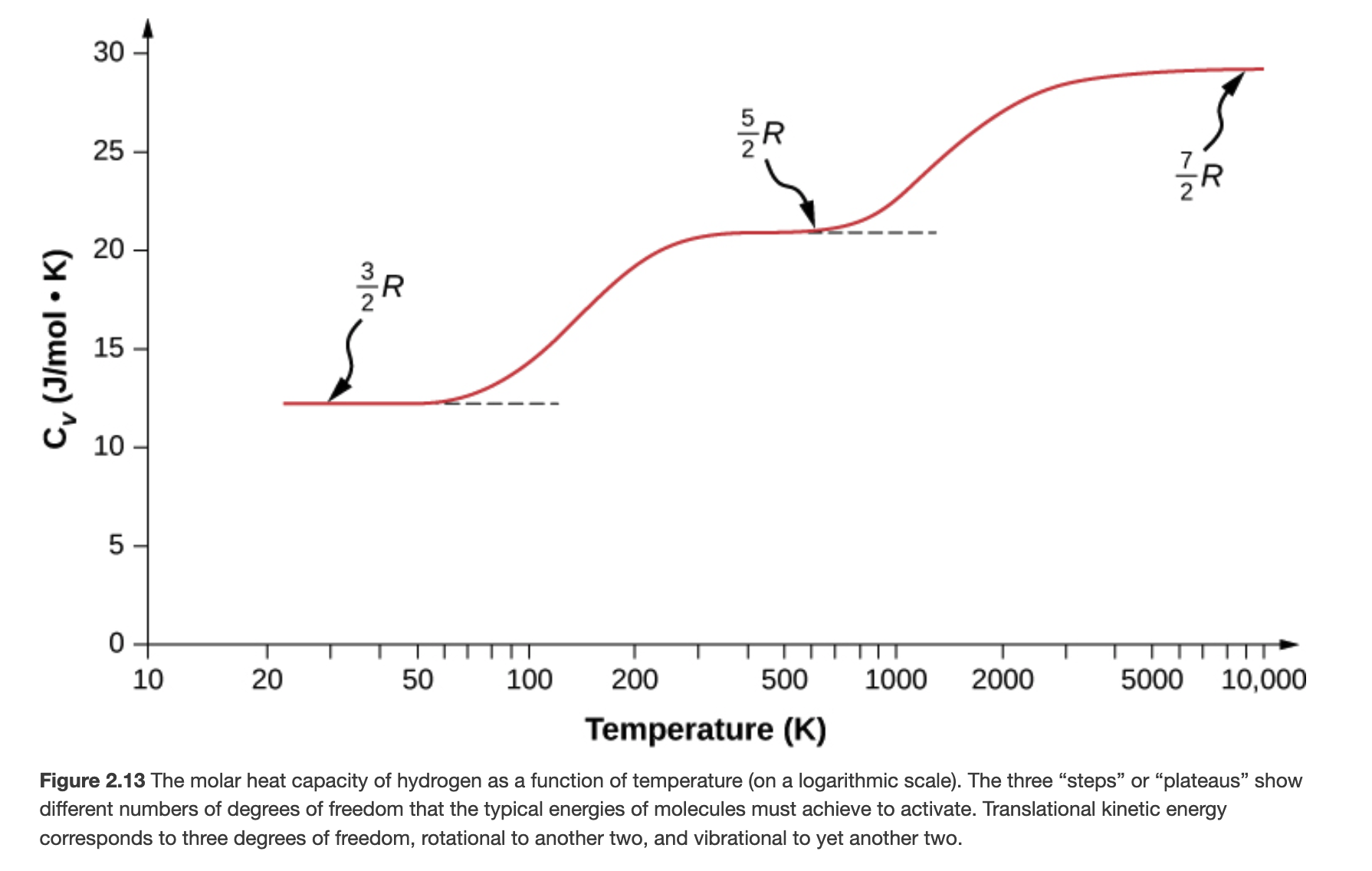
The heat capacity of a diatomic gas with 7 degrees of freedom (d=7)
The 2 degrees of freedom due to rotations only are active above a threshold temperature
The 2 degrees of freedom due to vibrations only are active above an even higher threshold temperature
Heat Capacity of Solids
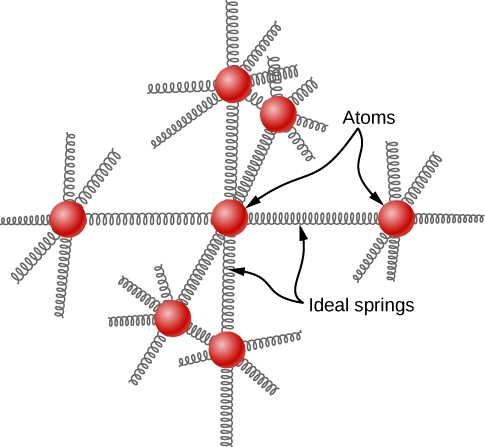
In a simple model of a solid element, each atom is attached to others by six springs, two for each possible motion: x, y, and z. Each of the three motions corresponds to two degrees of freedom, one for kinetic energy and one for potential energy. Thus 𝑑=6.
This result, known as the Law of Dulong and Petit, works fairly well experimentally at room temperature. (For every element, it fails at low temperatures for quantum-mechanical reasons. Since quantum effects are particularly important for low-mass particles, the Law of Dulong and Petit already fails at room temperature for some light elements, such as beryllium and carbon. It also fails for some heavier elements.)
Checkpoint
The atmosphere (air) is mostly composed of N_2 (78%) and O_2 (21%). What is the heat capacity at constant volume of air in units of k (or R) at room temperature (~300 K)?
HINT: At 300K rotations of the O_2 and N_2 molecules are active, but vibrations are not.
There are 5 degrees of freedom (d = 5), 3 for translational motion and 2 for rotations.
Thus C = 5/2 k, or C = 5/2 R.
C/k = C/R = 2.5
Checkpoint
A 300g piece of solid gallium (a metal used in semiconductor devices) at its melting point of only 30.0°C is in contact with 12 moles of air at 95.0°C in an insulated container. When the air reaches equilibrium with the gallium, 202g of the gallium have melted. Based on those data, what is the heat of fusion of gallium? Assume the volume of the air does not change and there are no other heat transfers.
The End
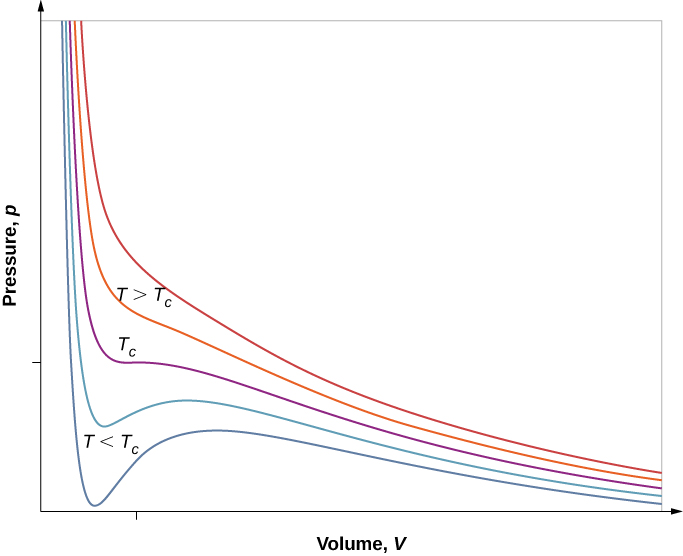
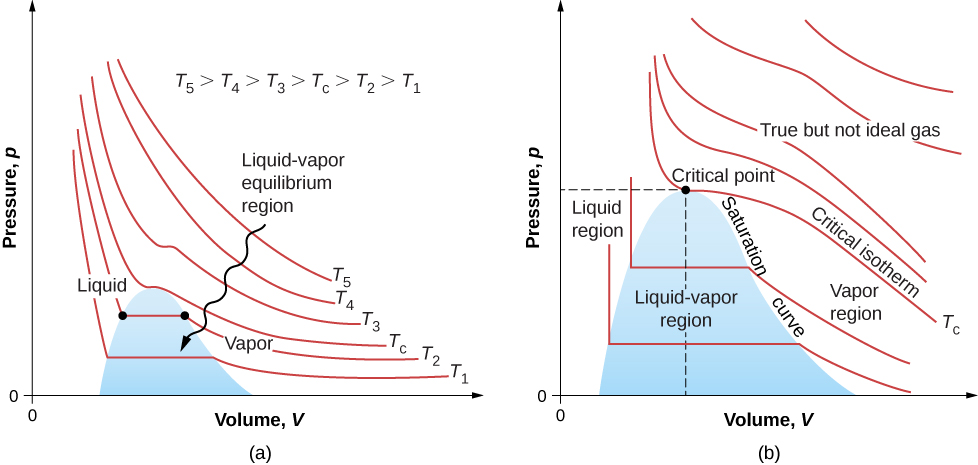
The Van der Waals Equation of State
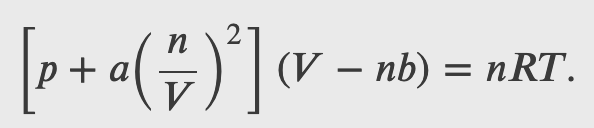
The van der Waals equation of state improves the ideal gas law by taking into account two factors. First, the attractive forces between molecules, which are stronger at higher density and reduce the pressure, are taken into account by adding to the pressure a term equal to the square of the molar density multiplied by a positive coefficient a. Second, the volume of the molecules is represented by a positive constant b, which can be thought of as the volume of a mole of molecules. This is subtracted from the total volume to give the remaining volume that the molecules can move in. The constants a and b are determined experimentally for each gas. The resulting equation is


The Kinetic Theory of Gases (Physics 4C)
By Miguel Rocha
The Kinetic Theory of Gases (Physics 4C)
- 871



