Kinematics
M. Rocha
Physics 2A - Weeks 2 & 3
Kinematics is the Study of Motion
- Displacement v.s. Distance Traveled
- Vectors v.s. Scalars
- Speed, Velocity and Acceleration
- Equations of Motion with Constant Acceleration
- Free Fall Motion
- Vectors in 2D
- Kinematics in 2D: Projectile Motion
- Satellites
In this set of slides we will cover:
Displacement
We define displacement as the change in position of an object
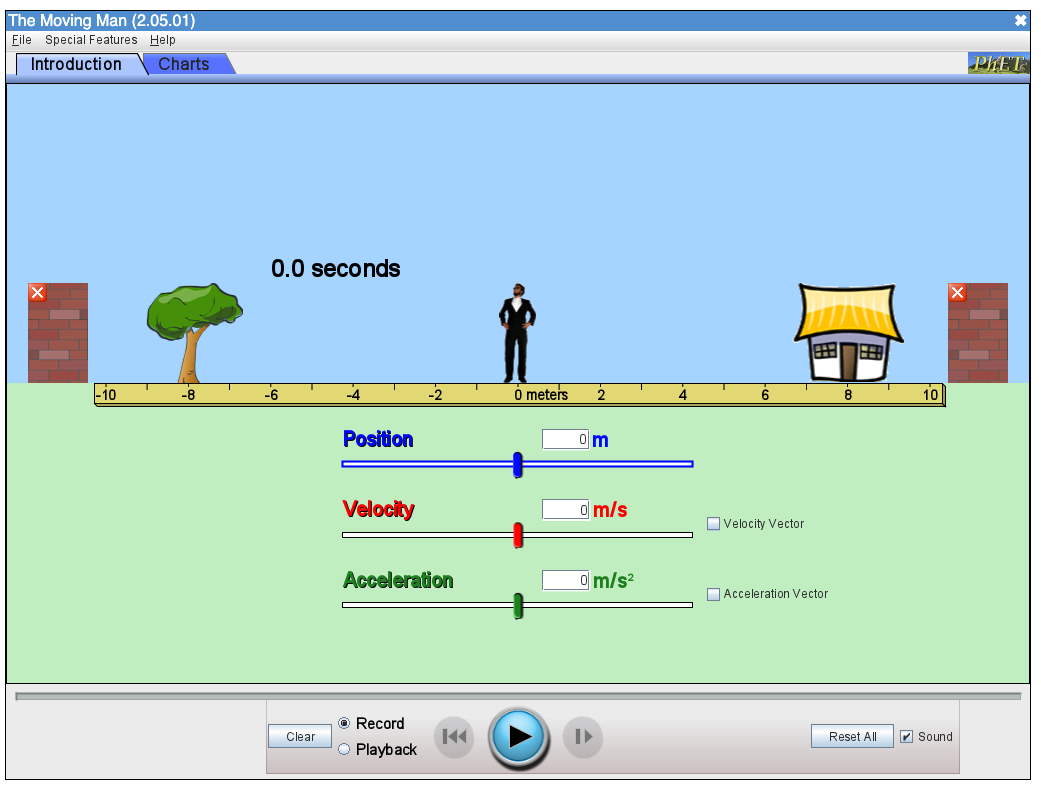
Using a cartesian coordinate system as our reference frame, we can write displacement along the x-dimension as:
\Delta x\ =\ x_{f} \ -\ x_{0}
x_{f}
\Delta x
x_{0}
where is displacement, is the final position, and is the initial position
Displacement
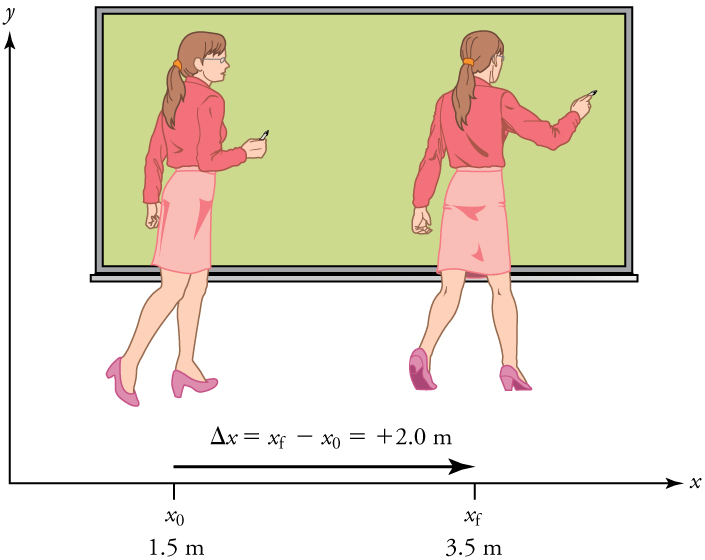
A professor paces left and right while lecturing. Her position relative to Earth is given by x . The +2.0 m displacement of the professor relative to Earth is represented by an arrow pointing to the right.
Displacement
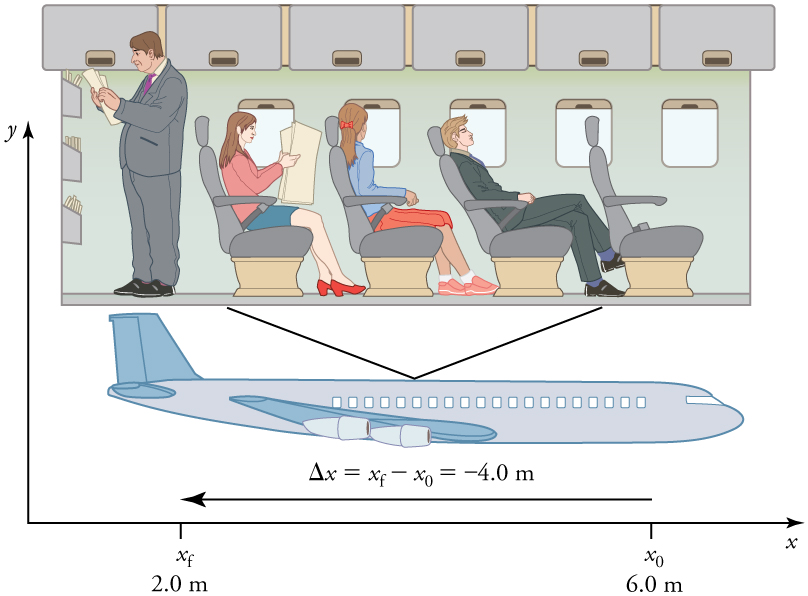
A passenger moves from his seat to the back of the plane. His location relative to the airplane is given by x . The −4.0 m displacement of the passenger relative to the plane is represented by an arrow toward the rear of the plane. Notice that the arrow representing his displacement is twice as long as the arrow representing the displacement of the professor (he moves twice as far)
Displacement v.s. Distance
Distance is the magnitude of the displacement, ignoring the direction. Thus distance has no sign.
If the displacement of the passenger in the previous slide is -4 m, the distance is |-4 m| = 4 m, where || means magnitude or absolute value
NOTE: Total distance traveled is the net distance traveled accounting for any back and forth motion, e.g. if the passenger in the previous slide move back and forth several times before ending in his final position, the total distance traveled would be greater than its distance.
Vectors v.s. Scalars
Vectors - magnitude and direction
Scalars - only magnitude
Examples:
Displacement
Velocity
Acceleration
Force
Examples:
Distance
Speed
Mass
Volume
Speed, Velocity and Acceleration
Velocity vs. Speed
Velocity is a Vector - magnitude and direction
Speed is a Scalar - magnitude
\mathrm{Speed} = \frac{\mathrm{distance}}{\mathrm{time}}
\mathrm{Velocity} = \frac{\mathrm{displacement}}{\mathrm{time}}
In a specific direction
Instantaneous vs. Average
\overline{v} = \frac{\Delta x}{\Delta t} = \frac{x_\mathrm{f}-x_\mathrm{0}}{t_\mathrm{f}-t_\mathrm{0}}
\mathrm{Instantaneous \ Velocity} = \lim_{\Delta t \to 0}\frac{\Delta x}{\Delta t}
Average velocity is the velocity calculated from the displacement over an interval of time
Instantaneous velocity is when you measure speed over an infinitesimally small interval of time
\overline{v} = \frac{\Delta x}{\Delta t} = \frac{x_\mathrm{f}-x_\mathrm{0}}{t}
, If
t_\mathrm{0} = 0
\Rightarrow
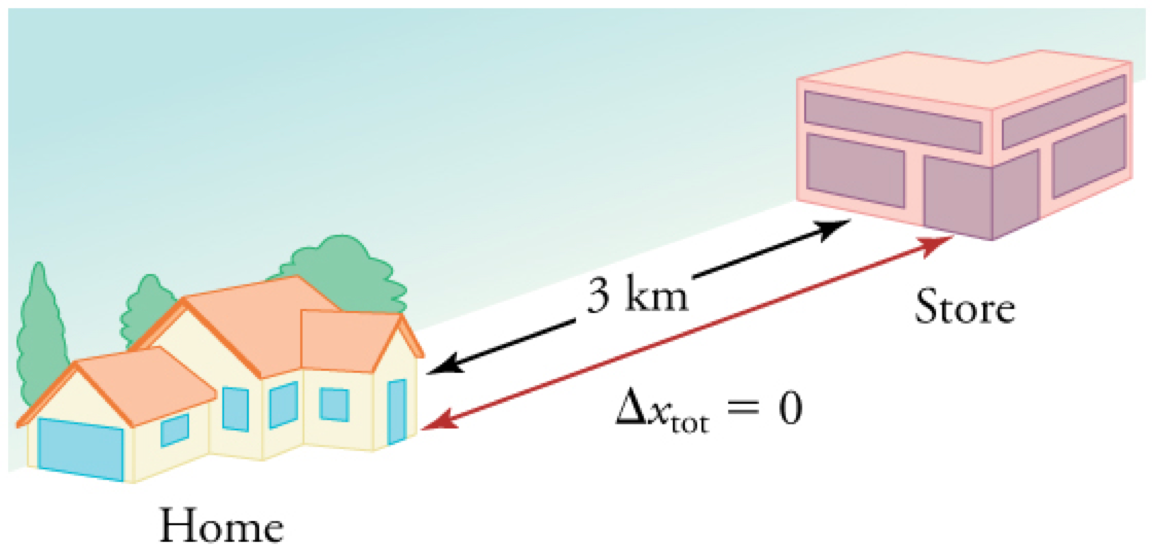
During a 30-minute round trip to the store, the total distance traveled is 6 km. The average speed is 12 km/h. The displacement for the round trip is zero, since there was no net change in position. Thus the average velocity is zero.
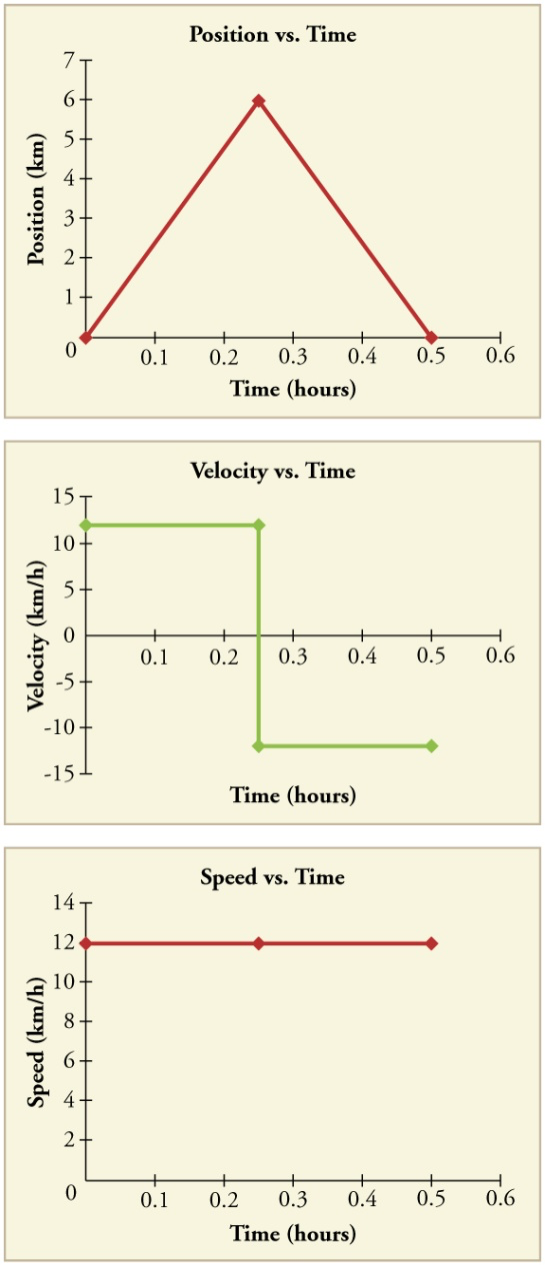
Average Speed vs. Average Velocity
Checkpoint
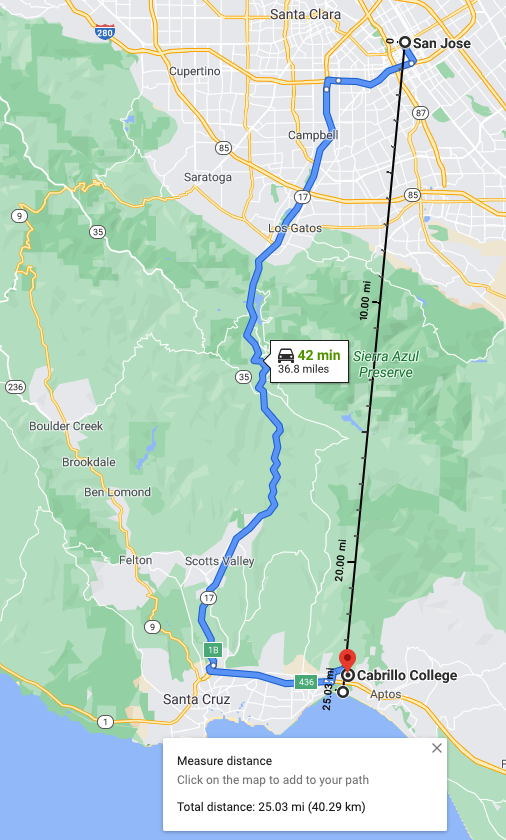
What was your average speed if you commuted from San Jose to Cabrillo (36 miles) in 36 min
\mathrm{Average \ Speed} = \frac{36 \ \mathrm{miles}}{36 \ \mathrm{minutes}}
= 1 \frac{\mathrm{miles}}{\mathrm{min}}[\frac{60 \ \mathrm{min}}{\mathrm{hour}}] = 60 \frac{\mathrm{miles}}{\mathrm{hour}}
What about your average velocity?
\overline{v} = \frac{25 \ \mathrm{miles}}{36 \ \mathrm{min}} \approx 42 \frac{\mathrm{miles}}{\mathrm{hour}}\ \mathrm{SSW}
Average Acceleration
\overline{a} = \frac{\mathrm{Change \ of \ velocity}}{\mathrm{Time \ interval}} = \frac{\Delta \ v}{\Delta \ t} = \frac{v_\mathrm{f}-v_\mathrm{0}}{t_\mathrm{f}-t_\mathrm{0}}
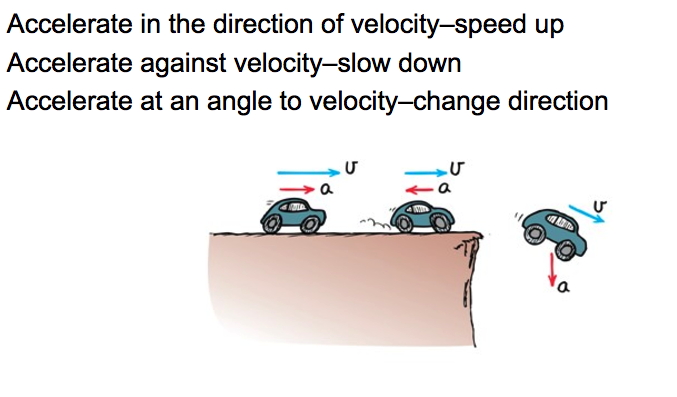
Acceleration is a vector!
Acceleration is a vector!
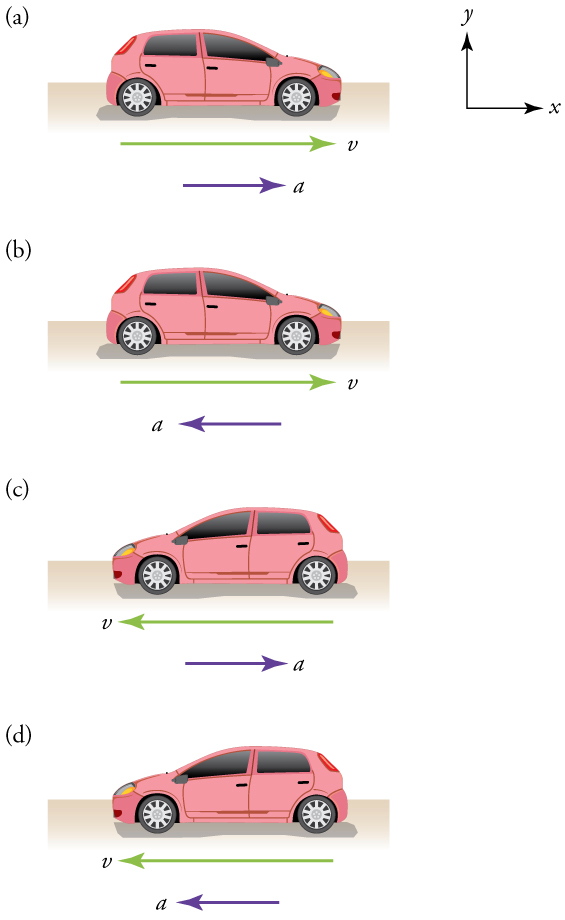
Chekpoint
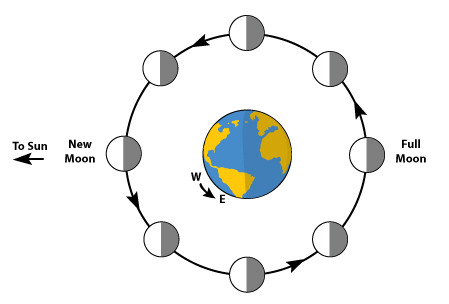
If the Moon travels around the Earth at a constant speed of 1 km/s, is it accelerating?
Yes! The direction of is motion is changing
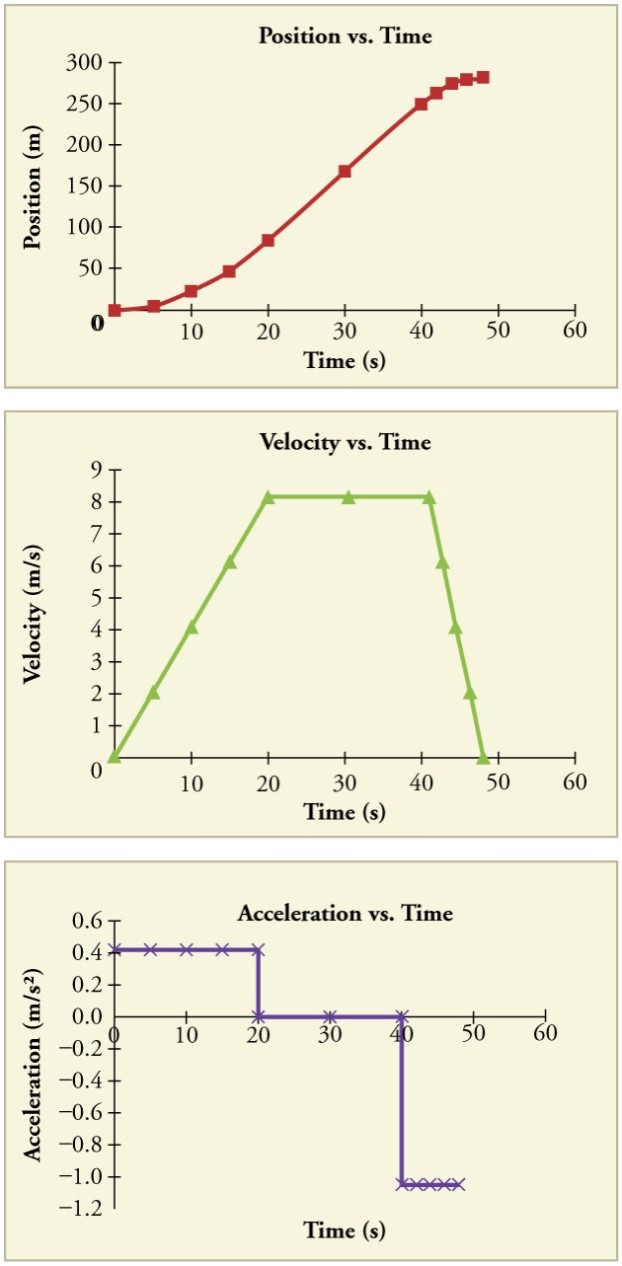
Graphing Motion
Checkpoint
If a car goes from rest to 36 km/h in 10s, what is its acceleration?
\mathrm{Acceleration} = \frac{\Delta \ v}{\Delta \ t} = \frac{ 36 \ \mathrm{km/h}}{10 \ \mathrm{s}} = 3.6 \frac{ \mathrm{km}}{\mathrm{h \cdot s}}[\frac{1 \ \mathrm{h}}{3600 \ \mathrm{s}}]
= 1\times 10^{-3} \frac{ \mathrm{km}}{\mathrm{s}^2}
\mathrm{Acceleration} = \frac{\mathrm{Chance \ of \ velocity}}{\mathrm{Time \ interval}} = \frac{\Delta \ v}{\Delta \ t}
Motion Under Constant Acceleration
Notation
t_\mathrm{0} = 0
\overline{a} = a = \frac{\Delta \ v}{\Delta \ t}
\Rightarrow \Delta \ v = \mathrm{a} \ \Delta \ t
\Rightarrow (v \ - \ v_0) = a \ t
\Rightarrow v = a \ t + v_0
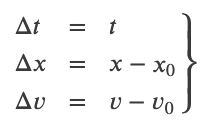
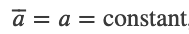
Velocity aquired
Equations of motion: Velocity acquired
( constant a )
\overline{v} \ = \frac{\Delta \ x}{\Delta \ t}
\Rightarrow \Delta \ x = \overline{v} \ \Delta \ t
\Rightarrow (x \ - \ x_0) = \frac{(v \ + \ v_0)}{2} \ t
\Rightarrow x = \frac{a}{2} \ t^2 + v_0 \ t + x_0
Final Position
\Rightarrow (x \ - \ x_0) = \frac{a t + 2v_0}{2} \ t
Equations of motion: Final Position
Eq. 2, average v under constant a
\overline{v} \ = \frac{(v \ + \ v_0)}{2}
Eq. 1
From Eq. 1
Using Eq. 2
Using Vel. Aquired Eq.
Free Fall
Free fall (ignoring air resistance) is a great example of motion under constant acceleration
a_y = -g = -9.8 \ \frac{m}{s^2} \simeq -10 \ \frac{m}{s^2}
Free Fall
\Rightarrow v_y = a_y \ t
From rest ( )
v_0 = 0
y = \frac{a_y}{2} \ t^2
Set
t_0 = y_0 = 0
a_y = -g = -9.8 \ \frac{m}{s^2} \simeq -10 \ \frac{m}{s^2}
v = a \ t
d = \frac{a}{2} \ t^2
Checkpoint 4
,
| t (s) | V (m/s) | d (m) |
|---|---|---|
| 0 | ||
| 2 | ||
| 4 | ||
| 6 | ||
| 8 | ||
| 10 |
| 0 | 0 |
|---|---|
| 20 | 20 |
| 40 | 80 |
| 60 | 180 |
| 80 | 320 |
| 100 | 500 |
a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}
d = \frac{a}{2}t^2 \Rightarrow d \propto t^2
Constant Acceleration
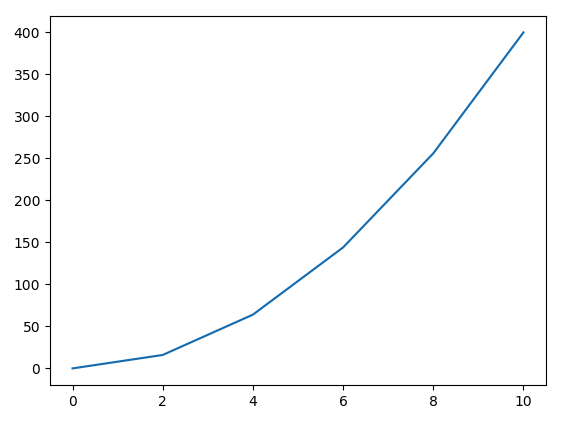
velocity
distance
Time
Time
v = a \ t \Rightarrow v \propto t
Constant Acceleration
velocity (m/s)
Time (s)
v = a \ t \Rightarrow v \propto t
If acceleration is the slope of the velocity vs. time plot how do you find the acceleration given the plot?
a = \mathrm{slope}
a = \mathrm{slope} = \frac{\mathrm{rise}}{\mathrm{run}} = \frac{100\frac{m}{s}}{10 s} = 10\frac{m}{s^2}
Non-Constant Acceleration
Physics of skydiving
F_{\mathrm{air \ Resistance}} = R
F_{\mathrm{gravity}} = mg
a = \frac{F_\mathrm{net}}{m} = \frac{mg - R}{m} = g-\frac{R}{m}
Is acceleration constant?
R \propto v \Rightarrow a \propto v
What is a when R = 0?
What is a when R/m = g?
What is a when R/m > g ?
No,
a = g, \ \mathrm{freefall}
a = 0, \ \mathrm{terminal \ velocity}
a < 0, \ \mathrm{decelration}
Vectors In 2D
Adding Vectors
The sum of two or more vectors is called the resultant.
To find the resultant of two vectors that don't act in exactly the same or opposite direction , we use the pralelogram rule
-3 N +
2 N
-1 N
=>
2 N
3 N
R = \sqrt{X^2 + Y^2} = \sqrt{3^2 + 2^2} = \sqrt{13}
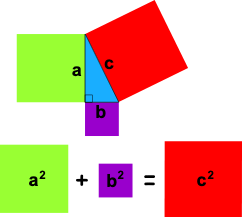
Pythagorean theorem
2 N
3 N
=
Pythagorean Theorem
Velocity is a Vector - magnitude and direction
Cross Wind
What is the magnitude of the resultant when adding the two vectors on the screen?
4000 N
- 4000 N
R = \sqrt{X^2 + Y^2} = \sqrt{(-4000)^2 + 4000^2} = \sqrt{4000^2 (-1^2 + 1^2)} = 4000\sqrt{2} \ N
Checkpoint
Adding Non-Orthogonal Vectors
If not orthogonal (perpendicular to each other), the parallelogram rule still works but you can not use the Pythagorean theorem to compute the magnitude of the resultant
2 N
3 N
If not orthogonal (perpendicular to each other), you can always decompose the given vectors into orthogonal vectors (x and y components) that you can simply add
2 N
3 N
Adding Non-Orthogonal Vectors
If not orthogonal (perpendicular to each other), you can always decompose the given vectors into orthogonal vectors (x and y components) that you can simply add
2 N
3 N
Adding Non-Orthogonal Vectors
If not orthogonal (perpendicular to each other), you can always decompose the given vectors into orthogonal vectors (x and y components) that you can simply add
2 N
3 N
2 N
3 N
=
Adding Non-Orthogonal Vectors
Vector decomposition
\sin{\theta} = \frac{A_y}{A}
\cos{\theta} = \frac{A_x}{A}
\tan{\theta} = \frac{A_y}{A_x}
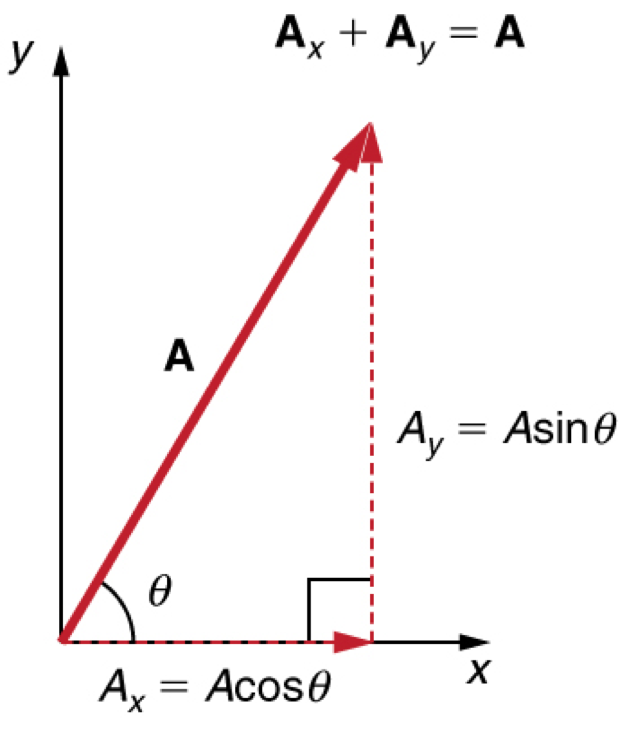
Trigonometry Review
\theta =
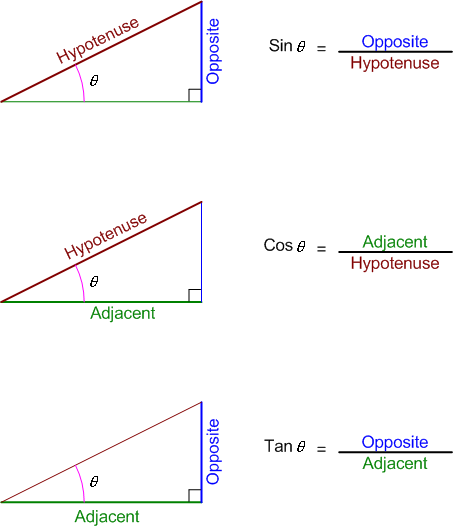
theta is the angle opposite to the right angle
\sin{\theta} = \frac{A_y}{A}
\cos{\theta} = \frac{A_x}{A}
\tan{\theta} = \frac{A_y}{A_x}
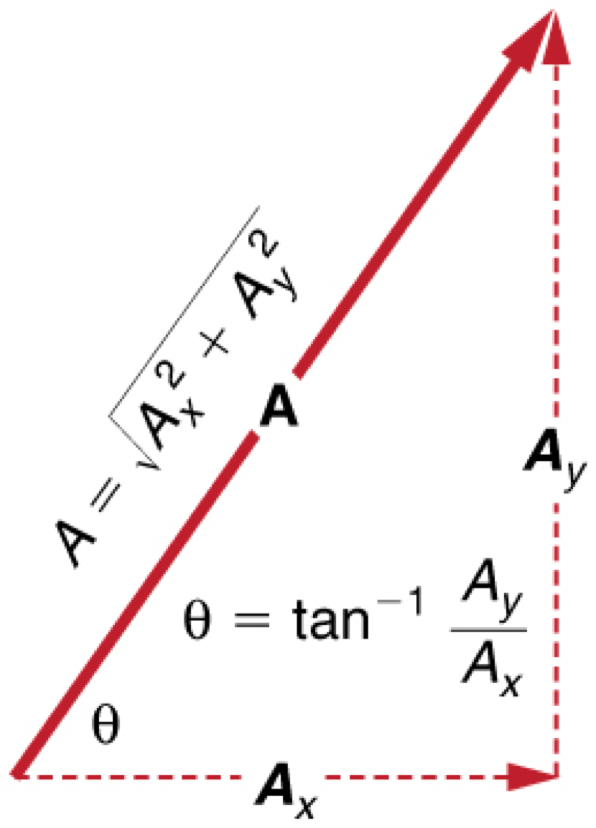
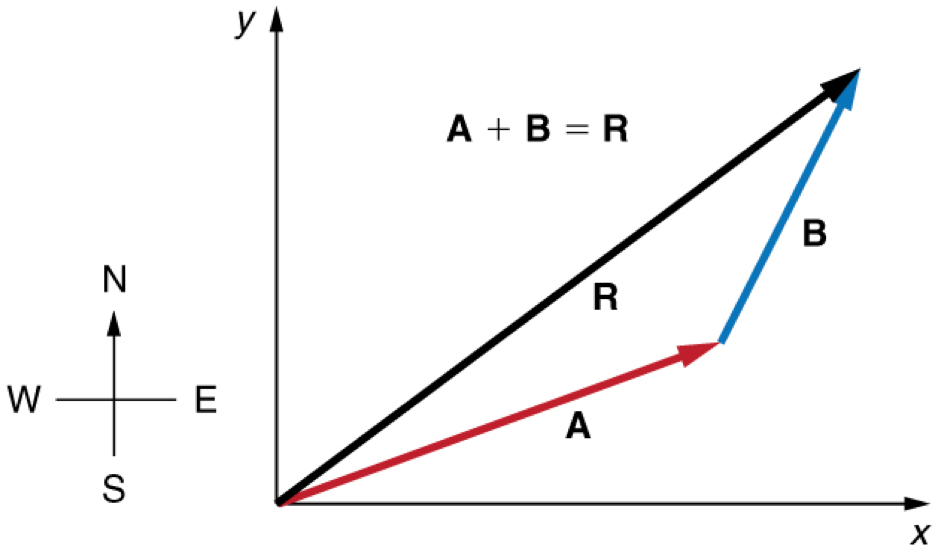
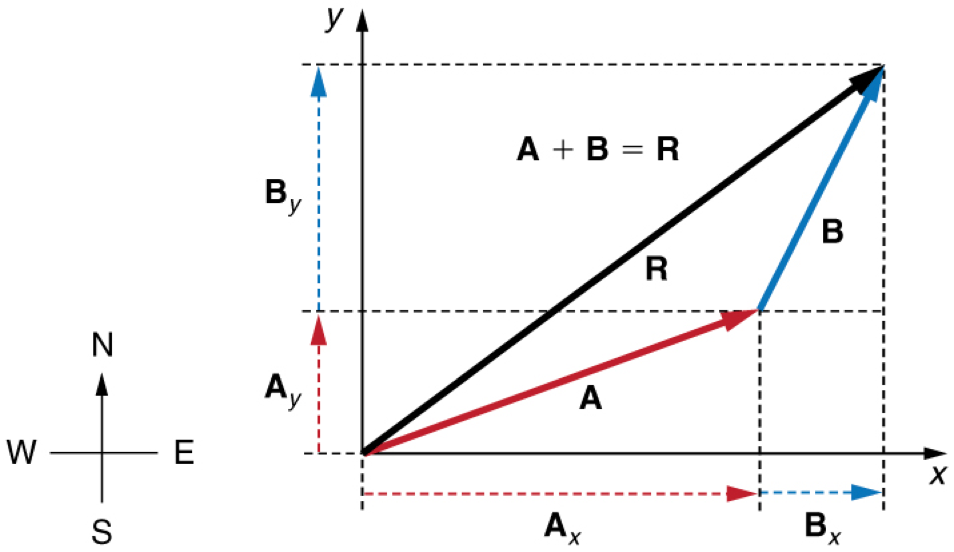
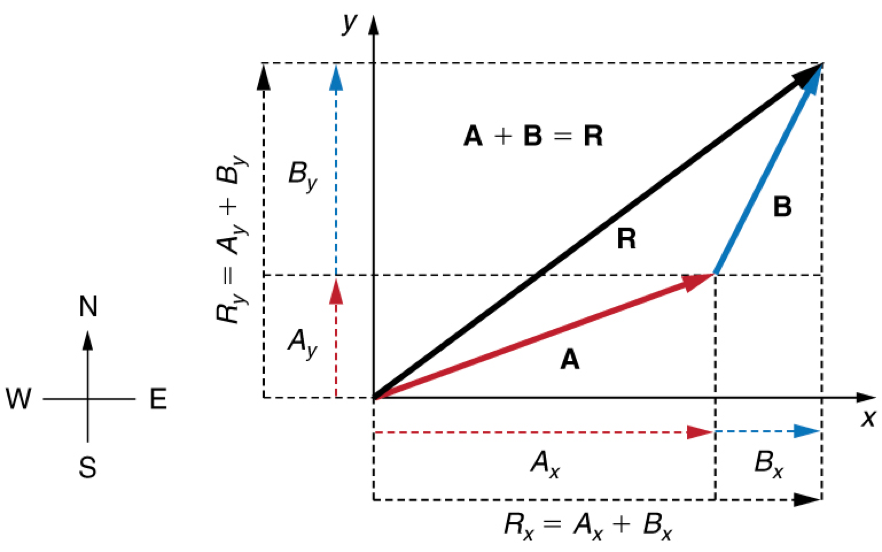
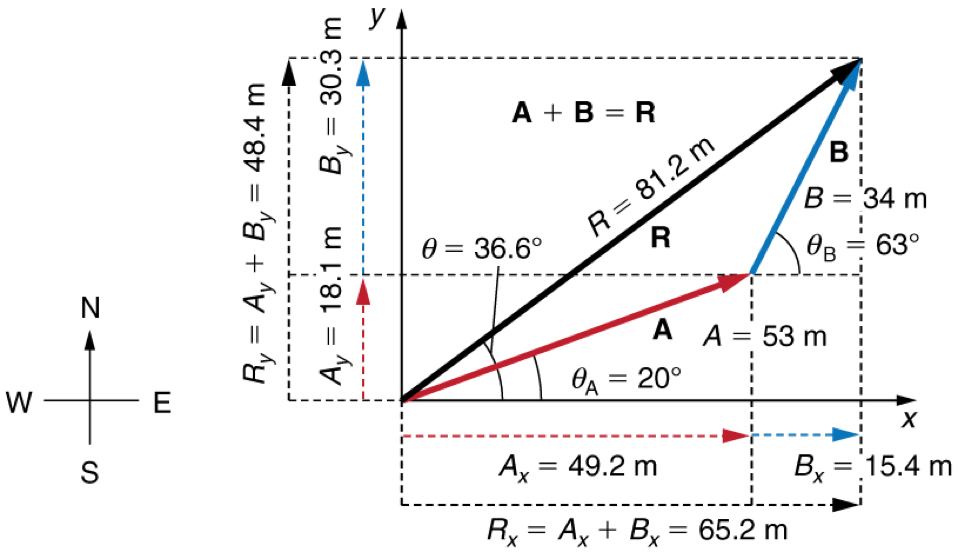
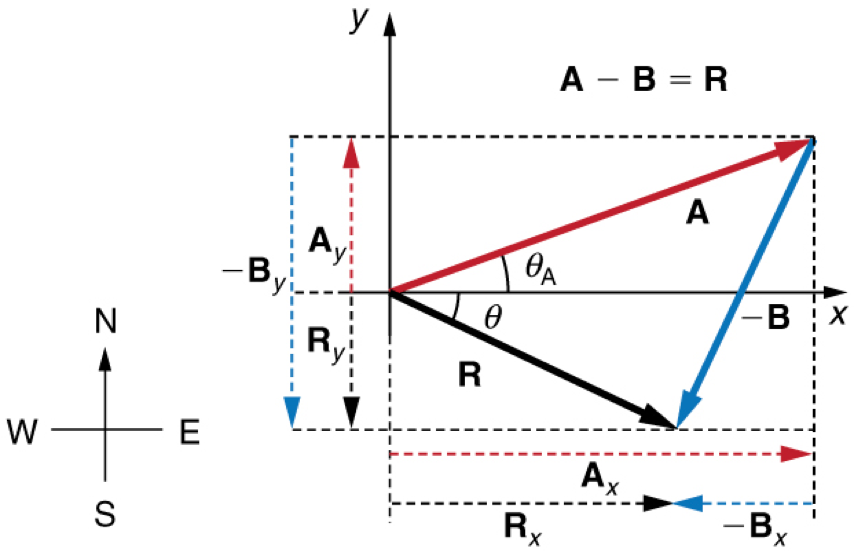
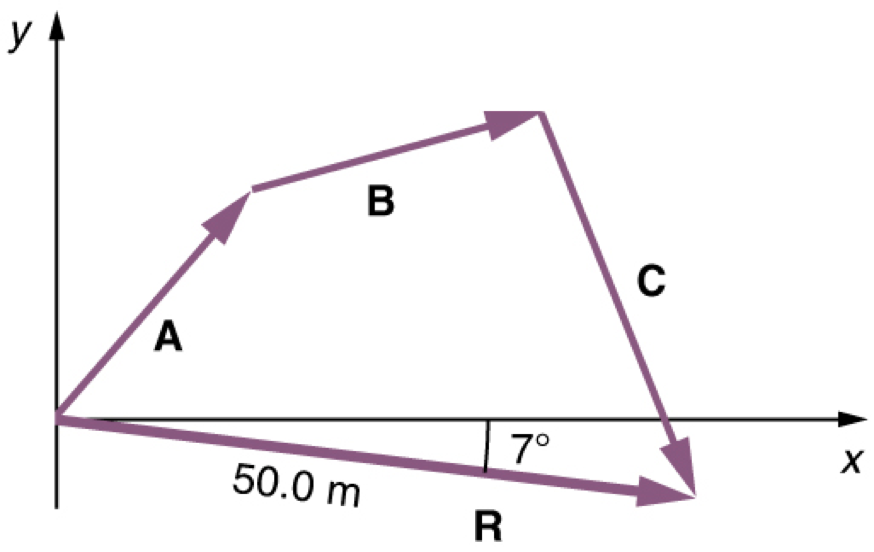
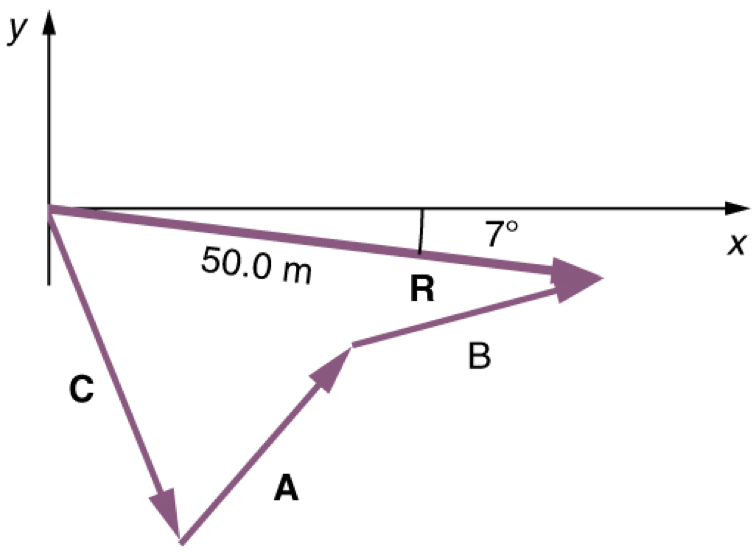
Adding More Than Two Vectors
Kinematics In 2D
Projectile Motion
\Rightarrow v_y = a_y \ t
From rest ( )
v_0 = 0
y = \frac{a}{2} \ t^2
Set
t_0 = y_0 = 0
a_y = -g = -9.8 \ \frac{m}{s^2} \simeq -10 \ \frac{m}{s^2}
Remember Free Fall Motion?
Checkpoint
How far down (distance) would you fall in 1 second after you base jump from a cliff. Ignore air resistance.
d = 5 meters after 1 second
d = \frac{a}{2} \ t^2
a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}
,
Remember Free Fall Motion?
v_y = a_y \ t
y= \frac{a}{2} \ t^2
,
y = -5 meters after 1 second
5m in 1s
a_y = -g = -9.8 \ \frac{m}{s^2} \simeq -10 \ \frac{m}{s^2}
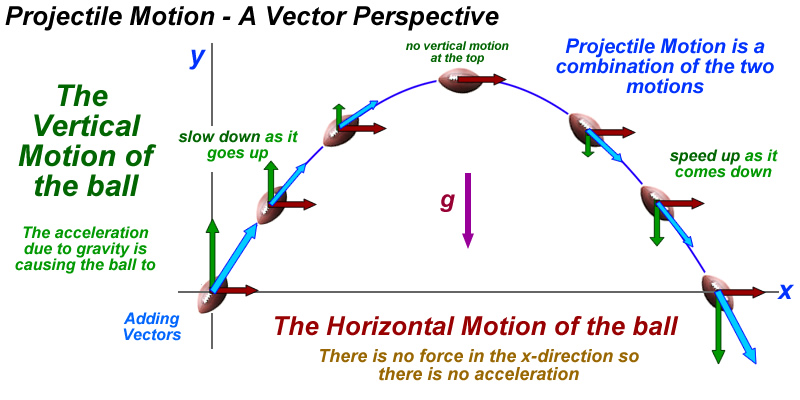
Projectile Motion is just Free Fall Motion with an horizontal velocity component
Free Fall:
V_y = a_yt + v_{y_i}
V_x = 0
Projectile:
V_y = a_yt + v_{y_i}
V_x = v_{x_i} (\mathrm{constant})
V_y
V_x
V_y
The key to understand Projectile Motion is to treat Vx and Vy separately
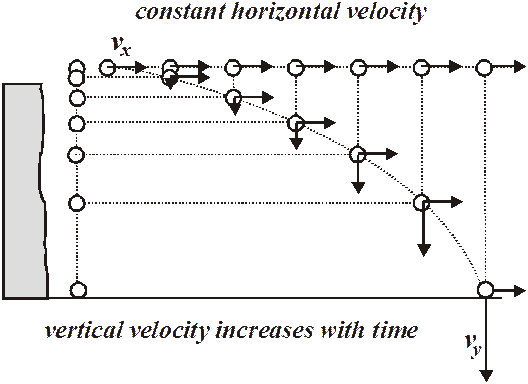
Vx and Vy are independent from each other
The key in understanding Projectile Motion is to treat Vx and Vy separately
Checkpoint
If I kick a soccer ball (from the ground), and it reaches a height of 20 meters, for how long would it be on the air before it hits the ground (HINT: The distance and time going up should be the same as when going down )?
d = \frac{a}{2} \ t^2
a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}
,
t_{up} = t_{down} = \sqrt{\frac{2d}{a}} = \sqrt{\frac{ 2 \ (20 \ m)}{10 \ m/s^2}} = \sqrt{4 \ s^2} = 2 \ s
Total time = tup + tdown = 4 seconds
Checkpoint
If I kick a soccer ball (from the ground) with a horizontal velocity of 20 m/s, and it reaches a hight of 20 meters, how far would it travel in the horizontal direction (i.e. how far would it land )?
d = \frac{a}{2} \ t^2
a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}
,
t_{up} = t_{down} = \sqrt{\frac{2d}{a}} = \sqrt{\frac{ 2 \ (20 \ m)}{10 \ m/s^2}} = \sqrt{4 \ s^2} = 2 \ s
Total time = tup + tdown = 4 seconds
Horizontal Distance = 20 m/s ( 4 seconds) = 80 m
v_\mathrm{horizontal} = \frac{d_\mathrm{horizontal}}{t}
d_\mathrm{horizontal} = v_\mathrm{horizontal}\ t = 20 \frac{m}{s} \ (4 \ s) = 80 \ m
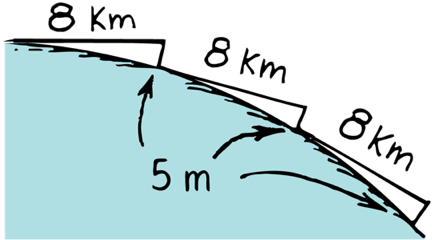
If a projectile falls 5m in 1s,
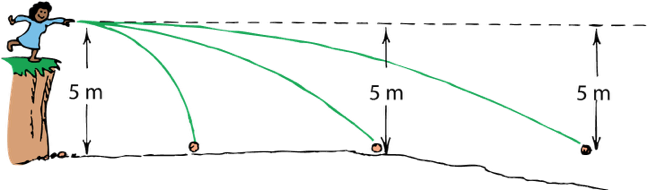
and the curvature of earth is so that it drops 5m for every 8 km
What happen if you throw a rock with an horizontal velocity of 8000 m/s = km/s (18,000 mi/h)?
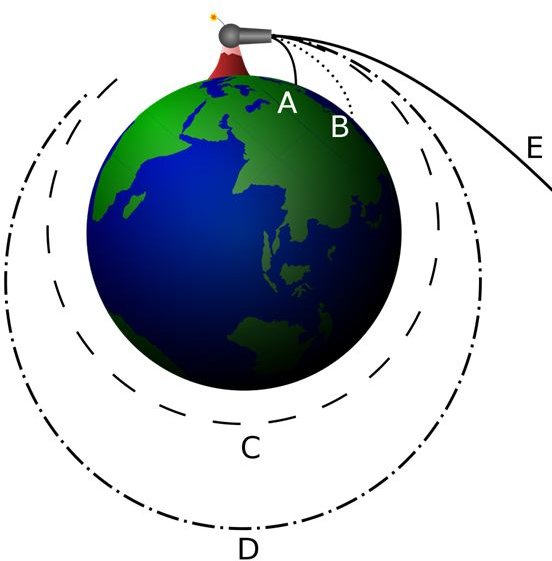
Satellites
Satellites
Satellites
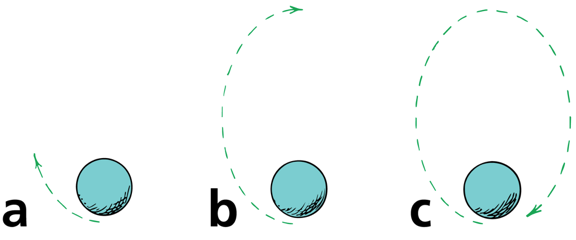
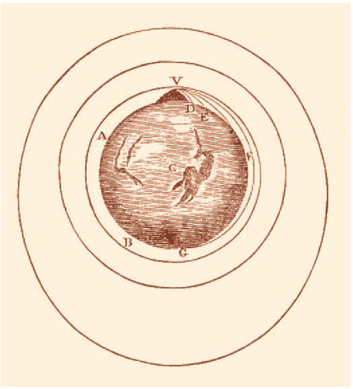
A satellite moves in an elliptical orbit
a) When the satellite exceeds 8 km/s, it overshoots a circle. b) At its maximum separation, it starts to come back toward Earth.
c) The cycle repeats itself.
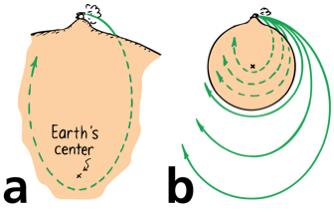
Satellites
a) A projectile's path is a section of an elliptical orbit
b) a satellite moves in an elliptical orbit
Scape Velocity
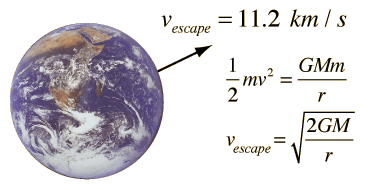
Neglecting air resistance if you throw a rock with a velocity greater than 11.2 Km/s (25000 miles/h), it wont come back
The End
Kinematics (Physics 2A)
By Miguel Rocha
Kinematics (Physics 2A)
Physics 11
