Momentum and Energy
M. Rocha
Physics 2A

Elephant has more inertia than skaterat

m < M

Moving
Not Moving
Elephant has no momentum at rest
What about momentum?

Moving
Moving
Elephant got momentum!


Momentum is inertia in motion
A container ship has lots of momentum even when moving slow because it has a lot of mass

Checkpoint
Which has more momentum, a 3000 kg elephant moving at 1 km/h or a 0.3 kg mice moving at 10000 km/h?
Both have the same momentum of 3000 kg km/h
If the mass is constant (most cases), the change of momentum over time is equal to force by Newton's 2nd law
Momentum and Force
Momentum is a vector pointing in the direction of the velocity
Impulse is change in momentum
Impulse-momentum relationship
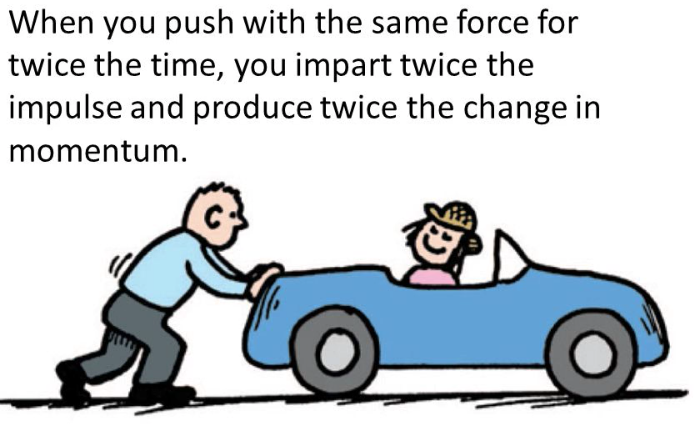
Impulse-Momentum Relationship
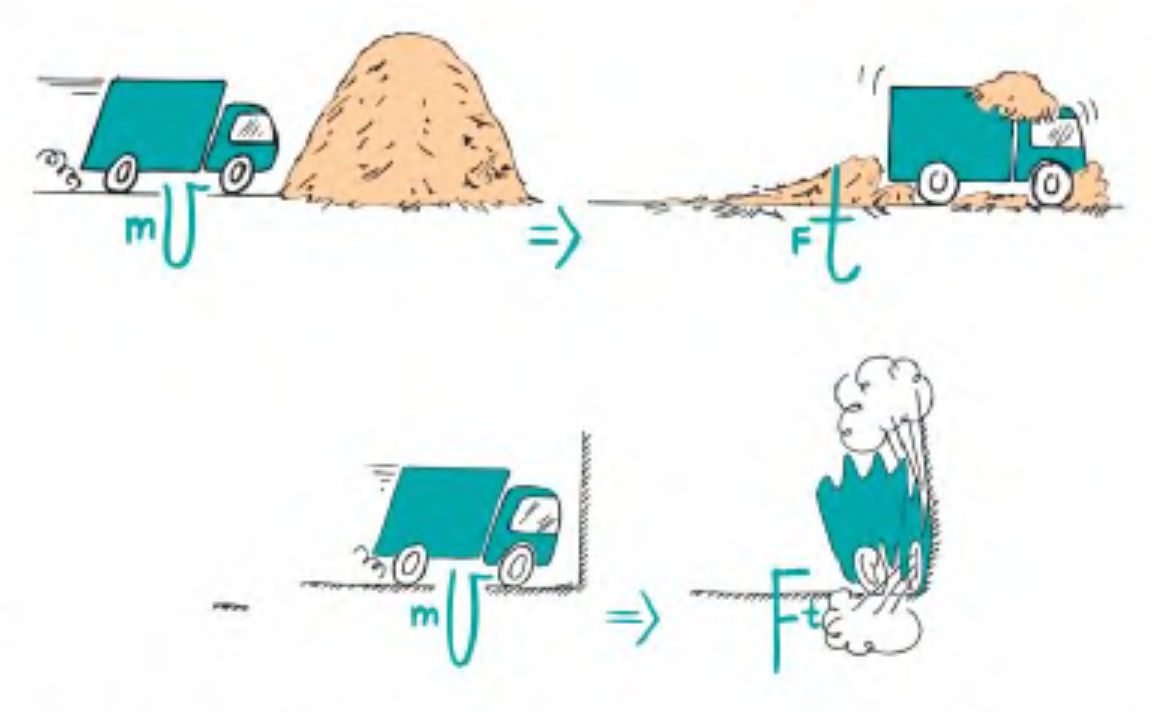
Large t, small F
Large F, small t
Impulse-Momentum Relationship

Dynamic ropes reduce the force by increasing the time to stop
Checkpoint
If a dynamic rope is able to increase the duration of a rock climber's fall by four times, how much would the force of impact change?
The force is reduced by four
Bouncing increases impulse
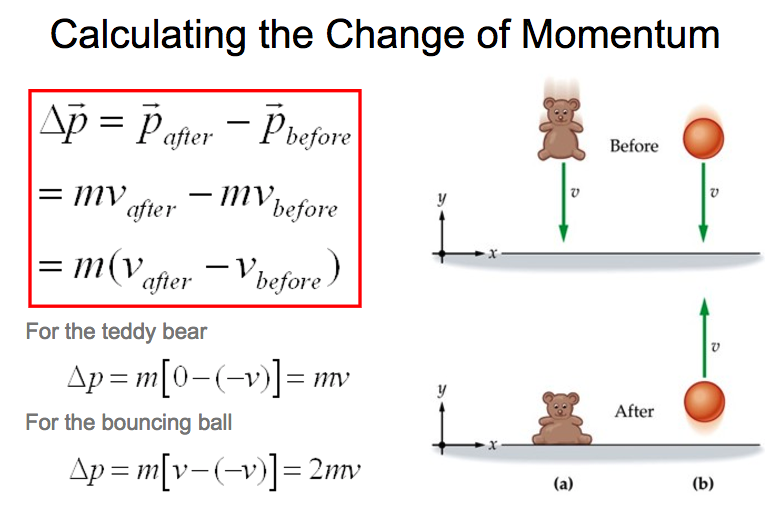
Change in momentum of teddy bear vs. bouncing ball
Bouncing increases impulse
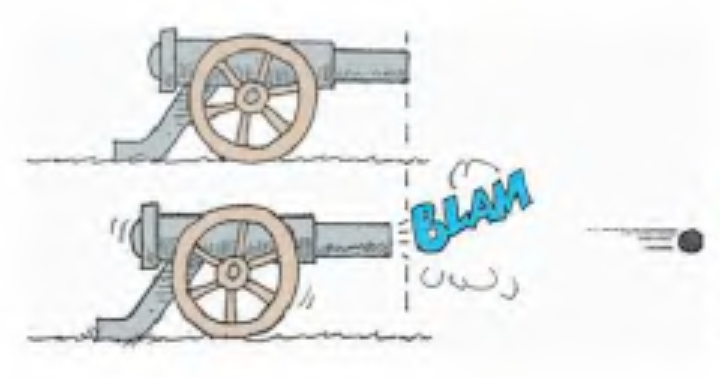
Conservation of momentum
In the absence of an external force, the momentum of a system remains unchanged
Initial momentum
Final momentum
Conservation of momentum

Initial momentum
Final momentum
Big Fish
Small Fish
Small Fish
Big Fish
?
Elastic Collisions
Inelastic Collisions
Energy and momentum are conserved
Momentum is conserved but energy is not
Momentum is always conserved regardless of the type of collision!
vs.
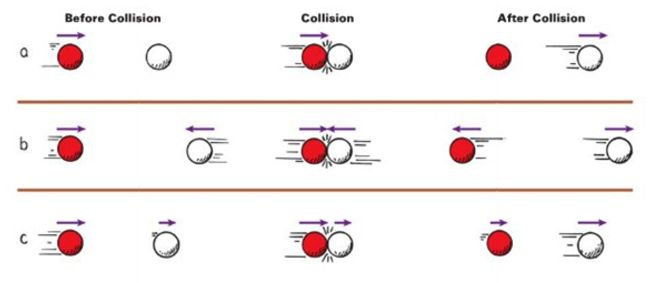
Objects rebound without lasting deformation or heat generation
Objects get tangled and/or generate heat
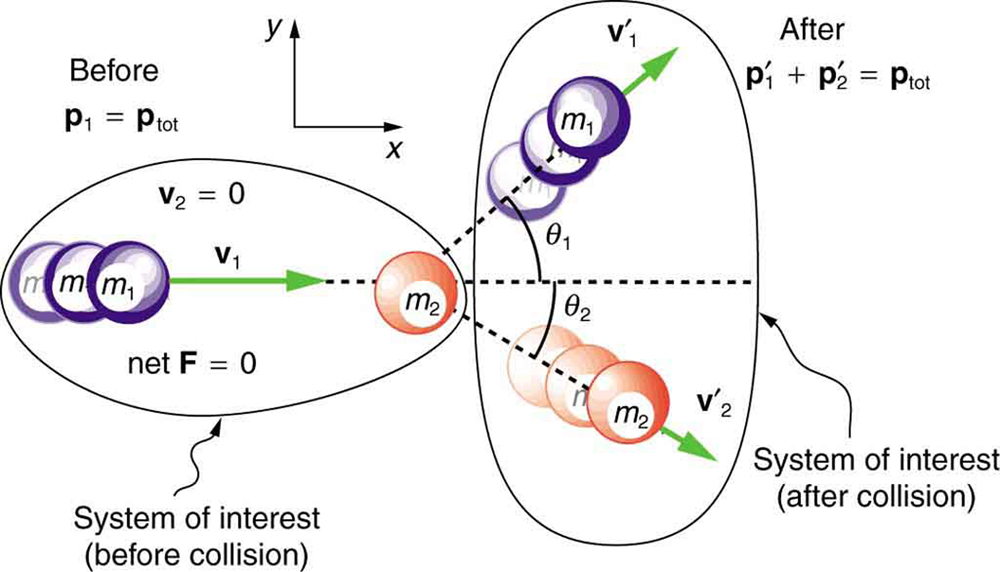
Collisions
Net momentum before collision = Net momentum after collision
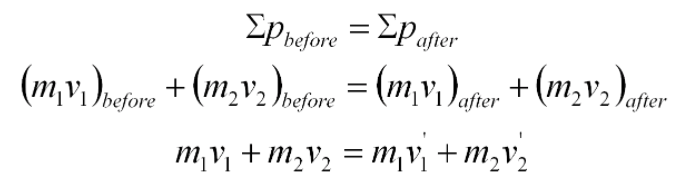
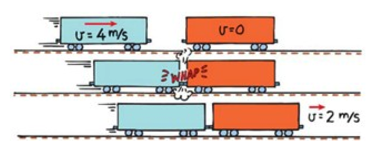
Checkpoint
What is the velocity of the blue truck after the collision?
5 m/s

Checkpoint
What is the velocity of grandma and grandson after the collision?
4 m/s
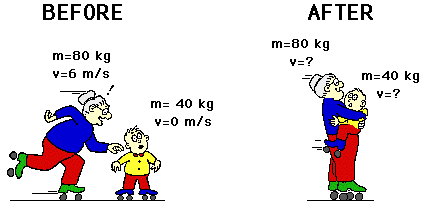
Momentum is a vector
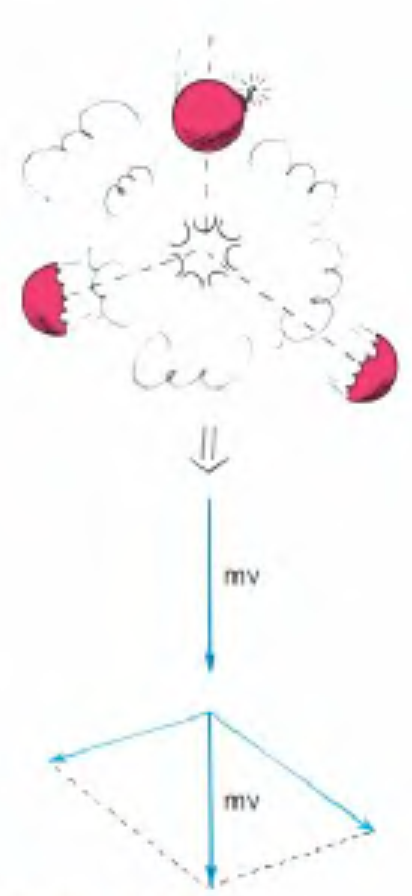
The sum of the momenta vectors is the same before and after the collision/explosion
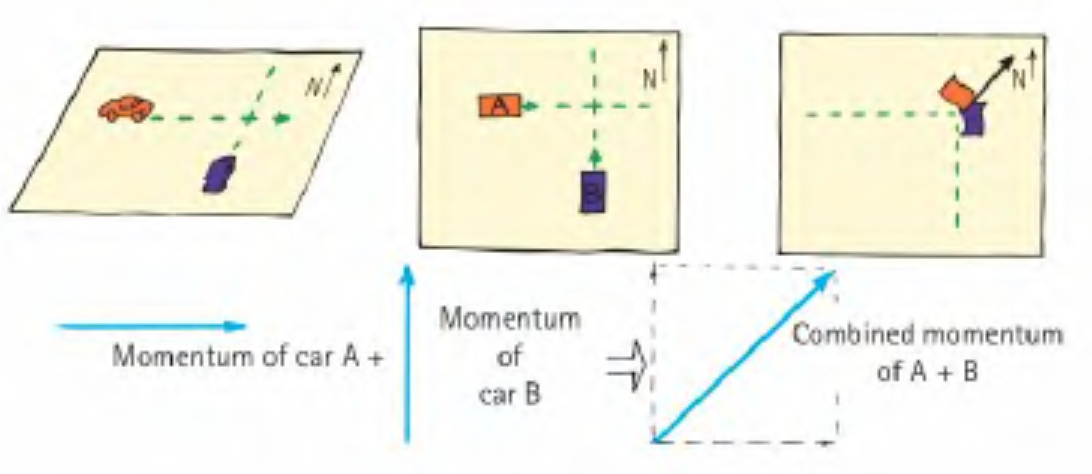
Conservation of Momentum in Two Dimensions
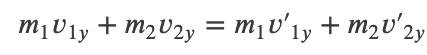
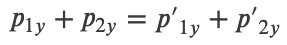
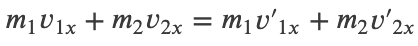
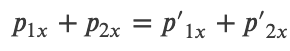
Momentum is conserved along each orthogonal dimension independently
Energy
Energy may be the most familiar concept in science, yet it is one of the most difficult to define

Here we are going to focus on Mechanical Energy: Work, Kinetic and Potential Energy
Work
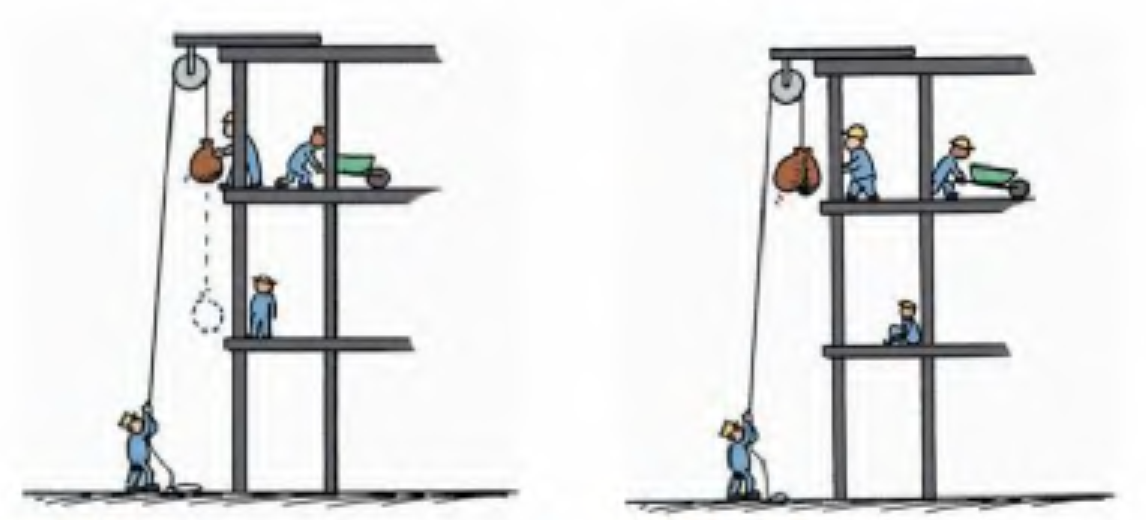
Work is proportional to force and distance
Work
Work is proportional to force and distance
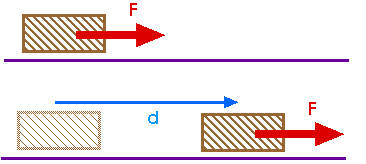
Work

The wall is not moving, so d = 0 and thus W = 0
Is he doing work on the wall?
Work
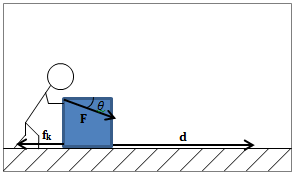
W = Fx d
Fx
Fy
Fy is not doing any work since the block doesn't move on the y direction
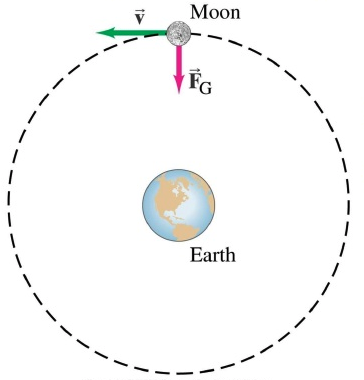
Is the Earth doing work on the Moon?
No because the force is not in the direction of motion
Checkpoint 1
Units of Work
Work has units of Energy
Work is Energy in transfer!
Checkpoint 2
How much work is needed to lift a bag of groceries that weights 300 N to a height of 2 m?
600 Joules
Power
1 horsepower = 746 watts
Power is the rate at which work is done.
Power is the rate at which energy is transferred!
Checkpoint 3
To lift a bag of groceries up the stairs in half the time you need ________ as much power?
Twice
With twice as much power you can do either the same work in half the time or twice as much work in the same time
Work-Energy theorem

The Floor is doing work on the bicycle, thus the bicycle's Energy must change (it decreases as it stops moving).
The Energy due to the bicycle's motion turns into heat
Kinetic Energy
The energy due to an object moving

Kinetic Energy
Potential Energy

The energy that is stored and held in readiness due to the position of an object (the arrow in this case)
Potential Energy -> Kinetic Energy

The Potential Energy of the arrow is converted to Kinetic Energy
Potential Energy
The energy that is stored and held in readiness due to the position of an object (the car in this case)
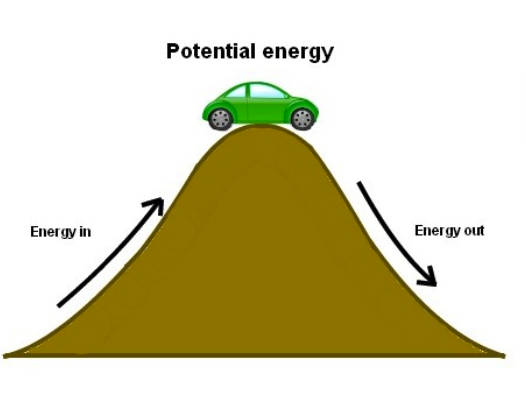
Work --> Potential Energy
Potential Energy --> Kinetic Energy
Gravitational Potential Energy
The potential energy of the ball is independent of how the ball got to its position, in all cases
PE = mg (3 meters)
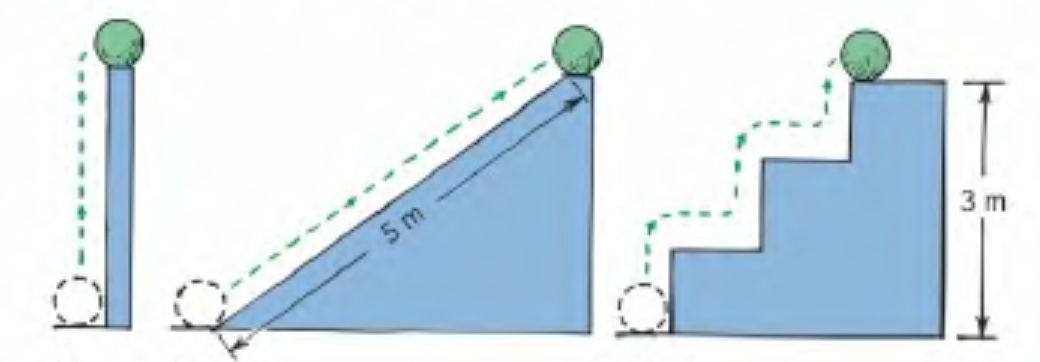
Gravitational Potential Energy = weight x height
h = 3 meters
The energy associated to the gravitational force and the work it does on objects
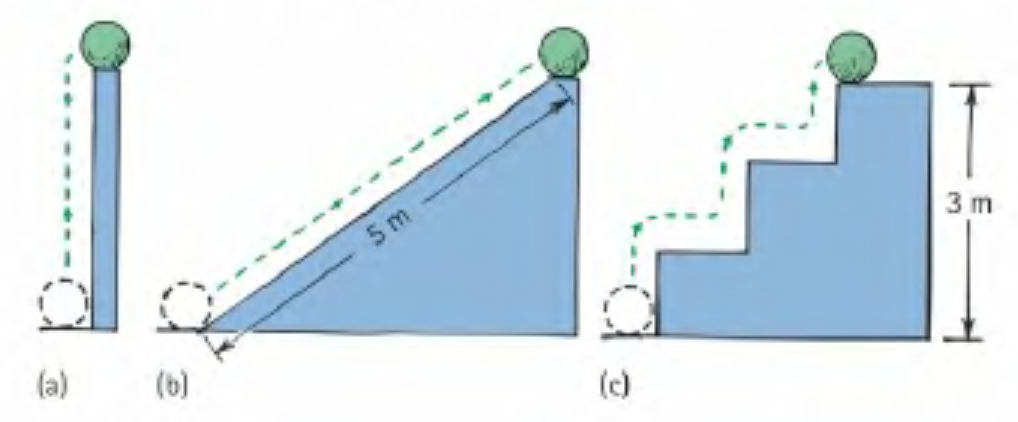
Checkpoint 4
Ignoring friction, which path requires the most work? (hint: remember that work is transfer of energy)
They all require the same amount of work =
Mechanical Energy
When the Potential Energy is gravitational:
Conservation of Energy
Energy cannot be created or destroyed: it may be transformed from one form into another, but the total amount of energy never changes
Conservation of Energy
When the Potential Energy is gravitational
In the absence of external work the mechanical energy of a systems remains constant

Conservation of Energy
The End
Copy of Momentum and Energy - Physics 2A
By Miguel Rocha
Copy of Momentum and Energy - Physics 2A
Physics 11
- 690



