Quantum Madness
M. Rocha
Physics 2B

Fasten your mind and make sure you don't loose it when we encounter quantum junctions
The first hints of a quantized world
- Plank's solution to the ultraviolet catastrophe (1900): the only way to explain blackbody radiation is by assuming that EM radiation energy is emitted in discrete chunks
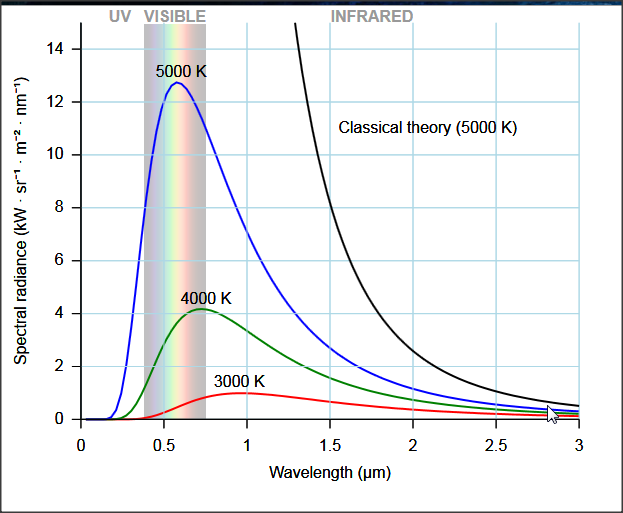
The first hints of a quantized world
- Einsteins's solution to the Photoelectric Effect (1905): Light itself must be quantized in order to explain why
3. Brightness affects the number of electrons emitted but not the electron's energy
Light must be particles (photons) with Energy = h f
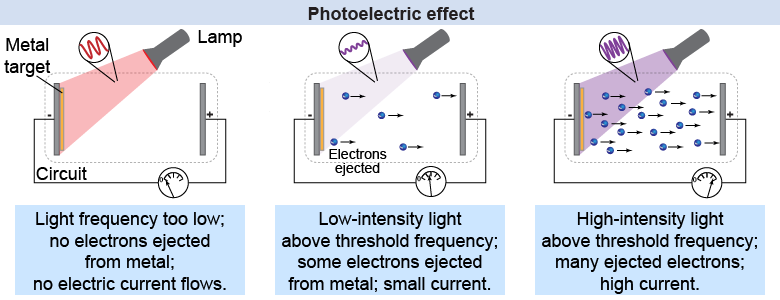
1. The effect is easy to observe with violet or ultraviolet light but not with red light (no matter the intensity/brightens)
2. The electron's energy depends on the frequency of light.
The first hints of a quantized world
- The Bohr model of the atom (1913): In order to explain the emission and absorption lines of atoms, the orbits of electrons must be restricted to discrete energy levels
The energy of the emmited/absorved photons corresponds to the energy difference between energy levels
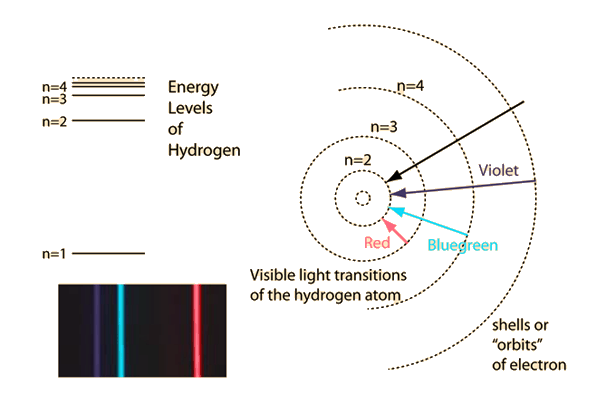
Plank's, Einstein's and Bohr's explanations of light and atomic phenomena via quantization were a paradigm shift, and left the world very puzzled with a lot of unanswered questions
Classical picture: smooth and continuous
Quantum picture: discrete and very blurry as of 1915
If light is made out of photons (particles) how do you explain diffraction?
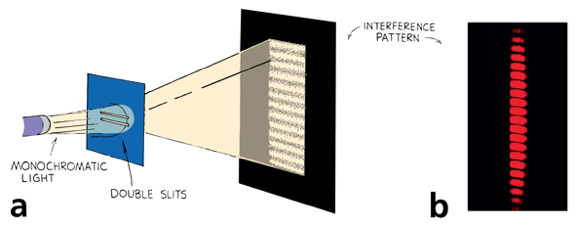
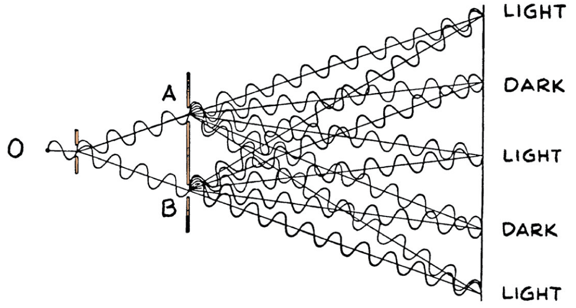
We relied on the wave properties of light to explain diffraction!

Double Slit Diffraction with Bullets?
Nope!
If light is made out of photons (particles) how you explain diffraction?


Diffraction occurs even on a photo by photon basis!
However if you were to close one slit the diffraction pattern does not occur!
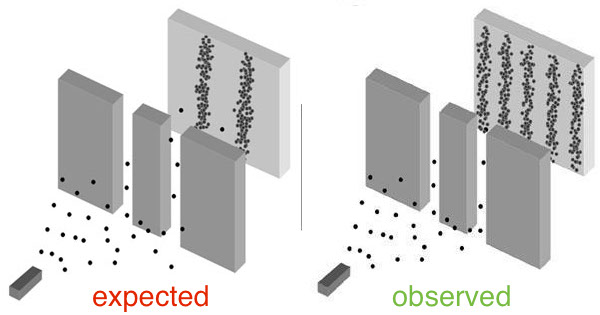
Double Slit Diffraction with Electrons?
Double slit diffraction occurs with electrons as well!
First evidence that electrons can behave as waves as well as particles

The Wave-Particle Duality
In order to explain the double slit experiments, both electrons and photons must have wave properties in an individual basis
A photon/electron behaves as a particle when it is being emitted by an atom or absorbed by photographic film or detector, and behaves as a wave in traveling from a source to the place where it is detected
The Wave-Particle Duality
Matter Waves
If matter particles behave like waves, then they must have a wavelength. In 1924 Louis de Broglie found that the wavelength of matter is given by Plank's constant divided by the momentum of the particle
Wavelength of matter waves
Checkpoint 1
What is the wavelength of a bullet of mass 0.02 kg traveling at 330 m/s ?
For comparison, the diameter of a hydrogen atom is 10^-10 m. The wavelength of a bullet is so small than diffraction effects are not measurable
The wavelength of an electron traveling at 2% the speed of light is about 10^-10 m. The electron's diffraction effects are measurable
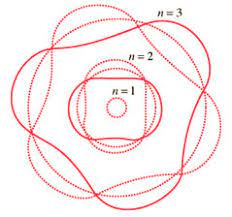
Explanation of Quantized Energy Levels
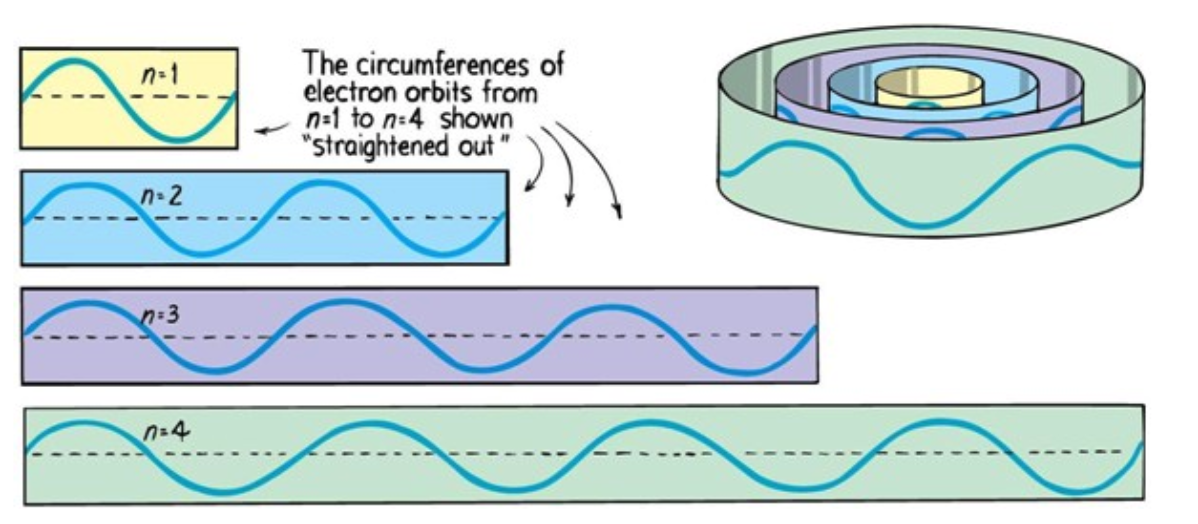
Electrons can only be at discrete energy levels (orbit radius), because the circumference of their orbit has to be an integer number of their wavelength in order to form standing waves, otherwise the experience destructive interference
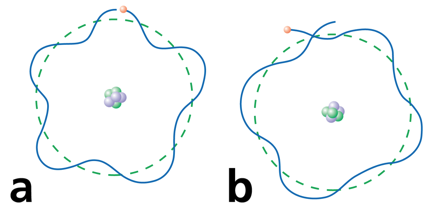
de Broglie's suggestion that electrons have a wavelength explained the quantized energy levels of atoms
The Schrodinger's Wave Equation
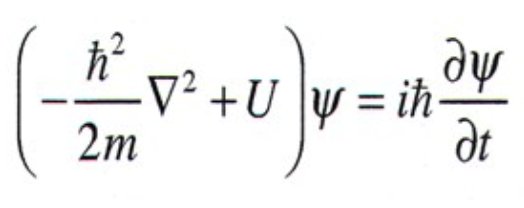
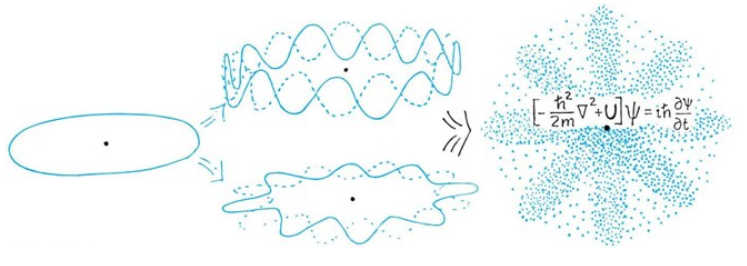
Schrodinger's equation describes the dynamics of quantum particles as the dynamics of probability waves. This is the base of quantum mechanics
Psi is what we call the wave function

Psi squared gives you the probability of finding a particle at some point
particle with low energy
particle with higher energy

The Wave Function of Electron's in a Hydrogen Ataom
Schrodingers Cat
The cat is both dead and alive until you open the box and the wave function collapses to only one state


Alive
Dead
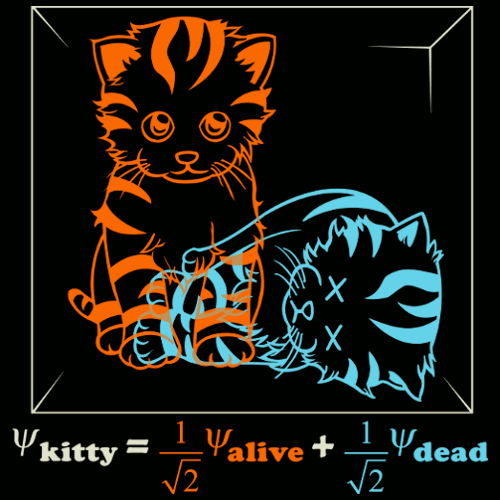
Heisenberg's Uncertainty Principle
High accuracy in position => large uncertainty in momentum
High accuracy in momentum => large uncertainty in position

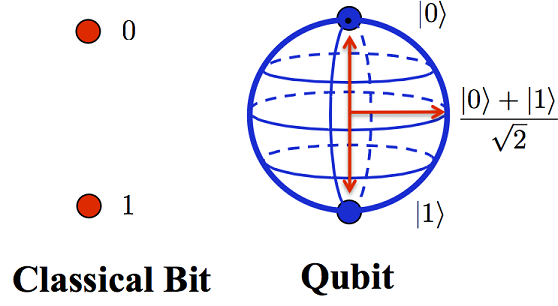
Quantum Entanglement

Quantum Computing
The End
The Bohr model of the atom is explained by de Broglie's equation
Copy of Quantum Physics (Physics 2B)
By Miguel Rocha
Copy of Quantum Physics (Physics 2B)
Physics 1 - Week 14 - Chapter 31-32
- 751



