Rotational Motion
M. Rocha
Physics 11
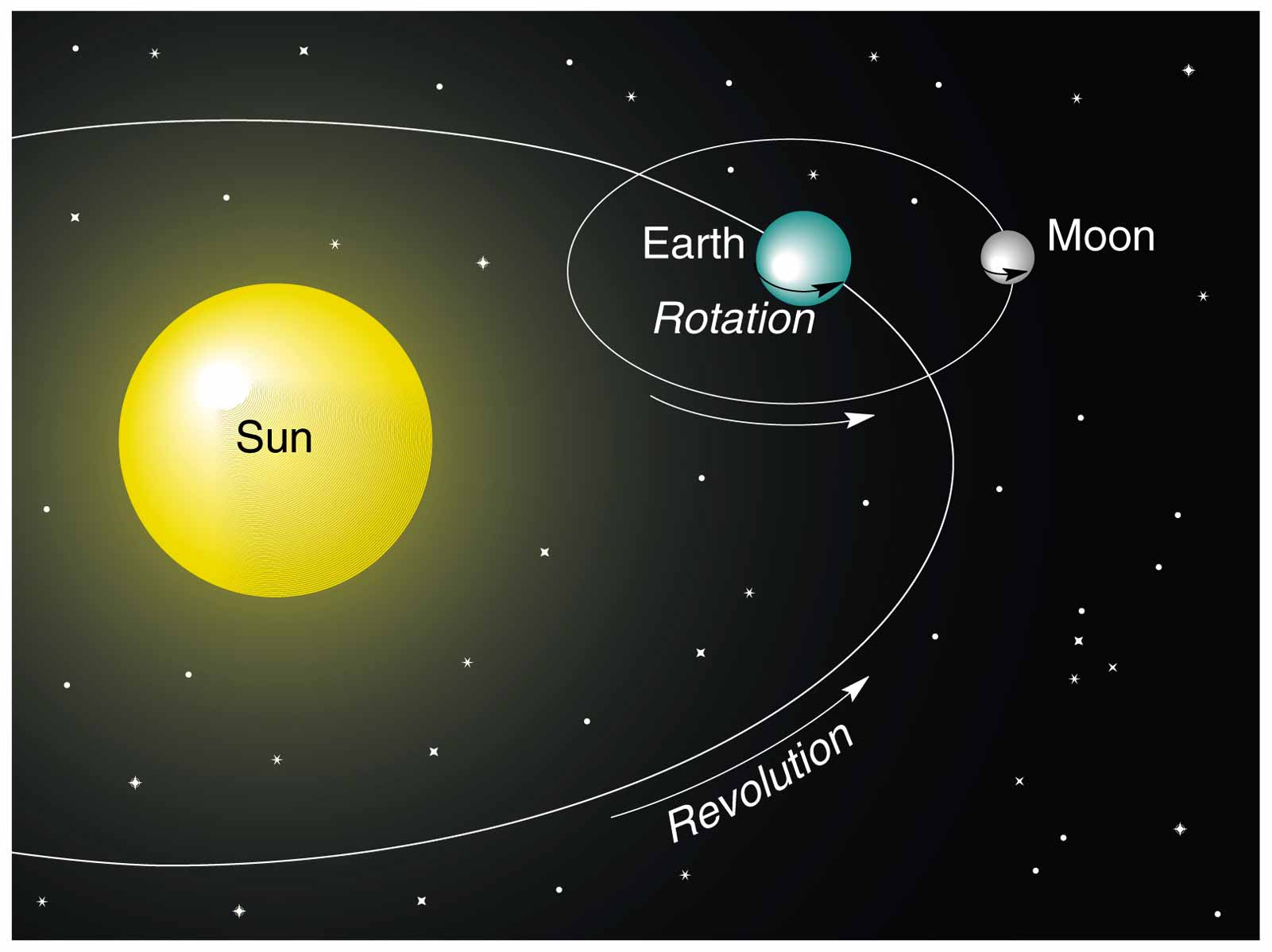
Rotation vs. Revolution
Rotation: when an object turns about an internal axis—that is, an axis located within the body of the object
Revolution: when an object turns about an external axis.
Rotation vs. Revolution
Angular Velocity
\mathrm{Angular \ Velocity} = \frac{\mathrm{Number \ of \ Rotations/Revolutions} }{ \mathrm{Time \ interval}}
\mathrm{Angular \ Velocity} = \omega = \frac{\mathrm{radians}}{t}
RPMs (Revolutions/Rotations per minute) is a commonly used measure of angular velocity
In Physics we like to use "radians per unit time" as a measure of angular velocity
2 \pi \ \mathrm{radians} = \mathrm{1 \ full \ circle }
L = \theta \times r
Small angle approximation
Arc Length =
r \sin \theta \approx r \ \theta
\approx
r = Hypotenuse
Adjacent
Arc Length and The Small Angle Approximation
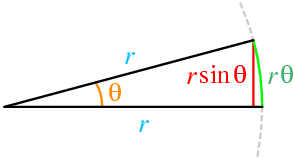
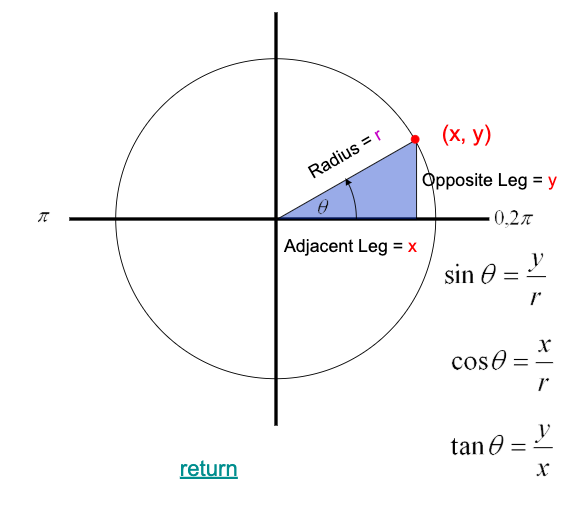
Circle Trigonometry
\pi = 180^{\circ}
\pi/2 = 90 ^{\circ}
3\pi/2 = 270^{\circ}
2\pi = 360^{\circ}
\pi =\frac{\mathrm{Circunference}}{\mathrm{Diameter}} = \frac{\mathrm{Circunference}}{2 \times \mathrm{Radius}}
Checkpoint 1
\omega = \frac{\mathrm{radians}}{t}
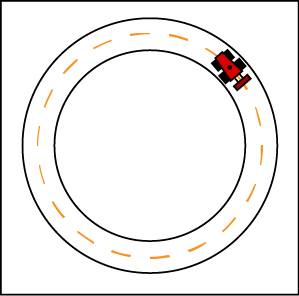
If a race car travels around a circular track with an angular velocity of , how long does it takes to complete a full revolution.
\omega = \pi \ \mathrm{radians/min}
2 minutes
2 \pi \ \mathrm{radians} = \mathrm{1 \ full \ circle }
r
Tangential Velocity
Vt
Tangential velocity is the linear velocity of something moving along a circular path
v_\mathrm{tangential} = \omega \times r
If angular velocity is given in radians, then
v_\mathrm{tangential} = \frac{\mathrm{arc \ length}}{\mathrm{time}}
= r \ \theta
\theta \mathrm{\ in \ radians}
Checkpoint 2
\omega = \frac{\mathrm{radians}}{t},
If car 1 and car 2 below travel on a circular track with the same angular velocity, which one has a larger tangential velocity and by how much?
Car 1 travels 2x faster
v_t = \omega \times r
car 2
2r
car 1
r
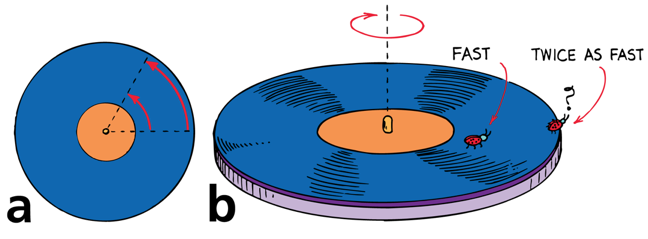
Tangential Velocity
All parts of the turntable rotate at the same angular velocity
A point farther away from the center travels a longer path in the same time and therefore has a greater tangential velocity
Rotational Inertia
Inertia: The tendency of an object to resist changes in velocity. An object at rest tends to stay at rest and an object in motion tends to remain moving in a straight line.
Rotational Inertia: The tendency of a rotating object to resist changes in angular velocity. An object rotating about an axis tends to remain rotating about the same axis unless interfered with by some external force.
Rotational Inertia
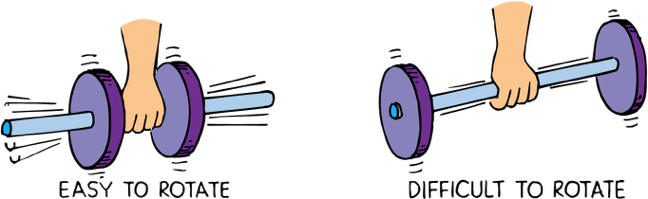
Rotational Inertia depends on the amount of mass and the distance of mass from the axis of rotation
Rotational Inertia
The longest the pole the more balance it provides
Rotational Inertia depends on the amount of mass and the distance of mass from the axis of rotation
Rotational Inertia
Rotational Inertia depends on the amount of mass and the distance of mass from the axis of rotation
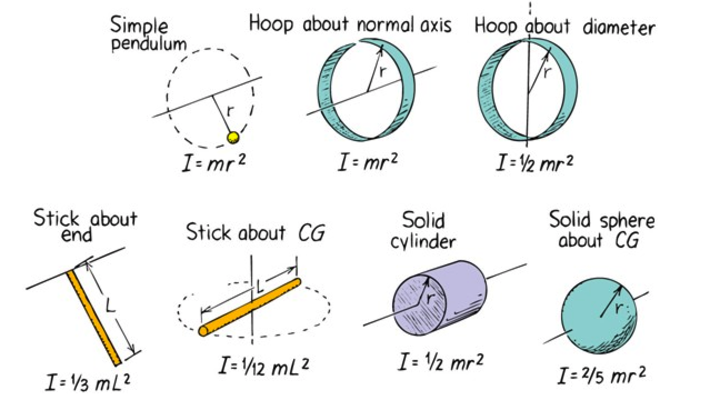
Checkpoint 3
For an ice skater rotating, which body positioning has the greatest rotational inertia
d) has the most amount of mass distant to the axis of rotation, so it has the highest rotational intertia
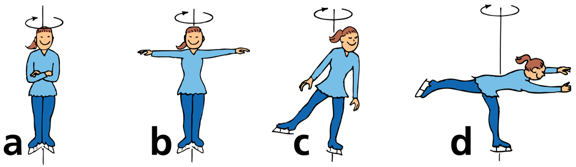
Consider balancing a hammer upright on the tip of your finger. The end is heavier than the handle. Which way is it easier to balance? a) with the head at the top, or b) the other way around.
a) With the head at the top.
That way the rotational inertia is the greatest so it will be harder for it to rotate about your finger.
b)
a)
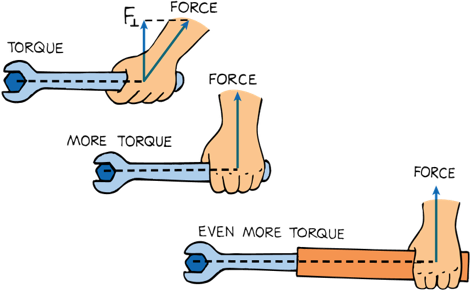
Torque
You know that a longer lever arm makes it easier to rotate objects that require a lot of rotational force
Torque
Torque is rotational force. It is proportional to the applied tangential force and the distance to the axis of rotation.
\mathrm{Torque} = \mathrm{Force} \times \mathrm{lever \ arm \ length} = F \times r
Angular Acceleration
A force causes a change in velocity, i.e. acceleration (Newton's 2nd law)
\mathrm{Angular \ Acceleration} = \frac{\mathrm{Torque}}{\mathrm{Rotational \ Inertia}} = \frac{ F \times r}{I}
A torque causes a change in angular velocity, i.e. angular acceleration (Newton's 2nd law in rotational motion)
a = \frac{F}{m}
Balanced Torques
\sum{\mathrm{Torques}} = 0 \Rightarrow \mathrm{No \ rotation}
(F \times r)_\mathrm{counter \ clockwise} - (F \times r)_\mathrm{clockwise} = 0
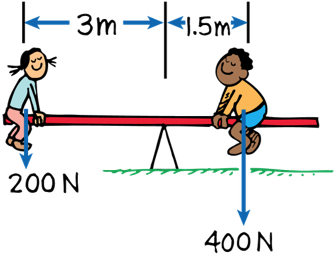
Checkpoint 4
If the system below is balanced (not rotating), what is the weight of the block hung at the 10-cm mark?
15 N
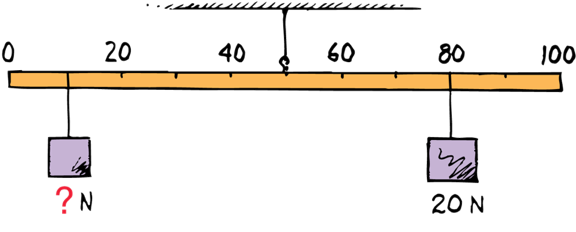
Angular Momentum
Angular Momentum is rotational inertia in rotational motion
\mathrm{Momentum} = \mathrm{mass} \times \mathrm{velocity}
p = mv
Momentum is inertia in motion
\mathrm{Angular \ Momentum} = \mathrm{rotational \ inertia} \times \mathrm{rotational \ velocity}
\mathrm{Angular \ Momentum} = I \omega
Angular Momentum
Angular Momentum is rotational inertia in rotational motion
\mathrm{Angular \ Momentum} = \mathrm{rotational \ inertia} \times \mathrm{rotational \ velocity}
\mathrm{Angular \ Momentum} = I \omega
For a point mass
I \omega = m r^2 \omega = m r^2 \frac{v}{r} = m v r
I = m r^2 ,
\omega = \frac{v}{r}
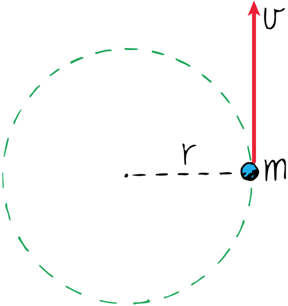
Conservation of Angular Momentum
If no external net torque acts on a rotating system, the angular momentum of that system remains constant.
Conservation of Angular Momentum
If no external net torque acts on a rotating system, the angular momentum of that system remains constant.
Conservation of Angular Momentum
If no external net torque acts on a rotating system, the angular momentum of that system remains constant.
Centripetal Force
Centripetal force is the force that keeps objects in circular motion
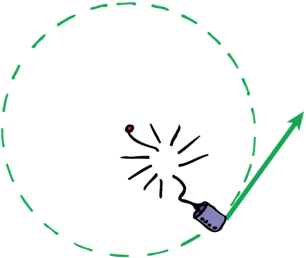
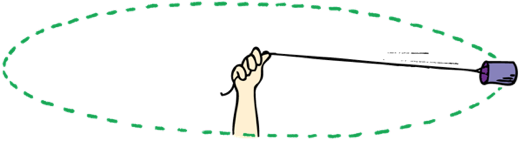
Centripetal Force
Centripetal force always points to the center and its magnitude is
F_{c} = \frac{mv_{t}^2}{r}
F_{c}
Centripetal Force
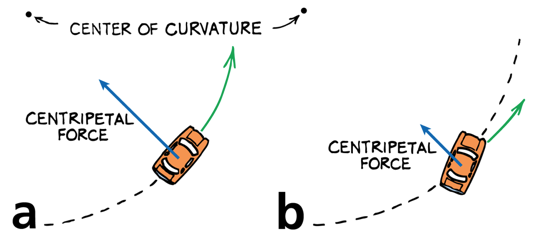
Centripetal force holds a car in a curved path.
a) For the car to go around a curve, there must be sufficient friction to provide the required centripetal force.
b) If the force of friction is not great enough, skidding occurs.
Checkpoint 5
F_{c} = \frac{mv_{t}^2}{r}
A car with mass m = 1000 kg takes a turn with a radius of curvature of r = 30 m at a speed of v = 30 m/s (about 65 miles/h) , if the force of friction between the tires and the road is 7000 N, would it make the turn?
F_{c} = \frac{mv^2}{r} = \frac{1000kg \times (30 m/s)^2}{30m} = 30000 N
No, it will skid
Centripetal Force vs. Centrifugal Force
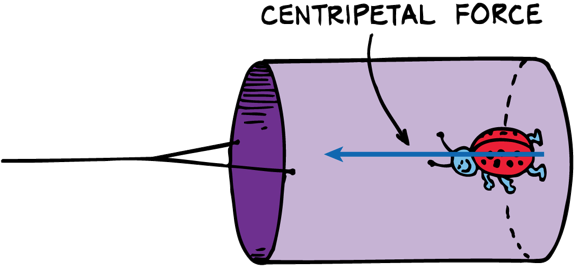
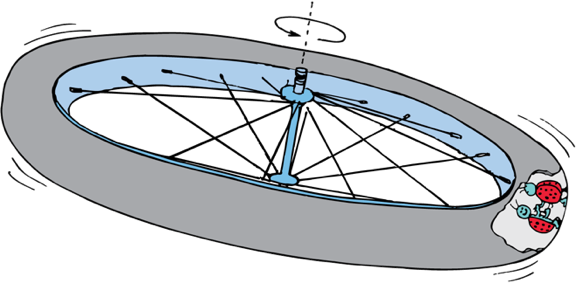
The only force that is exerted on the whirling can (neglecting gravity) is directed toward the center of circular motion. This is a centripetal force. No outward force acts on the can
Centripetal Force v.s. Centrifugal Force
However from the reference frame of the lady bug it feels like there is a centrifugal force away from the center, and the centripetal force is just a support force
Centrifugal Force
Centripetal Force v.s. Centrifugal Force
The apparent centrifugal inside a rotating reference frame feels just like gravity, we can call this simulated gravity
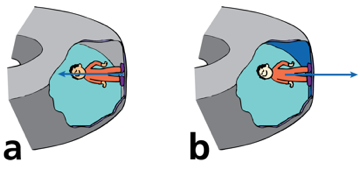
a) As seen from the outside, the only force exerted on the man is by the floor
b) As seen from the inside, there is a fictitious centrifugal force that simulates gravity
Simulated Gravity
Rotational Motion
By Miguel Rocha
Rotational Motion
Physics 11
