Waves and Sound
M. Rocha
Physics 10
Vibrations Rule the Universe
Vibrations
A repeating back-and-forth motion about an equilibrium position is a vibration (a.k.a. oscillations)
Period
Amplitude
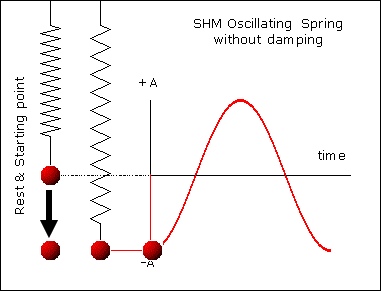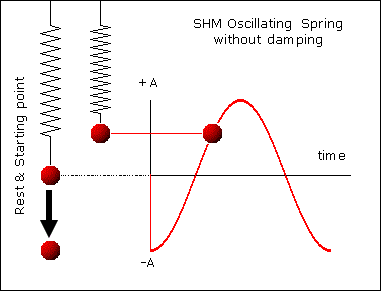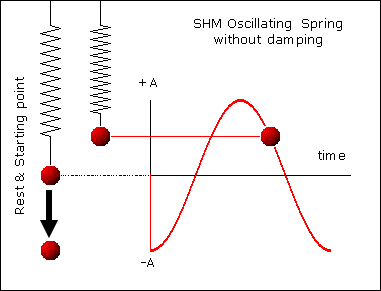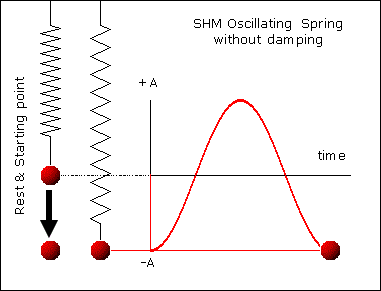
Vibrations
The time required for a full oscillation (one round trip)
Period:
Frequency:
Number of oscillations per unit time
\mathrm{Frequency} = \frac{1}{\mathrm{Period}}
Unit of Frequency: 1 Hertz = [1/second] (1 oscillation per second)
For example, for a period of 2 seconds per oscillation, the frequency is ½ oscillations per second or ½ Hertz
The Pendulum
An ideal pendulum (no friction) would oscillate forever with the same period and amplitude
The Pendulum
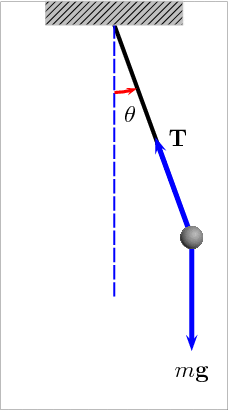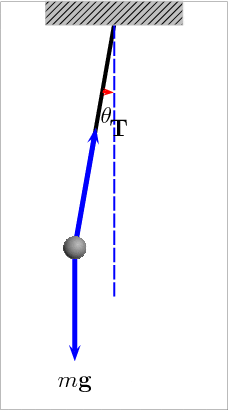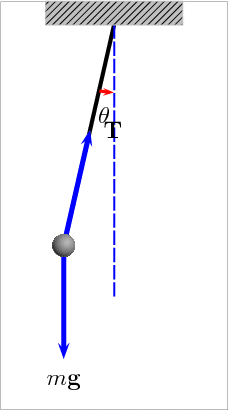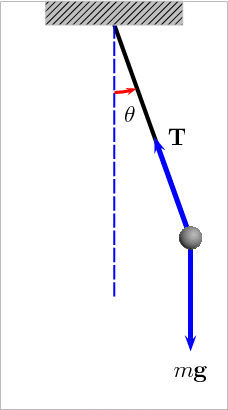
For small amplitudes a pendulum's period only depends on its length because the acceleration due to gravity is independent of the object's mass
T= 2 \pi \sqrt(\frac{L}{g})
The Pendulum
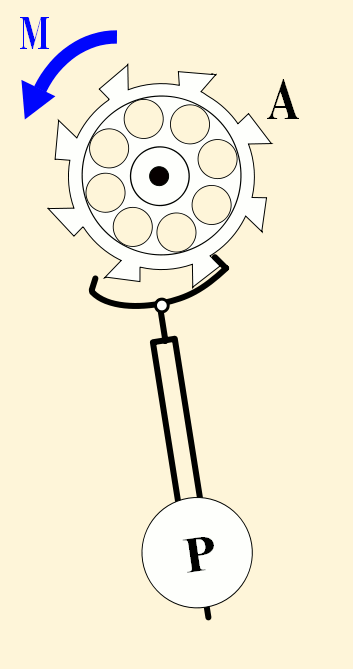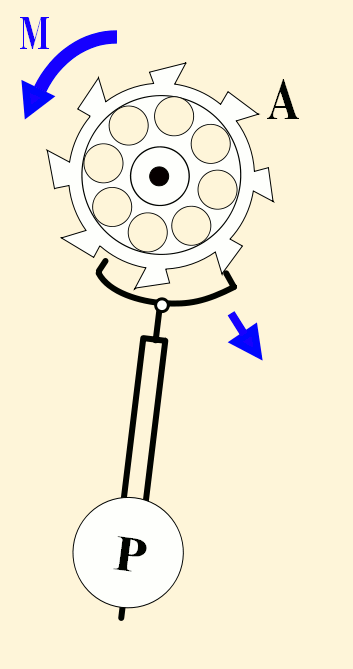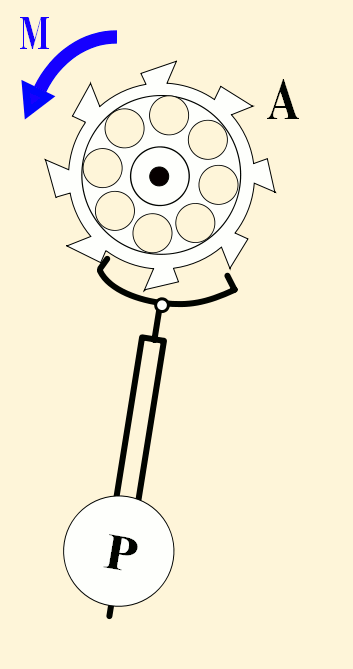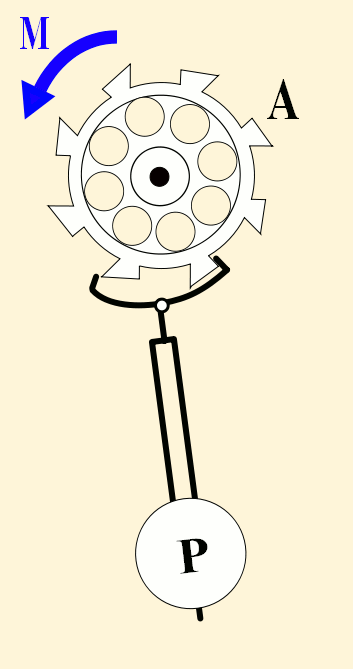
Pendulums swing back and forth with such regularity that they have long been used to control the motion of clocks
Checkpoint 1
A pendulum oscillates with a period of 2 seconds. How long would it take to do a round trip if we increase the length of the rope by 4 times?
T= 2 \pi \sqrt(\frac{L}{g})
2 \ \mathrm{seconds} \times \sqrt{4} = 4 \ \mathrm{seconds}
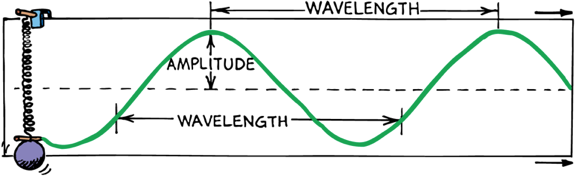
Waves
Vibrations create waves. A sine curve is a pictorial representation of a wave
Waves
Vibrations are the source of all waves
For example electrons in the antenna of an AM radio station at 960 kHz vibrate 960,000 times each second, producing 960 kHz radio waves
Transverse Waves
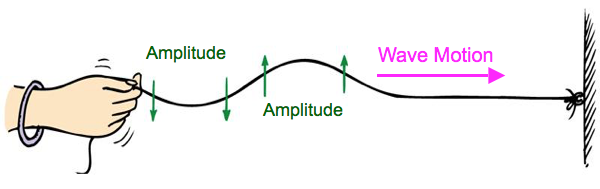
For transverse waves the wave’s amplitude is perpendicular to the wave’s motion
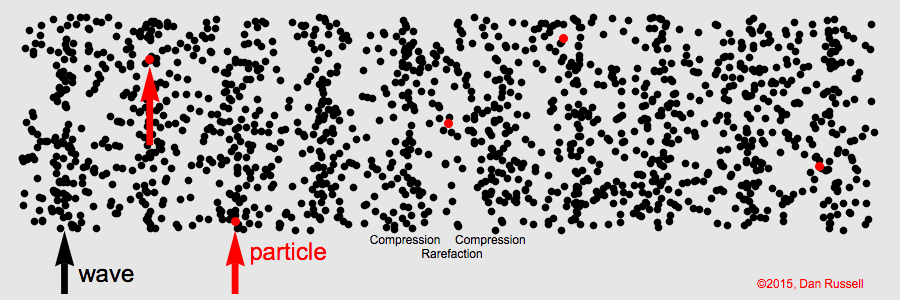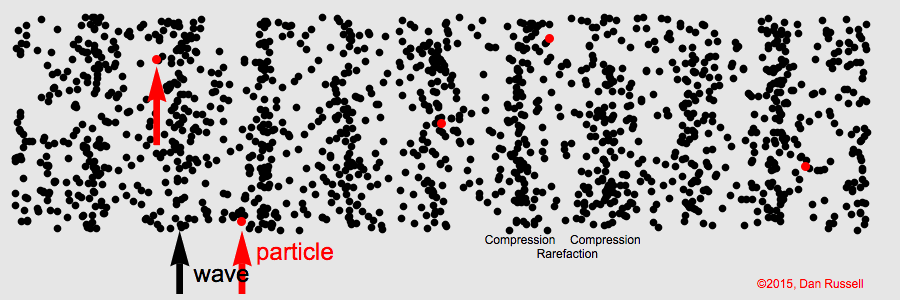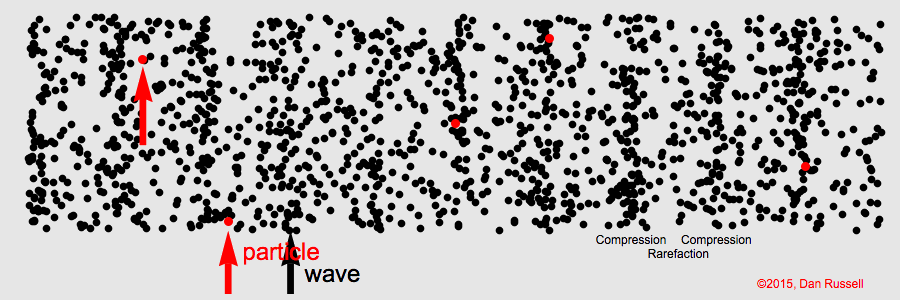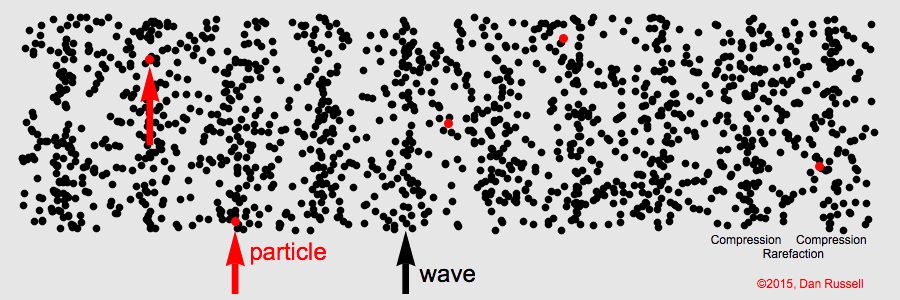
Longitudinal Waves
For longitudinal waves the wave’s amplitude is parallel to the wave’s motion
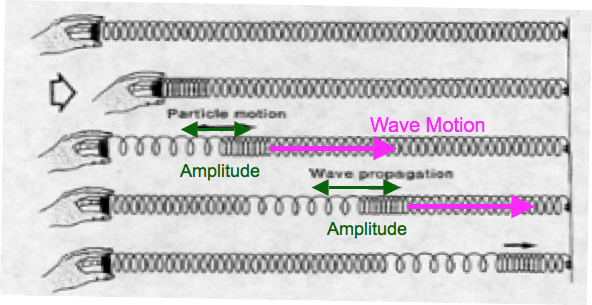
Waves transport energy without a net displacement of the medium they travel on
Transverse Waves
Waves transport energy without a net displacement of the medium they travel on
Longitudinal Waves
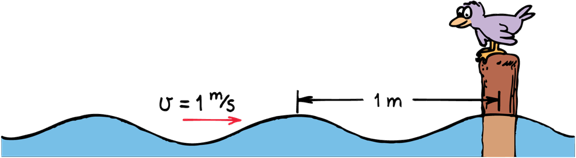
The speed at which waves travel through a medium is related to the frequency and wavelength
Wave Speed
\mathrm{Wave \ Speed} = \frac{\mathrm{Wave \ Length}}{\mathrm{Period}} = \mathrm{Frequency} \times \mathrm{Wave \ Length}
Checkpoint 2
What is the Frequency and Period of a wave set traveling at 6 m/s with a wave length of 3 m ?
\mathrm{Frequency} = \frac{\mathrm{Wave \ Speed}}{\mathrm{Wavelength}} = \frac{6 \ m/s}{3 \ m} = 2 \ \mathrm{per} \ s
\mathrm{Wave \ Speed} = \mathrm{Frequency} \times \mathrm{Wave \ Length}
= \frac{\mathrm{Wave \ Length}}{\mathrm{Period}}
\mathrm{Period} = \frac{\mathrm{Wavelength}}{\mathrm{Wave \ Speed}} = \frac{3 \ m}{6 \ m/s} = \frac{1}{2} s
Wave Interference
Multiple waves can share the same space at the same time, this is called interference
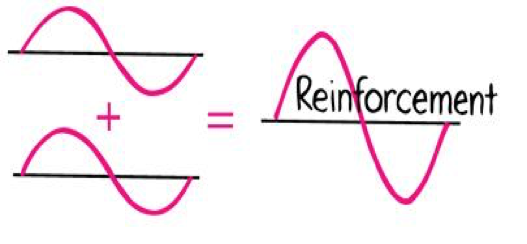
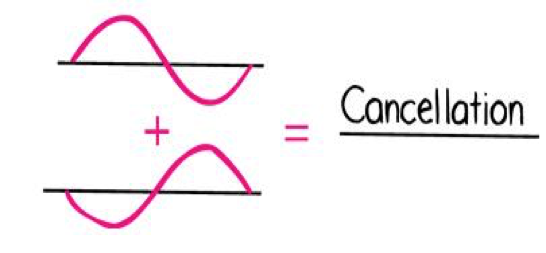
Constructive Interference
Destructive Interference
Waves in phase
Waves out of phase
Wave Interference
Wave Interference
Noise-canceling headphones use a microphone that listens for noise and a speaker that produces the same noise but out of phase (destructive interference)
Wave Interference
Standing Waves
\lambda = \mathrm{Wavelenght}
Wave Interference in 2D
Standing Waves in 2D
Doppler Effect
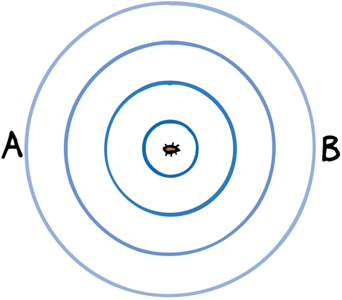
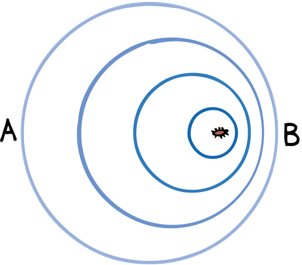
When the source of waves moves the frequency increases in front of the source and decreases behind the source
At point A the frequency is lower than at point B
Source not moving
Source Moving
At point A the frequency is the same than at point B
Doppler Effect
When the source of waves moves the frequency increases in front of the source and decreases behind the source
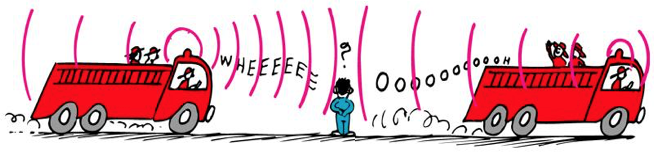
If moving towards you, wavelength shorter and frequency higher.
If moving away, wavelength longer and frequency lower.
Doppler Effect
When the source of waves moves the frequency increases in front of the source and decreases behind the source
Police use the Doppler effect of radar waves to measure the speeds of cars on the highway.
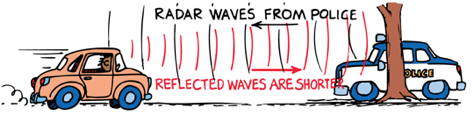
Doppler Effect
When the source of waves moves the frequency increases in front of the source and decreases behind the source
Astronomers use the Doppler effect to measure the rotation speed of galaxies.
Sound and Music
Origin of Sound
Sound is a wave that is produced by the vibrations of material objects
Nature of Sound
Sound in air is a longitudinal wave created by compressions and rarefactions
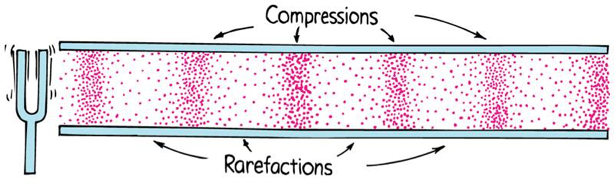
Sound Needs a Material Medium to Travel
Sound cannot travel in vacuum
Media That Transmit Sound
Sound travels faster in liquids and solids than in gasses (air)
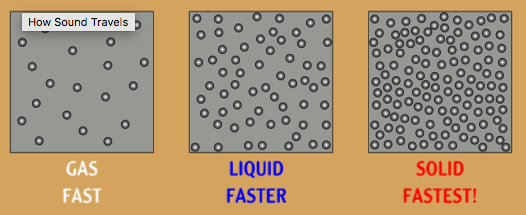
The closer the molecules are and the more elastic the material is, the better sound travels
Media That Transmit Sound
Sound travels faster in liquids and solids than in gasses (air)
The closer the molecules are and the more elastic the material is, the better sound travels
Speed of Sound
Air 20°C
Water 20°C
Metal 20°C
The speed of sound depends on temperature, the faster the molecules move (the higher the temperature) the faster sound travels
1484 m/s
5120 m/s
343 m/s
Light is a million times faster than sound on air
Speed of Sound
Light Speed: ~3x10^8 m/s
Sound Speed: ~3.5x10^2 m/s
Checkpoint 1
If the speed of sound on air is about 340 m/s, and you hear a thunder 3 s after you see it, how far away is the storm?
About 1000 m = 1 km
Loudness and Amplitude
Loudness depends on amplitude of pressure and density variations in sound waves
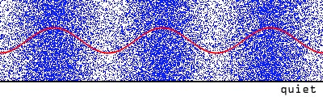
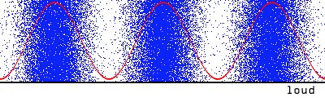
Loudness Scale
Loudness is measured in Decibels (dB), which is a logarithmic scale
Decibels Scale
B_1 - B_2 = 10 \log_{10}(\frac{I_1}{I_2})
=> 10^\frac{B_1 - B_2}{10} = \frac{I_1}{I_2}
A subway train is 50 db louder than a conversation. Thus it is
10^\frac{50}{10} = 10^5 = 100000
more intense. The amplitude/energy of the sound of a subway is 100000 greater than that of a conversation
Checkpoint 2
What is the intensity/amplitude difference between sound waves from normal speech at 60 dB, and sound waves from a loud concert at 120 dB?
Difference in dB scale = 120 dB - 60 dB = 60 dB
Difference in intensity = 10^(60/10) = 10^6 = 1000000
10^\frac{B_1 - B_2}{10} = \frac{I_1}{I_2}
Sound Reflection
Soft surfaces absorb sound
Is quiet after a fresh snowfall because soft snow absorbs sound
Symphony halls use hard plates to reflect sound and produce reverberation
Sound reflects strongly from rigid surfaces
Natural Frequency
All objects have a natural frequency at which they vibrate if they are struck
The natural frequency of an object depends on shape and composition
Music
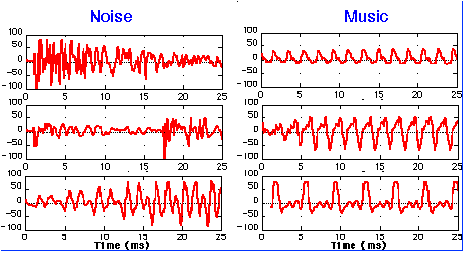
Musical Notes
Musical notes correspond to specific frequencies
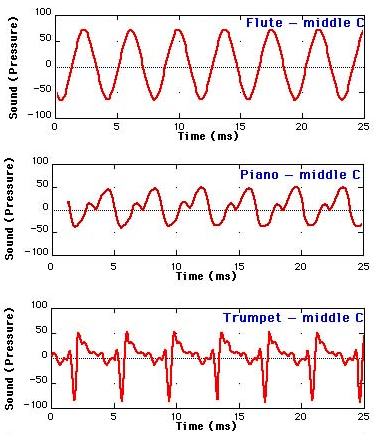
Middle C has the same fundamental frequency of 262Hz when played in different instruments
Musical Notes
Pythagoras discovered that different musical notes were related by mathematical ratios, such as the ratios of lengths or sizes in musical instruments or even in simple objects
The note produced by two strings, one half the length of the other, sounded similar
In Western music these two notes are said to be an octave apart
Notes and Frequencies
An octave has 12 steps and going up an octave doubles the frequency
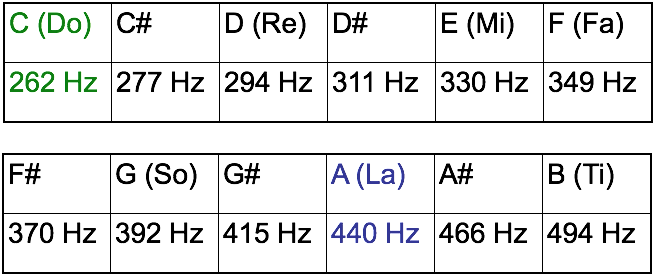
C
524 Hz
After 12 steps you get back to C: Same not but double the frequency (one octave apart)
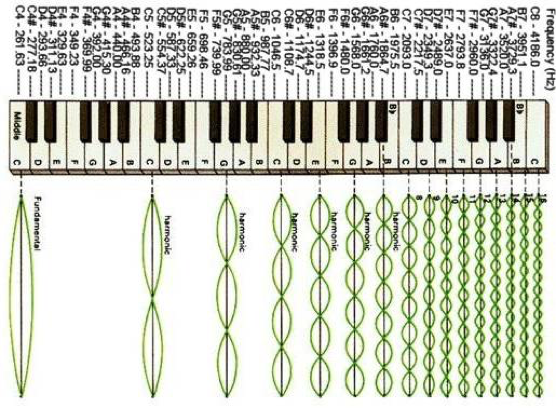
Piano Keyboard (Upper Half)
Woodwind Instruments
Resonant standing waves also produced in a pipe, but the pipe length varied by air holes (finger-holes, keys, or pads)
The End
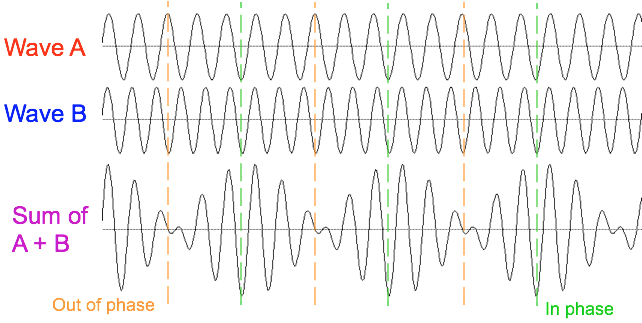
Beats
When the two frequencies are almost the same, the sum is about the same frequency but periodically varying amplitude. This is called a beat
Beats
When the two frequencies are almost the same, the sum is about the same frequency but periodically varying amplitude. This is called a beat
Same effect seen with two combs with different tooth spacing.
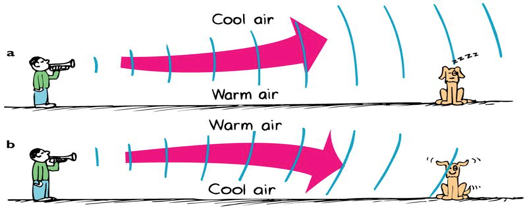
Sound Refraction
Sound speed can vary by material or conditions.
This causes the sound to bend in direction, in the same way that light bends when it passes through a glass lens
Resonance
Resonance occurs when forced/induced vibrations match an object’s natural frequency
Resonance dramatically increases the amplitude
Resonance
Resonance occurs whenever successive impulses are applied to a vibrating object in rhythm with its natural frequency
Resonance dramatically increases the amplitude
Resonance dramatically increases the amplitude
Resonance dramatically increases the amplitude
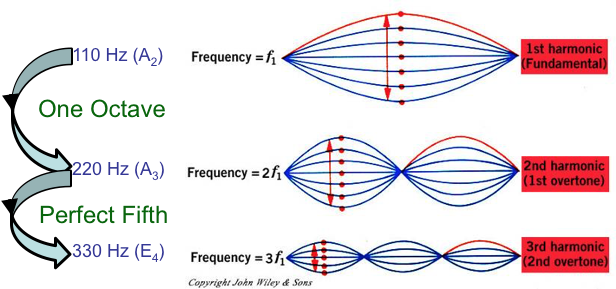
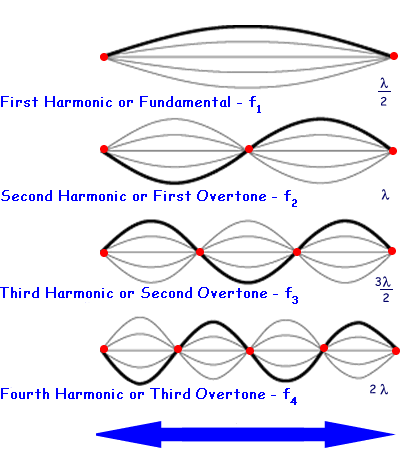
The Fundamental is the lowest frequency standing wave. The Overtones are twice, three times, etc., the frequency of the Fundamental
Fundamental and Overtones
Waves and Sound - Physics 10
By Miguel Rocha
Waves and Sound - Physics 10
Physics 1 - Week 8 - Chapters 19-21
