Coordenadas anatómicas e introducción a la navegación quirúrgica
BE3027 - Robótica Médica
¿Qué tenemos hasta ahora?
Import and Spatial Referencing
Display, Volume Rendering, and Surfaces
Preprocessing and Augmentation
GroundTruth Labeling and Segmentation
Adquisición y reconstrucción
Análisis y/o aplicación
un poco de esto
(aunque faltan más detalles)
Import and Spatial Referencing
Display, Volume Rendering, and Surfaces
Adquisición y reconstrucción
un poco de esto
(aunque faltan más detalles)
Preprocessing and Augmentation
GroundTruth Labeling and Segmentation
Análisis y/o aplicación
nos enfocaremos primero en estos
DICOM
NifTI
NRRD
Analyze
Minc
Adquisición, almacenamiento, intercambio y transmisión
Digital Imaging and Communications in Medicine (DICOM)
tutorial para trabajar con DICOM en 3D Slicer
https://spujol.github.io/SlicerDICOMTutorial/3DSlicer_DICOMTutorial_SoniaPujol.pdf
Interpretando la información espacial
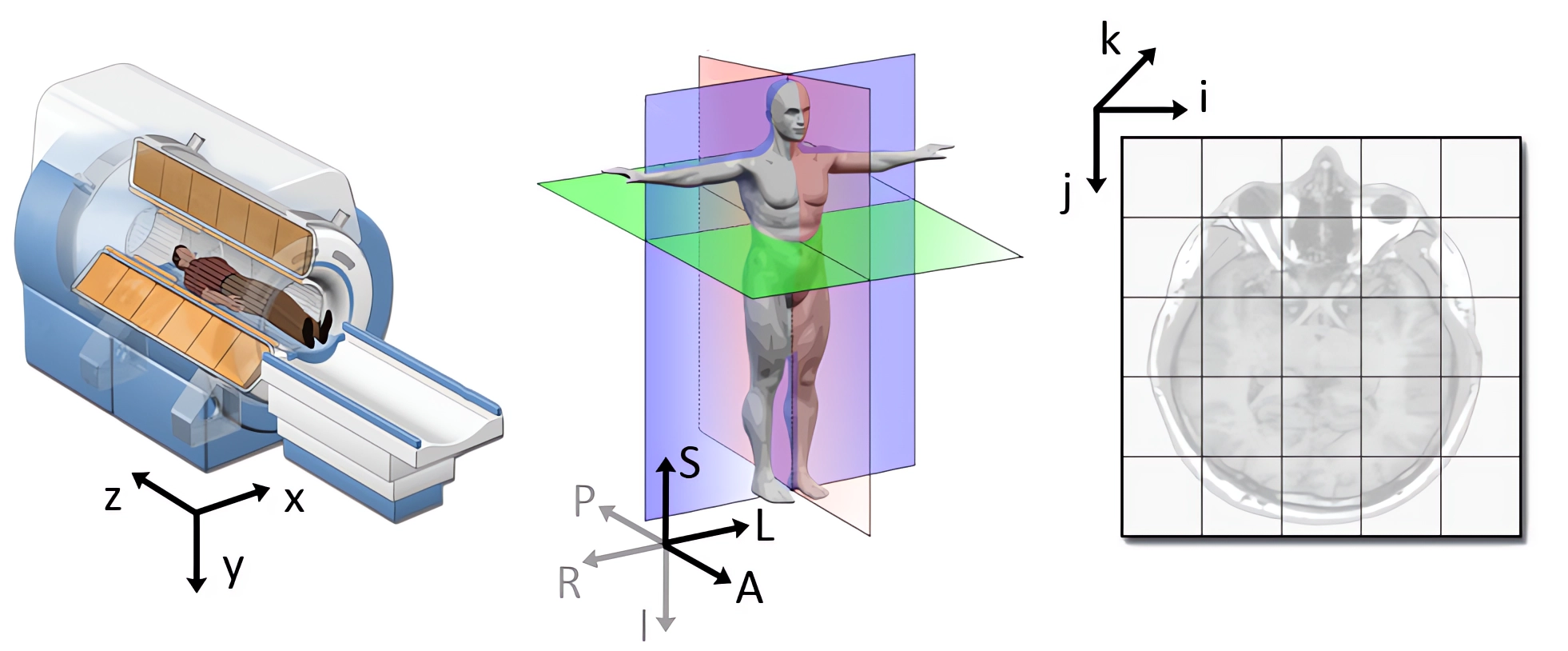
coordenadas del mundo (inerciales) [m]
coordenadas anatómicas (del paciente) [mm]
coordenadas intrínsecas (de imagen) [px] | [voxel]
xyz
LPS
RAS
ijk
la selección del origen es arbitraria, aunque típicamente se coloca en el centro de rotación (COR) del sistema pero depende del fabricante
\{W\}
coordenadas del mundo (inerciales) [m]
coordenadas anatómicas (del paciente) [mm]
coordenadas intrínsecas (de imagen) [px] | [voxel]
xyz
LPS
RAS
ijk
dos convenciones:
LPS (Left, Posterior, Superior)
RAS (Right, Anterior, Superior)
\{W\}
\{A\}
sagital
coronal
transversal
sagital
coronal
transversal
convención RAS
- NifTI
- General Electric
- 3D Slicer
convención LPS
- DICOM
- Siemens y el resto
- MATLAB
sagital
coronal
transversal
convención RAS
- NifTI
- General Electric
- 3D Slicer
convención LPS
- DICOM
- Siemens y el resto
- MATLAB
\begin{bmatrix} R \\ A \\ S \end{bmatrix}=\begin{bmatrix} -L \\ -P \\ S \end{bmatrix}
\begin{bmatrix} R \\ A \\ S \end{bmatrix}=\mathbf{R}_z(\pi)\begin{bmatrix} L \\ P \\ S \end{bmatrix}
coordenadas del mundo (inerciales) [m]
coordenadas anatómicas (del paciente) [mm]
coordenadas intrínsecas (de imagen) [px] | [voxel]
xyz
ijk
LPS
RAS
\{A\}
\{S\}
\{W\}
\{A\}
\{S\}
\{W\}
coordenadas del mundo (inerciales) [m]
coordenadas anatómicas (del paciente) [mm]
coordenadas intrínsecas (de imagen) [px] | [voxel]
xyz
ijk
LPS
RAS
De coordenadas intrínsecas a anatómicas
\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}=
\begin{bmatrix} \mathbf{B} & \mathbf{C} & \mathbf{B} \times \mathbf{C} & \mathbf{T} \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} \Delta x & 0 & 0 & 0 \\ 0 & \Delta y & 0 & 0 \\ 0 & 0 & \Delta z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} i \\ j \\ k \\ 1 \end{bmatrix}
De coordenadas intrínsecas a anatómicas
\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}=
\underbrace{\begin{bmatrix} \mathbf{B} & \mathbf{C} & \mathbf{B} \times \mathbf{C} & \mathbf{T} \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} \Delta x & 0 & 0 & 0 \\ 0 & \Delta y & 0 & 0 \\ 0 & 0 & \Delta z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}}
\begin{bmatrix} i \\ j \\ k \\ 1 \end{bmatrix}
rotación
traslación
escalamiento
transformación afín
puede añadirse también un shear
De coordenadas intrínsecas a anatómicas
puede añadirse también un shear
\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}=
\underbrace{\begin{bmatrix} \mathbf{B} & \mathbf{C} & \mathbf{B} \times \mathbf{C} & \mathbf{T} \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} \Delta x & 0 & 0 & 0 \\ 0 & \Delta y & 0 & 0 \\ 0 & 0 & \Delta z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}}
\begin{bmatrix} i \\ j \\ k \\ 1 \end{bmatrix}
rotación
traslación
escalamiento
transformación afín
De coordenadas intrínsecas a anatómicas
\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}=
\begin{bmatrix} \mathbf{B} & \mathbf{C} & \mathbf{B} \times \mathbf{C} & \mathbf{T} \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} \Delta x & 0 & 0 & 0 \\ 0 & \Delta y & 0 & 0 \\ 0 & 0 & \Delta z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} i \\ j \\ k \\ 1 \end{bmatrix}
{^A}\hat{\mathbf{i}}
{^A}\hat{\mathbf{j}}
De coordenadas intrínsecas a anatómicas
\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}=
\begin{bmatrix} \mathbf{B} & \mathbf{C} & \mathbf{B} \times \mathbf{C} & \mathbf{T} \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} \Delta x & 0 & 0 & 0 \\ 0 & \Delta y & 0 & 0 \\ 0 & 0 & \Delta z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} i \\ j \\ k \\ 1 \end{bmatrix}
debe calcularse para DICOM aunque puede extraerse directamente en NifTI
De coordenadas intrínsecas a anatómicas
\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}=
\begin{bmatrix} \mathbf{B} & \mathbf{C} & \mathbf{B} \times \mathbf{C} & \mathbf{T} \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} \Delta x & 0 & 0 & 0 \\ 0 & \Delta y & 0 & 0 \\ 0 & 0 & \Delta z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} i \\ j \\ k \\ 1 \end{bmatrix}
{^A}\hat{\mathbf{o}}_S
De coordenadas intrínsecas a anatómicas
\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}=
\begin{bmatrix} \mathbf{B} & \mathbf{C} & \mathbf{B} \times \mathbf{C} & \mathbf{T} \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} \Delta x & 0 & 0 & 0 \\ 0 & \Delta y & 0 & 0 \\ 0 & 0 & \Delta z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} i \\ j \\ k \\ 1 \end{bmatrix}
De coordenadas intrínsecas a anatómicas
\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}=
\begin{bmatrix} \mathbf{B} & \mathbf{C} & \mathbf{B} \times \mathbf{C} & \mathbf{T} \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} \Delta x & 0 & 0 & 0 \\ 0 & \Delta y & 0 & 0 \\ 0 & 0 & \Delta z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} i \\ j \\ k \\ 1 \end{bmatrix}
De coordenadas intrínsecas a anatómicas
\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}=
\begin{bmatrix} \mathbf{B} & \mathbf{C} & \mathbf{B} \times \mathbf{C} & \mathbf{T} \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} \Delta x & 0 & 0 & 0 \\ 0 & \Delta y & 0 & 0 \\ 0 & 0 & \Delta z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} i \\ j \\ k \\ 1 \end{bmatrix}
ya con esto extraemos información anatómica de los voxeles y vemos la posibilidad de enlazarla con sistemas de navegación y/o robóticos
Anclando a sistemas de navegación
{^A}\tilde{\mathbf{p}}=\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}
{^N}\tilde{\mathbf{p}}={^N}\mathbf{T}_W {^W}\mathbf{T}_A{^A}\tilde{\mathbf{p}}
\{N\}
Anclando a sistemas de navegación
{^A}\tilde{\mathbf{p}}=\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}
{^N}\tilde{\mathbf{p}}={^N}\mathbf{T}_W {^W}\mathbf{T}_A{^A}\tilde{\mathbf{p}}
\{N\}
{^N}\mathbf{T}_A
Anclando a sistemas de navegación
{^A}\tilde{\mathbf{p}}=\begin{bmatrix} L \\ P \\ S \\ 1 \end{bmatrix}
{^N}\tilde{\mathbf{p}}={^N}\mathbf{T}_W {^W}\mathbf{T}_A{^A}\tilde{\mathbf{p}}
¿Cómo puede encontrarse esto? mediante un proceso de registro (rígido) empleando algún tipo de puntos característicos como:
- anatomical landmarks
- fiducial markers
{^N}\mathbf{T}_A
\{N\}
Registro
Registro
Anatomical landmarks
Fiducial markers (genéricos)
Fiducial markers (médicos)
Fiducial markers (médicos)
BE3027 - Lecture 12 (2024)
By Miguel Enrique Zea Arenales
