Introduction to computing with Message Passing Interface (MPI)

Oslo - 18/9 2024

 

Professor Mikael Mortensen

Department of Mathematics

University of Oslo

Why MPI?

The only way to simulate extremely large models that can capture extremely complex real-life physics!

Shaheen II - 196,000 cores

What is MPI?

MPI defines a standard interface for communication between processors.

A single MPI parallel program is executed on several processors simultaneously. Each process is assigned different jobs within the same program.

There are several competing implementations of MPI

OpenMPI, MPICH, IntelMPI, ...

The processors do not share the same memory (distributed memory).

MPI basics

communicator1 

Communicators are defined for groups of processes that have the ability to communicate with one another

communicator2 

No communication across

COMM_WORLD

COMM_WORLD

The COMM_WORLD communicator is designed to communicate between all processors

Communicator rank

COMM_WORLD

Each processor in a communicator group has a unique rank​ 

rank 4

rank 0

rank 1

rank 2

rank 3

rank 5

Rank is local to communicator

communicator1 

communicator2 

No communication across

rank 0

rank 1

rank 0

rank 3

rank 2

rank 1

The Communicators job is to send and receive information between ranks

x=10
x=?

For example - a program computes a variable x on rank 0 and sends the result to rank 1

rank 0

rank 1

comm.send(x, dest=1)

x = comm.recv(source=0)

comm

MPI is implemented in C with bindings in many languages

Hello world! Fortran90

program hello_world

  ! Include the MPI library definitons:
  include 'mpif.h'

  integer numtasks, rank, ierr, rc, len, i

  ! Initialize the MPI environment
  call MPI_INIT(ierr)

  ! Get the number of processors
  call MPI_COMM_SIZE(MPI_COMM_WORLD, numtasks, ierr)

  ! Get the rank of the process
  call MPI_COMM_RANK(MPI_COMM_WORLD, rank, ierr)

  print "('Hello World! from rank ',I3,' of ',I3,' processors')",&
       rank, numtasks

  ! Finalize the MPI environment
  call MPI_FINALIZE(ierr)

end program hello_world

helloworld.f90:

>>> mpif90 helloworld.f90 -o helloworld
>>> mpirun -np 4 helloworld
Hello world! from rank 3 of 4 processors
Hello world! from rank 1 of 4 processors
Hello world! from rank 2 of 4 processors
Hello world! from rank 0 of 4 processors

Compile and run

Hello world! C++

#include <mpi.h>

int main(int argc, char** argv) {
    // Initialize the MPI environment
    MPI_Init(NULL, NULL);

    // Get the number of processes
    int world_size;
    MPI_Comm_size(MPI_COMM_WORLD, &world_size);

    // Get the rank of the process
    int world_rank;
    MPI_Comm_rank(MPI_COMM_WORLD, &world_rank);

    printf("Hello world! from rank %d"
           " out of %d processors\n",
           world_rank, world_size);

    // Finalize the MPI environment.
    MPI_Finalize();
}

helloworld.cpp:

>>> mpic++ -o helloworldcpp helloworld.cpp 
>>> mpirun -np 4 helloworldcpp 
Hello world! from rank 1 out of 4 processors
Hello world! from rank 3 out of 4 processors
Hello world! from rank 0 out of 4 processors
Hello world! from rank 2 out of 4 processors

Compile and run

Compiler wrappers

  • There are no direct MPI compilers
  • MPI compiler wrappers add the appropriate compiler and linker flags and call the compiler and linker

C                      -   mpicc                                  -   gcc

C++                  -   mpic++, mpicxx, mpiCC   -  g++

Fortran90       -   mpif90                                -  gfortran

Fortran77       -   mpif77                                -  gfortran

mpirun to execute the parallel program

>>> mpirun -np 4 helloworldcpp 
>>> mpic++ -o helloworldcpp helloworld.cpp

Hello world!

Python (mpi4py)

from mpi4py import MPI
comm = MPI.COMM_WORLD
print("Hello world! from", comm.Get_rank(), "of", comm.Get_size(), "processors")
>>> mpirun -np 4 python helloworld.py
Hello world! from rank 3 of 4 processors
Hello world! from rank 1 of 4 processors
Hello world! from rank 2 of 4 processors
Hello world! from rank 0 of 4 processors

Python script helloworld.py:

Run in a terminal (no compilation):

Python

  • Free Open Source
  • The worlds most popular language
  • Scripting language, similar syntax to MATLAB
  • Complete language. Used extensively by systems and web developers.
  • Very high level of abstraction.
  • Truly simple interfaces to a range of toolboxes (batteries included)
    • MPI
    • LAPACK, BLAS,  FFTW 

mpi4py

mpi4py (https://bitbucket.org/mpi4py) implements Python interfaces to almost the entire MPI

MPI through mpi4py is as fast as pure C

Very high level of abstraction makes it ideal for learning basic MPI:-)

Point to point communication

  • Send
  • Recv
  • Sendrecv

Sending and receiving

from mpi4py import MPI
comm = MPI.COMM_WORLD
assert comm.Get_size() == 2        # Check that only 2 cpus are used

rank = comm.Get_rank()
sendmessage = "from " + str(rank)  # Create a unique message

# Send and receive messages
comm.send(sendmessage, dest=(rank+1)%2)   # % is the modulo operator
rcvmessage = comm.recv(source=(rank+1)%2)

print("Rank", rank, "received the message '", rcvmessage, "'")
>>> mpirun -np 2 python ping.py
Rank 1 received the message ' from 0 '
Rank 0 received the message ' from 1 '

Script "ping.py":

Run script with 2 processors:

The most fundamental part of MPI is the Sending and Receiving of messages (data)

 

Example:

Rank 0 sends the string "from 0" to rank 1

Rank 1 sends the string "from 1" to rank 0

At the same time

 

Rank 1 receives the string "from 0" from rank 0

Rank 0 receives the string "from 1" from rank 1

Send, Recv arrays

Alternatively send and receive a data array of some size

from mpi4py import MPI
comm = MPI.COMM_WORLD
assert comm.Get_size() == 2
import numpy as np   # numpy module for doing math with arrays in Python
import sys           # sys module used here for handling input parameter

rank = comm.Get_rank()
N = eval(sys.argv[-1])         # Get the last argument in the call to program
sendarray = np.random.random(N)# Create N random floats
recvarray = np.zeros(N)
comm.Send(sendarray, dest=(rank+1)%2)    # Large S in Send for numpy arrays
comm.Recv(recvarray, source=(rank+1)%2)  # Large R in Recv for numpy arrays

print("Rank", rank, "sent the array    ", sendarray)
print("Rank", rank, "received the array", recvarray)
>>> mpirun -np 2 python ping_array.py 4
Rank 0 sent the array     [ 0.44237578  0.31677064  0.01413777  0.71446391]
Rank 1 sent the array     [ 0.45921672  0.44309542  0.47930141  0.20993437]
Rank 1 received the array [ 0.44237578  0.31677064  0.01413777  0.71446391]
Rank 0 received the array [ 0.45921672  0.44309542  0.47930141  0.20993437]

Script "ping_array.py":

Run script with 2 processors and N=4:

x = [0.5466, 0.1023, 0.3456, 8.3456]

Send, Recv 2D arrays

Alternatively send and receive a multi-dimensional data array

from mpi4py import MPI
comm = MPI.COMM_WORLD
assert comm.Get_size() == 2
import numpy as np
import sys

rank = comm.Get_rank()
N = eval(sys.argv[-2])   # Get the two commandline arguments
M = eval(sys.argv[-1])
sendarray = np.random.random((N, M))   # Create 2D array of random floats
recvarray = np.zeros((N, M))
comm.Send(sendarray, dest=(rank+1)%2)  # Same call as for 1D arrays!
comm.Recv(recvarray, source=(rank+1)%2)

print("Rank", rank, "sent the array    ", sendarray)
print("Rank", rank, "received the array", recvarray)
>>> mpirun -np 2 python ping_array.py 2 2
Rank 1 sent the array     [[ 0.13015624  0.83936722]
 [ 0.20446479  0.73219369]]
Rank 0 sent the array     [[ 0.0959189   0.29652745]
 [ 0.96000297  0.97902768]]
Rank 1 received the array [[ 0.0959189   0.29652745]
 [ 0.96000297  0.97902768]]
Rank 0 received the array [[ 0.13015624  0.83936722]
 [ 0.20446479  0.73219369]]

Script "ping_array2D.py":

Run script with 2 processors and N=2, M=2:

x = [[0.5466, 0.1023], [0.3456, 8.3456]]

Ping Pong

Rank 0

Rank 1

count

Two players ranked as number 0 and 1

  • Rank 0 counts 1 and sends the ball to rank 1
  • Rank 1 counts 2 and sends the ball to rank 0
  • Rank 0 counts 3 and sends the ball to rank 1
  • Rank 1 counts 4 and sends the ball to rank 0
  • Rank 0 counts 5 and sends the ball to rank 1
  • Rank 1 misses!

Ping Pong

mpirun -np 2 python pingpong.py
Rank 0 counts 1 and sends the ball to rank 1
Rank 1 counts 2 and sends the ball to rank 0
Rank 0 counts 3 and sends the ball to rank 1
Rank 1 counts 4 and sends the ball to rank 0
Rank 0 counts 5 and sends the ball to rank 1
Rank 1 misses!
from mpi4py import MPI
comm = MPI.COMM_WORLD
assert comm.Get_size() == 2

rank = comm.Get_rank()
count = 0
while count < 5:    
    if rank == count%2:
        count += 1
        comm.send(count, dest=(rank+1)%2)
        print("Rank", rank, "counts", count, "and sends the ball to rank", (rank+1)%2)
        
    elif rank == (count+1)%2:
        count = comm.recv(source=(rank+1)%2)
    comm.barrier()
if rank == 1: print("Rank 1 misses!")

pingpong.py

Execute program simultaneously on 2 processors

mpirun -np 2 python pingpong.py

Collective operations

  • Broadcast
  • Reduce
  • Scatter
  • Gather
  • Allgather
  • Alltoall

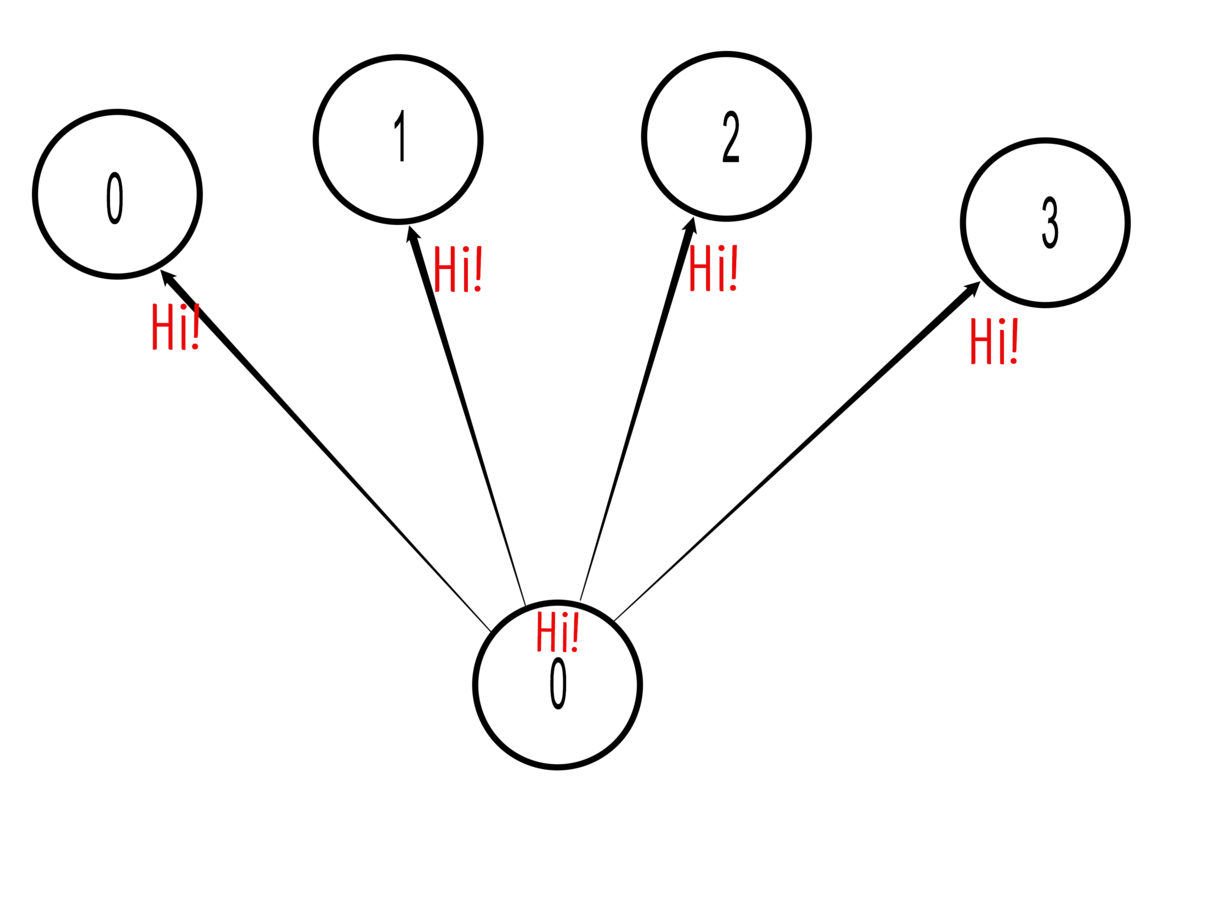
Broadcast

During a broadcast, one process sends the same data to all processes in a communicator. 

from mpi4py import MPI
comm = MPI.COMM_WORLD

rank = comm.Get_rank()
message = None
if rank == 0:
    message = "Hi!"

message = comm.bcast(message, root=0)

if rank > 0:
    print("Rank 0 says", message, "to rank", rank)

>>> mpirun -np 4 python bcast.py 
Rank 0 says Hi! to rank 1
Rank 0 says Hi! to rank 2
Rank 0 says Hi! to rank 3

bcast.py

>>> mpirun -np 4 python bcast.py

Example:

Rank 0 sends the string "Hi!" to all processes

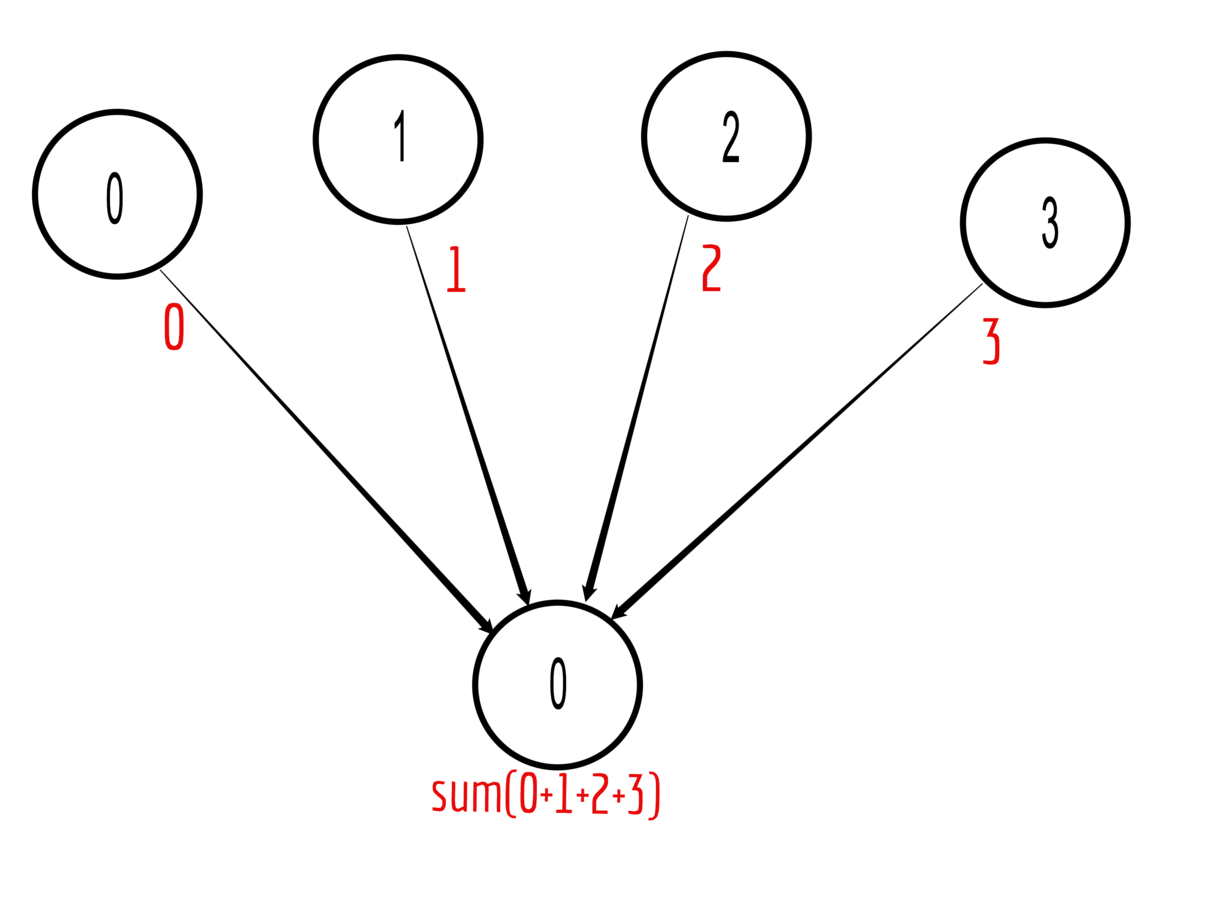
Reduce

 Data reduction by reducing a set of numbers into a smaller set of numbers via a function

 

from mpi4py import MPI
comm = MPI.COMM_WORLD

rank = comm.Get_rank()
data = rank
data = comm.reduce(data, op=MPI.SUM, root=0) # MPI.PROD, MPI.MAX, MPI.MIN, ...

print("On rank", rank,"data =", data)
>>> mpirun -np 4 python reduce.py 
On rank 2 data = None
On rank 3 data = None
On rank 1 data = None
On rank 0 data = 6

reduce.py

>>> mpirun -np 4 python reduce.py

Example:

Set variable data equal to rank on all processes and reduce on rank 0 with sum

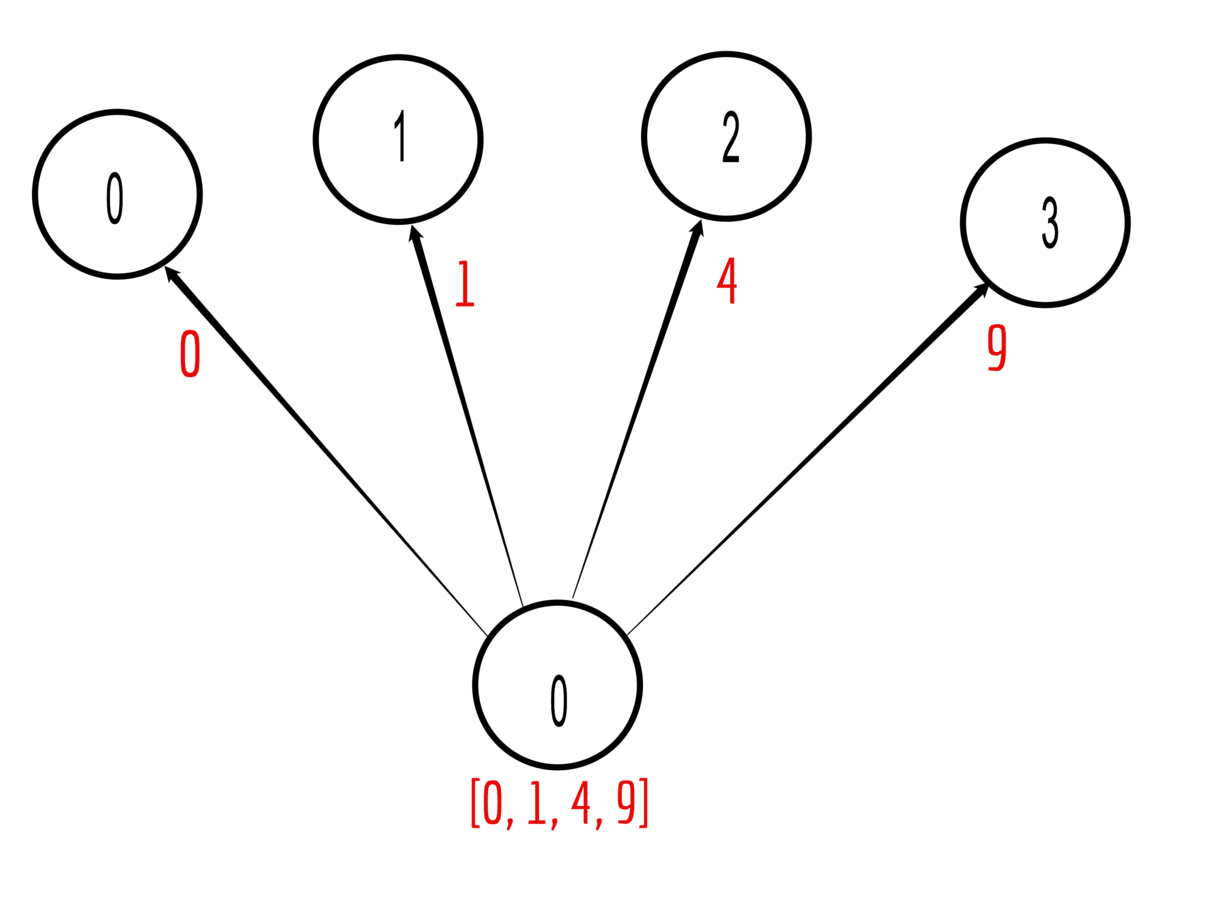
Scatter

One process sends different data to all the ranks

mpirun -np 4 python scatter.py 
Rank 0 data = 0
Rank 1 data = 1
Rank 2 data = 4
Rank 3 data = 9


from mpi4py import MPI
comm = MPI.COMM_WORLD

rank = comm.Get_rank()
data = None
if rank == 0:
    data = [0, 1, 4, 9]
    
data = comm.scatter(data, root=0)

print("Rank", rank, "data =", data)

scatter.py

Example with 4 ranks: 

set data = [0, 1, 4, 9] on rank 0

Send data[i] to rank i, for i = 0, 1, 2, 3

mpirun -np 4 python scatter.py

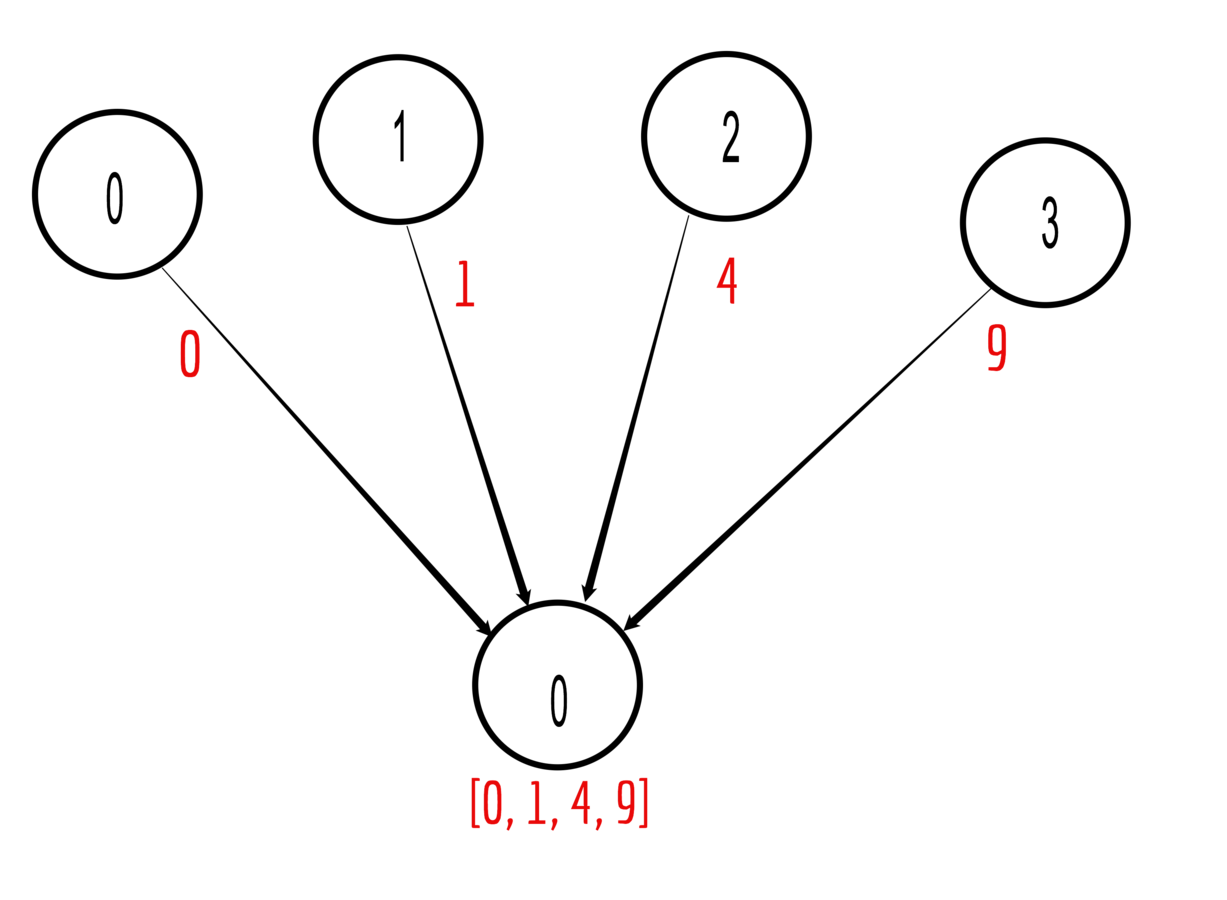
Gather

Gather is the inverse of scatter

Gather data from all processors on one designated rank

>>> mpirun -np 4 python gather.py 
On rank 1 data = None
On rank 2 data = None
On rank 3 data = None
On rank 0 data = [0, 1, 4, 9]

from mpi4py import MPI
comm = MPI.COMM_WORLD

rank = comm.Get_rank()
data = rank**2
data = comm.gather(data, root=0)

print("On rank", rank,"data =", data)

gather.py

>>> mpirun -np 4 python gather.py

Example with 4 ranks:

Set data = rank^2 on all ranks

Gather on rank = 0

Allgather

Gather data from all processors (like normal gather), but broadcast result to all ranks

>>> mpirun -np 4 python allgather.py 
On rank 0 data = [0, 1, 4, 9]
On rank 1 data = [0, 1, 4, 9]
On rank 2 data = [0, 1, 4, 9]
On rank 3 data = [0, 1, 4, 9]


from mpi4py import MPI
comm = MPI.COMM_WORLD

rank = comm.Get_rank()
data = rank**2
data = comm.allgather(data)

print("On rank", rank, "data =", data)

allgather.py

Alltoall

All ranks sends and receives data to and from all other ranks in communicator

>>> mpirun -np 4 python alltoall.py 
On rank 0 data = [0, 0, 0, 0]
On rank 1 data = [1, 1, 1, 1]
On rank 2 data = [2, 2, 2, 2]
On rank 3 data = [3, 3, 3, 3]


from mpi4py import MPI
comm = MPI.COMM_WORLD

rank = comm.Get_rank()
data = range(comm.Get_size())  # [0, 1, 2, ..., size]
data = comm.alltoall(data)

print("On rank", rank,"data =", data)

alltoall.py

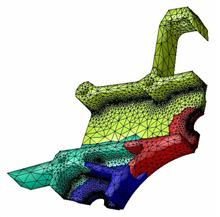
Scientific applications

How is MPI used in scientific computing?

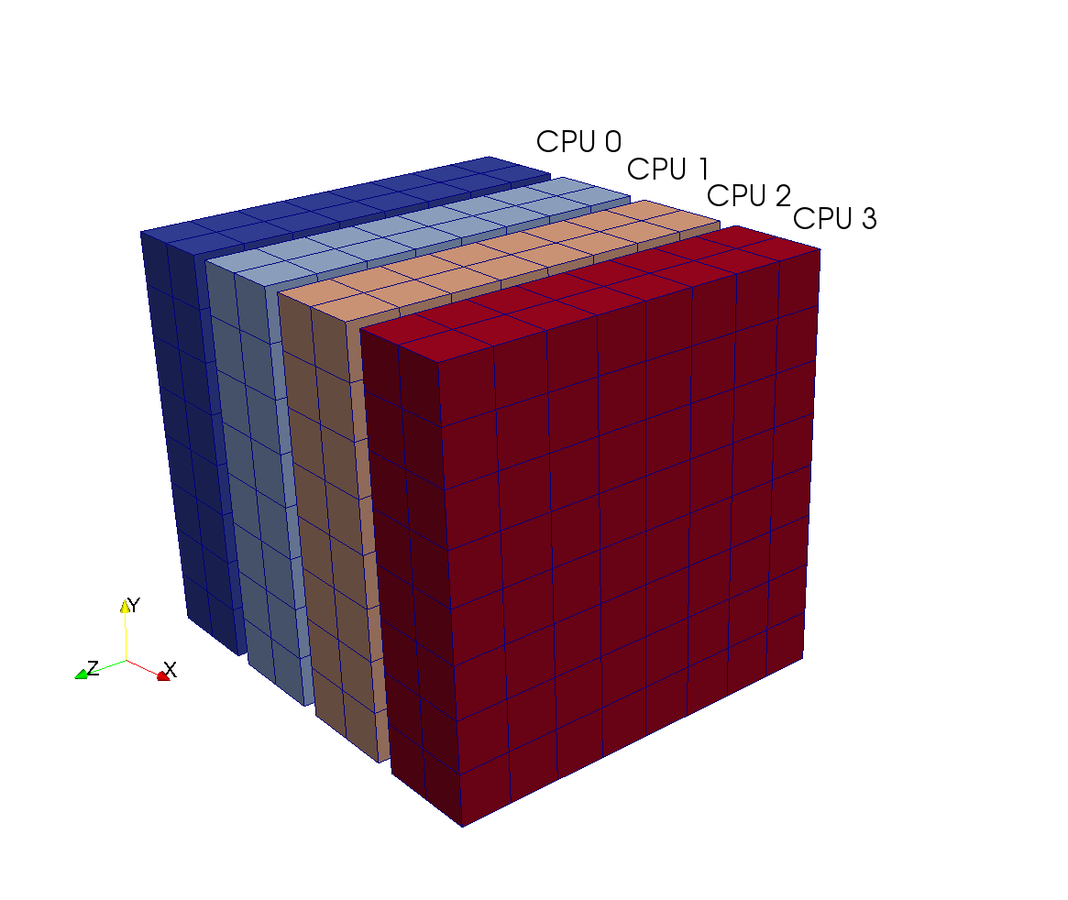
  • A large global mesh is distributed amongst processors 
  • As much work as possible done locally.
  • Boundary values communicated to neighbouring processes. 
  • Linear algebra often outsourced

Worked example

Trapezoidal integration

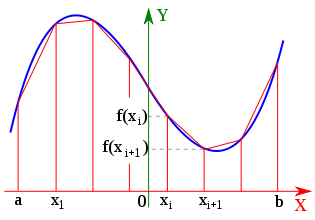
  • Use MPI and create a program to integrate any function        using the trapezoidal rule
  • Verify with exact solution using Python module sympy
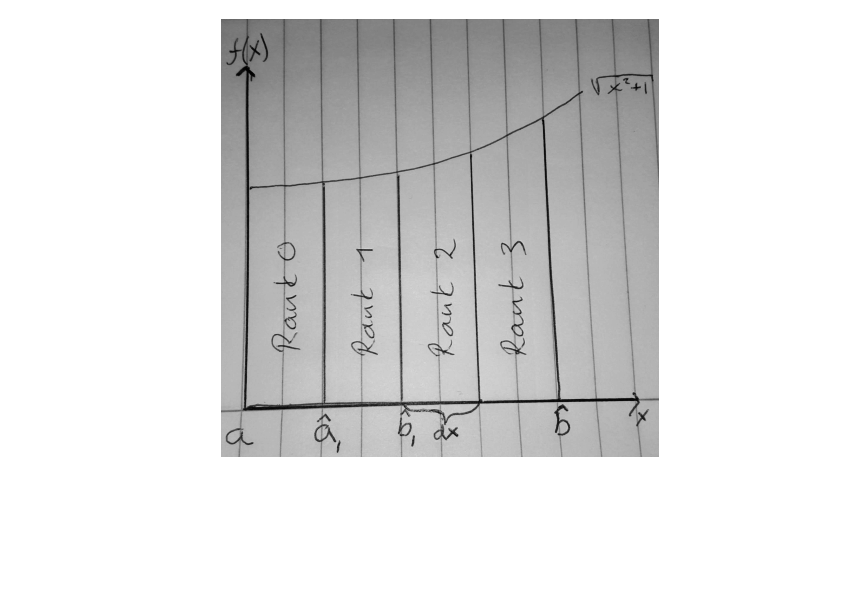
I = \int_{a}^{b}f(x)\, dx \approx \frac{b-a}{N}\left[\frac{1}{2}\left(f(a)+f(b)\right)+\displaystyle{\sum_{i=1}^{N-1}f(x_i)}\right]
f(x)

Step 1

Mesh decomposition

Divide the interval between processors

dx = \frac{b-a}{\text{Num. proc.}}
\hat{a}_{\text{rank}} = \text{rank}\cdot dx
\hat{b}_{\text{rank}} = (\text{rank}+1)\cdot dx
N = \text{Number of subdivisions within each domain}
rank = comm.Get_rank()
size = comm.Get_size()
a = 0.0
b = 1.0
N = eval(sys.argv[-1]) # Number of subdivisions for each rank
dx = (b-a)/size
a_hat, b_hat = rank*dx, (rank+1)*dx
xj = np.linspace(a_hat, b_hat, N+1)   # Mesh in rank's subdivision

Step 2

Define function

import numpy as np

def f(x):
    return np.sqrt(x**2+1)     # Regular Python function

f = lambda x: np.sqrt(x**2+1)  # Lambda function

import sympy
x = sympy.Symbol('x') 
f = sympy.sqrt(x**2+1)         # Symbolic function (for exact integration)

There are many ways of defining a function in Python:

f(x) = \sqrt{x^2+1}

Choose function

Step 3

Compute the integral

\hat{I}_{j} = \frac{\hat{b}_j-\hat{a}_j}{N}\left[\frac{1}{2}\left(f(\hat{a}_j)+f(\hat{b}_j)\right)+\sum_{i=1}^{N-1}f(x_i)\right]

For each rank j compute

fj = [f(y) for y in xj]  # or [f.subs(x, y) for y in xj] for sympy function
Ij = (b_hat-a_hat)/float(N)*(0.5*(fj[0]+fj[-1])+sum(fj[1:-1]))

I = comm.reduce(Ij)      # Sum all contributions on rank 0

Compute total integral using MPI reduce function

Trapezoidal integration

of sympy function through commandline

from mpi4py import MPI
comm = MPI.COMM_WORLD
import sys
import numpy as np
import sympy

x = sympy.Symbol("x")
f = eval(sys.argv[-1])
rank = comm.Get_rank()
size = comm.Get_size()
a, b = 0.0, 1.0
N = eval(sys.argv[-2]) # Number of subdivisions for each rank
dx = (b-a)/size
a_hat = rank*dx
b_hat = (rank+1)*dx
xj = np.linspace(a_hat, b_hat, N+1)
fj = [f.subs(x, y) for y in xj]
Ij = (b_hat-a_hat)/float(N)*(0.5*(fj[0]+fj[-1])+sum(fj[1:-1]))
I = comm.reduce(Ij)
if rank == 0:
    print("Integral of f(x) from ", a, "to", b, "is ≈", I)
    print("Exact                               = ", f.integrate((x, (a, b))).evalf())


    
>>> mpirun -np 8 python trapz.py 10 'sympy.sqrt(x**2+1)'
Integral of f(x) from  0.0 to 1.0 is ≈ 1.14780278183385
Exact                                = 1.14779357469632

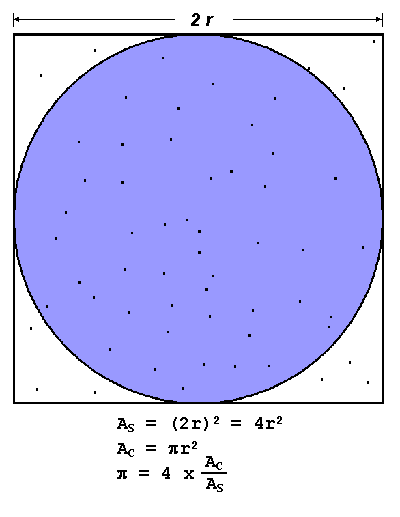
Exercise 1

Compute the value of

Use MPI programming and Monte Carlo integration to compute the value of 

How many particles are required for 4 digits accuracy?

\pi
\pi

Exercise 2

Integration using Simpson's rule

  • Modify trapz.py to use the composite Simpson's rule instead of the trapezoidal rule.
  • Modify the code to work with any interval size of the decomposed mesh, not just uniform.
I = \int_{a}^{b}f(x)\, dx \approx \frac{b-a}{3N}\left[f(a)+f(b)+\displaystyle{\sum_{i=1}^{N/2}4f(x_{2i-1})}+2\displaystyle{\sum_{i=1}^{N/2-1}f(x_{2i})}\right]

Exercise 3

Ring send and receive

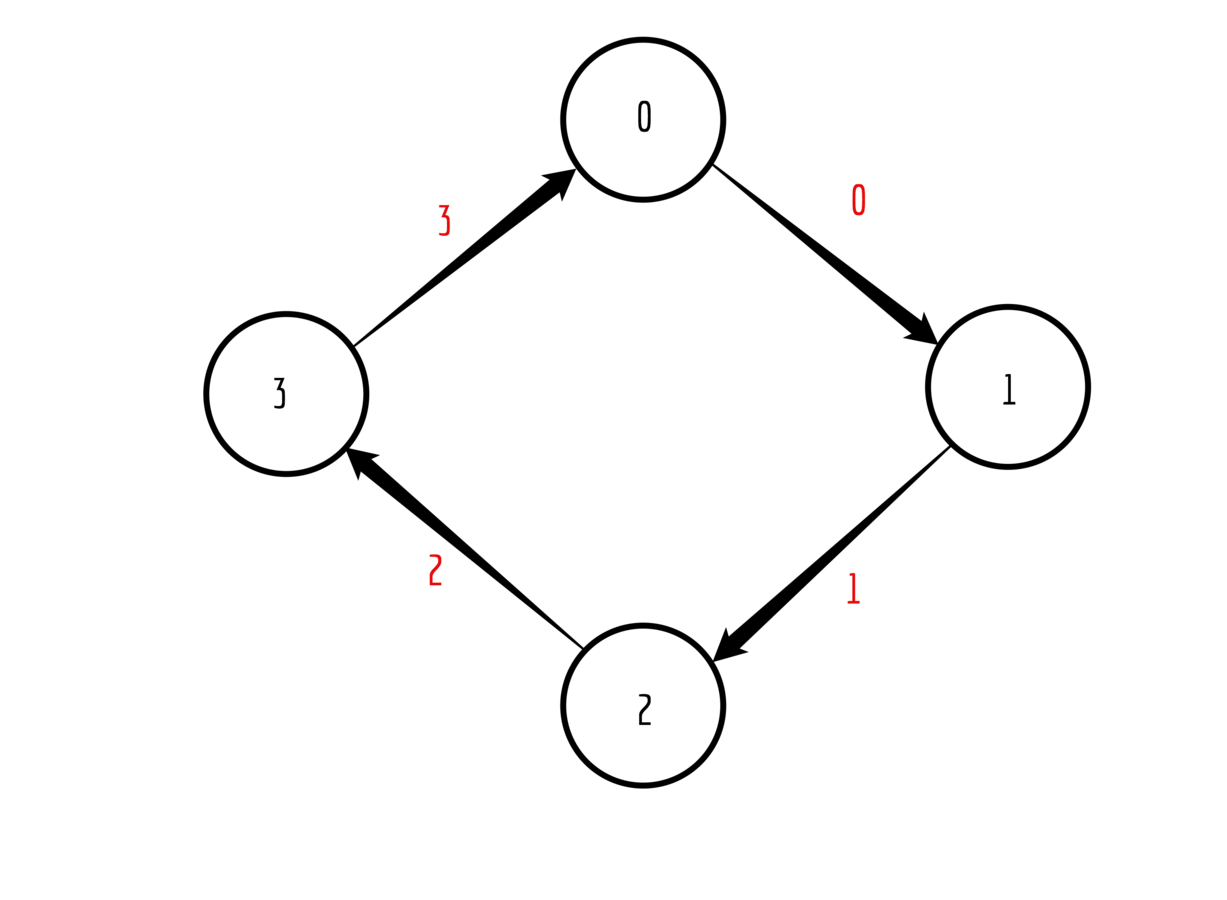
Each rank starts by sending the value of its rank to the closest neighbour on the right, i.e., (rank+1)%(number of ranks)

Pass on the received value to the next neighbour

Keep track of the sum of all received values

Stop when receiving your own rank

Print out the accumulated sum

First step

Exercise 4

Matrix vector product

  • Given a global matrix A[N, N] and a vector x[N]
  • Compute the matrix vector product through MPI by distributing the matrix such that its local size on each rank is A[Np, N], where Np = N/(Number of ranks)
  • Verify the result by comparing to a serial code
Ax=b

mpi-intro

By Mikael Mortensen

Made with Slides.com

mpi-intro

  • 872

More from Mikael Mortensen