CS6015: Linear Algebra and Random Processes
Lecture 19: Algebraic and Geometric Multiplicity, Schur's theorem, Spectral theorem for Symmetric matrices, Trace of a matrix
Learning Objectives
What is algebraic and geometric multiplicity of an eigenvalue?
When would the two be equal?
What does Schur's theorem say about factorisation of a matrix?
What is Spectral theorem for symmetric matrices?
What is the trace of a matrix and how is it related to eigenvalues?
The Eigenstory
real
imaginary
distinct
repeating
\(A^\top\)
\(A^{-1}\)
\(AB\)
\(A^\top A\)
(basis)
powers of A
steady state
PCA
optimisation
diagonalisation
\(A+B\)
\(U\)
\(R\)
\(A^2\)
\(A + kI\)
How to compute eigenvalues?
What are the possible values?
What are the eigenvalues of some special matrices ?
What is the relation between the eigenvalues of related matrices?
What do eigen values reveal about a matrix?
What are some applications in which eigenvalues play an important role?
Identity
Projection
Reflection
Markov
Rotation
Singular
Orthogonal
Rank one
Symmetric
Permutation
det(A - \lambda I) = 0
trace
determinant
invertibility
rank
nullspace
columnspace
(Markov matrices)
(positive semidefinite matrices)
positive pivots
(independent eigenvectors)
(orthogonal eigenvectors)
... ...
(symmetric)
(where are we?)
(characteristic equation)
(desirable)
HW5
distinct values
independent eigenvectors
\(\implies\)
The bigger picture
* more than 1 value can repeat - e.g. in a projection matrix both the eigenvalues 1 and 0 may repeat
(questions)
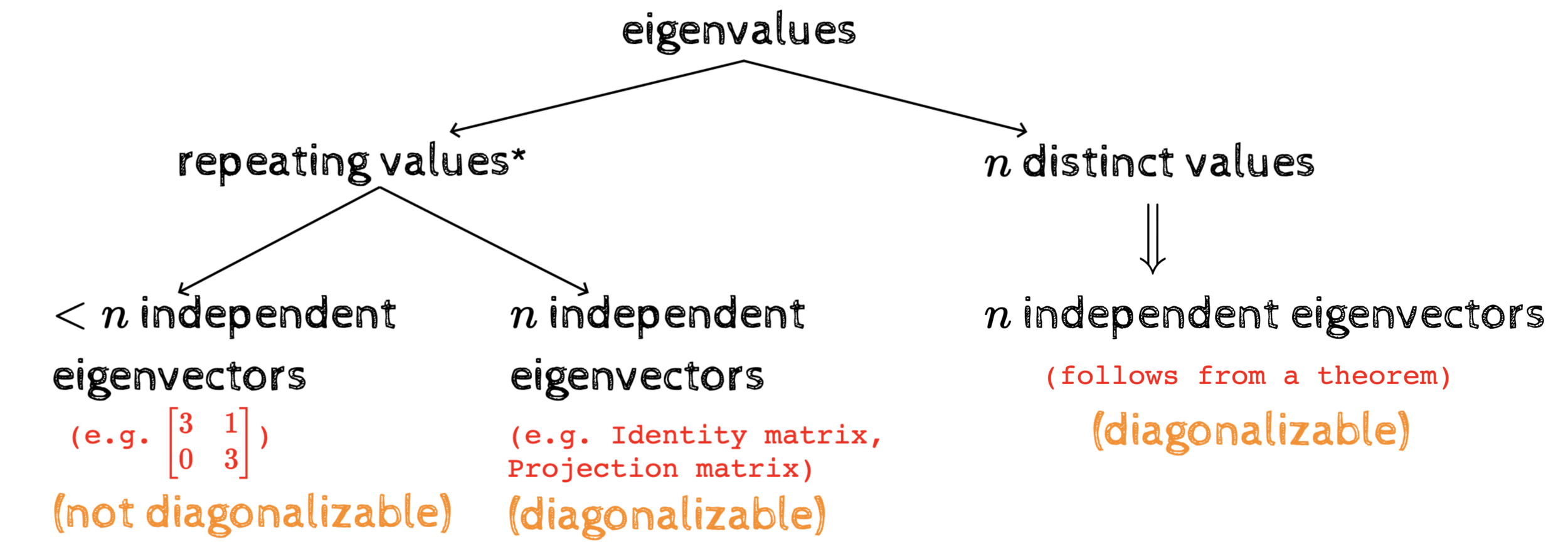
What do we mean by saying that a matrix is diagonalizable?
Why do we care about diagonalizability?
What is the condition under which we will have \(n\) independent vectors even with repeating eigenvalues?
Multiplicity
For a given eigenvalue \(\lambda\)
Geometric Multiplicity(GM) is the number of independent eigenvectors for \(\lambda\)
Algebraic Multiplicity(AM) is the number of repetitions of \(\lambda\) among the eigenvalues
GM\leq AM
The good case (no repeating eigenvalues)
GM = AM=1~~\forall \lambda
Multiplicity
When would the number of independent eigenvectors be the same as the number of repetitions of \(\lambda\)?

Hint: How do we find the eigenvectors for a given \(\lambda\) ?
By solving \((A - \lambda I)\mathbf{x} = \mathbf{0}\)
\(\therefore\) number of independent eigenvectors = dimension of nullspace
\(\therefore\) GM = dimension of null space of \(A - \lambda I\)
If an eigenvalue repeats \(p\) times and the dimension of the nullspace of \((A-\lambda I)\) is also \(p\) then GM = AM
(i.e. when would GM be equal to AM)
(i.e. by finding vectors in the nullspace of
(i.e.~~if~~rank(A - \lambda I) = n-p)
A - \lambda I)
The bigger picture
* more than 1 value can repeat - e.g. in a projection matrix both the eigenvalues 1 and 0 may repeat

Are there matrices which will always have \(n\) independent eigenvectors (even when one or more eigenvalues are repeating) ?
Yes, symmetric matrices
Real Symmetric matrices
we like real numbers as opposed to imaginary numbers
Properties
\(n\) real eigenvalues
\(n\) orthogonal eigenvectors
*
*
always diagonalisable
*
the best possible basis
S = Q\Lambda Q^{-1} = Q\Lambda Q^{T}
even when there are repeating eigenvalues
(we will prove this soon)
(we will prove this soon)
(all elements are real and the matrix is symmetric)
(we will not prove this completely - not even in HW5 :-))
Real Symmetric matrices
(all elements are real and the matrix is symmetric)
Proof:
Let \(\lambda = a + ib\) be an eigenvalue,
\(\overline{\lambda} = a - ib\)
S\mathbf{x} = \lambda \mathbf{x}
\therefore S\overline{\mathbf{x}} = \overline{\lambda} \overline{\mathbf{x}}
(taking conjugate on both sides, S is real)
\therefore \overline{\mathbf{x}}^\top S = \overline{\mathbf{x}}^\top\overline{\lambda}
(taking transpose on both sides, S is symmetric)
multiply both sides by conjugate of x
multiply both sides by x
\overline{\mathbf{x}}^\top S\mathbf{x} = \overline{\mathbf{x}}^\top \lambda \mathbf{x}
\overline{\mathbf{x}}^\top S\mathbf{x} = \overline{\mathbf{x}}^\top \overline{\lambda} \mathbf{x}
\therefore \lambda \overline{\mathbf{x}}^\top \mathbf{x} = \overline{\lambda} \overline{\mathbf{x}}^\top \mathbf{x}
\therefore \lambda = \overline{\lambda}
\because \overline{\mathbf{x}}^\top \mathbf{x} \neq 0
\therefore a+ib = a-ib
\implies b = 0
Hence~proved!
Where did we use the property that the matrix is real symmetric?
Theorem: All the eigenvalues of a real symmetric matrix are real
Real Symmetric matrices
(all elements are real and the matrix is symmetric)
Theorem: Eigenvectors of a real symmetric matrix corresponding to different eigenvalues are orthogonal
Proof:
Let~~S\mathbf{x} = \lambda_1 \mathbf{x}~~and~~S\mathbf{y} = \lambda_2 \mathbf{y}~~and~~\lambda_1 \neq \lambda_2
\mathbf{x}^\top\lambda_1\mathbf{y}
= (\lambda_1\mathbf{x})^\top\mathbf{y}
= (S\mathbf{x})^\top\mathbf{y}
= \mathbf{x}^\top S^\top\mathbf{y}
= \mathbf{x}^\top S\mathbf{y}
= \mathbf{x}^\top \lambda_2\mathbf{y}
\therefore \lambda_1\mathbf{x}^\top\mathbf{y}=\lambda_2\mathbf{x}^\top\mathbf{y}
\implies \lambda_1=\lambda_2~~or~~\mathbf{x}^\top\mathbf{y}=0
But~~\lambda_1\neq\lambda_2
\therefore~~\mathbf{x}^\top\mathbf{y}=0
(Hence proved)
Real Symmetric matrices
Proved
Properties
\(n\) real eigenvalues
What about the case when some eigenvalues repeat?
*
*
always diagonalisable
*
Proved for the case when eigenvalues are not repeating
(all elements are real and the matrix is symmetric)
Follows from Theorem 2 when the eigenvalues are not repeating
\(n\) orthogonal eigenvectors
(see next few slides)
S = Q\Lambda Q^{-1} = Q\Lambda Q^{T}
Schur's Theorem
Theorem : If \(A\) is a square matrix with real eigenvalues, then there is an orthogonal matrix \(Q\) and an upper triangular matrix \(T\) such that,
\(A = QTQ^\top\)
Corollary : If \(A\) is a square symmetric matrix with real eigenvalues, then there is an orthogonal matrix \(Q\) and a diagonal matrix \(T\) such that,
\(A = QTQ^\top\)
Proof:
A = QTQ^\top
A^\top = (Q T Q^\top)^\top = Q T^\top Q^\top
But~~A = A^\top
\therefore QTQ^\top = QT^\top Q^\top
\therefore T = T^\top
upper triang.
lower triang.
Hence, T must be diagonal
(we will not prove this)
from Schur's Theorem
symmetric
Spectral Theorem
Theorem : If \(A\) is a real square symmetric matrix , then
every eigenvalue of \(A\) is a real number
eigenvectors corresponding to different eigenvalues are orthogonal
\(A\) can be diagonalised as \(Q D Q^\top\)
(orthogonal matrix of eigenvectors of A)
(diagonal matrix of eigenvalues of A)
*
*
*
Proved
Proved
therefore q_i's must be eigenvectors and d_i's must be eigenvalues
From~~corollary~~of~~Schur's~~theorem
Proof (of 3rd part):
A = QTQ^\top
\therefore AQ = QT
T is diagonal
\therefore A
\begin{bmatrix}
\uparrow&\uparrow&\uparrow \\
q_1&\dots&q_n \\
\downarrow&\downarrow&\downarrow \\
\end{bmatrix}
=
\begin{bmatrix}
\uparrow&\uparrow&\uparrow \\
q_1&\dots&q_n \\
\downarrow&\downarrow&\downarrow \\
\end{bmatrix}
\begin{bmatrix}
d_1&\dots&0 \\
0&\dots&0 \\
0&\dots&d_n \\
\end{bmatrix}
\therefore \begin{bmatrix}
\uparrow&\uparrow&\uparrow \\
Aq_1&\dots&Aq_n \\
\downarrow&\downarrow&\downarrow \\
\end{bmatrix}
=
\begin{bmatrix}
\uparrow&\uparrow&\uparrow \\
d_1q_1&\dots&d_nq_n \\
\downarrow&\downarrow&\downarrow \\
\end{bmatrix}
(even if there are repeating eigenvalues)
even if there are repeating eigenvalues
Spectral Theorem
(informal conclusion)
Real symmetric square matrices are the best possible matrices
*
always diagonalisable
*
with real eigenvalues
*
with orthogonal eigenbasis
we love diagonalizability
we love real numbers
we love orthogonal basis
One last property about symmetric matrices
sorry for squeezing it in here
number of positive pivots = number of positive eigenvalues
thus connecting the two halves of the course
(HW5)
The Eigenstory
real
imaginary
distinct
repeating
\(A^\top\)
\(A^{-1}\)
\(AB\)
\(A^\top A\)
(basis)
powers of A
steady state
PCA
optimisation
diagonalisation
\(A+B\)
\(U\)
\(R\)
\(A^2\)
\(A + kI\)
How to compute eigenvalues?
What are the possible values?
What are the eigenvalues of some special matrices ?
What is the relation between the eigenvalues of related matrices?
What do eigen values reveal about a matrix?
What are some applications in which eigenvalues play an important role?
Identity
Projection
Reflection
Markov
Rotation
Singular
Orthogonal
Rank one
Symmetric
Permutation
det(A - \lambda I) = 0
trace
determinant
invertibility
rank
nullspace
columnspace
(Markov matrices)
(positive semidefinite matrices)
positive pivots
(independent eigenvectors)
(orthogonal eigenvectors)
... ...
(symmetric)
(where are we?)
(characteristic equation)
(desirable)
HW5
distinct values
independent eigenvectors
\(\implies\)
Two properties

The trace of a matrix is the sum of the diagonal elements of the matrix
tr(A) = \sum_{i=1}^n a_{ii}
defined only for square matrices
If \(\lambda_1, \lambda_2, \dots, \lambda_n\) are the eigenvalues of a matrix \(A\) then
tr(A) = \sum_{i=1}^n \lambda_{i}
det(A) = \prod_{i=1}^n \lambda_{i}
(Proof in HW5)
(Proof in HW5)
The Eigenstory
real
imaginary
distinct
repeating
\(A^\top\)
\(A^{-1}\)
\(AB\)
\(A^\top A\)
(basis)
powers of A
steady state
PCA
optimisation
diagonalisation
\(A+B\)
\(U\)
\(R\)
\(A^2\)
\(A + kI\)
How to compute eigenvalues?
What are the possible values?
What are the eigenvalues of some special matrices ?
What is the relation between the eigenvalues of related matrices?
What do eigen values reveal about a matrix?
What are some applications in which eigenvalues play an important role?
Identity
Projection
Reflection
Markov
Rotation
Singular
Orthogonal
Rank one
Symmetric
Permutation
det(A - \lambda I) = 0
trace
determinant
invertibility
rank
nullspace
columnspace
(Markov matrices)
(positive definite matrices)
positive pivots
(independent eigenvectors)
(orthogonal eigenvectors)
... ...
(symmetric)
(where are we?)
(characteristic equation)
(desirable)
HW5
distinct values
independent eigenvectors
\(\implies\)
Positive Definite Matrices
pivots, eigenvalues, determinants, \( x^\top Ax\) > 0
write quadratic equation for 2 6 2 7
geometry by replacing the 7 by 18, 20
Learning Objectives
What is algebraic and geometric multiplicity of an eigenvalue?
When would the two be equal?
What does Schur's theorem say about factorisation of a matrix?
What is Spectral theorem for symmetric matrices?
What is the trace of a matrix and how is it related to eigenvalues?
CS6015: Lecture 19
By Mitesh Khapra
CS6015: Lecture 19
Lecture 19: Algebraic and Geometric Multiplicity, Schur's theorem, Spectral theorem for Symmetric matrices, Trace of a matrix
- 2,600



